Материальная точка массой m движется в плоскости oxy согласно уравнениям (7 видео)

Точки в декартовой системе отсчёта

Условие задачи.

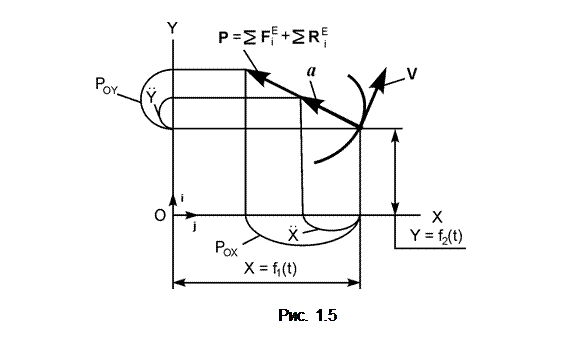
Под действием горизонтальной силы F₁ движение материальной точки массой m = 8 кг происходит по гладкой горизонтальной плоскости OXY согласно уравнениям X = 0,05·t 3 , Y = 0,3·t 2 . Определить модуль равнодействующей приложенных к точке сил в момент времени t₁ = 4 с (рис. 1.5).

Решение.

1. Выбираем систему отсчёта ОXY.

2. Изобразим точку на траектории её движения в произвольный момент времени. Согласно известным положениям кинематики скорость V точки направлена по касательной к траектории движения, а её ускорение а направлено в сторону вогнутости траектории движения.

3. Так как начальные условия движения точки не заданы, то на рис. 1.5 они не показаны.

4. Согласно условию задачи к точке приложены активные силы F₁ и G. Так как поверхность, по которой перемещается точка, гладкая, на точку действует только нормальная реакция N. Основное уравнение динамики для рассматриваемой задачи имеет вид m·a = ΣF_i Е + ΣR_i Е = G + F₁ + N. Поскольку рис. 1.5 приведён в ортогональной проекции, то сила тяжести G и нормальная реакция N не

Материальная точка массой m движется в плоскости oxy согласно уравнениям

показаны.

5. Запишем дифференциальные уравнения движения точки.

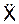
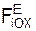
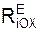
m· = Σ + Σ = F₁_OX = Р_OX; (1)

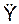
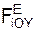
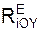
m· = Σ + Σ = F₁_OY = Р_OY; (2)

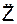
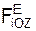
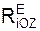
m· = Σ + Σ = F₁_OZ = P_OZ. (3)

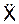
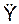
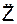
6. По заданным уравнениям движения X = 0,05·t 3 , Y = 0,3·t 2 определим проекции , , ускорения точки на координатные оси.

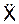
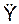
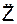
7. Найденные значения , , подставим в уравнения (1), (2), (3).

8. Определим модуль Р равнодействующей активных сил и реакций внешних связей.

= .

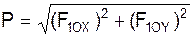
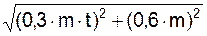
9. Вычислим значения F₁_OX, F₁_OY, P для момента времени t₁= 4 c.

= 10,733 H.

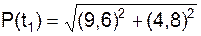
10. Определим направляющие косинусы и углы, составленные направлениями координатных осей и силой.

cos(P(t₁), i) = F_1OX(t₁)/P(t₁) = 9,6/10,733 = 0,894; α = 26,563 о ;

cos(P(t₁), j) = F_1OY(t₁)/P(t₁) = 4,8/10,733 = 0,447; β = 63,434 о .

11. Определим координаты точки на траектории её движения в момент времени t₁, и полученную информацию отобразим на рис. 1.6: X(t₁) = 0,05·4 3 = 3,2 м; Y(t₁) = 0,3·4 2 = 2,4 м.

Видео:Материальная точка. Система отсчета | Физика 9 класс #1 | ИнфоурокСкачать

Определение сил по заданному движению

ДИНАМИКА ТОЧКИ

Определение сил по заданному движению

13.1.1Точка массой m=4 кгдвижется по горизонтальной прямой с ускорениемa=0,3t. Определить модуль силы, действующей на точку в направлении ее движения в момент времени t=3c. (3.6) Решение:Зная массу и ее ускорение, можно определить действующую на точку силу, в момент времени t=3c , ускорение будет

тогда

13.1.2Ускорение движения точки массой m=27кгпо прямой задано графиком функции a=а(t). Определить модуль равнодействующей сил, приложенных к точке в момент времени t=5c. (4,05) Решение:Из графика видно что при t=5c , ускорение а=0,15м/с 2 , тогда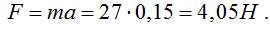

13.1.3 Деталь массой m=0,5кг скользит вниз по лотку. Под каким углом к горизонтальной плоскости должен располагаться лоток, для того чтобы деталь двигалась с ускорением а=2 м/с 2 ? Угол выразить в градусах. (11,8) Решение:Деталь движется под силой тяжести G=mg, сила под которой она движется по

лотку с некоторым углом а,

13.1.4Точка массой m=14кгдвижется по горизонтальной оси Ох с ускорениема_х.=lnt Определить модуль силы, действующей на точку в направлении движения в момент времени t=5c. (22,5) Решение:

13.1.5Трактор, двигаясь с ускорением а=1м/с 2 по горизонтальному участку пути, перемещает нагруженные сани массой 600кг. Определить силу тяги на крюке, если коэффициент трения скольжения саней f=0,04. (835) Решение:Необходимая сила тяги на крюке для перемещения саней с заданным ускорением 1м/с 2 :

13.1.6Тело массой m=50 кг, подвешенное на тросе, поднимается вертикально с ускорением а=0,5м/с 2 . Определить силу натяжения троса.(516) Решение:

13.1.7 Скорость движения точки m=24кг по прямой задана графиком функцииv=v(t). Определить модуль равнодействующей сил, действующих на точку. (36) Решение: из графика функции v=v(t) видно, что точка движется равноускоренно с ускорением а=1,5м/с, тогда равнодействующая сил

13.1.8 Материальная точка массой m=12кгдвижется по прямой со скоростьюv=е 0,1t . Определить модуль равнодействующей сил, действующих на точку в момент времени t=50c.(178) Решение:

13.1.9 Определить модуль равнодействующей сил, действующих на материльную точку массой m=3кг в момент времени t=6c, если она движется по оси Ох согласно уравнению х=0,04t 3 . (4,32) Решение:Ускорение точки найдем из уравнения движения (вторая производная по времени):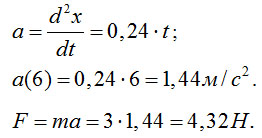

13.1.10 Материальная точка массой 1,4кг движется прямолинейно по законух=6t 2 +6t+3 . Определить модуль равнодействующей сил, приложенных к точке.(16,8) Решение:

Определение сил по заданному движению

Видео:13.1. Определение сил по заданному движениюСкачать

Курсовая работа. Выполнение

Контрольные вопросы и задания к теме 2.

При выполнении каких условий точка будет двигаться под действием силы в одной плоскости OXY

1. Если сила лежит в этой плоскости.

2. Если и лежат в этой плоскости.

3. Если лежит в этой плоскости.

№12. Точка массы m движется в плоскости по криволинейной траектории под действием силы F. Дифференцированные уравнения ее движения имеют вид:

Укажите неверный ответ.

№13. Материальная точка массы m движется по окружности радиуса a согласно уравнению S=bt . Определить силу, вызывающую это движение.

3. Нет верного решения.

№14. Груз А опускается вниз по негладкой наклонной плоскости, рас положенной под углом a к горизонту (рис. 11), двигаясь согласно уравнению x=bgt2; b = const. Определить Fmp.

1. Fmp = P(sin> a — 2b).

2. Fmp = f N = fPcos> a .

3. Нет верного ответа. Рис. 11

15. Определить натяжение нити математического маятника

длины l и веса P, если качания маятника > j = j 0sinkt, где

j — угол отклонения маятника от вертикали; j 0 и к, — постоянные величины.

№16. Материальная точка весом 10 кг движется по окружности радиуса R = 100 м в горизонтальной плоскости под действием переменной силы закону S = 0,1t3 см.

Определить силу, действующую на точку, когда скорость точки V = 30 м/с (g = 10/с2).

№17. Точка массой m движется из состояния покоя по окружности радиуса R с постоянным касательным ускорением a> t . Определить силу,

действующую на точку в момент, когда она пройдет расстояние S = R .

3. F = Fn = 2 ma t .

№18. Точка массой m движется согласно уравнениям: x = 2sin3t; y = 2cos3t. Определить силу, действующую на точку. Которая задача динамики здесь сформулирована?

1. Вторая. F = 18 т.

4. Первая. F = 18 т.

№19. Дифференциальные уравнения движения материальной точки в неподвижной системе координат имеют вид:

Укажите неверный ответ.

№20. Дифференциальные уравнения движения материальной точки в естественном системе координат имеют вид:

Укажите неверный ответ.

Тема 3. Прямолинейное движение точки. Динамика относительного движения

Рассмотрим решение второй основной задачи динамики для случая прямолинейного движения. Пусть некоторая точка M массы m движется под действием силы прямолинейно (рис. 12). Считаем, что прямая, по которой движется точка M, ось x, положительное направление оси — в сторону движения точки. Запишем дифференциальное уравнение для данной точки: , но X=F, .

Окончательный вид его: Рис. 12

Сила, действующая на точку, может быть постоянной или переменной.

1. > = const. F = const, то =const, движение происходит с постоянным ускорением, т.е. оно является равнопеременным. Закон его известен из кинематики .

2. > const. Рассмотрим три случая.

1). F = F(t) — сила, являющаяся функцией времени. Найдем закон движения точки, т.е. решаем вторую основную задачу динамики. Для решения необходимо составить дифференциальное уравнение

Начальные условия (x0, V0) t0 = 0. Имеем дифференциальное уравнение с разделяющимися переменными, разделим их и проинтегрируем:

Закон изменения скорости >

Найдем скорость, дальше заменим > , еще раз интегрируя, находим x.

Закон движения точки > (2)

Лекция 7. Синтез многозвенных зубчатых механизмов.

Вопросы, рассматриваемые на лекции. Синтез многозвенных зубчатых передач с неподвижными осями. Планетарные коробки скоростей. Синтез многозвенных зубчатых передач с подвижными осями.

Некоторые основные понятия. Для получения больших передаточных отношений применяют соединения зубчатых колес.

Последовательное соединение. На промежуточных валах имеется по два колеса (рис.17). Общее передаточное отношение iобщ последовательного соединения равно произведению отдельных зубчатых пар, то есть

Через числа зубьев колес общее передаточное отношение последовательного соединения выражается следующим образом:

Здесь в числителе — произведение чисел зубьев ведомых колес, а в знаменателе– ведущих колес. Знак общего передаточного отношения зависит от числа k пар внешнего зацепления: при четном числе k — «плюс», при нечетном числе k — «минус».

Рядовое соединение колес. На промежуточных валах расположено по одному колесу (рис.18). Общее передаточное отношение рядового соединения равно:

то есть передаточное отношение равно обратному отношению чисел зубьев крайних колес и не зависит от числа зубьев промежуточных колес, которые называются паразитными.

Рядовое соединение применяют для соединения валов, отстоящих на большое расстояние друг от друга, либо для изменения направления вращения ведомого вала.

Для ступенчатого изменения передаточного отношения применяют коробки скоростей (рис.19). При перемещении блока шестерен, посаженного на скользящую шпонку, вдоль вала I в зацепление вступают попарно колеса z1-z2, z3-z4 или z5-z6. В зависимости от этого могут быть получены следующие передаточные отношения:

Величина общего передаточного отношения может быть определена опытным путем. Для этого мелом наносят отметки на ведущий и ведомый валы, а также на корпус. Повернув ведущий вал на несколько оборотов, подсчитывают число оборотов ведомого вала. Например, если при повороте ведущего вала на 6 оборотов, ведомый вал сделал 7 оборотов, то общее передаточное отношение .