Материальная точка массой 2 кг двигалась под действием силы согласно уравнению (5 видео)

Содержание

Материальная точка массой 2 кг двигалась под действием силы согласно уравнению
Материальная точка массой т=2 кг движется под действием некоторой силы F согласно уравнению ,v = А + Bt+Cr + Dt где С=1 м/с2 , £>=-0,2 м/с3.
Материальная точка массой 2 кг двигалась под действием силы согласно уравнению
🔍 Видео

Видео:Физика. Динамика. Тело на наклонной плоскости 2Скачать

Материальная точка массой 2 кг двигалась под действием силы согласно уравнению

Материальная точка массой 2 кг движется вдоль горизонтальной оси Ox под действием горизонтальной силы F. В начальный момент времени тело покоилось. График зависимости силы F от времени t изображён на рисунке. Чему равен импульс материальной точки в конце второй секунды? (Ответ дайте в килограммах на метр в секунду.)

Если сила постоянна, то импульс, переданный телу за некоторый промежуток времени, равен произведению этой силы на время действия этой силы. Из рисунка видим, что в конце второй секунды импульс материальной точки равен:

Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Материальная точка массой т=2 кг движется под действием некоторой силы F согласно уравнению ,v = А + Bt+Cr + Dt где С=1 м/с2 , £>=-0,2 м/с3.

🎓 Заказ №: 21911

⟾ Тип работы: Задача

📕 Предмет: Физика

✅ Статус: Выполнен (Проверен преподавателем)

🔥 Цена: 149 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

Материальная точка массой т=2 кг движется под действием некоторой силы F согласно уравнению ,v = А + Bt+Cr + Dt где С=1 м/с2 , £>=-0,2 м/с3 . Найти значения этой силы в моменты времени /1=2 с и 12=5 с. В какой момент времени сила равна нулю?

Решение Уравнение, описывающее зависимость скорости от времени, найдем, продифференцировав координату по времени: (1) Функциональную зависимость ускорения от времени найдем, используя определение ускорения, как второй производной от координаты по времени: (2) Подставим в (2) выражение (1): (3)

=-0,2 м/с3 . Найти значения этой силы в моменты времени /1=2 с и 12=5 с. В какой момент времени сила равна нулю? » /> =-0,2 м/с3 . Найти значения этой силы в моменты времени /1=2 с и 12=5 с. В какой момент времени сила равна нулю? » />

Научись сам решать задачи изучив физику на этой странице:

Решение задач по физике

Услуги:

Заказать физику
Помощь по физике

Готовые задачи по физике которые сегодня купили:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:№ 301-400 - Физика 10-11 класс РымкевичСкачать

Материальная точка массой 2 кг двигалась под действием силы согласно уравнению

Глава 17. Принцип Даламбера.

17.1. Метод кинетостатики для материальной точки.

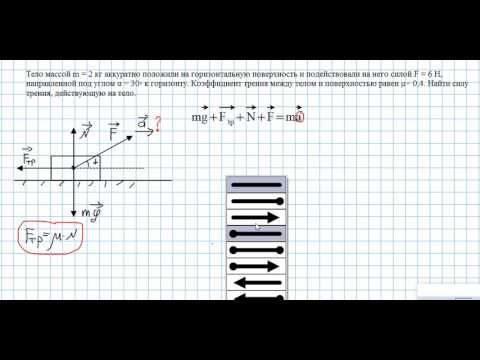
17.1.1. Материальная точка массой m = 2 кг скользит по негладкой горизонтальной плоскости под действием силы F = 10Н, составляющей угол α = 30° с горизонтальной плоскостью. Определить ускорение материальной точки, если коэффициент трения скольжения f = 0,1. (Ответ 3,60)

17.1.2. Груз массой m = 60 кг подвешен на нити, которая наматывается на барабан, вращающийся согласно уравнению φ = 0,6t 2 . Определить натяжение каната, если радиус r = 0,4 м. (Ответ 617)

17.1.3. Материальная точка массой m = 0,6 кг колеблется в вертикальном направлении согласно закону х = 25 + 3 sin 20t, где х — в см. Определить модуль реакции пружины в момент времени t = 2 с. (Ответ 11,3)

17.1.4. Материальная точка массой m = 1 кг совершает затухающие колебания в вертикальном направлении. В момент времени, когда ускорение точки а = 14 м/с 2 и скорость ее v = 2 м/с, определить реакцию пружины, если сила сопротивления демпфера R = -0,1 v. (Ответ 23,6)

17.1.5. Материальная точка массой m = 12 кг подвешена на двух одинаковых пружинах. На нее действует сила F = 20Н. Определить модуль усилия в одной пружине, если в данном положении материальная точка имеет ускорение а = 3 м/с 2 . (Ответ 174)

17.1.6. Автомобиль, масса которого m = 8·10 3 кг, двигаясь по мосту, тормозит с замедлением а = 6 м/с 2 . Принимая автомобиль за материальную точку, определить в кН модуль горизонтальной нагрузки на опору О моста. (Ответ 48)

17.1.7. Горизонтальная платформа 1 вибростенда совершает в вертикальном направлении гармонические колебания с амплитудой 8 мм и частотой 8 Гц. К платформе прикреплен датчик 2 массой 50 г. Определить максимальное значение силы, которая стремится оторвать датчик от платформы. (Ответ 0,520)

17.1.8. Горизонтальная виброплатформа 1, на которой лежит деталь 2, совершает гармонические колебания в вертикальном направлении с амплитудой 1 мм. Частоту колебаний можно менять, сохраняя ту же амплитуду. Определить максимальную частоту, при которой деталь 2 еще не отрывается от платформы 1. (Ответ 15,8)

17.1.9. Вибролоток 1 совершает гармонические колебания по горизонтальной направляющей с амплитудой 0,981 см. Определить максимальное значение угловой частоты колебаний в рад/с, при которой деталь 2 еще не скользит по лотку. Коэффициент трения скольжения детали по лотку f = 0,1. (Ответ 10)

17.1.10. Определить, с каким ускорением а надо двигать клин 1 по горизонтальной направляющей, чтобы материальная точка 2 не скользила по наклонной поверхности клина.
(Ответ 5,66)

17.1.11. Какой наибольшей скорости может достичь материальная точка массой m = 1 кг, которая опускается по наклонной плоскости с углом наклона α = 30 o , если на нее действует суммарная сила сопротивления движению R = 0,11 v, где v — скорость движения, м/с?
(Ответ 44,6)

17.1.12. Материальная точка массой m = 10 кг движется по окружности радиуса r = 3 м согласно закону движения s = 4t 3 . Определить модуль силы инерции материальной точки в момент времени t = 1с. (Ответ 537)

17.1.13. Материальная точка М движется в вертикальной плоскости по внутренней поверхности цилиндра радиуса r = 9,81 м. Определить минимальную скорость v точки, при которой в указанном положении не произойдет ее отрыва от цилиндра. (Ответ 9,81)

17.1.14. Материальная точка массой m = 0,1 кг скользит но негладкой, вертикально расположенной направляющей радиуса r = 0,4 м. В самом нижнем положении скорость точки v = 4 м/с, а касательное ускорение а_τ = 7 м/с 2 . Определить мгновенное значение силы F, если коэффициент трения f = 0,1. (Ответ 1,20)

17.1.15. Материальная точка М массой m = 2 кг удерживается в равновесии двумя наклонными нитями. Определить натяжение одной нити в момент времени непосредственно после обрыва второй. (Ответ 9,81)

17.1.16. Луна движется вокруг Земли на расстоянии 384 400 км от центра Земли с орбитальной скоростью 163 м/с. Масса Луны равна 7,35 · 10 22 кг. Определить силу, с которой Земля притягивает Луну, считая Луну материальной точкой. (Ответ 5,08 · 10 18 )

17.1.17. По негладкой направляющей радиуса r = 0,5 м, расположенной в горизонтальной плоскости, скользит материальная точка массой m = 1,5 кг с постоянной скоростью v = 2 м/с под действием силы F. Определить модуль силы F, если коэффициент трения скольжения f = 0,15. (Ответ 2,85)

17.1.18. Определить в градусах угол а отклонения стержня AM с точечной массой М на конце от вертикальной оси вращения, если вал ОА совместно со стержнем AM равномерно вращается с угловой скоростью ω = 4,47 рад/с, а длина l = 0,981 м. Массой стержня AM пренебречь. (Ответ 60)

17.1.19. Чаша вращается с постоянной угловой скоростью ω вокруг вертикальной оси. Определить наибольшее значение угловой скорости, при которой материальная точка М еще не начнет подниматься но стенке чаши. Коэффициент трения скольжения между точкой М и стенкой чаши f = 0,1, радиус r = 0,2 м. (Ответ 7,74)

17.1.20. Автомашина движется по прямому участку пути со скоростью v = 140 км/ч. К ободу диска колеса на расстоянии r = 20 см прикреплен балансировочный груз массой m = 80 г. Определить максимальную силу давления груза на обод колеса. Радиус колеса R = 35 см. Колебания колеса не учитывать. (Ответ 198)

17.1.21. Материальная точка массой m = 2 кг скользит со скоростью v по негладкой горизонтальной плоскости под действием силы F = 15Н, расположенной в той же плоскости. Определить модуль силы инерции материальной точки, если коэффициент трения скольжения равен 0,3. (Ответ 13,1)

17.1.22. Материальная точка М массой m = 4 кг движется согласно закону s = 0,5 t 2 + 0,5 sin 4t. В момент времени t = 5 с радиус кривизны траектории точки ρ = 4 м. Определить в этот момент времени модуль силы инерции материальной точки. (Ответ 42,2)

17.1.23. Манипулятор перемещает деталь массой m = 1 кг, которую можно считать материальной точкой, согласно уравнениям движения х = 6t, у = 5t 2 , z = 4t 2 . Определить модуль силы, с которой деталь действует на схват манипулятора. (Ответ 20,4)

17.1.24. Трубка вращается вокруг вертикальной оси с постоянной угловой скоростью ω = 1 рад/с под действием пары сил с моментом М. Внутри трубки движется материальная точка массой m = 0,1 кг. В момент времени, когда t = 0,2 м и относительная скорость точки v_τ = 2 м/с, определить момент М. (Ответ 0,08)

17.1.25. Трубка вращается с постоянной угловой скоростью ω = 2 рад/с вокруг горизонтальной оси. По трубке движется материальная точка массой m = 0,2 кг с относительным ускорением а_τ = 4 м/с 2 . Определить модуль силы F в момент времени, когда l = 0,2 м, а трубка находится в вертикальной плоскости. (Ответ 2,38)