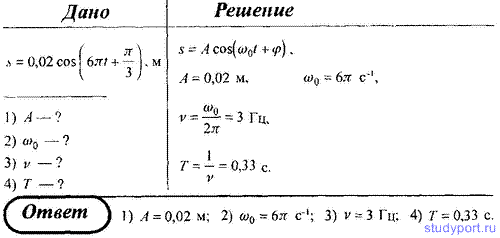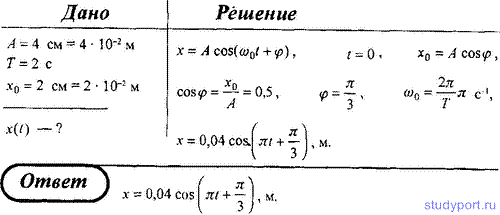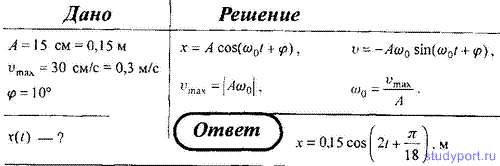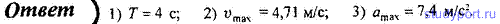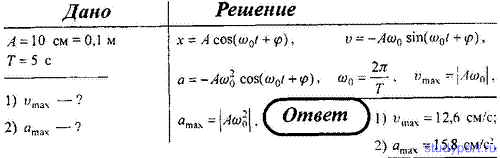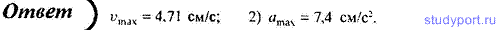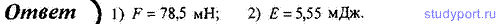Материальная точка колеблется согласно уравнению х 3cos7t амплитуда скорости данной точки равна

4. Колебания и волны

1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x₀ = 2 см.

4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

5. Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки v_max = 30 см/с, начальная фаза φ = 10°.

6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость V_max точки; 3) максимальное ускорение a_max точки.

7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.

9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x₁ = 15 см. При возрастании фазы колебания в два раза смещение x₂ оказалось равным 24 см. Определите амплитуду A колебания.

10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.

11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.

12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х₀ = 5 см, со скоростью v₀ = -15 см/с. Определите амплитуду колебаний.

13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.

14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.

16. Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.

17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω₀t + φ).

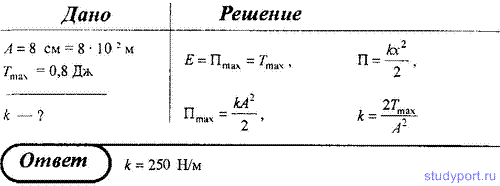
19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия T_max груза составляет 0,8 Дж.

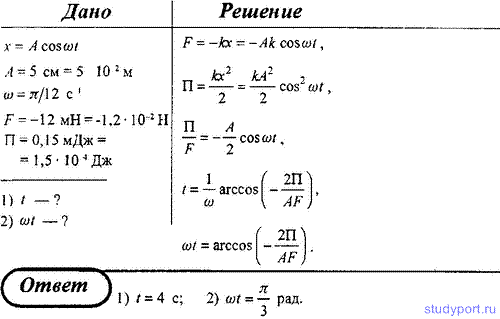
20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с -1 . Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Материальная точка колеблется согласно уравнению x = 3sin(2t + pi / 3)см?

Физика | 10 — 11 классы

Материальная точка колеблется согласно уравнению x = 3sin(2t + pi / 3)см.

Найти маскимальные значения скорости и ускорения точки.

Vm = xm * w = 0, 03 * 2 = 0, 06 м / с

a = Vm * w = 0, 06 * 2 = 0, 12 м / с2.

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Материальная точка массой м колеблется с периодом Т и амплитудой х?

Материальная точка массой м колеблется с периодом Т и амплитудой х.

Полная энергия материальной точки равна.

Видео:Материальная точка. Система отсчета | Физика 9 класс #1 | ИнфоурокСкачать

Две материальные точки движутся с одинаковыми скоростями по окружностям с радиусами и , причем Сравните центростремительные ускорения материальных точек :1?

Две материальные точки движутся с одинаковыми скоростями по окружностям с радиусами и , причем Сравните центростремительные ускорения материальных точек :

Ускорение первой материальной точки в 4 раза больше, чем второй

Ускорение первой материальной точки в 2 раза меньше, чем второй

Ускорение первой материальной точки в 2 раза больше, чем второй.

Видео:Материальная точкаСкачать

Дано уравнение координаты материальной точки x = 15(t + 2) как движется точка?

Дано уравнение координаты материальной точки x = 15(t + 2) как движется точка?

Чему равны скорость и ускорение точки?

Построить графики скорости и ускорения.

Видео:Урок 327. Гармонические колебанияСкачать

Найти моменты времени, в которые скорость и ускорение достигают максимальных значений?

Найти моменты времени, в которые скорость и ускорение достигают максимальных значений.

Движение материальной точки описывается уравнением x = sin(Пи / 3) * t /.

Видео:Выполнялка 53.Гармонические колебания.Скачать

Две материальные точки движутся согласно уравнениям?

Две материальные точки движутся согласно уравнениям.

Видео:Кинематика материальной точки за 20 минут (кратко и доступно) Кинематика точкиСкачать

Найти зависимость скорости от времени, скорость и ускорение точки через 4 секунды после начала движения , если уравнение движения материально точки имеет следующий вид x = 8 + 5t + t ^ 2?

Найти зависимость скорости от времени, скорость и ускорение точки через 4 секунды после начала движения , если уравнение движения материально точки имеет следующий вид x = 8 + 5t + t ^ 2.

Видео:Материальная точка. Система отсчета. Видеоурок по физике 9 классСкачать

Движение материальной точки задано уравнением x = 4t — 0, 05t2 ?

Движение материальной точки задано уравнением x = 4t — 0, 05t2 .

Определить момент времени, в который скорость точки равна нулю.

Найти координаты и ускорение в этот момент.

Видео:Физика 9 класс. §25 Гармонические колебанияСкачать

Материальная точка движется прямолинейно?

Материальная точка движется прямолинейно.

Уравнение движения имеет вид , где A = 3 м / с ; .

Найти скорость v и ускорение точки в моменты времени t1 = 0 и t2 = 3 с.

Каковы средние значения скорости и ускорения за первые 3 с движения?

Видео:Физика Амплитуда колебаний точки струны 1 мм, частота 1 кГц. Какой путь пройдет точка за 0,2 с?Скачать

Материальная точка движется согласно уравнению x(t) = 5 + 10t – –2t2?

Материальная точка движется согласно уравнению x(t) = 5 + 10t – –2t2.

Найти проекции скорости Vx и ускорения ах материальной точки в момент времени t1 = 5 c.

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Скорость движения материальной точки задана уравнением V = 5 + 2t?

Скорость движения материальной точки задана уравнением V = 5 + 2t.

Определить ускорение точки, начальную скорость, построить график скорости.

Написать уравнение движения точки Х = Х(t).

Вы перешли к вопросу Материальная точка колеблется согласно уравнению x = 3sin(2t + pi / 3)см?. Он относится к категории Физика, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Физика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

В вакууме нет сопротивления воздуха, а в воздухе есть, то есть молекула будет затрачивать энергию из — за воздуха. В вакууме такого яления не произойдет.

45 (расстояние) : 3 (время) = 15.

Q = mL + cmt’ = cm(tпл — 30) = 2 * 112000 + 380 * 2 * (420 — 30) = 520400 Дж.

Выражения для силы тяготения имеет вид : F = G * m1 * m2 / r ^ 2, где G — гравитационная постоянная (6, 67 * 10 ^ — 11 м ^ 3 / (кг * с ^ 2)), m1, m2 — массы тел, а r — расстояние между ними. Выражаем отсюда расстояние : r ^ 2 = G * m1 * m2 / F r = √..

Ответа в этой задаче НЕТ! Мы не пойдем искать клад, потому что не знаем, ГДЕ РАСПОЛОЖЕН ЭТО ДУБ.

От график движения двух тел : из графика видно, что точка пересечения : t = 2 ; x = 12. Это время и место встречи. Алгебраически время и место встречи находится так : приравниваем x1 и x2 и решаем уравнение : 20 — 4t = 10 + t ; 20 — 10 = 5t ; t = 2..

Y = 48, 6 mmdndnfnfndndndndndd.

64 это 1 ^ 3, 2 ^ 3, 3 ^ 3, следующее 4 ^ 3 = 64.

Видео:КОЛЕБАНИЯ физика 9 класс решение задачСкачать

Примеры решенных задач по физике -Контрольная 1(гармонические колебания, плоские волны, кольца Ньютона, дифракция, поляризация света)

Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.

Точка совершает гармонические колебания с амплитудой А=10 см и периодом Т=5 с. О п ределите для точки : 1) максимальную скорость, 2) максимальное ускорение.

Дано : A =10 см=0 .1 м

Найти : v max , a max

Уравнение гармонического колебания точки имеет вид :

x = Acos ( ω t + φ ) (1)

Формулу скорости получим, взяв первую производную по времени от смещения :

v= 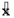=dx/dt=-A ω sin( ω t+ φ )

Максимальная скорость точки равна :

v max =- A ω (2) , где А – амплитуда колебаний ; ω – круговая частота колебаний.

Круговая частота колебаний ω связана с периодом колебаний Т выражением :

С учётом (3) формула (2) примет вид :

v max =-2 π A / T (4)

Ускорение точки найдём, взяв производную по времени от скорости :

a= 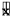=dv/dt=-A ω 2 cos( ω t+ φ )

Максимальное ускорение, равно :

С учётом (3) перепишем формулу (5) в виде :

a max =-4 π 2 A / T 2 (6)

Производя вычисления по формулам (4) и (6), найдём максимальные скорость и ускорение точки.

v max =-2×3.14×0.1/5=-0.13 м/с

a max =-4×3.14 2 ×0.1/5 2 =-0.16 м/с 2

Ответ : v max =-0.13 м/с ; a max =-0.16 м/с 2

Волна с периодом Т=1.2 с и амплитудой колебания А=2 см распространяется со скоростью 15 м/с. Чему равно смещение точки, находящейся на расстоянии 45 м от источника волн в тот момент, когда от начала колебаний источника прошло время t = 4 с ?

Уравнение плоской волны имеет вид :

y ( x , t )= Acos ( ω t — kx ) (1) , где y – смещение точек среды с к о ординатой x в момент времени t ; ω – круговая частота ; k – волновое число.

Волновое число k связано с длиной волны λ выражением :

k =2 π / λ (2) , где λ = vT ; v – скорость распространения колебаний ; T – период колебаний.

Циклическая частота ω связана с периодом Т выражением :

С учётом (2) и (3) уравнение (1) примет вид :

y(x,t)=Acos(2 π t/T-2 π x/(vT))=Acos 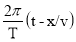(4 )

Вычисления по формуле (4), дают :

y (45 ; 4)=0.02× cos 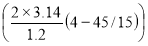=0.01 м=1 см

Ответ : y(45 ; 4)=1 см.

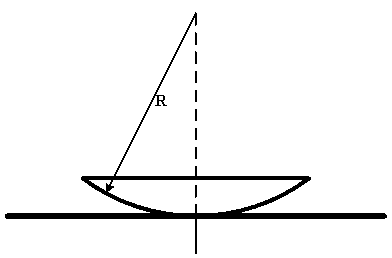
Определить радиус второго темного кольца Ньютона в отраженном свете, если прибор, состоящий из плосковыпуклой линзы с радиусом кривизны 8 м и плоской пластины освещается монохроматическим светом с длиной волны 640 нм.

Дано : λ =64 0 нм= 6.5×10 — 7 м

Радиус темных колец Ньютона в отражённом свете определяется формулой :

r k = 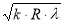(1)

где k – номер кольца ; R – радиус кривизны линзы ; λ – длина волны.

3,2∙10 — 3 м .

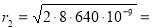
Ответ : r 2 = 3,2∙10 — 3 м .

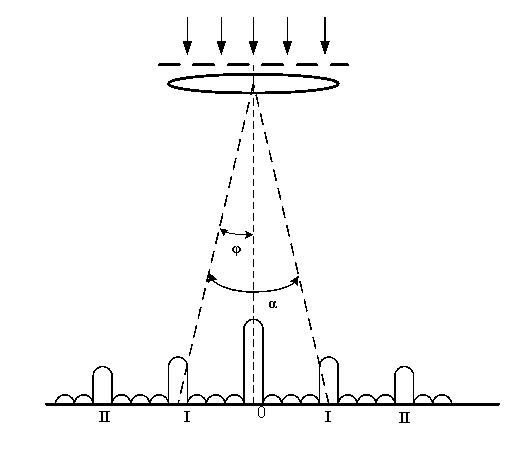
Постоянная дифракционной решётки в n =4 раза больше длины световой волны монохр о ма тического света, нормально падающего на её поверхность. Определить угол α между дв у мя первыми симметричными дифракционными максимумами.

Постоянная дифракционной решётки d , длина волны λ и угол  отклонения лучей соо т ветст вующий К – му дифракционному максимуму, связаны соотношением

dsin  = kλ , или sin  = kλ / d (1)

где к – порядок максимума (в данном случае к=1). Учитывая, что λ/ d =1/ n перепишем форм у лу (1) в виде:

Из рисунка видно, что угол α равен удвоенному углу  . Тогда формула (2) примет вид:

sin ( α /2)= k / n , откуда α=2 arcsin ( k / n )

Подставим в последнюю формулу числовые значения и вычислим:

На сколько процентов уменьшается интенсивность света после прохождения через призму Николя, если потери света составляют 10% ?

Естественный свет, падая на грань призмы Николя, расщепляется вследствие двойного л у чепреломления на два пучка : обыкновенный и необыкновенный. Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного пучка лежит в плоскости чертежа. Плоскость колебаний обыкновенного пучка перпенд и кулярна плоскости чертежа. Обыкновенный пучок (о) вследствие полного отражения от грани AB отбрасывается на зачернённую поверхность призмы и поглощается ею. Необы к новенный пучок (е) проходит через призму. При этом интенсивность света уменьшается вследствие поглощения в веществе николя. Таким образом, интенсивность света, пр о шедшего через призму :

где k = 0.1 – относительная потеря интенсивности света в николе ; I 0 – интенсивность е с тественного света, падающего на николь.

Относительное уменьшение интенсивности света получим, разделив интенсивность I 0 ест е ственного света, падающего на первый николь, на интенсивность I 1 поляризованного св е та :

(1)

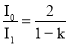
Вычисления по формуле (1) дают :

=2.2

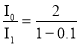
Процентное уменьшение интенсивности :

n % = 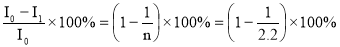=54.5 %

Ответ : при прохождения света через призму интенсивность уменьшится на 54.5%.

Найти длину волны де Бройля для электрона, движущегося по круговой орбите атома водорода, находящегося в основном состоянии.

Длина волны де Бройля λ частицы зависит от её импульса p и определяется формулой :

Импульс частицы можно определить, если известна её скорость v . Связь импульса со скоростью для нерелятивистского (когда v c ) и для релятивистского (когда v ≈ c ) случаев соответственно выражается формулами :

p=m 0 v (2) ; p= 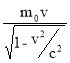(3)

Формула (1) с учётом соотношений (2) и (3) запишется соответственно в нерелятивис т ском и релятивистском случаях :

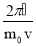
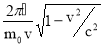
λ = (4) ; λ = (5)

Найдём скорость электрона на круговой орбите атома водорода, находящегося в осно в ном состоянии, из следующих соображений. Согласно теории Бора, радиус r электронной орбиты и скорость v электрона на ней связаны равенством mvr = n ħ . Так как нам требуется скорость электрона на первой орбите, то главное квантовое число n =1 и равенство примет вид :

Откуда скорость электрона :

v = 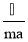(6)

где ħ – постоянная Планка (ħ= 1.05×10 -34 Дж·с) ; m – масса покоя электрона

( m =9.11×10 — 31 кг ) ; a – радиус первой орбиты (а= 5.29×10 — 11 м – Боровский радиус).

Найдём скорость электрона, произведя вычисления по формуле (6) :

v = 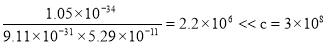м/с

Следовательно , можно применить формулу (4). С учётом (6) формула (4) примет вид :

Вычисления по формуле (7) дают :

λ =2×3.14×5.29×10 -11 =3.3×10 — 10 м

Ответ : λ =3.3×10 — 10 м .=0.33 нм.

Имя файла: physics1.doc

Размер файла: 456.5 Kb

Если закачивание файла не начнется через 10 сек, кликните по этой ссылке

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Уравнение движения точки x=0,05*cos(3*pi*t) (м). Чему равна амплитуда

Видео:Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Условие задачи:

Уравнение движения точки (x = 0,05cos left( right)) (м). Чему равна амплитуда ускорения?

Задача №9.1.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Видео:§1.Физика 9 кл. Материальная точка. Система отсчета.Скачать

Решение задачи:

Чтобы найти уравнение ускорения точки при этих колебаниях, нужно дважды взять производную от данного в условии уравнения колебаний. Сначала возьмем первую производную:

Теперь берем вторую производную:

То есть мы имеем:

[a = – 0,05 cdot 9 cdot cos left( right)]

Понятно, что максимальное по модулю значение ускорения в таком случае равно (оно имеет место, когда косинус по модулю равен 1):

Видео:Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Ответ: 4,44 м/с 2 .

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

🌟 Видео

Якута А. А. - Механика - Гармонические колебания. Собственные затухающие колебанияСкачать

Урок 329. Задачи на гармонические колебания - 1Скачать

График гармонического колебания | Алгебра 10 класс #23 | ИнфоурокСкачать

Поступательное движение. Материальная точкаСкачать