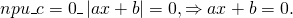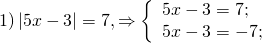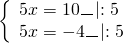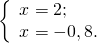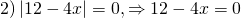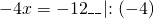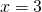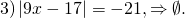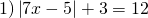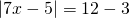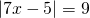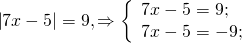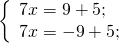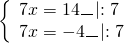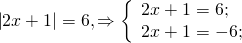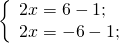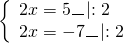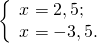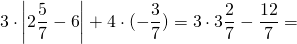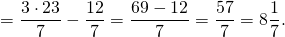план-конспект урока по алгебре (6 класс) по теме
Тип урока: урок обобщения и систематизации предметных знаний.
Цели и задачи урока:
— систематизировать знания учащихся по теме «Решение уравнений с модулем»;
— обеспечить условия для формирования навыков решения уравнений с модулем;
— развивать аналитическое мышление учащихся, внимание;
— развивать коммуникативные качества;
-воспитывать чувство ответственности, товарищества, взаимопонимания, уважительного отношения друг к другу, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цели.
Это третий урок по теме «Модуль числа», по типу — урок обобщения и систематизации предметных знаний, по виду — комбинированный.
Видео:Модуль числа. Практическая часть. 6 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| urok_matematiki_v_6_klasse_reshenie_uravneniy_s_modulem.rar | 2.8 МБ |
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Предварительный просмотр:
МБОУ «Бриентская средняя общеобразовательная школа» Кваркенского района Оренбургской области
Урок математики в 6 классе
Учитель математики высшей категории Бакеева И. Р.
Технологическая карта урока.
Учитель: Бакеева Ирина Ринатовна
Тема урока: Решение уравнений с модулем
Место и роль урока в изучаемой теме: третий урок по теме «Модуль числа», п. 28 учебника Математика, 6 класс. / Н.Я. Виленкин, В.И. Жохов, А.С.Чесноков, С.И. Шварцбурд. / М.: Мнемозина, 2011
Тип урока: урок обобщения и систематизации предметных знаний
Цель урока: систематизировать знания учащихся по изученной теме.
— систематизировать знания учащихся по теме «Решение уравнений с модулем»;
— обеспечить условия для формирования навыков решения уравнений с модулем,
— развивать аналитическое мышление учащихся, внимание;
— развивать коммуникативные качества;
— воспитывать чувство ответственности, товарищества, взаимопонимания, уважительного отношения друг к другу, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цели.
Планируемые результаты : быстрое включение учащихся в деловой ритм и организации внимания у всех учащихся; активная деятельность всего класса в ходе проверки знаний учащихся; активная познавательная деятельность; качество знаний учащихся на последних этапах обучения; умение выделять существенные признаки уравнений с модулем; правильное выполнение д/з всеми учащимися.
По источникам знаний: словесные, наглядные;
По степени взаимодействия учитель-ученик: эвристическая беседа;
Относительно дидактических задач: подготовка к восприятию;
Относительно характера познавательной деятельности: репродуктивный, частично-поисковый.
Формы организации учебной деятельности : индивидуальная, фронтальная работа, групповая деятельность.
Педагогические технологии: здоровьесберегающие технологии, информационно — коммуникативные технологии, технология деятельностного метода, технология уровневой дифференциации, педагогические технологии по выявлению и поддержке одарённых детей.
Межпредметные связи: биология и музыка.
Оборудование : Математика. 6 класс: учебник для общеобразовательных учреждений / Н.Я. Виленкин, В.И. Жохов, А.С.Чесноков, С.И. Шварцбурд. / М.: Мнемозина, 2011, мультимедиа проектор, компьютеры, документ – камера, презентация в PowerPoint, электронные тренажёры, рабочие тетради, жетоны – снежинки, таблицы № 1 и № 2, карточки (см Приложения № 1, 2, 3).
Содержание учебного материала
I. Мотивация к учебной деятельности ( 2 мин )
— актуализировать требования к ученику со стороны учебной деятельности;
— создание условий для возникновения у учеников внутренней потребности включения в учебную деятельность.
-Здравствуйте ребята. Сегодня у нас на уроке много гостей. Давайте поприветствуем их своими светлыми, добрыми улыбками и порадуем их своими знаниями. Я желаю вам хорошего и бодрого настроения, как этот прекрасный зимний день. (играет музыка) Слайд № 1 .
— Ребята, теперь вы можете сесть поудобнее. Проверим, все ли у нас готово к уроку: учебник, тетрадь, опросные листы, дневник.
— Что еще нам пригодится на уроке? ( аккуратность, внимание, знания, сообразительность, ум…. .).
Организует актуализацию требований к ученику со стороны учебной деятельности.
Создаёт условия для возникновения у учеников внутренней потребности включения в учебную деятельность.
Устанавливает тематические рамки.
Внимательно слушают учителя и отвечают на его вопросы.
организовывать своё рабочее место под руководством учителя.
Умение слушать и понимать речь других.
II. Построение проекта выхода из затруднения (цель, тема). ( 4 мин )
— организовать постановку цели урока;
На экране слайд № 2 :
│2х — 8│= 0; │3х — 6│= 0;
│2х — 5│= — 7; │х — 0,56│= -15.
1. Ребята, как вы думаете, чем сегодня мы будем заниматься на уроке?
( Решать уравнения с модулем ).
Вывод темы урока (проблемы урока). « Решение уравнений с модулем»
Повторить!! На экране выводится слайд № 3 с темой урока .
2. Ребята, скажите, пожалуйста, где находится неизвестная величина во всех уравнениях? ( под знаком модуля ).
3. Чем отличаются эти уравнения?
( тем, что в правой части уравнения стоят положительные числа, 0 и отрицательные числа )
4.Кто разделит их по группам?
5.Ребята, сделайте вывод о том, по какому принципу вы их разделили.
( В первой группе в правой части стоит положительное число (а > 0), во второй – нуль (а = 0), в третьей – отрицательное число
Организует проблемную ситуацию для выявления проблемы урока .
Организует актуализацию умений делить на группы по заданному признаку
Организует обобщение актуализированных знаний.
Под руководством учителя выявляют и проговаривают проблему урока.
4. С помощью учителя дают характеристику уравнениям и делят их по группам.
5. Ученики высказывают свои предположения.
определение последовательности промежуточных целей с учётом конечного результата; составление плана и последовательности действий
постановка и формулирование проблемы
анализ объектов с целью выделения признаков
III. Актуализация знаний и фиксация затруднений в деятельности. ( 1 мин )
— организовать повторение и закрепление полученных ранее знаний.
6.Что нужно уметь и знать, чтобы решить эти уравнения?
( 1)Знать, что значит решить уравнение.
3)Уметь решать уравнения.
Учитель выводит на экране эти предположения ( слайд № 5 ).
Отвечают на вопросы.
Регулятивные УУД: составление плана и последовательности действий
IV. Реализация построенного проекта.
— реализовать построенный проект в соответствии с планом;
— организовать устранение и фиксирование преодоления затруднения;
Самостоятельная работа с самопроверкой по эталону.
— зафиксировать новое содержание урока.
7. Итак, мы составили план урока.
— Сегодня мы будем работать в группах. Чтобы группа могла получить хорошую оценку за урок, каждый ученик должен хотя бы раз ответить и заработать жетон для своей группы и для себя.
Для повторения теоретического материала к доске выходят три ученика, получившие в начале урока треугольные фигурки, и отвечают по листу опроса. Если ученик неверно ответил на вопрос или нечетко сформулировал правило, то на этот же вопрос отвечает следующий ученик. Если первый ученик справился с ответом, то на второй вопрос отвечает другой ученик и т.д. За каждый верный ответ учитель выдаёт жетон ученику (см. приложение № 2).
Параллельно с учащимися, получившими треугольники, работают остальные ученики в группах: решают уравнения, которые были представлены на втором этапе урока. Теперь эти уравнения предложены в качестве раздаточного материала для каждой группы. После выполнения задания на экране появляются ответы, а учащиеся внутри группы способом взаимопроверки оценивают друг друга.
После окончания работы всеми учащимися, ученики, решавшие уравнения в группах, озвучивают поставленную оценку, аргументируя её.
Организует коррекционную работу
Проводится работа со слабыми (треугольники).
Видео:6 класс. Решение уравнений с модулями.Скачать

Решение уравнений с модулем. 6-й класс
Разделы: Математика
Класс: 6
Тип урока: урок постановки учебной задачи.
Цели урока:
- обучение решению уравнений со знаком модуля на основе применения свойств уравнений;
- развитие навыков теоретического мышления с применением навыков элементарных операций с модулем и определения модуля;
- воспитание внимания и умения анализировать полученное решение, участвовать в диалоге с товарищами, учителем.
I. Повторение пройденного
Внимательно рассмотрите предложенные уравнения:
1) | х | = х + 5;
2) | х | = – 3х + 5;
3) | х – 3 | = 2;
4) | 2х – 5 | = х – 1;
5)= х – 1;
6) | 2х – 5 | = 2 – х;
7) | х + 2 | = 2(3 – х);
8) | 3х – 5 | = | 5 – 2х | ;
9) | х – 2 | = 3 | 3 – х | ;
10) | | х – 1 | – 1 | = 2.
Задание 1. Распределите данные уравнения по группам.
Учащиеся сначала выделили две группы. В первую группу вошли уравнения 1) –3), 5) –7). Ко второй группе были отнесены уравнения 8) и 9). Затем учащиеся заметили уравнение 10), содержащее знак модуля два раза. Окончательно было выделено три группы: 1-я группа – модуль содержится в левой части уравнения; 2-я группа – модуль содержится в обеих частях уравнения; 3-я группа – в уравнении содержится двойной модуль.
Учитель. Какую главную задачу мы должны будем решить сегодня на уроке?
Учащиеся. Мы должны научиться решать уравнения.
Учитель. Да. Но посмотрите еще раз на все эти уравнения и выделите их общую особенность.
Учащиеся. Все они содержат модуль.
Учитель. Как точнее сформулировать задачу нашего урока?
Учащиеся. Применять определение модуля при решении данных уравнений.
Учитель. Действительно, эту задачу мы и должны решить на уроке. По-другому ее можно сформулировать так: “Как решать уравнения с модулем?” Какие понятия, определения могут быть полезны при решении этой задачи?
1. Что такое модуль?
2. Определение модуля.
Учитель. Вспомним, что такое модуль.
Учащиеся. По определению:
| а | =  | если а > 0 если а 0 (число положительное).
а) Если х – 3 Видео:Как решать уравнения с модулем ( Математика 6 класс )Скачать  Уравнения с модулем в 6 классеУравнения с модулем в 6 классе сводятся к простейшим уравнениям, решение которых опирается на определение модуля. Рассмотрим некоторые из таких уравнений. Начнем с такого вида: Решаем это уравнение как линейное: неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки: Теперь обе части уравнения делим на число, стоящее перед модулем икса: Данное уравнение не имеет решений, так как модуль не может быть отрицательным числом. Ответ: нет решений. Также в 6 классе встречаются уравнения с модулем вида Это уравнение — почти простейшее уравнение с модулем, соответственно, решаем его аналогично: Каждое из полученных уравнений — линейное. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки: Более сложные уравнения с модулем в 6 классе представляют собой сочетание обоих видов. Сначала рассмотрим это уравнение как линейное (все выражение, стоящее под знаком модуля, считаем одним неизвестным): Данное уравнение решим как простейшее уравнение с модулем: Видео:Модуль числа. Практическая часть. 6 класс.Скачать  141 Commentsя ещё не разу не пользовалась этим сайтом Очень хороший сайт… реально помог Помогите решить,пожалуйста, -|х|=3 -|х|=3 Помогите решить, пожалуйста: |х|-2= -3 |х|= -3 + 2; |х|= -1. Нет решений, так как модуль не может быть равным отрицательному числу. Будьте добры, объясните решение примера с модулем в модуле: PS. х в квадрате. |-|3-х²||=6; |3-х²|=6; 3-х²=±6; 3-х²=6 или 3-х²=-6; х²=-3 или х²=9. Первое из уравнений не имеет корней, корни второго — x=3 и x=-3. Помогите решить уравнение пожалуйста 3|x+4|-7=18 3|x+4|=18+7; 3|x+4|=25; |x+4|=25/3; x+4=±8 1/3 помогите решить задачи модуль х=1 модуль выражения х-3=1 модуль х=х Если |х|=1, то х=1 или х=-1. Спасибо вам очень сильно помогло.Вседа были проблемы, а сейчас нету Бексултан, если все новые темы разбирать по мере изучения, проблем не будет. Учитесь, и всё у Вас получится! Помогите, пожалуйста, (3+|x|)(4-2|x|)=0 Это уравнение типа произведение равно нулю. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый их множителей:3+|x|=0 или 4-2|x|=0. Отсюда |x|=-3 или 2|x|=4, |x|=2. Уравнение |x|=-3 не имеет корней, уравнение |x|=2 имеет два корня: х=2 и х=-2. Помогите пожалуйста решить: 0,63:|x|=0,91; |x|=0,63:0,91; |x|=9/13: х=9/13 или х= -9/13. Помогите ещё, пожалуйста,вот это |5х+2|-11=21 |5х+2|=21+11; |5х+2|=32; 5х+2=32 или 5х+2=-32; 5х=30, х=6 или 5х=-34, х=-6,8. Помогите пожалуйста решить x=9 или x=-9. Помогите решить пожалуйста: А что, собственно, требуется найти? Найти чему равно А , а то есть решить уравнение Получается, что у Вас в одном уравнении две переменные ещё и х. Нужно либо еще одно уравнение, либо Вы что-то в условии напутали. Это пример, который дан в тесте Что-то не то с условием. Может, пришлёте фото задания? 1)Если х≥0, то |х|=х и уравнение принимает вид х²=-4х, корни которого равны 0 и -4. Условию х≥0 удовлетворяет только х=0. -|x|=10-7 Помогите пожалуйста-x=9 и второе -x=-3 Если -x=a, то x=-a. Помогите, пожалуйста, решить Модуль (х+Y)=0 Лилия, решить это уравнение не получится. Можно сказать только, что если модуль x+y равен нулю, то и x+y=0, а значит, x=-y, то есть x и y — противоположные числа. Помогите решить |||2х+7|-3|+6=6 Одна скобка лишняя. ||2х+7|-3|=6-6; ||2х+7|-3|=0;|2х+7|-3=0; |2х+7|=3. Далее — 2 варианта: Помогите пожалуйста решить 7,4-3,6|x|=18-4|x| Помогите решить 0x=8 помогите решить |x|-6=-9 |x|=-9+6 Помогите решить пожалуйста 2|x|+|1-3x| при x=1,2 Это же не уравнение. Просто подставляем вместо x 1,2 и вычисляем: Помогите решить 3|х-6|+4у,если х= две целых 5/7,у=-3/7 Олеся, Вы вполне можете найти значение этого выражения самостоятельно. Нужно просто подставить вместо x и y их значения: помогите решить |5x+1|=3 Антон, ведь сверху есть аналогичные примеры. Один раз разберитесь, и проблем с такими заданиями больше не будет. Помогите решить 3х-2|у-1| при х=-1, у=-4 и объясните как вы решили Вместо x и y подставляем их значения х=-1, у=-4: Помогите решить Здесь можно только упростить.Так как |-x|=|x|, то x-4=2 или x-4= -2. Решаем оба уравнения по отдельности. Получаем два корня: Помогите решить |3x + 2 | = | x — 1 | Самый простой способ решения уравнений такого вида — возвести обе части уравнения в квадрат (если Вы уже знаете, как решаются квадратные уравнения). Помогите решить Умножим обе части уравнения на -1: Помогите решить Так как |-4|=4, то уравнение сводится к уравнению |x|=4, откуда x=4, x=-4. Помогите пожалуйста! |x|= -x.Это равенство верно для любого неположительного числа (то есть x≤0). Памагите решить. /2х/-y=0 y=4 Подставив вместо y 4, получаем уравнение |2х|-4=0. Отсюда |2х|=4; 2х=4 или 2х=-4. //а+5/-а/ при том что а=-6. помогите пожалуйста помогите пожалуйста 5|x|=4,2 |x|= 4,2:5 Здравствуйте, помогите решить пожалуйста уравнение: Можно рассмотреть 2 варианта раскрытия модулей. Помогите пожалуйста решить (a-3)(a+2)x=a+2 Это — линейное уравнение. Уравнение вида ax=b при a≠0 имеет единственный корень x=b/a. Помогите придумать уровнение с модулем из 6 класса Помогите пожалуйста решить Если x Олег 15.02.2019 17:31 Ответить Помогите решить уравнение ||x|-9|=3. ||x|-9|=3 помогите пожалуйста 7х+4|x|=-3 1) если x>0, |x|=x Помогите пожалуйста решить:||x|-5|||=6 Артём, у Вас знаков модуля больше, чем нужно:||x|-5|=6 Можно пожалуйста обьеснить чему равно N если N Светлана Михайловна 27.05.2019 20:06 Ответить Условие N Захар 27.05.2019 20:37 Ответить помогите пожалуйста решить −21:|x|=0,04−7,04. Антон, а давайте Вы попробуете решить этот пример самостоятельно, а я его проверю. Если будут ошибки, помогу. Идёт? ответ будет x1=-3 x2=3 ? Антон, обе части линейного уравнения делим на число, стоящее ПЕРЕД иксом. Огромное спасибо я понял что я сделал не так Антон, успехов Вам в изучении математики! Не бойтесь решать самостоятельно и делать ошибки. Это же учёба. А вот если ничего не делать, то не получится научиться. помогите пожалуйста решить 3|x-2|-|2-x|/-3=-5,2 Татьяна, |2-x|/(-3)? Для начала Вам подсказка: |a-b|=|b-a| спасибо я уже решила Можно еще вопрос-нужно найти значение выражения х*|у| если х=-2, у=-3/4 Модуль отрицательного числа равен противоположному числу. Например, |-9|=9. Дальше — дело техники. Успехов Вам в учёбе, Татьяна! Используйте время карантина наилучшим образом. Помогите пожалуйста решить уравнение -|0.7|•у=|0.42| Помогите решить (|7,6|-|-8,1|):|-5| Добрый вечер, помогите решить ||x|-5|=6 ||x|-5|=6 Здравствуйте, уважаемая Светлана Михайловна! Помогите, пожалуйста разобраться. Ребенок на вступительном тестировании в лицей решал пример: 3-|4|x|-7|=-4^2 (четыре в квадрате, но с минусом большой вопрос: что тут имелось в виду — квадрат числа с минусом? Тогда, может, скобки должны были быть? Или просто ребенок неправильно переписал пример). Что Вы скажете по поводу решения данного примера? Во-первых, если бы в квадрат возводили -4, то обязательно должны быть скобки. Спасибо огромное за разъяснение и за этот сайт! Очень помогает вспомнить свою школьную программу и прояснить все узкие места для современных школьников :)). СПАСИБО! Ольга, Вам спасибо за теплые слова! Здравствуйте, помогите пожалуйста решить уравнение с модулями /5-/4x-7//*(2x+19)=0 Светлана Михайловна, помогите решить уравнение. |7x-57,1|-|-14/3|=|31/3| Помогите, пожалуйста: Найдите значение выражения: | — 4 | + |1 – 3х| , при х = 2,4. Здравствуйте, помогите пожалуйста решить уравнение с модулем |4-|1-2x||=22 4-|1-2x|=22 или 4-|1-2x|=-22 Здравствуйте Помогите решить пример Объясните пожалуйста как решать: 4(y+1)-3|x+5| при x: 7, y: -2 Подставляем x=7 и y=-2 в данное выражение: Помогите пожалуйста с уравнение |3х+2|=|х-1| заранее спасибо! Самый простой способ — возвести в квадрат обе части и решить полученное квадратное уравнение. В 6 классе квадратных уравнений решать ещё не умеем, действуем иначе. Каждый модуль можно раскрыть с знаками плюс и минус. Таким образом, получаем 2 случая: если знаки модулей одинаковы и если они разные. помогите решить |6+5x|=2 и еще один |8-|x+2||=7 1)|6+5x|=2 Почему |x|=10, то x=-10;x=10 Богдан, потому что модуль числа a — это расстояние от начала отсчёта (точки О с координатой 0) до точки с координатой а. На координатной прямой на расстоянии 10 от нуля находятся две точки — точка с координатой 10 и точка с координатой -10. Помогите пожалуйста решить 3•|0,2х+4|-3=-5,4 3∙|0,2х+4|=-5,4+3; 3∙|0,2х+4|=-2,4; |0,2х+4|=-2,4:3; |0,2х+4|=-0,8. Нет решений, так как модуль не может быть отрицательным. 🔍 ВидеоКак решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать  Уравнение с модулемСкачать  Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать  Контрольная работа. Уравнения с МОДУЛЕМСкачать  Уравнения с модулем 🫢Скачать  Математика. 6 класс. Линейное уравнение, содержащее переменную под знаком модуля /20.01.2021/Скачать  Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать  Уравнения с модулемСкачать  Решение уравнений с модулем в 6 классеСкачать  ВПР 6 КЛАСС. Задание с модулем.Скачать  Модуль числа. 6 класс.Скачать  Модуль числа, 6 классСкачать  Уравнение с МОДУЛЕМСкачать  Уравнения с модулем. Часть 2 | Математика | TutorOnlineСкачать  Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать  |
 = х – 1;
= х – 1; 
 0, то есть х
0, то есть х  3, то | х – 3 | = х – 3;
3, то | х – 3 | = х – 3;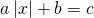
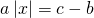
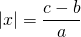
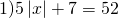
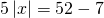
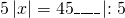
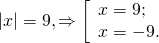

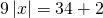
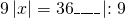
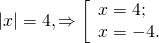
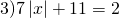
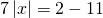
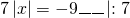
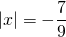
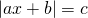
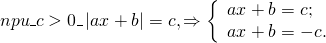 0_left| right| = c, Rightarrow left< begin ax + b = c;\ ax + b = — c. end right.]» title=»Rendered by QuickLaTeX.com»/>
0_left| right| = c, Rightarrow left< begin ax + b = c;\ ax + b = — c. end right.]» title=»Rendered by QuickLaTeX.com»/>