Математика 6 класс отношения и пропорции уравнения (3 видео)

Содержание

Составление и решение пропорций в математике
Пропорции — что это в математике
Основное свойство пропорции, правило
Составление и решение пропорций
Примеры уравнений с решением для 6 класса
Отношения и пропорции 6 класс презентация к уроку по математике (6 класс)
Скачать:
Предварительный просмотр:
Подписи к слайдам:
По теме: методические разработки, презентации и конспекты
Математика. 6 класс
📺 Видео

Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Составление и решение пропорций в математике

Видео:Пропорция. Основное свойство пропорции. 6 класс.Скачать

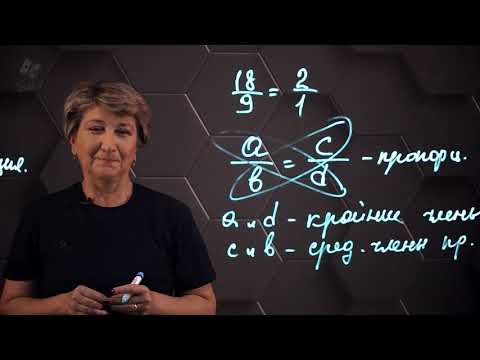
Пропорции — что это в математике

Валя съела 3 яблока из пяти. Какую часть яблок съела Валя?

Вначале узнаем, какую часть яблок составляет 1 яблоко. Всего у Вали было 5 яблок, значит, одно из них — это 1 5 часть всех яблок. Тогда 3 съеденных яблока составляют 3 5 всех яблок.

Тот же ответ получим, если 3 разделим на пять.

Получается, что 3 яблока соотносятся с пятью яблоками как 3 к 5.

Другой вариант записи ответа отмечают в виде десятичной дроби и процентов: 3 5 = 0 , 6 или 60%.

Отношением двух чисел называют частное этих чисел.

Отношение показывает, во сколько раз одно число больше другого. Или какую часть первое число составляет от второго.

Термин «отношение» применяют в случаях, когда нужно выразить одну величину в долях другой. Например, одну площадь в долях другой площади. Это операцию выполняют с помощью деления.

Делимое в выражении отношения называют предыдущим членом. Делитель называют последующим членом.

В задаче 1 предыдущий член — это 3, последующий — 5.

Если есть два равных отношения, то они образуют пропорцию.

Пропорцией называют равенство двух отношений.

Даны два отношения: 3,8:2 и 5,7:3.

Можно ли составить из этих выражений пропорцию?

Найдем значения каждого из отношений:

3 , 8 : 2 = 1 , 9 ; 5 , 7 : 3 = 1 , 9 .

Значения выражений оказались равными, значит, эти отношения равны.

Тогда можно записать равенство: 3,8:2=5,7:3.

Такое равенство называется пропорцией.

Ответ: да, можно составить из этих отношений чисел пропорцию.

С помощью буквенных символов пропорцию можно записать так: a : b = c : d или a b = c d .

Полученное равенство читают: «Отношение a к b равно отношению c к d» или «a относится к b, как c относится к d».

Числа a и d в пропорции называют крайними членами пропорции.

Числа b и c — средними членами пропорции.

Назовите крайние и средние члены пропорции 42:6=49:7.

Крайние члены пропорции — 42 и 7.

Средние члены пропорции — 6 и 49.

Определите средние члены пропорции 25 5 = 35 7 .

Средние члены пропорции — 5 и 35.

Понятие «пропорция» пришло из латинского языка. Слово в переводе означает соразмерность, определенное соотношение частей между собой.

Видео:ПРОПОРЦИЯ 6 класс математика отношения и пропорцииСкачать

Основное свойство пропорции, правило

Основное свойство пропорции

В верной пропорции произведение крайних членов равно произведению средних членов:

Определите, верна ли пропорция 6:2=9:3.

В верной пропорции произведение крайних членов равно произведению средних членов.

Произведение крайних членов равно произведению 6 и 3. Получим 6 * 3 = 18 .

Произведение средних членов равно произведению 2 и 9. Получим 2 * 9 = 18 .

Значит, 6:2=9:3. Пропорция верна.

Обратное утверждение тоже верно:

Если произведение средних членов равно произведению крайних членов, то пропорция верна.

Пропорция 60:12=10:2 верна, потому что 60 * 2 = 12 * 10 = 120 .

Если поменять в это пропорции местами средние члены, получим 60:10=12:2. Эта пропорция тоже верна. При перестановке произведение крайних и средних членов не изменилось.

Если в пропорции поменять крайние члены — 2:10=12:60, то произведение тоже не изменится.

Пропорция будет верной, если поменять местами средние члены или крайние члены.

Если какой-то из членов пропорции неизвестен, то его можно найти.

По основному свойству пропорции можно найти ее неизвестный член, если все остальные компоненты известны.

Найдите неизвестный член пропорции: 4,8:b=8:2,5.

Используем основное свойство пропорции: произведение крайних членов = произведению средних членов.

Получим 4 , 8 * 2 , 5 = b * 8 .

b = 4 , 8 * 2 , 5 : 8 ;

Видео:КАК РЕШАТЬ ПРОПОРЦИИ?Скачать

Составление и решение пропорций

Запишите пропорцию: 6 так относится к 18, как 9 относится к 27.

Слово «относится» заменяем на знак деления.

Получаем два отношения: 6:18 и 9:27.

Если эти два отношения равны, то получаем верную пропорцию.

6 : 18 = 9 : 27 ; 1 3 = 1 3 , получили верную пропорцию.

Запишите пропорцию и проверьте ее: отношение 2 к 1 4 равно отношению 3 к 1 15 .

Записываем отношения: 2 1 4 и 3 1 15 .

Составляем пропорцию: 2 1 4 = 3 1 15 .

Проверяем, верна ли пропорция.

Для этого воспользуемся основным свойством пропорции: произведение крайних членов = произведению средних членов.

2 * 1 15 ≠ 1 4 * 3 ; 2 15 ≠ 3 4 . Условие равенства произведений не выполнилось, значит, пропорция не верна.

Определите, верна ли пропорция: 1 , 4 0 , 7 = 3 , 4 1 , 7 .

Чтобы проверить, верна ли пропорция, воспользуемся основным свойством пропорции.

Запишем произведения крайних и средних членов пропорции:

1 , 4 * 1 , 7 = 2 , 38 ; 0 , 7 * 3 , 4 = 2 , 38 .

Значит, произведение крайних членов равно произведению средних членов.

1 , 4 * 1 , 7 = 0 , 7 * 3 , 4 ; 2 , 38 = 2 , 38 .

Вывод: пропорция верна.

Видео:Отношение двух чисел. 6 класс.Скачать

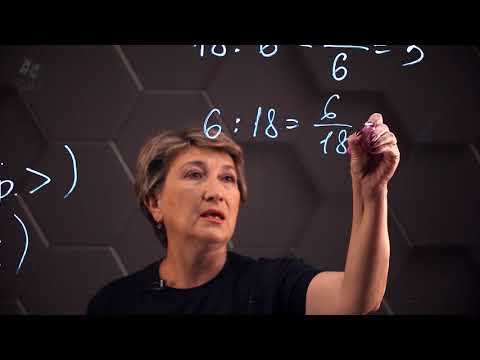
Примеры уравнений с решением для 6 класса

Решите уравнение: 8 , 8 4 2 5 = n 0 , 12 .

Чтобы найти неизвестный член пропорции, используем основное свойство пропорции. Находим произведение крайних и средних членов. Выражаем неизвестный компонент.

8 , 8 4 2 5 = n 0 , 12 ; 8 , 8 * 0 , 12 = 4 2 5 * n . Из равенства выражаем n : n = 8 , 8 * 0 , 12 4 2 5 Представим смешанное число 4 2 5 в виде десятичной дроби. Для этого приведем дробную часть смешанного числа к дроби со знаменателем 10 : домножим числитель и знаменатель 2 . 4 2 5 = 4 2 * 2 н а 5 * 2 = 4 4 10 . Такое смешанное число записываем в виде десятичной дроби, отделяя целую часть запятой: 4 4 10 = 4 , 4 . Тогда n = 8 , 8 * 0 , 12 4 , 4 . Сокращаем получившуюся дробь: 0 , 12 и 4 , 4 делятся на 4 . n = 8 , 8 * 0 , 03 1 , 1 ; 8 , 8 и 1 , 1 делятся на 1 , 1 . n = 8 * 0 , 03 1 ; n = 0 , 24 .

Найдите неизвестный член пропорции: 1 1 2 : 2 1 4 = 6 : m .

Используем основное свойство пропорций. Записываем равенства произведений крайних и средних членов.

1 1 2 * m = 2 1 4 * 6 . И выражаем m : m = 2 1 4 * 6 : 1 1 2 . Переводим смешанные числа в неправильные дроби: m = 2 * 4 + 1 4 * 6 : 1 * 2 + 1 2 ; m = 9 4 * 6 : 3 2 . Натуральное число переводим в обыкновенную дробь со знаменателем 1 и умножаем на первую дробь: m = 9 4 * 6 1 : 3 2 ; m = 9 * 6 4 * 1 : 3 2 . Чтобы разделить обыкновенные дроби, нужно домножить дробь на взаимно обратную данной: m = 9 * 6 4 * 1 * 2 3 ; m = 9 * 6 * 2 4 * 1 * 3 . Сокращаем получившееся выражение. 4 и 2 делятся нацело на 2 . 9 и 3 делятся нацело на 3 . m = 3 * 6 * 1 2 * 1 * 1 . Для чисел 6 и 2 общий делитель 2 : m = 3 * 3 * 1 1 * 1 * 1 ; m = 9 .

Решите уравнение: 0,25:x=3,75:3.

По основному свойству пропорции получим: 0 , 25 * 3 = x * 3 , 75 .

x = 0 , 25 * 3 : 3 , 75 ; x = 0 , 75 : 3 , 75 . Делить на десятичную дробь нельзя. Преобразуем ее в натуральное число.

После запятой в дроби 3 , 75 два знака, значит, нужно домножить ее на единицу с таким оличеством нулей. Это сто.

Но чтобы выражение осталось неизменным, нужно домножить на сто и делимое.

x = 0 , 75 * 100 : 3 , 75 * 100 ; x = 75 : 375 ; x = 0 , 2 .

Найдите неизвестное: k : 3 1 2 = 0 , 4 : 2 4 5

Чтобы найти неизвестный компонент пропорции, нужно воспользоваться основным свойством дроби.

По основному свойству дроби произведение крайних членов равно произведению средних членов.

Получим: k * 2 4 5 = 3 1 2 * 0 , 4 .

Выразим k : k = 3 1 2 * 0 , 4 : 2 4 5 .

Переведем 0,4 в обыкновенную дробь: 0 , 4 = 4 10 . Эта дробь сократима: числитель и знаменатель делятся на 2 нацело: 4 10 = 4 : 2 10 : 2 = 2 5 .

Записываем полученное выражение:

k = 3 1 2 * 2 5 : 2 4 5 .

1 действие — умножение.

Переводим смешанное число в неправильную дробь и умножаем на вторую: числитель на числитель, знаменатель на знаменатель.

3 1 2 * 2 5 = 3 * 2 + 1 2 * 2 5 = 7 2 * 2 5 = 7 * 2 2 * 5 .

Сокращаем дробь: есть одинаковые числа в числителе и знаменателе.

2 действие — деление.

Теперь делим полученное число на 2 4 5 .

Смешанное число переводим в неправильную дробь.

Умножаем 7 5 на взаимно обратную дробь.

7 5 : 2 4 5 = 7 5 : 2 * 5 + 4 5 = 7 5 : 14 5 = 7 5 * 5 14 = 7 * 5 5 * 14 = 7 * 5 5 * 14 = 7 14 = 1 2 = 0 , 5 .

Видео:6 класс, 20 урок, ОтношенияСкачать

Отношения и пропорции 6 класс
презентация к уроку по математике (6 класс)

Нашла эту презентацию на просторах интернета.Очень понравилась. Буду признательна, если кто-то подскажет автора

Видео:ОТНОШЕНИЯ И ПРОПОРЦИИ 6 класс математикаСкачать

Скачать:

Вложение	Размер
proportsii.ppt	1.95 МБ

Предварительный просмотр:

Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 1 часть. 6 класс.Скачать

Подписи к слайдам:

Математика 6 класс Пропорции и отношения

Отношения. Основное свойство отношений. Пропорция. Основное свойство пропорций. Решение уравнений на основе свойств пропорции. Случайные события. Вероятность случайного события. Процентное отношение двух чисел. Процентные расчеты. Задачи экономического содержания. Прямая пропорциональная зависимость. Задачи на пропорциональное деление . Окружность. Длина окружности. Круг. Площадь круга. Круговой сектор. Столбчатые и круговые диаграммы. План учебного материала

Отношения. Основное свойство отношений.

Частное двух чисел называют отношением этих чисел. Отношение показывает, во сколько раз одно число больше другого или какую часть составляет одно число от другого . Отношения 3:5 2,7:0,4

Отношения 3:5 частное дробь отношения

Отношение двух чисел не изменится, если каждое из них умножить или разделить на одно и то же число, отличное от нуля. Основное свойство отношения Оба члена пропорции можно поделить на их общий делитель. Отношение дробных чисел можно заменить отношением натуральных чисел.

Пропорция. Основное свойство пропорции.

Пропорция Равенство двух отношений называют пропорцией . a, d – крайние члены пропорции c, b – средние члены пропорции a : b = c : d , или при b ≠ 0 і d ≠ 0

Произведение крайних членов каждой пропорции равно произведению ёё средних членов. Если a : b = c : d то a · d = c · b Основное свойство пропорции 4 : 2 = 8 : 4 то 4 · 4 = 8 · 2

Чтобы найти неизвестный крайний член пропорции, достаточно произведение ёё средних членов поделить на известный крайний. Чтобы найти неизвестный средний член пропорции, достаточно произведение ёё крайних членов поделить на известный средний. Неизвестный член пропорции

Решение уравнений на основе свойств пропорции.

Решите уравнение x : 2 = 3 : 11

Случайное событие. Вероятность случайного события.

Событие Событие – то, что происходит, случается. Событие – это явление, которое обязательно наблюдалось большее или меньшее количество раз при многоразовом повторении испытания. Подкидываем монету – испытание, появление орла – событие. Достаём лампу из коробки – испытание, лампа с браком – событие.

Событие СОБЫТИЕ СЛУЧАЙНОЕ РАВНОВОЗМОЖНОЕ НЕВОЗМОЖНОЕ ДОСТОВЕРНОЕ

Вероятность случайного события Вероятностью события — называют отношение числа благоприятных для этого события результатов к числу всех возможных результатов. где А – событие ; Р(А) – вероятность события N – общее количество равновозможных и несовместных событий N (А) – количество событий, которые благоприятствуют событию

Процентное отношение двух чисел. Процентные расчёты. Задачи экономического содержания.

Процентное отношение Если отношение двух чисел выражают в процентах, то его называют процентным отношением . Один процент – это одна сотая часть 1% = 0,01 50% = 0,5 100% = 1 200% = 2

Процентное отношение Существует три основных вида задач на проценты нахождение процентов от числа нахождение числа по значению его процента нахождение процентного отношения двух чисел

Процентное отношение Необходимо впахать поле, площадь которого равна 300 га. В первый день трактористы выполнили 40% задания. Сколько гектаров они вспахали за первый день? S = 300 га 40 % за І день ? га 300 га – 100 % х га – 40 % складываем пропорцию находим неизвестный член пропорции

Процентное отношение В первый день трактористы вспахали 120га , что составляет 40% поля. Найдите площадь всего поля. S = ? га 40 % за І день 120 га 120 га – 40 % х га – 100 % складываем пропорцию Находим неизвестный член пропорции

Процентное отношение Необходимо вспахать поле, площадь которого 300га. В первый день трактористы вспахали 120 га. Сколько процентов всего поля они вспахали в первый день? S = 300 га ? % за І день 120 га 300 га – 100 % 120 га – х % складываем пропорцию Находим неизвестный член пропорции

Прямая пропорциональная зависимость.

Прямая пропорциональная зависимость Две величины называют прямо пропорциональными , если с увеличением (уменьшением) значений одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз. Скорость, км/ч 60 60 60 60 Время, ч 1 2 3 4 Путь, км 60 120 180 240

Обратно пропорциональная зависимость Две величины называют обратно пропорциональными , если с увеличением (уменьшением) значений одной из них в несколько раз значения другой уменьшаются (увеличиваются) во столько же раз. Скорость, км/ч 50 60 100 150 Время, ч 6 5 4 3 Путь, км 300 300 300 300

Задачи на пропорциональное деление.

Задачи на пропорциональное деление Чтобы поделить число на части, пропорциональные данным числам, нужно поделить его на сумму данных чисел и найденное частное умножить на каждое из них. Проволоку длиной 60 м разрезали на 3 части, длины которых пропорциональны числам 2, 3 і 5. Найдите длины этих частей проволоки.

Задачи на пропорциональное деление Отдельным видом задач на пропорциональное деление являются задачи на нахождение двух чисел по их сумме и отношению. Задача 1. Поле площадью 100 га поделили на две части, площади которых пропорциональны числам 2 и 3. Найдите площади этих частей. Задача 1. Поле площадью 100 га поделили на две части, площади которых относятся как 2 : 3. Найдите площади этих частей.

Окружность. Длина окружности. Круг. Площадь круга. Круговой сектор.

Окружность О – центр окружности; ОА = r – радиус окружности (отрезок, который соединяет любую точку окружности с его центром); MN = d – диаметр (отрезок, который соединяет две точки окружности и проходит через его центр) Любой диаметр окружности в 2 раза длиннее чем радиус, то есть d = 2 r . A O M N

Длина окружности  ≈ 3,14 это отношение длины окружности к диаметру O r

Круг Объединение окружности и его внутренней области называют кругом . Окруж ность круг внутренняя область

Площадь круга O r

Круговой сектор Часть круга, ограниченная двумя его радиусами, называется круговым сектором . O r r

Столбчатые и круговые диаграммы.

Диаграммы Для наочного изображения числовых значений различных величин используют диаграммы . Слово “ диаграмма ” греческого происхождения, что означает “ рисунок ”. Диаграмма – это символический рисунок, который наочно иллюстрирует соотношения между значениями величин. Чаще всего используют диаграммы линейные круговые столбчатые

Линейная диаграмма Линейная диаграмма состоит из нескольких отрезков. 175 180 185 190 195 200 73 95 80 120 85 150 Волга Дунай Урал Дн е пр Дон Днестр 3530 3645 3542 3750 3560 3900

Столбчатая диаграмма Столбчатая диаграмма это та же линейная диаграмма, но в ней отрезки заменены на прямоугольники.

Круговая диаграмма Круговая диаграмма имеет вид круга, разделенного радиусами на части (секторы). Поэтому такие диаграммы называют так же секторными.

Видео:Решение уравнений, имеющих вид пропорции, с использованием основного свойства пропорции Математика 6Скачать

По теме: методические разработки, презентации и конспекты

Урок обобщения и систематизации знаний в 6 классе «Отношения и пропорции»

Этот урок можно провести в конце изучения темы «Отношения и пропорции», перед проведением контрольной работы, с целью отработать навыки учащихся в решении задач на прямую и обратную пропорциональность.

Самостоятельная работа по теме «Отношения и пропорции» 6 класс

Самостоятельная работа по теме «Отношения и пропорции» 6 класс.

Реализация требований ФГОС ООО при обучении учащихся 6 класса теме: «Отношения и пропорции»

Конспект урока математики в 6 классе по теме: «Отношения и пропорции».

Данный материал может быть применён в сочетании с любым УМК.

Методическая разработка урока математики в 6 классе по теме «Отношения и пропорции» с акцентом на здоровьесберегающую тему.

Предлагаемый материал был представлен на семинаре по здоровьесберегающим технологиям. Это план урока математики в 6 классе по теме «Отношения и пропорции» с авторкой презентацией.

Зачетная работа для учащихся 6 класса по теме «Отношения и пропорции»

Зачетная работа для учащихся 6 класса по теме «Отношения и пропорции».

Разработка урока математики с использованием тестовых образовательных технологий в 6 классе. Тема: «Отношения. Масштаб. Пропорции».

Разработка урока математикис использованием тестовых образовательных технологийТестирование ( с использованием тестовой образовательной технологии ) в 6 классе( тестовые задания открытого типа с кратк.

Видео:Отношения - примеры и задачи. Математика 6 классСкачать

Математика. 6 класс

Конспект урока

Перечень рассматриваемых вопросов:

Понятие пропорции.
Основное свойство пропорции.
Как правильно составить пропорцию.
Как найти неизвестный член пропорции.

Равенство двух отношений называют пропорцией.

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.

Рассмотрим 3 способа нахождения неизвестного члена пропорции.

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

№2. Тип задания: Подстановка элементов в пропуски в тексте.

Найдите неизвестный член пропорции.

Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.