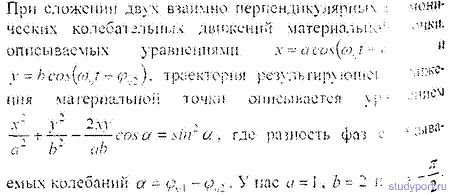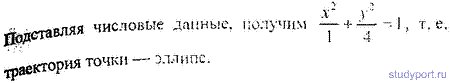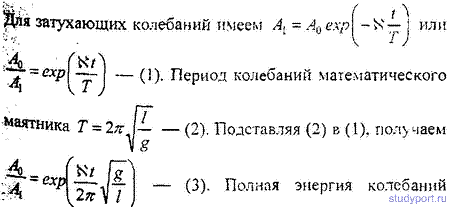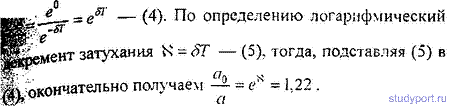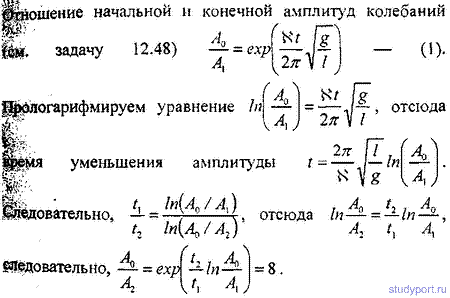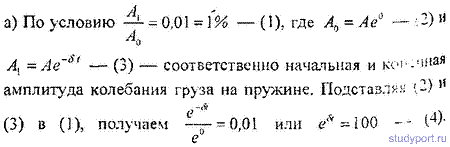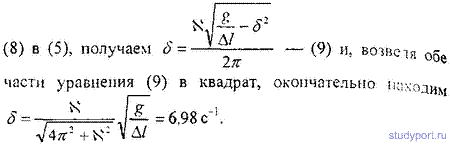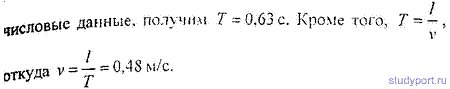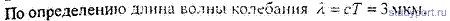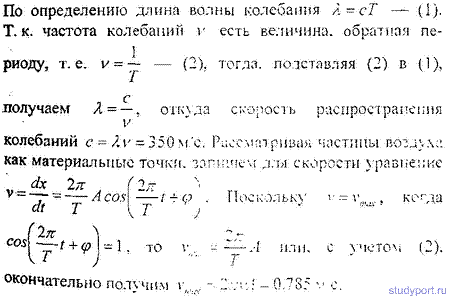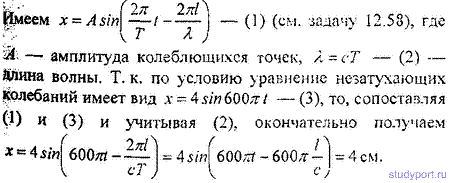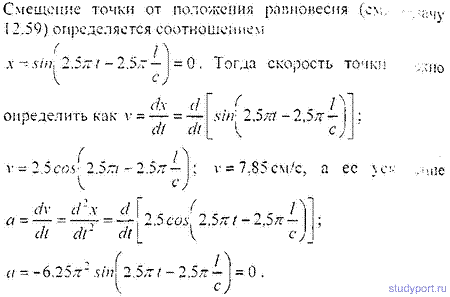Видео:Математические и пружинные маятники. 11 класс.Скачать
Математический маятник совершает затухающие колебания в соответствии с уравнением d2x dt2
2018-05-31 
Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания $lambda_ = 1,50$. Каким будет логарифмический декремент затухания, если сопротивление среды увеличить в $n = 2,00$ раза? Во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны?
По определению логарифмического декремента ($lambda = beta frac$) получаем исходный декремент $lambda_$
Для критического затухания $omega_ = n_ beta$
Видео:Урок 343. Затухающие колебания (часть 1)Скачать
Математический маятник совершает затухающие колебания в соответствии с уравнением d2x dt2
колебания и волны
Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания λ0 = 1,50. Каким будет логарифмический декремент затухания, если сопротивление среды увеличить в n = 2.00 раза? Во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны?
Дано:
Решение:
Коэффициент затухания β связан с логарифмическим декрементом затухания
Коэффициент затухания β
Период колебаний при затухающих колебаниях
Если сопротивление среды увеличить в n раз, то
Видео:математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать
Гармоническое колебательное движение и волны
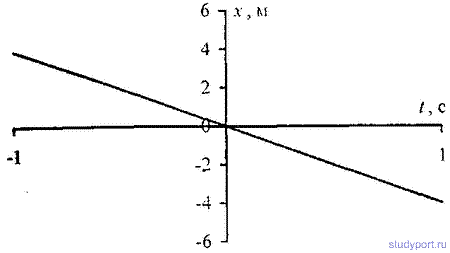
12.41. Точка участвует в двух взаимно перпендикулярных колебаниях x = sinPt и y = 2sin(Pt+P/2). Найти траекторию результирующего движения точки.
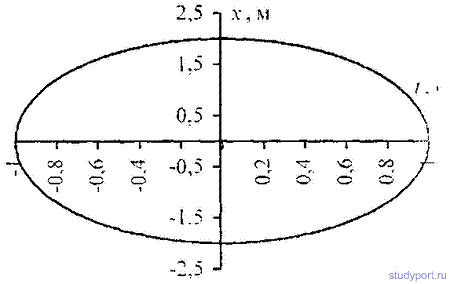
12 42. Точка участвует в двух взаимно перпендикулярных колебаниях х = sinPt a y = 4sin(Pt + P). Найти траекторию результирующего движения точки и начертить ее с нанесением масштаба.
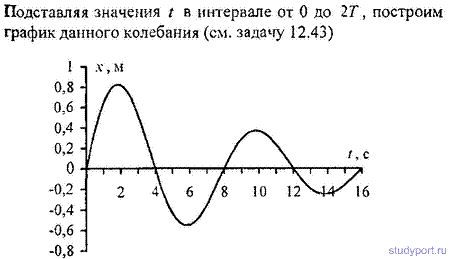
12.43. Период затухающих колебаний T = 4с; логарифмический декремент затухания N = 1.6; начальная фаза φ = 0. При t=T/4 смещение точки x = 4,5 см. Написать уравнение движения
этого колебания. Построить график этого колебания в пределах двух периодов.
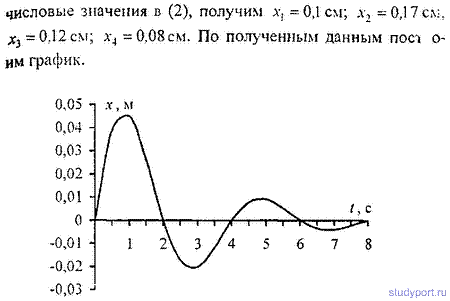
12.44. Построить график затухающего колебания, данного
уравнением x=5e -0,1t sinP/4t м.
12.45. Уравнение затухающих колебаний дано в виде x=5e -0,25t sinP/2tм. Найти скорость v колеблющейся точки в моменты времени t, равные: 0, T, 2T, 3Т и 4T,
12.46. Логарифмический декремент затухания математического маятника N = 0.2. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?
12.47. Найти логарифмический декремент затухания математического маятника, если за время t = 1мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника l= 1м.
12.48. Математический маятник длиной l = 24,7 см совершает затухающие колебания. Через какое время t энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания: а) N = 0,01; б) N = 1.
12.49. Математический маятник совершает затухающие колебания с логарифмическим декрементом затухания N = 0,2 . Во сколько раз уменьшится полное ускорение маятника в его крайнем положении за одно колебание?
12.50. Амплитуда затухающих колебаний математического маятника за время t = 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время t = 3 мин?
12.51. Математический маятник длиной l = 0,5м, выведенный из положения равновесия, отклонился при первом колебании на х1 = 5 см, а при втором ( в ту же сторону) — на x2 = 4см. Найти время релаксации t, т. е. время, в течение которого амплитуда колебаний уменьшится в е раз, где е — основание натуральных логарифмов.
12.52. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на dl = 9,8см. Оттягивая этот груз вниз и отпуская его, заставляют груз совершать колебания. Каким должен быть коэффициент затухания δ, чтобы: а) колебания прекратились через время t = 10 с (считать условно, что колебания прекратились, если их амплитуда упала до 1% от начальной); б) груз возвращается в положение равновесия апериодически; в) логарифмический декремент затухания колебаний был равным N = 6 ?
12.53. Тело массой m = 10 г совершает затухающие колебания с максимальной амплитудой Amax = 7см, начальной фазой φ = о и коэффициентом затухания δ = 1,6 см -1 . На это тело начала действовать внешняя периодическая сила F, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид х = 5sin(10Pt-3P/4) см. Найти (с числовыми коэффициентами) уравнение собственных колебаний и уравнение внешней периодической силы.
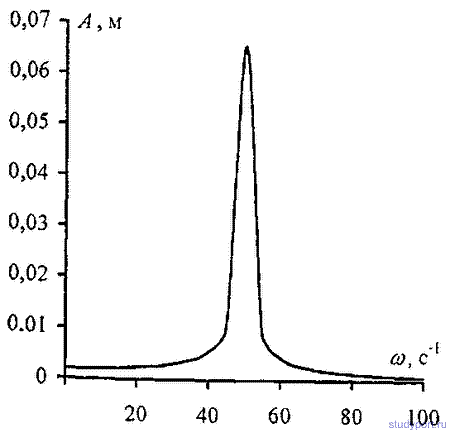
12.54. Гиря массой m = 0,2 кг, висящая на вертикальной пружине, совершает затухающие колебания с коэффициентом затухания δ= 0,75 см -1 . Жесткость пружины k = 0,5кН/м. Начертить зависимость амплитуды А вынужденных колебаний гирьки от частоты внешней периодической силы, если известно, что максимальное значение внешней силы F0 = 0,98 Н. Для построения .трафика найти значение А для частот: w= 0, w= 0,5, w = 0,75, w = w0, w = w=1,5w0 и w = 2w0, где w0— частота собственных колебаний подвешенной гири.
12.55. По грунтовой дороге прошел трактор, оставив следы в виде ряда углублений, находящихся на расстоянии l = 30 см друг от друга. По этой дороге покатили детскую коляску, имеющую две одинаковые рессоры, каждая из которых прогибается на x0 = 2 см под действием груза массой m0 = 1 кг. С какой скоростью v катили коляску, если от толчков на углублениях она, попав в резонанс, начала сильно раскачиваться? Масса коляски M= 10 кг.
12.56. Найти длину волны λ колебания, период которого T = 10 -14 с. Скорость распространения колебаний с = 3 * 10 8 м с.
12.57. Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду A =0.25 мм. распространяются в воздухе. Длина волны λ = 70 см. Найти скорость с распространения колебаний и максимальную скорость Vmax частиц воздуха.
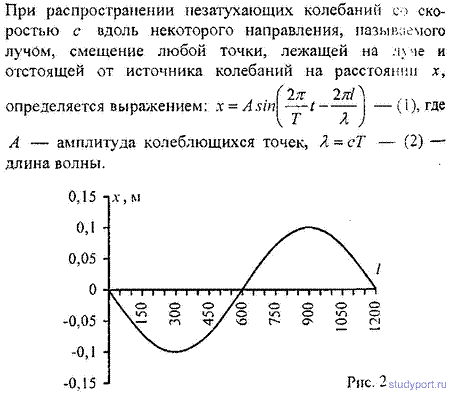
12.58. Уравнение незатухающих колебаний имеет вид
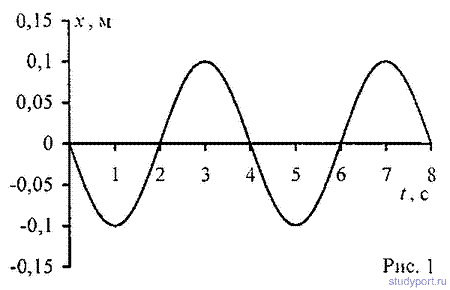
x=10sinP/2*t см. Найти уравнение волны, если скорость распространения колебаний с = 300м*с. Написать и изобразить графически уравнение колебания для точки, отстоящей на расстоянии
l = 600 м от источника колебаний. Написать и изобразить графически уравнение колебания для точек волны в момент времени t= 4 с после начала колебаний.
12.59. Уравнение незатухающих колебаний имеет вид x = 4sin600Pt см. Найти смещение x от положения равновесия
точки, находящейся на расстоянии l = 75 см от источника колебаний, для момента времени t = 0,01 с после начала колебаний. Скорость распространения колебаний с = 300 м/с.
12.60. Уравнение незатухающих колебаний имеет вид x=sin2,5Pt см. Найти смещение х от положения равновесия, скорость v и ускорение a точки, находящейся на расстоянии
l = 20м от источника колебаний, для момента времени t = 1с после начала колебаний. Скорость распространения колебаний с = 100 м*с.
Ошибка в тексте? Выдели её мышкой и нажми 
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
💥 Видео
МАТЕМАТИЧЕСКИЙ МАЯТНИК 😉 #егэ #математика #физик #shorts #огэСкачать
Видеоурок по физике "Математический и пружинный маятники"Скачать
Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать
Урок 92 (осн). Колебательное движение. МаятникиСкачать
Колебания математического маятникаСкачать
Период колебаний математического маятника 🧬 #shorts #умскул_физика #егэ2023 #егэфизикаСкачать
Математические и пружинные маятники. Практическая часть- решение задачи. 11 класс.Скачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Колебания математического и пружинного маятников. Практическая часть - решение задачи. 9 класс.Скачать
Поступающим в магистратуру МГУ, математика, 2018 год, первая волна, задача 1 (1)Скачать
Математический маятник - запись колебаний песком.Скачать
Лента Мёбиуса с Мэттом Паркером (фрагмент шоу "Четырехмерная математика")Скачать
9 класс, 34 урок, Колебания математического маятника и груза на пружинеСкачать
Физика 9 класс (Урок№10 - Маятник. Характеристики колебательного движения.)Скачать
Колебания математического и пружинного маятников. 9 класс.Скачать
Уравнения и графики механических гармонических колебаний. 11 класс.Скачать
Механические колебания. Математический маятник | Физика 11 класс #7 | ИнфоурокСкачать
