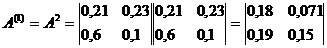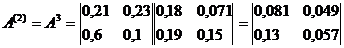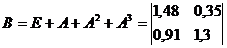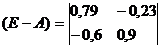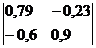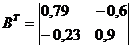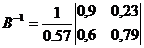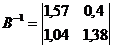Математически межотраслевой баланс описывается уравнениями

О планировании сказано достаточно. Независимо от нашего отношения к этому процессу, мы все время сталкиваемся с необходимостью сопоставлять свои силы со своими желаниями. И если в жизни одного-двух человек можно и ошибиться с планами, то на экономике государства, а то и целого союза держав, неверно соотнесенные затраты с прибылью могут сказаться катастрофически. Поэтому в современной экономике межотраслевой баланс со своей детализацией производства товаров и услуг занимает ведущее место.

Видео:Модель межотраслевого баланса. Часть 1 ТеорияСкачать

Балансовая модель – что это?

Экономико-математическое моделирование систем и производственных процессов активно использует так называемые балансовые модели, основанные на сопоставлении и оптимизации имеющихся ресурсов. С точки зрения математики, балансовый метод предполагает построение системы уравнений, которые описывают условия равенства между производимой продукцией и потребностью в этих товарах.

Исследуемая группа чаще всего состоит из нескольких экономических объектов, часть продукции которых потребляется внутри, а часть выводится за ее рамки и воспринимается как «конечный продукт». Балансовые модели, которые используют понятие «ресурс», а не «продукт», дают возможность управлять оптимальным расходованием ресурсов.

Видео:Григорий Копанев. Межотраслевой балансСкачать

Что дает модель

Метод межотраслевого баланса – один из важнейших элементов экономической аналитики. Он представляет собой матрицу коэффициентов, отражающих расходование ресурсов по заданным направлениям использования. Для проведения расчетов составляется таблица, ячейки которой заполняются нормативами прямых затрат на изготовление единицы продукции.

В силу сложности системы использовать реальные показатели какого-то одного предприятия не представляется возможным. Поэтому коэффициенты (нормативы) рассчитываются на так называемую «чистую отрасль», т. е. такую, которая объединяет все производственные предприятия без оглядки на ведомственную подчиненность или форму собственности. Это создает существенные проблемы при подготовке информационной составляющей для модели экономических систем.

Видео:Модель межотраслевого баланса. Часть 2 ПрактикаСкачать

Нобелевская премия за модель

Впервые о необходимости найти баланс производства между разными отраслями предложили советские экономисты, изучавшие статистические показатели развития народного хозяйства за 1923-1924 годы. Первые предложения содержали лишь информацию о качестве связей между производственными отраслями и об использовании произведенной продукции.

Но реального практического применения эти идеи не нашли. Спустя несколько лет экономист В. В. Леонтьев сформулировал важность межотраслевых связей в экономике. Его работа была посвящена созданию математической модели, позволявшей не только анализировать текущее состояние экономики государства, но и моделировать возможные сценарии развития.

Межотраслевой баланс получил в мире название метода «затраты-выпуск». А в 1973 году ученый был удостоен Нобелевской премии по экономике за разработку прикладной модели межотраслевого анализа.

Видео:Межотраслевой Баланс Продуктообмена (МОБ ПО) - Варианты учёта (§ 19.31)Скачать

Как использовалась модель

Впервые модель межотраслевого баланса Леонтьев применил для анализа состояния экономики США. К тому времени теоретические постулаты приобрели форму реальных линейных уравнений. Этот расчет показал, что коэффициенты, предложенные учеными в качестве показателей взаимосвязей между отраслями, достаточно стабильны и постоянны.

Во время Второй Мировой войны Леонтьевым был проанализирован межотраслевой баланс экономики гитлеровской Германии. По результатам этого исследования американские военные определили стратегически значимые цели. А по окончании войны качество и объем Ленд-лиза снова-таки определялся на базе информации, полученной через модель межотраслевого баланса Леонтьева.

В Советском Союзе такую модель строили 7 раз, начиная с 1959 года. Ученые предполагали, что на протяжении пяти лет экономические связи можно считать стабильными, поэтому и все условия считались статичными. Тем не менее, методика не получила широчайшего распространения, т. к. на взаимосвязи производственных отраслей в большей степени влияла политическая конъюнктура. Реальные же экономические связи рассматривались как второстепенные.

Видео:Модели межотраслевого балансаСкачать

Суть понятия

Модель межотраслевого баланса – это определение взаимосвязей между выпуском продукции в одной отрасли и затратами и потреблением товаров всех отраслей, задействованных в производстве этой продукции. Например, для добычи угля необходимы стальные инструменты; в то же время для выплавки стали нужен уголь. Так вот, задача межотраслевого баланса заключается в том, чтобы найти такое соотношение угля и стали, при котором экономический результат будет максимальным.

В более широком понимании можно говорить, что по результатам построенной модели можно определять эффективность производства вообще, находить оптимальные методы ценообразования и выявлять наиболее значимые факторы экономического роста. Кроме того, этот метод позволяет заниматься прогнозированием.

Видео:Экономист Леонтьев - Уравнение межотраслевого баланса - Возможность решения уравнения (§ 17.101)Скачать

Основные задачи

• Структуризация процессов воспроизводства, исходя из материально-вещественного состава отраслевых ресурсов.
• Иллюстрация процессов выпуска продукции и ее распределения.
• Детальное исследование производственного процесса, создания товаров и услуг, накопления доходов на уровне отраслей экономики.
• Оптимизация выявленных существенных факторов производства.

Для метода «затраты-выпуск» определены аналитическая и статистическая функции. Аналитическая позволяет прогнозировать динамические процессы развития отраслей и экономики в целом; моделировать ситуации, изменяя различные данные и показатели. Статистическая функция обеспечивает проверку согласованности информации, поступающей из различных источников – от предприятий, региональных бюджетов, налоговых служб и т. д.

Видео:Экономист Леонтьев - Уравнение межотраслевого баланса - Возможность решения уравнения (§ 17.11)Скачать

Математический вид модели

С точки зрения математики, балансовая модель – это система дифференцированных уравнений (и не всегда линейных), которые отображают условия равновесия между произведенной в отрасли совокупной продукцией и потребностью в ней.

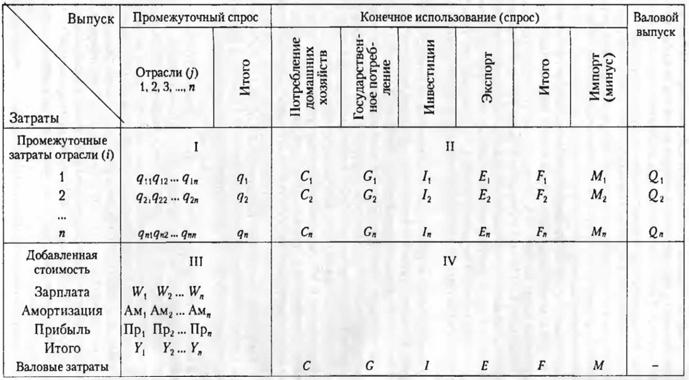
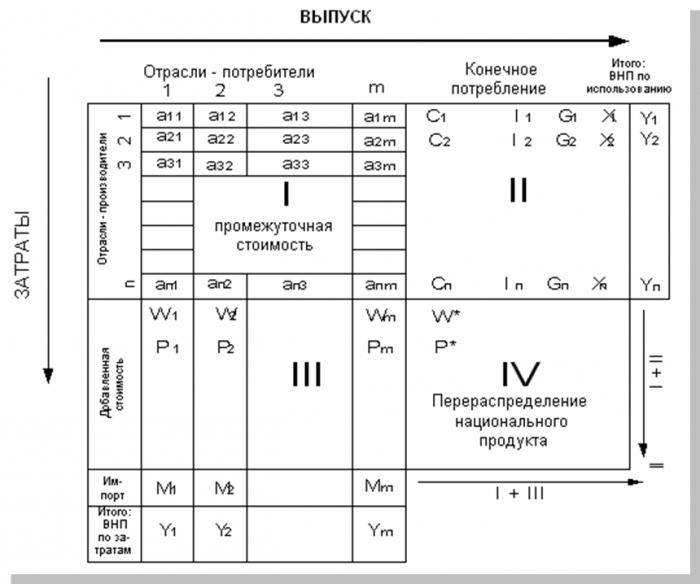
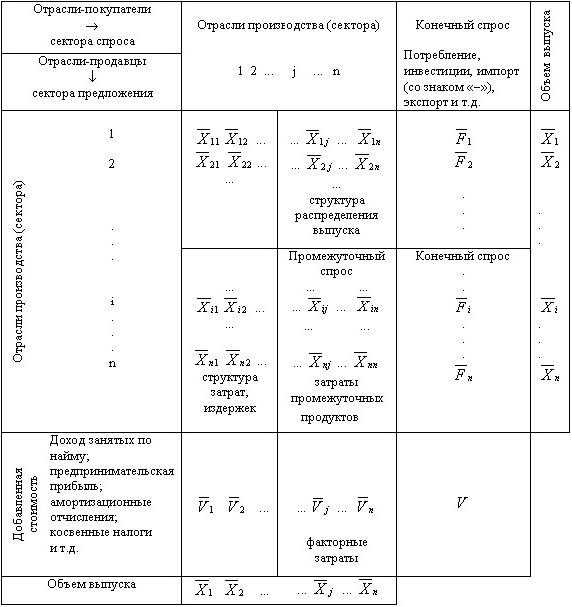
Модели экономических систем чаще всего представляются в виде таблицы (см. рис.). В ней совокупный продукт разделяется на 2 части: внутренний (промежуточный) и конечный. Народное хозяйство рассматривается как система из n чистых отраслей, каждая из которых выступает в роли производящей и потребляющей.

Видео:Модель Леонтьева "затраты-выпуск" в MS ExcelСкачать

Квадранты

Межотраслевой баланс Леонтьева разделен на четыре части (квадранта). Каждый квадрант (на рис. они обозначены цифрами 1-4) имеет свое экономическое содержание. В первом отображаются межотраслевые материальные связи – это своего рода шахматка. Коэффициенты, расположенные на пересечении строк и столбцов, обозначаются XY и содержат информацию о потоке продукции между отраслями. Х и Y – номера отраслей, которые производят и потребляют продукцию. Обозначение х23, например, следует трактовать так: стоимость средств производства, выпущенных в отрасли 2 и потребленных в отрасли 3 (материальные затраты). Сумма всех элементов первого квадранта представляет собой годовой фонд возмещения материальных затрат.

Второй квадрант представляет собой совокупность конечной продукции всех производственных отраслей. Конечным называется продукт, который выходит за рамки производственной сферы в область конечного потребления и накопления. Развернутая схема баланса иллюстрирует направления использования такого товара: общественное и личное потребление, накопление, возмещение и экспорт.

Третий квадрант описывает национальный доход. Он представляет собой сумму чистой продукции (оплата труда и чистый доход отраслей) и фонда возмещения. А в четвертом отображена информация о конечном распределении. Он находится на пересечении столбцов второго и строк третьего квадрантов. Эта информация необходима для понимания формирования системы доходов и расходов населения страны, источников финансирования, затрат непроизводственной сферы и т. д.

Отметим, что общий итог второго, третьего и четвертого квадрантов (каждого в отдельности) должен быть равен созданному за год продукту.

Видео:#shorts input output model leontief matrixСкачать

Система уравнений

Несмотря на то что валовый общественный продукт формально не входит в состав ни одной из вышеперечисленных частей, он все же присутствует в балансе. Столбец, который находится справа от второго квадранта, и строка, расположенная под третьим, отображают валовый общественный продукт. Информация, полученная из названных элементов, позволяет проверить правильность заполнения всего баланса. Кроме того, с ее помощью можно составить экономико-математическую модель.

Обозначив валовый продукт отрасли через Х с индексом, соответствующим номеру этой отрасли, можно сформулировать два основных соотношения. Экономический смысл первого уравнения сводится к следующему: сумма материальных затрат любой ветви хозяйства и ее чистой продукции равен валовому продукту описываемой отрасли (столбцы).

Второе уравнение межотраслевого баланса показывает, что сумма материальных затрат потребляющих какой-то товар и конечный продукт той или иной сферы представляют собой валовую продукцию отрасли (строки баланса).

Видео:Межотраслевой баланс системы коммунальной инфраструктуры и энергетикиСкачать

Конечный вид системы уравнений

С учетом всех названных формул, в модель вводятся такие понятия:

• матрица коэффициентов прямых затрат А = ;
• вектор валовой продукции Х (столбец);
• вектор конечной продукции У (столбец).

Модель в матричной форме будет описана соотношением:

Осталось только напомнить, что баланс составляется как в натуральных величинах, так и в денежном измерении.

Видео:Об оптимальном решении задачи Межотраслевого Баланса Продуктообмена (§ 19.60)Скачать

Примеры решений на тему «Межотраслевой баланс»

Отрасль

Потребление

Конечный продукт

Валовой выпуск

Производство

Решение проводим с помощью калькулятора.
По формуле a_ij = x_ij / x_j находим коэффициенты прямых затрат:

0.1

Коэффициент прямых затрат (a_ij) показывает, какое количество продукции i-й отрасли необходимо, учитывая только прямые затраты, для производства единицы продукции j-й отрасли.
Если ввести в рассмотрение матрицу коэффициентов прямых затрат A = (a_ij), вектор-столбец валовой продукции X = (X_i) и вектор-столбец конечной продукции Y = (Y_i), то математическая модель межотраслевого баланса примет вид:
X = AX +Y
Идея сбалансированности лежит в основе всякого рационального функционирования хозяйства. Суть ее в том, что все затраты должны компенсироваться доходами хозяйства. В основе создания балансовых моделей лежит балансовый метод – взаимное сопоставление имеющихся ресурсов и потребностей в них.
Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.
Пусть экономика страны имеет n отраслей материального производства. Каждая отрасль выпускает некоторый продукт, часть которого потребляется другими отраслями (промежуточный продукт), а другая часть – идет на конечное потребление и накопление (конечный продукт).
Обозначим через X_i (i=1..n) валовый продукт i-й отрасли; x_ij – стоимость продукта, произведенного в i-й отрасли и потребленного в j-й отрасли для изготовления продукции стоимостью X_j; Y_i – конечный продукт i-й отрасли.
Критерии продуктивности матрицы А
Существует несколько критериев продуктивности матрицы А.
1. Матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы.
2. Для того чтобы обеспечить положительный конечный выпуск по всем отраслям необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
3. Определитель матрицы (E — A) не равен нулю, т.е. матрица (E- A) имеет обратную матрицу (E — A) -1 .
4. Наибольшее по модулю собственное значение матрицы А, т.е. решение уравнения |λE — A| = 0 строго меньше единицы.
5. Все главные миноры матрицы (E — A) порядка от 1 до n, положительны.

Матрица A имеет неотрицательные элементы и удовлетворяет критерию продуктивности (при любом j сумма элементов столбца ∑a_ij ≤ 1.
I. Определим матрицу коэффициентов полных материальных затрат приближенно, учитывая косвенные затраты до 2-го порядка включительно.
а) Матрица коэффициентов косвенных затрат 1-го порядка равна:

б) Матрица коэффициентов косвенных затрат 2-го порядка равна:

Матрица коэффициентов полных затрат приближенно равна:

II. Определим матрицу коэффициентов полных затрат точно с помощью формул обращения невырожденных матриц.
Коэффициент полных затрат (b_ij) показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.
Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства продукции.
а) Находим матрицу (E-A):

б) Вычисляем обратную матрицу (E-A) -1 :
Запишем матрицу в виде:

Главный определить
∆ = (0.79 • 0.9-(-0.6 • (-0.23))) = 0.57234043753495
Транспонированная матрица

Обратная матрица


Найдем величины валовой продукции двух отраслей

Для определения элементов первого квадранта материального межотраслевого баланса воспользуемся формулой x_ij = a_ij • X_j.
Составляющие третьего квадранта (условно-чистая продукция) находятся как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта.
Межотраслевой баланс состоит из четырех квадрантов (табл.). Первый квадрант отражает межотраслевые потоки продукции. Второй характеризует отраслевую материальную структуру национального дохода.
Третий представляет национальный доход как стоимость условно-чистой продукции (Z_j), равной сумме амортизации (c_j), оплаты труда (v_j) и чистого дохода j-й отрасли (m_j). Четвертый квадрант показывает конечное распределение и использование национального дохода.

Чистый доход

Валовый продукт

Видео:Как спрос и предложение задают ценыСкачать

Примеры заданий

1. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат A и вектор конечной продукции Y. Найти вектор валовой продукции, составить межотраслевой баланс.
Пример №1, Пример №2, Пример №3, Пример №4, Пример №5, Пример №6, Пример №7, Пример №8, Пример №9, Пример №10, Пример №11

2. Рассматривается двухотраслевая модель экономики. Даны матрица прямых затрат A и вектор конечной продукции Y. Найти следующее:

• Проверить продуктивность матрицы A;
• Вектор валового выпуска;
• Межотраслевые поставки;
• Записать схему межотраслевого баланса.

Скачать решение

3. В отчетном периоде имел место следующий баланс продукции (тыс. тонн). Рассчитайте коэффициенты прямых затрат, полных затрат и косвенных затрат первого порядка. Сделайте запись баланса в матричной форме.
Решение.

4. В отчетном году натуральный баланс продукции выглядел следующим образом ( в тыс. тонн). На основе данного баланса:

1. Составьте матрицу прямых затрат.
2. Составьте матрицу полных затрат.
3. Рассчитайте коэффициенты косвенных затрат первого и второго порядка.
4. Запишите баланс в матричной форме.
5. Рассчитайте объем валовой продукции, если конечное потребление составит: Y(140,120,280).

Скачать решение.

5. Два цеха предприятия выпускают продукцию двух видов: цех № 1 – продукцию В, цех № 2 – продукцию С. Часть производимой продукции направляется на внутреннее потребление, а остальная является конечным продуктом. Коэффициенты прямых затрат заданы матрицей. Реализация продукции В на сторону составляет по плану 600 тонн, а продукции С – 300 тонн. Составьте плановую модель выпуска продукции (валового и конечного продукта) с учетом внутреннего потребления. Результаты расчетов запишите в таблицу.
Решение.

6. Каждый из трех цехов предприятия выпускает один вид продукции (изделие 1, изделие 2 и изделие 3 соответственно), часть которой направляется на внутрипроизводственное потребление. Коэффициенты прямых затрат и плановые объемы реализации продукции на сторону заданы матрицами. Рассчитайте план выпуска каждого изделия. Результаты расчетов оформите в таблице.
Пример.

7. В таблице приведены данные об исполнении баланса. Используя модель Леонтьева многоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной сохранится на прежнем уровне.
Решение.

Задание. Пусть экономика условно разделена только на две отрасли, межотраслевой баланс которых с указанием коэффициентов прямых материальных затрат и конечной продукции приведен в таблице. По этим данным рассчитать валовую продукцию каждой отрасли и межотраслевые поставки.
Решение. Скачать решение

Найти максимальный технологический рост и магистраль в динамической модели Леонтьева, задаваемой матрицей затрат
A = (1/2; 1/4
1/16; 1/2)

Видео:ЭТОТ метод поможет на уроках ХИМИИ / Химия 9 классСкачать

Межотраслевой баланс

Видео:04 Системы линейных уравненийСкачать

Межотраслевой баланс

Межотраслевой баланс (МОБ, модель «затраты-выпуск») — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Характеризует связи между выпуском продукции в одной отрасли и затратами продукции всех участвующих отраслей, необходимыми для обеспечения этого выпуска.

Рис.4 Межотраслевой баланс

Представляет собой систему линейных уравнений, таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе. Таблица показывает структуру затрат на производство каждого производимого продукта и структуру его распределения в экономике. По столбцам отражается состав продукции по элементам промежуточного потребления. По строкам отражаются виды конечной продукции.

Межотраслевой баланс является сердцем плановой экономики. С его помощью можно рассчитать план производства всей продукции, производимой экономикой. Он позволяет сбалансировать выпуск продукции в различных отраслях таким образом, чтобы количество произведенной продукции по каждой единице номенклатуры было достаточным для обеспечения всех нужд экономики и обеспечения выпуска продукта для конечного потребления в необходимом объеме.

Функциональные возможности системы ОГАС позволят обеспечить формирование единой таблицы МОБ всем видам продукции, производимым экономикой страны, а также обеспечить решение системы линейных уравнений МОБ, что даст возможность рассчитать план производства продукции по каждой единице номенклатуры и по каждому предприятию страны таким образом, чтобы покрыть все потребности экономики и обеспечить выпуск продукта для конечного потребления в нужном количестве.

Для формирования таблицы МОБ будут использоваться «цифровые двойники» продукции, которые будут формироваться каждым предприятием страны по каждому виду товаров и услуг, производимых предприятием. В этих «цифровых двойниках» будет содержаться информация о сырье, материалах, комплектующих, оборудовании и трудозатратах, применяемых при производстве каждой единицы номенклатуры товаров и услуг, производимых предприятием.

Поставив задание по необходимому количеству продуктов для конечного потребления с помощью таблицы межотраслевого баланса можно рассчитать валовый объем продукции, который необходимо произвести по каждому виду номенклатуры продукции на всех предприятиях страны.

Решение системы линейных уравнений МОБ является достаточно сложной вычислительной задачей, т.к. таблица МОБ в масштабах экономики страны может содержать десятки миллионов строк и столбцов. Решение такой сложной системы линейных уравнений широко известными математическими методами Жордана‑Гаусса или Крамера может потребовать настолько больших вычислительных ресурсов, что даже при нынешнем уровне развитии вычислительной техники они могут оказаться недостаточными для получения результатов планирования в сколько-нибудь приемлемые сроки.

Однако следует учитывать, что таблица МОБ является весьма разреженной, она будет состоять в основном из нулей, потому, что для производства любой продукции требуется ограниченное количество комплектующих и материалов, не сравнимое с общей номенклатурой продукции, производимой всей экономикой страны.

Поэтому решение такой разреженной системы линейных уравнений математическими методами Жордана-Гаусса или Крамера является неоптимальным с точки зрения затрат машинного времени.

Рекомендуется использовать другие, более подходящие в данном случае алгоритмы, оптимизированные для решения подобной системы линейных уравнений. В частности, можно использовать имеющийся в распоряжении автора данной концепции рекурсивный алгоритм, позволяющий решить подобную систему линейных уравнений с гораздо меньшим количеством операций и за гораздо меньшее время чем это позволяет сделать метод Жордана-Гаусса (при этом количество вычислений зависит от содержания данной системы уравнений и от необходимой точности конечного результата). Что делает задачу вычисления плана всей экономики страны с применением современных суперкомпьютеров за приемлемое время (минуты, часы) вполне реалистичной.

💡 Видео

Тихонов Н. А. - Методы математической физики - Классификация уравненийСкачать

Тихонов Н. А. - Основы математического моделирования - Типы математических моделей (Лекция 1)Скачать

Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минутСкачать

Модель ЛеонтьеваСкачать

Базовые модели математической биологии, представленные двумя автономными уравнениямиСкачать

Математика. Урок 1.8. Линейная алгебра. Модель Леонтьева многоотраслевой экономикиСкачать