Математическая модель представляет собой совокупность уравнений, неравенств, логических условий и других соотношений, отражающих взаимосвязи и взаимозависимости основных характеристик моделируемой системы.
По используемому математическому аппарату математические модели подразделяются на:
1) аналитические (описываемые с помощью систем уравнений, неравенств и т.д.);
2) статистические (реализующие выбор решения путем статистической обработки имеющихся решений).
Математическое моделирование — это изучение поведения объекта в тех или иных условиях путем решения уравнений его математичекой модели. У математически подобных объектов процессы обладают различной физической природой, но описываются идентичными уравнениями.
На первых порах своего развития математическое моделирование называлось аналоговым. Более того, использование метода аналогии привело к появлению аналоговых вычислительных машин — АВМ.
Общих методов построения математических моделей не существует. Работа над любой математической моделью начинается со сбора и анализа фактического материала. Определяются цели моделирования. Выделяются главные черты изучаемого объекта или явления. Вводятся формализованные характеристики. Принимаются правила работы с ними. В результате возникает математический объект, который и называется математической моделью.
Разрабатываются методы математического анализа модели, которыми она исследуется. Полученные результаты математического моделирования интерпретируются в рамках исходного фактического материала, что позволяет оценить степень адекватности модели. Результаты моделирования не должны противоречить выделенным








Предпочтение отдается более простым моделям. Отметим, что «простота» (иногда в ущерб точности) — один из принципов, о котором всегда нужно помнить при разработке математической модели.
Поскольку математическая модель не вытекает непосредственно из описания задачи, то одна и та же задача (одно и тоже явление) может иметь несколько моделей.
Построение модели в общем случае включает:
— составление математического описания;
— решение уравнений математического описания (аналитическое либо путем создания моделирующего алгоритма);
— проверку адекватности модели (это оценка достоверности построенной математической модели, исследование ее соответствия изучаемому объекту);
— окончательный выбор модели (при наличии нескольких моделей).
Требования к модели:
1. Затраты на создание и исследование модели должны быть значительно меньше затрат на создание и проведение эксперимента над оригиналом.
2. Модель должна отражать важнейшие черты явления (оригинала).
3. Модель должна быть, по возможности, простой, не «засоренной» массой мелких второстепенных деталей.
Компьютерное моделирование
Исторически случилось так, что первые работы по компьютерному моделированию, или, как говорили раньше, моделированию на ЭВМ, были связаны с физикой, где с помощью моделирования решался целый ряд задач гидравлики, фильтрации, теплопереноса и теплообмена, механики твердого тела и т. д. Моделирование, в основном, представляло собой решение сложных нелинейных задач математической физики с помощью итерационных схем, и по существу было оно моделированием математическим. Успехи математического моделирования в физике способствовали распространению его на задачи химии, элект-
роэнергетики, биологии и некоторые другие дисциплины, причем схемы моделирования не слишком отличались друг от друга. Сложность решаемых на основе моделирования задач всегда ограничивалась лишь мощностью имеющихся ЭВМ.
В настоящее время понятие «компьютерное моделирование» обычно связывают с системным анализом — направлением кибернетики, впервые заявившим о себе в начале 50-х годов при исследовании сложных систем в биологии, макроэкономике, при создании автоматизированных экономико-организационных систем управления. Основные методы и процедуры, используемые обычно при системном анализе, заимствованы из других дисциплин, в большей степени из исследования операций.
В настоящее время под компьютерной модельючаще всего понимают:
— условный образ объекта или некоторой системы объек
тов (или процессов), описанный с помощью взаимосвя
занных компьютерных таблиц, блоков-схем, диаграмм,
графиков, рисунков, анимационных фрагментов, гипер
текстов и т. д. и отображающий структуру и взаимо
связи между элементами объекта. Компьютерные мо
дели такого вида мы будем называть структурно-функ
циональными;
— отдельную программу, совокупность программ, про
граммный комплекс, позволяющий с помощью после
довательности вычислений и графического отображе
ния их результатов воспроизводить (имитировать) про
цессы функционирования объекта, системы объектов
при условии воздействия на объект различных, как
правило, случайных факторов. Такие модели мы бу
дем далее называть имитационными моделями.
Компьютерное моделирование — метод решения за
дачи анализа или синтеза сложной системы на основе
использования ее компьютерной модели. Суть компьютер
ного моделирования заключена в получении количествен
ных и качественных результатов по имеющейся модели.
Качественные выводы, получаемые по результатам ана
лиза, позволяют обнаружить неизвестные ранее свойства







Предметом компьютерного моделирования могут быть: экономическая деятельность фирмы или банка, промышленное предприятие, информационно-вычислительная сеть, технологический процесс, любой реальный объект или процесс, например, процесс инфляции, и вообще любая сложная система.
Компьютерная модель сложной системы должна, по возможности, отображать все основные факторы и взаимосвязи, характеризующие реальные ситуации, критерии и ограничения. Модель должна быть достаточно универсальной, чтобы по возможности описывать близкие по назначению объекты, и в то же время достаточно простой, чтобы позволить выполнить необходимые исследования с разумными затратами.
Исследование на компьютере
Видео:9 класс, 4 урок, Совокупности неравенствСкачать

Статья «Уравнения и неравенства как математические модели»
Математическая статистика − наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании). Любой творчески работающий специалист физического воспитания в ходе своей работы получают фактический экспериментальный материал (первичный цифровой массив). Если эти данные не будут корректно обработаны с помощью методов математической статистики, то их работа теряет всякий теоретический и практический смысл.
Просмотр содержимого документа
«Статья «Уравнения и неравенства как математические модели»»
уравнения и неравенства как математические модели
1.Примеры решения уравнений с параметрами как математической модели………………………………………………………………………..
1.1.Вид соотношений с выделенными параметрами……………………
1.2. Пример решения неравенства с параметром…………………….
Математическая статистика − наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании). Любой творчески работающий специалист физического воспитания в ходе своей работы получают фактический экспериментальный материал (первичный цифровой массив). Если эти данные не будут корректно обработаны с помощью методов математической статистики, то их работа теряет всякий теоретический и практический смысл.
В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, неравенств и их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.
Цель: проанализировать уравнения и неравенства как математические модели.
Провести теоретический анализ литературы по теме исследования.
примеры решения уравнений с параметрами как математической модели;
вид соотношений с выделенными параметрами;
пример решения неравенства с параметром.
1.Примеры решения уравнений с параметрами как математической модели
Ряд проблем в различных отраслях человеческой деятельности может быть изучен математическими методами. На этом пути, применяя язык математики, изучаемым явлениям ставят в соответствие модельные явления. Если они описаны с помощью математических правил, то такие модели называются математическими. Примером такого процесса является процесс решения простейших так называемых «текстовых» задач с помощью сведения их к уравнениям или неравенствам [7].
Любая предметная область характеризуется своим набором понятий связей между ними. Каждая предметная область имеет свои специфические методы решения задач. Необходимость в формализованном представлении знаний возникла в связи с их обработкой средствами компьютерной техники. Методология моделирования и формализации концептуальных знаний, ориентированная на их компьютерную обработку, является одной из основных тем развития искусственного интеллекта [7].
Под моделью мы будем понимать «систему произвольной природы, отражающую свойства, характеристики и связи моделируемого объекта (объекта-оригинала), которые считаются существенными для решения данной задачи» [5, с. 46]. При этом отсутствие в модели несущественных элементов не менее важно, чем присутствие в ней существенных.
Главное назначение модели состоит в упрощении получения информации о свойствах объекта-оригинала. Полное соответствие модели оригиналу невозможно по определению.
Пример. Рассмотрим уравнение 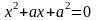
Множество решений такого уравнения – это множество пар чисел, при подстановке которых в уравнение получается верное равенство.
Взгляд относительно х говорит о решении уравнения относительно х. В этом случае аргументы х и а считают неравноправными. Поэтому необходимо выразить при решении х через а, которое называют «параметром».
Можно рассмотреть это уравнение по-другому, взгляд относительно а: необходимо иметь ответ в таком виде, чтобы для каждого значения а было указано, какие числа х в паре с этом а дают решения данного уравнения.
На этом пути, если брать разные основания для классификаций (например, от вида математического выражения, задающего уравнение) и учитывая разные взгляды на аргументы, входящие в это математическое выражение, получим спектр разных типов уравнений (неравенств).
1.1.Вид соотношений с выделенными параметрами
В реальных задачах (например, с физическим содержанием) естественно вводится неравноправие аргументов, входящих в уравнение. Они делятся на «неизвестные», обозначаемые, как правило, последними буквами латинского алфавита (…, x, y, z), и «параметры» – обозначаемые первыми буквами (a, b, c,…) [7].
Рассмотрим один из способов решения задачи с параметрами:
значение параметра (или параметров, если их несколько) считается произвольно фиксированным, и затем ищется решение задачи так, как обычно обращаются с уравнениями и неравенствами с одним неизвестным.
Ответом должно быть перечисление решений для каждого допустимого значения параметра.
Например, ответ при решении неравенства 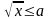
при 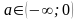
при 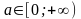
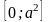
Отметим, что выяснение зависимости решений от значений параметра есть часть процесса решения задачи. Иногда это называют исследованием и отделяют от непосредственного решения. Необходимо запомнить и уяснить, что решение задачи с параметрами без такого этапа не дает решение. Задача нерешена!
1.2.Пример решения неравенства с параметром
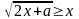
Решение. 1) Находим естественную область определения. Это множество пар 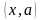
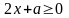

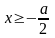
2) Так как 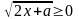
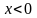
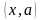
3) Рассмотрим случай 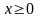
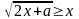

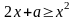

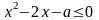
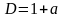
3.1. При 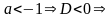
3.2. При 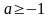
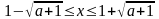
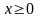
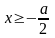
б) первое число больше второго .
Получаем два случая: и .
3.2.1) Пусть . В этом случае из трех исходных чисел самым большим является первое – число 0. Остаются условия 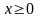
3.2.2) Пусть . Теперь первое число меньше второго и третьего. Сравним второе и третье: 

Это не выполняется ни при каких а. Итак, в этом случае третье число наибольшее. Получили, что 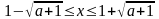
Ответ. 1) если , то решений нет;
2) если , то 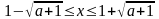
Как уже отмечалось, задачи с параметрами могут бать по-разному классифицированы:
по виду математического выражения (линейные, квадратные и т.д.);
по количеству неизвестных и выражений (системы и т.д.);
по количеству параметров [7].
Выделены и классы методов их решения (формальный, геометрический и др.).
Пример математической модели.
Производственное объединение, в которое входят две мебельные фабрики, нуждается в обновлении парка станков. Причем первой мебельной фабрике нужно заменить три станка, а второй-семь. Заказы можно разместить на двух станкостроительных заводах. Первый завод может изготовить не более 6 станков, а второй завод примет заказ если их будет не мение трех. Требуется определить как размещать заказы [8].
Введем переменные: xij-количество станков, которое будет изготавливать i-й завод для j-й фабрики.
По условию задачи:
Кроме того, должны выполняться условия:
Получаем систему ограничений в форме неравенств и уравнений:
Мы составили математическую модель нашей задачи. Решая систему мы найдем множество различных решений. Вот одно из них:
Оптимальное решение будет зависеть от других параметров, отдаленности заводов, цены на станки и т.д.
Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Электронная библиотека
Основным понятием курса является понятие математической модели. В общем случае слово «модель» – это отражение реального объекта. Такое отражение объекта может быть представлено схемой, эскизом, фотографией, моделью описательного характера в виде графиков, таблиц и т.д.
Математическая модель – это система математических уравнений, неравенств, формул и различных математических выражений, описывающих реальный объект, составляющие его характеристики и взаимосвязи между ними. Другими словами, математической моделью экономического объекта или процесса в общем случае называют совокупность соотношений (формул, уравнений, неравенств, логических условий и др.), определяющих выходные данные в зависимости от входных (параметров объекта, начальных условий, времени и пр.).
Математическая модель задачи представляет собой формальное описание основного содержания задачи. Процесс отображения основного содержания задачи (например, количественная связь между расходом ресурсов и имеющимися запасами их на складе предприятия через параметры управления) в виде математических формул, линейных уравнений, неравенств называется формализацией задачи.
Процесс построения математической модели называют математическим моделированием. Естественно, моделирование и построение математической модели экономического объекта позволяют свести экономический анализ производственных процессов к математическому анализу и принятию эффективных решений.
Поскольку нами изучаются экономические задачи, то и строятся экономико-математические модели, включающие:
ü выбор некоторого числа переменных величин для формализации модели объекта;
ü информационную базу данных объекта;
ü выражение взаимосвязей, характеризующих объект, в виде уравнений и неравенств;
ü выбор критерия эффективности и выражение его в виде математического соотношения – целевой функции.
Итак, для принятия эффективных решений в планировании и управлении производством необходимо экономическую сущность исследуемого экономического объекта формализовать экономико-математической моделью, т.е. экономическую задачу представить математически в виде уравнений, неравенств и целевой функции на экстремум (максимум или минимум) при выполнении всех условий на ограничения и переменные.
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
📹 Видео
Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Решение квадратных неравенств | МатематикаСкачать

Совокупность неравенств. Математика 7 класс. Подготовка к ЕГЭ, ОГЭ, ЦТ, экзаменамСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Неравенства с модулем | Математика | TutorOnlineСкачать

Математическая модель задачиСкачать

Уравнения с модулем. Часть 2 | Математика | TutorOnlineСкачать

Неравенства с модулем. Как правильно раскрывать модульСкачать

Как решить неравенства с модулем?Скачать

Русские vs американцы. Как решаем мы, а как они | МатематикаСкачать

9 класс, 14 урок, Системы уравнений как математические модели реальных ситуацийСкачать

7 класс, 3 урок, Что такое математическая модельСкачать

НЕРАВЕНСТВА С МОДУЛЕМСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Как распознать талантливого математикаСкачать

Алгебра 9 класс. Системы уравнений как математические модели реальных ситуацийСкачать

11 класс, 29 урок, Уравнения и неравенства с модулямиСкачать

МОДУЛЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать


