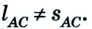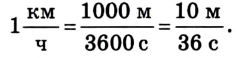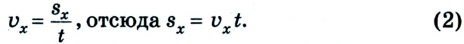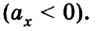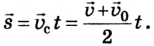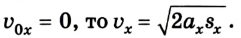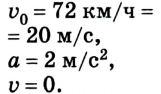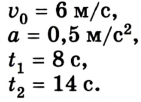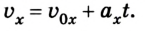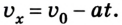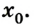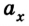Понятие «движение» определить не так уж просто, как это может показаться. С житейской точки зрения, это состояние является полной противоположностью покоя, но современная физика считает, что это не совсем так. В философии под движением подразумеваются любые изменения, происходящие с материей. Аристотель полагал, что данное явление равносильно самой жизни. А для математика любое перемещение тела выражается уравнением движения, записанным при помощи переменных и цифр.
- Материальная точка
- Основные понятия
- Равномерное движение по прямой
- Относительность движения
- Пример составления уравнений
- Если скорость отрицательна
- Движение с увеличением скорости
- Если ускорение отрицательно
- Сложное движение
- Кинематика в физике — основные понятия, формулы и определения с примерами
- Кинематика
- Механическое движение и траектория движения
- Путь и перемещение
- Равномерное прямолинейное движение
- МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДВИЖЕНИЙ: СИНЕРГЕТИЧЕСКИЙ И КОГНИТИВИСТСКИЙ ПОДХОДЫ
- 🎬 Видео
Видео:8 класс, 28 урок, Рациональные уравнения как математические модели реальных ситуацийСкачать

Материальная точка
В физике перемещение различных тел в пространстве изучает раздел механики, именуемый кинематикой. Если размеры некоего объекта слишком малы в сравнении с расстоянием, которое ему приходится преодолевать вследствие его движения, то он рассматривается здесь как материальная точка. Примером тому может служить автомобиль, едущий по дороге из одного города в другой, птица, летящая в небе, а также многое другое. Подобная упрощенная модель удобна при написании уравнения движения точки, за которую принимается определённое тело.
Бывают и другие ситуации. Представим, что тот же автомобиль хозяин решил переместить с одного конца гаража в другой. Здесь изменение местоположения сравнимо с размерами объекта. Поэтому каждая из точек автомобиля будет иметь разные координаты, а сам он рассматривается как объёмное тело в пространстве.
Видео:Математическая модель задачиСкачать

Основные понятия
Следует учитывать, что для физика путь, пройденный определённым объектом, и перемещение – совсем не одно и то же, а эти слова не являются синонимами. Уяснить разницу между данными понятиями можно, рассмотрев движение самолёта в небе.
След, который он оставляет, наглядно показывает его траекторию, то есть линию. При этом путь представляет собой её длину и выражается в определённых единицах (к примеру, в метрах). А перемещение – это вектор, соединяющий лишь точки начала и конца движения.
Подобное можно увидеть на рисунке, приведённом ниже, который демонстрирует маршрут машины, едущей по извилистой дороге, и вертолёта, летящего по прямой. Векторы перемещения для этих объектов будут одинаковые, а пути и траектории – разными.
Видео:Физика - уравнения равноускоренного движенияСкачать

Равномерное движение по прямой
Теперь рассмотрим различные виды уравнений движения. И начнём с самого простого случая, когда некий объект перемещается по прямой с одинаковой скоростью. Это значит, что по истечении равных промежутков времени путь, который он проходит за данный период, не меняется по величине.
Что нам потребуется для описания данного движения тела, вернее, материальной точки, как уже было условлено его называть? Важно выбрать систему координат. Для простоты предположим, что перемещение происходит вдоль некоей оси 0Х.
Тогда уравнение движения: x = х0 + vхt. Оно и будет описывать процесс в общем виде.
Важным понятием при изменении местоположения тела является скорость. В физике она является векторной величиной, поэтому принимает положительное и отрицательное значение. Здесь всё зависит от направления, ведь тело может перемещаться по выбранной оси с возрастающей координатой и в противоположную сторону.
Видео:7 класс, 3 урок, Что такое математическая модельСкачать

Относительность движения
Почему так важно выбрать систему координат, а также точку отсчёта для описания указанного процесса? Просто потому, что законы мироздания таковы, что без всего этого уравнение движения не будет иметь смысла. Это показано такими великими учёными, как Галилей, Ньютон и Эйнштейн. С начала жизни, находясь на Земле и интуитивно привыкнув выбирать её за систему отсчёта, человек ошибочно полагает, что существует покой, хотя для природы не бывает такого состояния. Тело может менять местоположение или оставаться статичным лишь относительно какого-либо объекта.
Мало того, тело может двигаться и находиться в покое одновременно. Примером тому может послужить чемодан пассажира поезда, который лежит на верхней полке купе. Он движется относительно деревни, мимо которой проезжает состав, и покоится по мнению своего хозяина, расположившегося на нижнем сидении у окна. Космическое тело, некогда получив начальную скорость, способно лететь в пространстве миллионы лет, пока не столкнётся с другим объектом. Движение его не будет прекращаться потому, что перемещается оно лишь относительно прочих тел, а в системе отсчёта, связанной с ним, космический путешественник находится в покое.
Видео:Тихонов Н. А. - Основы математического моделирования - Типы математических моделей (Лекция 1)Скачать

Пример составления уравнений
Итак, выберем за точку отсчёта некий пункт А, при этом координатной осью пусть будет для нас автомагистраль, находящаяся рядом. А направление её будет проходить с запада на восток. Предположим, что в эту же сторону в пункт В, расположенный за 300 км, пешком отправился путешественник со скоростью 4 км/ч.
Получается, что уравнение движения задаётся в виде: х = 4t, где t – время в пути. Согласно этой формуле, появляется возможность вычислить местонахождение пешехода в любой необходимый момент. Становится понятно, что через час он пройдёт 4 км, через два – 8 и достигнет пункта Б спустя 75 часов, так как его координата х = 300 окажется при t = 75.
Видео:УРОК 30. Моделирование движения тела в воздухе (11 класс)Скачать

Если скорость отрицательна
Предположим теперь, что из В в А едет автомобиль, имея скорость 80 км/час. Здесь уравнение движения имеет вид: х = 300 – 80t. Это действительно так, ведь х0 = 300, а v = -80. Следует обратить внимание, что скорость в данном случае указывается со знаком «минус», потому что объект перемещается в отрицательном направлении оси 0Х. Через какое время автомобиль достигнет пункта назначения? Это произойдёт, когда координата примет нулевое значение, то есть при х = 0.
Остаётся решить уравнение 0 = 300 – 80t. Получаем, что t = 3,75. Это означает, что автомобиль достигнет пункта В через 3 часа 45 минут.
Необходимо помнить, что координата тоже может быть отрицательной. В нашем случае это оказалось бы, если б существовал некий пункт С, находящийся в западном направлении от А.
Видео:Решение графических задач на равномерное движениеСкачать

Движение с увеличением скорости
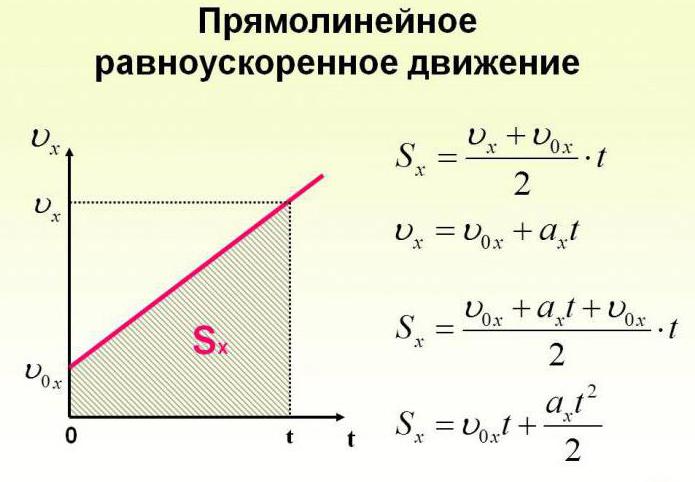
Перемещаться объект может не только с постоянной скоростью, но и менять её с течением времени. Движение тела может происходить по очень сложным законам. Но для простоты следует рассмотреть случай, когда ускорение увеличивается на определённое постоянное значение, а объект перемещается по прямой. В данном случае говорят, что это равноускоренное движение. Формулы, описывающие этот процесс, приведены ниже.
А теперь рассмотрим конкретные задачи. Допустим, что девочка, сев на санки на вершине горы, которую мы выберем за начало воображаемой системы координат с направлением оси по наклону вниз, начинает двигаться под действием силы тяжести с ускорением, равным 0,1 м/с 2 .
Тогда уравнение движения тела имеет вид: sx = 0,05t 2 .
Понимая это, можно узнать расстояние, которое девочка проедет на санках, для любого из моментов перемещения. Через 10 секунд это будет 5 м, а через 20 секунд после начала движения под гору путь составит 20 м.
Как выразить скорость на языке формул? Поскольку v0x = 0 (ведь санки начали катиться с горы без начальной скорости только под действием силы притяжения), то запись не будет слишком сложной.
Уравнение скорости движения примет вид: vx= 0,1t. Из него мы сможет узнать, как изменяется этот параметр с течением времени.
К примеру, через десять секунд vx= 1 м/с 2 , а через 20 с примет значение 2 м/с 2 .
Видео:Математическое моделирование - Лекция 1 (09.02.07)Скачать

Если ускорение отрицательно
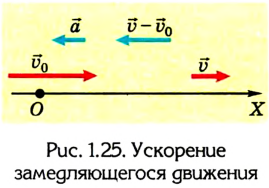
Существует и другой вид перемещения, относящийся к тому же типу. Это движение называют равнозамедленным. В данном случае скорость тела тоже изменяется, но с течение времени не увеличивается, а уменьшается, и тоже на постоянную величину. Снова приведём конкретный пример. Поезд, ехавший до этого с постоянной скоростью 20 м/с, начал тормозить. При этом ускорение его составило 0,4 м/с 2 . Для решения примем за начало отсчёта точку пути поезда, где он начал тормозить, а координатную ось направим по линии его перемещения.
Тогда становится понятно, что движение задано уравнением: sx = 20t — 0,2t 2 .
А скорость описывается выражением: vx = 20 – 0,4t. Необходимо заметить, что перед ускорением ставится знак «минус», так как поезд тормозит, и данная величина отрицательна. Из полученных уравнений возможно заключить, что состав остановится через 50 секунд, проехав при этом 500 м.
Видео:АУПО. Математическая модель продольного движения. ЛинеаризацияСкачать

Сложное движение
Для решения задач в физике обычно создаются упрощённые математические модели реальных ситуаций. Но многогранный мир и явления, происходящие в нём, далеко не всегда вписываются в подобные рамки. Как составить уравнение движения в сложных случаях? Проблема решаема, ведь любой запутанный процесс возможно описать поэтапно. Для пояснения снова приведём пример. Вообразим, что при запуске фейерверков одна из ракет, взлетевшая с земли с начальной скоростью 30 м/с, достигнув верхней точки своего полёта, разорвалась на две части. При этом соотношение масс получившихся осколков составило 2:1. Далее обе части ракеты продолжили двигаться отдельно одна от другой таким образом, что первая полетела вертикально вверх со скоростью 20 м/с, а вторая сразу упала вниз. Следует узнать: какова была скорость второй части в момент, когда она достигла земли?
Первым этапом данного процесса окажется полёт ракеты вертикально вверх с начальной скоростью. Перемещение будет равнозамедленным. При описании понятно, что уравнение движения тела имеет вид: sx = 30t – 5t 2 . Здесь мы полагаем, что ускорение свободного падения для удобства округляется до значения 10 м/с 2 . Скорость при этом будет описываться следующим выражением: v = 30 – 10t. По этим данным уже возможно вычислить, что высота подъёма составит 45 м.
Вторым этапом движения (в данном случае уже второго осколка) окажется свободное падение этого тела с начальной скоростью, получаемой в момент распадения ракеты на части. При этом процесс будет равноускоренным. Для нахождения окончательного ответа сначала вычисляет v0 из закона сохранения импульса. Массы тел относятся 2:1, а скорости находятся в обратной зависимости. Следовательно, второй осколок полетит вниз с v0 = 10 м/c, а уравнение скорости примет вид: v = 10 + 10t.
Время падения мы узнаем из уравнения движения sx = 10t + 5t 2 . Подставим уже полученное значение высоты подъёма. В результате выходит, что скорость второго осколка приблизительно равна 31,6 м/с 2 .
Таким образом, разделяя сложное движение на простые составные части, можно решать любые запутанные задачи и составлять уравнения движения всех видов.
Видео:2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

Кинематика в физике — основные понятия, формулы и определения с примерами
Содержание:
Основная задача механики — описание движения тел, т. е. выяснение закона (уравнения) их движения. Как отмечал А. Эйнштейн, наиболее фундаментальная проблема, остававшаяся нерешенной на протяжении тысячелетий, — это проблема движения. Собственно, учение о движении стало наукой лишь со времен Галилео Галилея и Исаака Ньютона.
Кинематика, изучает конкретные механические та их взаимодействия с другими телами. Она фактически объединяет простейшие пространственно-временные зависимости, в частности изменение координат тела со временем (как функцию времени).
Поэтому кинематику часто называют геометрией движения.
Кинематика изучает механические движения тел без учета их взаимодействия с другими телами.
Видео:Математическое моделированиеСкачать

Кинематика
Физика изучает разнообразные явления и процессы, происходящие вокруг нас. Как вам известно, в зависимости от их природы различают механические, тепловые, электрические, магнитные, световые и другие физические явления. Раздел физики, который объясняет движение и взаимодействие тел, называется механикой.
Слово «механика» впервые ввел Аристотель. Оно означает «машина».
Механика — одна из древнейших наук. Ее возникновение и развитие связано с практическими потребностями человека. Первые труды по механике, в которых рассматривались свойства простых механизмов и машин, появились еще в Древней Греции. Весомый вклад в ее становление сделали такие корифеи науки, как Аристотель (IV в. до н. э.), Архимед (III в. до н. э.), Леонардо да Винчи (XV в.), Галилео Галилей (XVII в.) и др. В завершенном виде как классическая теория она получила обоснование в работе Исаака Ньютона «Математические начала натуральной философии» (1687 г.). Современная механика, в основе которой лежит теория относительности, создана в начале XX в. Альбертом Эйнштейном.
Основная задача механики состоит в том, чтобы на основании параметров движения тела: координат, пройденного пути, перемещения, угла поворота, скорости, силы и т. д. — найти закон или уравнение, которое описывает это движение.
Основная задача механики состоит в том, чтобы найти уравнение движения тела с помощью параметров, описывающих это движение.
Т. е. если мы при помощи этих физических величин сможем установить положение тела в любой момент времени, то основная задача механики считается решенной. В зависимости от способов ее решения в механике выделяют три раздела: кинематика, динамика и статика.
Кинематика изучает, как движется тело, не вникая в причины, вызывающие именно такое движение. Поэтому кинематические уравнения состоят лишь из пространственных характеристик механического движения: пройденного пути, изменения координат тела, скорости и т. д. В них нет сил, изменяющих это движение.
В переводе с греческого слово кинематика» (kinematos) означает движение.
Механическое движение и траектория движения
Чаще всего в обыденной жизни мы наблюдаем явление, которое называется механическим движением. Например, автомобиль едет по дороге, в небе «плывут» тучи, ребенок катается на качелях, Луна вращается вокруг Земли и т. д. Во всех этих случаях происходит изменение положения одного тела или его частей относительно других. Чтобы убедиться в этом, необходимо выбрать тело отсчета, относительно которого можно фиксировать положение движущегося тела в любой момент времени. Тело отсчета выбирают произвольно. В приведенных примерах это может быть столб или дерево возле дороги, дом, поверхность Земли и т. д.
Для того чтобы описать движение тела, необходимо точно знать его местоположение в пространстве в произвольный момент времени, т. е. уметь определять изменение положения тела в пространстве относительно других тел с течением времени. Как известно, легче всего это можно сделать с помощью системы координат. Например, зафиксировать «адрес» тела как определенное его положение в пространстве, измерив расстояния или углы в некоторой системе координат.
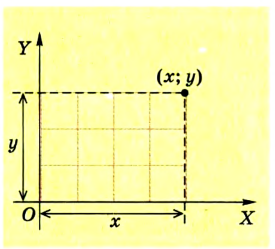
Например, в географии положение тела на земной поверхности задается двумя числами на пересечении меридиана и параллели, которые называются географической долготой и широтой. В математике «адрес» точки чаще всего определяют ее координатами, в частности в прямоугольной (декартовой) системе координат на плоскости — это расстояния х и у (рис. 1.1).
Взаимные изменения положения тела или его частей в пространстве с течением времени называются механическим движением.
Систему координат, как правило, связывают с телом отсчета. В данном случае движущееся тело характеризуется изменением положения в пространстве относительно тела отсчета, т. е. изменением его координат с течением времени.
Математически это можно записать в таком виде: х = x(t); у = y(t).
Для того чтобы определить такое изменение в любой момент времени, с телом отсчета и системой координат необходимо связать средство измерения времени, к примеру секундомер или хронометр. Тогда тело отсчета, связанную с ним систему координат и секундомер как единое целое называют системой отсчета.
Как известно, реальные физические тела имеют форму и объем. Поэтому однозначно задать их положение в пространстве не всегда представляется возможным, поскольку различные их части имеют разные координаты. Однако эту проблему можно упростить, если не брать во внимание размеры тела. Такое возможно лишь при определенных условиях.
Чтобы выяснить их, рассмотрим движение автомобиля. На значительных расстояниях, например на шоссе между Киевом и Харьковом, размерами автомобиля можно пренебречь, поскольку они значительно меньше расстояния между этими городами. Поэтому нет необходимости рассматривать особенности движения каждой части кузова автомобиля — достаточно его представить как движение точки.
Таким образом, для упрощения описания движения тел, когда их размерами при определенных условиях можно пренебречь, применяют понятие материальной точки. Это условное тело, не имеющее размеров, которое определяет положение реального тела в пространстве при помощи координат такой, материальной точки. Ее геометрический образ — невесомая точка, не имеющая размеров. В случае поступательного движения, при котором все точки тела движутся одинаково, любое тело можно считать материальной точкой.
Материальная точка — это физическая модель, при помощи которой представляют реальное тело, пренебрегая его размерами.
Часто кроме движущихся предметов мы наблюдаем тела, пребывающие в состоянии покоя. Однако абсолютно неподвижных тел в природе не существует.
Рассмотрим такой пример. В вагоне на столе стоит бутылка с водой (рис. 1.2). Во время движения поезда разные наблюдатели — пассажир в купе и провожающий на перроне — оценят ее состояние движения по-разному. Для сидящего пассажира она неподвижна, поскольку расстояние от него до бутылки не изменяется. Для провожающего на перроне 16 она движется, потому что изменяет свое положение с течением времени в системе отсчета, связанной с перроном.
Следовательно, состояние покоя является относительным, равно как и состояние движения, поскольку зависит от выбранной системы отсчета. Поэтому в дальнейшем при рассмотрении движения тела мы в первую очередь будем определяться с выбором системы отсчета, потому что от этого нередко зависит сложность уравнений, описывающих данное движение. Правильный выбор системы отсчета ведет к упрощению уравнений движения.
Состояние покоя и состояние движения тела относительны, поскольку зависят от выбора системы отсчета.
Рассмотрим движущееся тело, последовательно фиксируя его положение в определенные моменты времени. Если теперь соединить все точки, в которых побывало тело во время своего движения, то получим мнимую линию, которая называется траекторией движения. Траектория движения может быть видимой (след от самолета на небосклоне, линия от карандаша или ручки при записи в тетради) и невидимой (полет птички, движение теннисного мяча и т. д.).
По форме траектории механическое движение бывает прямолинейным и криволинейным (рис. 1.3).
Положение броуновской частички через определенные промежутки времени.
Рис. 1.3. Различные формы траектории
Траектория прямолинейного движения — прямая линия. Например, падение тела с определенной высоты или движение шарика по наклонному желобу. Во время криволинейного движения тело перемещается по произвольной кривой. Часто реальное движение тел является комбинацией прямолинейного и криволинейного движений. Например, комбинированным есть движение автобуса по маршруту: на разных участках траектория его движения может быть и прямолинейной, и криволинейной.
Поскольку движение тел происходит в определенных системах отсчета, то и траектория рассматривается относительно них. Ведь она отображает во времени последовательные положения тела в некоторой системе отсчета. Поэтому она будет отличаться формой в различных системах отсчета, т. е. траектории движения также относительны. Например, все точки колеса велосипеда относительно его оси описывают окружность, однако в системе отсчета, связанной с землей, эта линия более сложная (рис. 1.4).
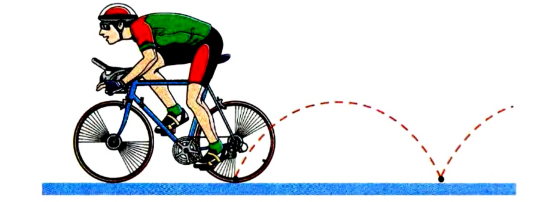
Рис. 1.4. Траектория движения точки обода колеса велосипеда
Путь и перемещение
Зная траекторию движения, можно определить путь, пройденный телом: для этого необходимо измерить длину траектории между начальной и конечной точками движения.
Путь — это длина траектории, которую проходит тело или материальная точка за определенный интервал времени. Он обозначается латинской буквой l. Данная физическая величина является скалярной и характеризуется лишь значением длины траектории движения.
В Международной системе единиц (СИ) путь измеряется в метрах (м). На практике используют также другие единицы пути — километр (км), сантиметр (см) и др.
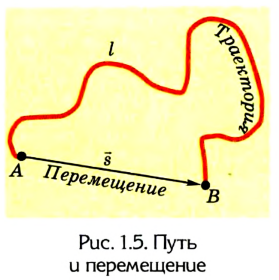
Часто, для того чтобы более полно охарактеризовать движение тела и найти его новое положение, кроме пройденного пути (длины траектории), необходимо указать также направление, в котором двигалось тело. Например, водителю автомобиля приходится ехать по извилистой дороге (рис. 1.5).
Пройденный путь — это длина дороги I, по которой ехал автомобиль. Водитель же совершил перемещение в пространстве из точки А в точку В, которое можно найти, соединив начальное и конечное положение тела прямой линией, указав при этом направление движения.
Следовательно, направленный отрезок прямой, соединяющий начальное положение движущегося тела с конечным, называется перемещением. Перемещение — это векторная величина. Оно обозначается латинской буквой 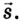
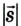
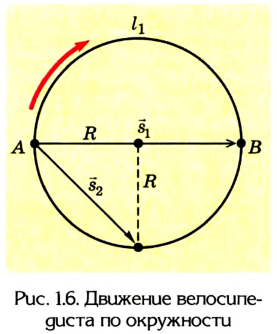
Путь и перемещение могут отличаться своими значениями. Чтобы убедиться в этом, рассмотрим движение велосипедиста по окружности радиуса R= 100 м (рис. 1.6).
Допустим велосипедист стартует в точке А. Проехав половину окружности, он окажется в точке В. Пройденный им путь равен дуге 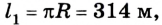
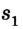
В момент времени, когда велосипедист проедет 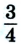
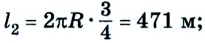
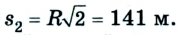
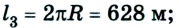
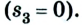
Путь и перемещение имеют также одинаковые значения, когда тело движется прямолинейно лишь в одном направлении.
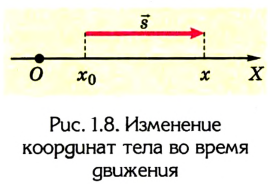
В рассмотренном нами примере пройденный путь и перемещение разные, отличаются по своему значению. Возникает вопрос: могут ли они совпадать, быть одинаковыми? Можно легко убедиться в том, что такое возможно, если, во-первых, траектория движения будет прямой, во-вторых, движение происходит в одну сторону. Как подтверждение этого, рассмотрим — такой пример.
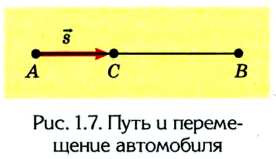
Допустим, что автомобиль движется прямолинейно по шоссе из пункта А в пункт В, а затем возвращается в пункт С. Расстояние между пунктами 2 км и 4 км соответственно, все они размещены на одной прямой (рис. 1.7).
Двигаясь из пункта А в пункт В, автомобиль проходит путь 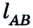
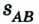
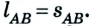
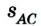
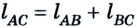
Следовательно, пройденный путь и перемещение по своему значению одинаковы лишь в том случае, если тело движется по прямой и не изменяет направление движения.
Равномерное прямолинейное движение
Простейшим видом механического движения является равномерное прямолинейное движение. Это такое движение, при котором тело, двигаясь по прямой, за любые одинаковые интервалы времени совершает одинаковые перемещения. Его траектория — прямая линия. Поэтому его можно описать переменой одной из координат, например х = x(t), если координатная ось совпадает с направлением движения.
Пусть тело в начальный момент движения имеет координату 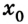
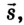
Как известно, в СИ скорость
измеряется в метрах за секунду (м/с). 1 м/с — это скорость такого равномерного прямолинейного движения, при которой тело за 1 с совершает перемещение 1 м. На практике используют также другие единицы скорости, например километр в час:
Поскольку перемещение 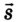
При равномерном движении значение скорости остается постоянным, поскольку за любые равные интервалы времени совершаются равные перемещения.
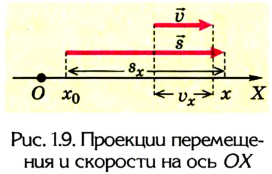
Как известно, основной задачей механики является определение положения тела в пространстве в произвольный момент времени. Следовательно, чтобы ее решить, надо найти координаты тела либо их изменение во времени: х — x(t). В механике такое уравнение называется уравнением движения. При решении задач с использованием уравнения движения векторные величины, характеризующие движение тела, записывают в проекциях на соответствующую ось. Следовательно, из формулы (1) получаем:
Из рисунков 1.8 и 1.9 понятно, что 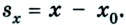
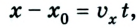

Уравнения равномерного прямолинейного движения:
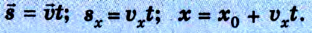
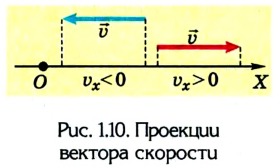
Рассмотрим теперь различные случаи равномерного прямолинейного движения (рис. 1.10).
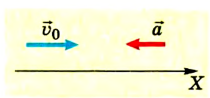
Из рисунка следует, что если направление движения тела совпадает с направлением координатной оси, то 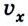
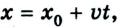
Если же направление движения тела противоположно направлению координатной оси, то 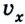
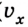
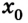
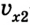
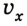
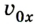
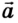
Если скорость тела со временем уменьшается 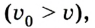
В данном случае в соответствии с выбранным направлением координатной оси ОХ проекция ускорения будет отрицательной
Вместе с тем знак проекции ускорения не определяет характер движения — оно ускоряющееся или замедляющееся, в зависимости от выбора системы отсчета. В этом легко убедиться, если рассмотреть случай, когда оба тела движутся в противоположных направлениях. Тогда одно из тел имеет положительную проекцию ускорения 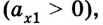
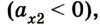
Из формул (1) и (2) можно получить кинематическое уравнение скорости для равноускоренного движения:

или в проекциях на ось ОХ:
Выведем теперь кинематическое уравнение перемещения для равноускоренного движения. Учтем, что скорость во время такого движения постоянно изменяется, например сначала она равна 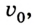
Подставив в данную формулу уравнение (3) и произведя некоторые преобразования, получим: 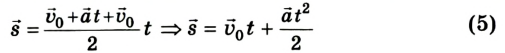
или в проекциях на ось ОХ: 
Если начальная скорость тела равна 0 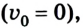

или в проекциях на ось ОХ: 
Для прямолинейного движения, учитывая, что 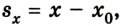
или для случая, когда 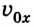

Следует помнить, что в ходе решения задач необходимо учитывать знаки проекций в соответствующих уравнениях.
При определении проекции перемещения не всегда известно время, в течение которого происходило движение. Тогда можно воспользоваться иным уравнением. Чтобы его получить, подставим в кинематическое уравнение 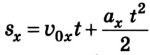
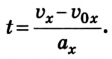

Отсюда 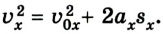
Задача №5
Водитель начинает тормозить в тот момент, когда спидометр автомобиля фиксирует скорость 72 км/ч. Через какое время автомобиль остановится, если он двигался с ускорением 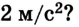
Дано:
По условию задачи спидометр показывает начальную скорость автомобиля 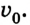
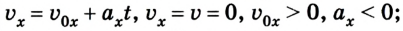
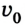
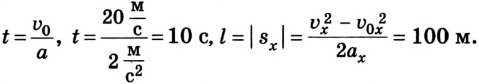
Ответ: автомобиль остановился через 10 с, проехав 100 м.
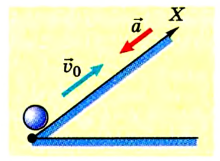
Задача №6
Шарик толкнули по наклонному желобу вверх со скоростью 6 м/с. Шарик движется с ускорением 0,5 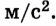
Дано:
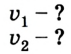
Решение
Направим ось ОХ вдоль желоба (см. рис.).
Учитывая знаки проекций скорости и ускорения, имеем
Отсюда уравнение для 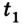
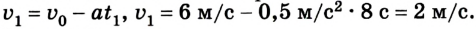
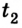
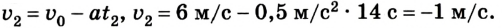
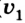
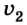
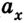
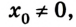
Если 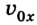
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика 5 класс. Математическая модельСкачать

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДВИЖЕНИЙ: СИНЕРГЕТИЧЕСКИЙ И КОГНИТИВИСТСКИЙ ПОДХОДЫ
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДВИЖЕНИЙ: СИНЕРГЕТИЧЕСКИЙ И КОГНИТИВИСТСКИЙ ПОДХОДЫ
Психологи, исследующие движения, не удовлетворяются их чисто качественным описанием и активно используют математические методы для описания и моделирования двигательных актов. Стремление к построению количественных, математических моделей человеческого движения вполне обосновано и выражает глубокую потребность в разработке предсказательного, а не только констатирующего описания. Немалую роль в этом отношении сыграли и чисто практические потребности, связанные, например, с изучением человека как исполнительного звена системы «человек машина » и приведшие к пополнению математического арсенала психологии идеями теории линейных систем и теории оптимального управления, используемых при описании машинной части этой системы.
Казалось бы, в этом отношении двигательная функция, сравнительно с другими психическими функциями, представляет чуть ли не идеальный объект. В отличие от лишенных непосредственных внешних проявлений процессов памяти или внимания, о которых приходится судить лишь на основании косвенных данных, движение непосредственно наблюдаемо, его траекторию легко зарегистрировать, и ничто не мешает подвергнуть ее сколь угодно детальному анализу.
Между тем количественное описание движений оказалось исключительно трудной задачей. Движение упрямо не желало укладываться в рамки какоголибо единого универсального закона или механизма, активно сопротивлялось навязанной извне формализации.
Фундаментальные исследования Н.А. Бернштейна, составившие целую эпоху в науке о движении, привели к пониманию движения как принципиально функционального образования, характеризуемого уровневой структурой и кольцевым характером процесса управления. На вершину иерархии уровней Н.А. Бернштейн поставил уровень действия. Эмпирические свойства этого уровня таковы, что логически необходимым оказалось постулировать «модель потребного будущего «, без которой невозможно понять активный характер действия. Таким образом, именно уровень действия оказался основным предметом собственно психологического исследования. Стало понятно, что неудачи в поиске детерминистических количественных законов человеческого движения связаны не столько с недостающими знаниями о телесной структуре, сколько прежде всего с отсутствием адекватных способов математического описания действия.
Надо сказать, что Н.А. Бернштейн очень осторожно, даже деликатно привлекал средства математики для описания движения, всякий раз подбирая такие методы, которые были бы наиболее адекватны рассматриваемому уровню движения. Так, описывая динамику кинематических цепей человеческого тела, он опирался на аппарат дифференциальных уравнений, т.е. использовал методы классической механики. Частотнофазовый анализ траекторий движения (ряды Фурье) был использован им при рассмотрении простейших афферентных синтезов (уровни А, В), репертуар которых изобилует почти синусоидальными периодическими движениями. Кибернетический подход был использован при рассмотрении механизма управления движениями в кольцевой схеме (1961). Наконец, наряду с другими альтернативами в последних
работах (1966) были рассмотрены представления о волновых процессах в тканях мозга и математика операторов (т.е. абстрактных правил преобразования) как наиболее адекватная процессам высших синтезов, осуществляемых в ЦНС.
Оформившееся немногим более десяти лет назад синергетическое направление предлагает свой вариант построения количественной теории движений. К используемому синергетикой математическому аппарату следует подходить столь же осторожно, т.е. прежде всего необходимо выяснить, какие именно уровни построения движения этот аппарат описывает и в какой мере он способен описать уровень действия, особенно интересный психологу.
До обсуждения синергетического подхода к движению полезно, как нам кажется, подчеркнуть те ключевые позиции, с которых рассматривается движение в когнитивной психологии. Это представляется тем более важным, что синергетический подход исторически возник как альтернатива когнитивизму. Кроме того, мы предполагаем, что для количественного описания движений можно использовать математику операторов, основываясь на принципиальных положениях теории Н.А. Бернштейна и учитывая ряд принципиальных положений когнитивизма и синергетики.
КОГНИТИВИСТСКИЙ ПОДХОД К МОДЕЛИРОВАНИЮ ДВИЖЕНИЙ
Как известно, центральными понятиями когнитивной психологии являются понятие внутренней репрезентации, т.е. структурно организованного знания (информации), и понятие процедуры преобразования информации. Если попытаться кратко сформулировать суть когнитивистского подхода к моделированию движений, то он сводится к попытке объяснения и предсказания свойств движений посредством моделирования структуры соответствующих этим движениям моторных программ. При этом вопрос о том, откуда и как возникают сами программы, остается вне проблемы моделирования предполагается, что программы как-то формируются в ходе двигательного научения.
Не претендуя на исчерпывающий анализ проблемы, ограничимся здесь лишь перечислением нескольких характерных черт когнитивистского подхода к математическому моделированию движений и логических трудностей, проистекающих из этих черт.
Одно из следствий сведения проблемы управления движениями к проблеме структуры моторной программы состоит в том, что любой процесс, происходящий в моторных программах, рассматривается как определенная последовательность преобразования и передачи управляющей информации от одного структурного блока программы к другому, т.е. как некий алгоритм. Это приводит к тому, что в рамках когнитивистского подхода преобладают модели главным образом лишь хорошо выученных, стереотипных движений, управляемых по «открытому контуру управления «. Такая тенденция вполне объяснима, поскольку лишь в этом случае имеет смысл говорить о структуре моторной программы и соответствующем ей алгоритме, в то время как существенно адаптивному процессу двигательного научения, когда результат движения влияет на способ его дальнейшего выполнения, трудно поставить в соответствие какуюлибо определенную структуру. Если все же рассматривают модели таких движений, которые адаптивны по своей сути (движение к цели, слежение), то и эти движения представляют в виде многократного выполнения одной и той же микропрограммы, пытаясь таким образом понять адаптивную изменчивость движения как последовательность неадаптивных по своей сути элементов.
Нередко принцип построения моторной программы напрямую заимствуется из наблюдаемых свойств движения. Так, если движение регулярно повторяется во времени, то предполагают, что и управляющий им механизм должен содержать соответствующий «источник » периодического сигнала; если движение обнаруживает черты регулярности в пространстве, то в качестве его внутренней репрезентации рассматривается пространственный шаблон, обладающий регулярностью во «внутреннем пространстве «. Кстати, именно эта
тенденция строить внутреннюю репрезентацию движений, исходя из принципов их внешней пространственновременной упорядоченности, послужила причиной того, что когнитивизм упрекают в бесконечном объяснительном регрессе. Опасность некритического уподобления характера внутренних процессов наблюдаемым свойствам движения подчеркивал и Н.А. Бернштейн [2].
Представление моторной программы в виде структуры взаимодействующих функциональных блоков, преобразующих информацию, неизбежно связано с предположением о том, что каждый из этих блоков обладает всей полнотой знания о том, как именно и когда преобразовывать информацию, поступающую на его вход. Поэтому когнитивистский подход вынужден постоянно опираться на предположение о наличии необходимого «процедурного знания «, происхождение и структура которого остаются нераскрытыми в рамках этого теоретического направления.
Наконец, отметим, что в построенном когнитивизмом мире исключительно целесообразного преобразования информации всякая вариативность рассматривается как фактор безусловно вредный, как «шум » или «помеха «. Неизменное присутствие вариативности обычно относят на счет несовершенства биологических систем. Для выявления «очищенных от шумов » закономерностей движения привлекается статистический подход при анализе экспериментальных данных и, соответственно, вероятностные методы при математическом моделировании движений.
Отмеченные выше черты когнитивистского подхода несложно проследить на ряде примеров. Здесь мы рассмотрим ритмические движения и движения к цели два относительно простых и в то же время фундаментальных класса движений [16].
Временную структуру быстрых автоматизированных ритмических движений часто объясняют [10], [19], [20] взаимодействием модальнонеспецифического центрального таймера и подчиненной ему пассивной моторной системы, отвечающей заданным движением на каждый импульс таймера. Временной рисунок движения и его темп целиком определяются структурой таймера, о которой судят по ковариационным взаимосвязям между вариативностью темпа центрального таймера и вариативными же задержками, происходящими в моторной системе. Основной результат этого направления представление об иерархической организации таймера, т.е. представление его как иерархии (или гетерархии) запускающих друг друга элементарных таймеров (например, [19]).
Нетрудно заметить, что проблема ритмической организации движений сводится в этом случае к определению структуры центрального таймера внутреннего «генератора ритмов «. Поскольку природа этого гипотетического образования остается неизвестной, возникает целый ряд характерных для когнитивизма трудностей. Так, возникает вопрос, каким именно образом структура центрального таймера и его темп всякий раз сообразуются с наличной двигательной задачей. В частности, чем именно определяется предельно быстрый темп выполнения ритмического движения? Если биомеханическими ограничениями, то каким образом независимый от моторной системы таймер «узнает » об этом? Если предельным темпом самого таймера, то чем определяется этот предел? Ответить на эти вопросы можно лишь при условии, что известна природа самого таймера, включая характер процесса его формирования.
Другое направление в моделировании структуры программ ритмических движений исходит из того, что временная структура ритмического движения определяется непосредственно структурой моторной программы, которая, в свою очередь, зависит от количества, характера и последовательности движений в повторяющемся фрагменте ритма. Такова модель иерархического устройства моторной программы ритмических движений (а также и более широкого класса дискретных серийных движений), предложенная Д. Розенбаумом и его коллегами [14], [15] и носящая название «treetraversal model «.
Рис. 1. Возможная структура альтернативных бимануальных ритмических движений
с точки зрения иерархической модели ритмических движений (treetraversal model)
В качестве примера применим эту модель к случаю быстрых попеременных движений рук вверхвниз, вроде тех, что совершает барабанщик, отбивая дробь. Структура моторной программы, построенная по правилам этой модели, показана на рис. 1. Верхний узел (ПЛ) соответствует паре смежных ударов правой и левой рукой т.е. всей программе, за счет периодического повторения которой и возникает непрерывная последовательность движений ПЛПЛПЛ. Два нижележащих узла соответствуют элементарным подпрограммам движениям правой (П) и левой (Л) руки. Предполагается, что некий «импульс «, начиная свой путь от вершины, запускает подпрограмму П (этап 1), затем возвращается (этап 2) в верхний узел, который «знает «, что импульс должен теперь быть направлен для запуска подпрограммы Л (этап 3). Наконец, подпрограмма Л сообщает, что она успешно запущена, и импульс возвращается (этап 4) обратно в вершинный узел. Далее весь описанный процесс происходит снова и снова. При этом на сам процесс «передачи управления » от узла к узлу затрачивается определенное время, которое и определяет наблюдаемые интервалы времени между последовательными движениями правой и левой рук. Хотя эта модель успешно объясняет ряд особенностей временной организации сложных ритмов и сложной двигательной реакции [16], в логическом отношении сведение процесса порождения движения к структуре моторной программы порождает ряд характерных для когнитивизма проблем. Действительно, для того чтобы схема работала правильно, узлы древовидной структуры П и Л (рис. 1) должны обладать внутренним процедурным знанием, присутствующим в описании алгоритма работы программы в виде последовательности шагов вдоль дерева, но никак не представленным в структуре самой древовидной схемы. Так, верхний узел должен какимто образом «знать «, что надо «передавать управление » узлу Л, если до этого работал узел П и, наоборот, запускать движение П, если предыдущим было движение Л.
В отношении другого класса движений движений к цели в рамках когнитивизма рассматривается главным образом баллистическая гипотеза, которая исходит из представления о способности двигательной системы к преобразованию информации о текущем и требуемом положении конечности в информацию о той начальной скорости V (импульсе), которую требуется придать этой конечности, чтобы осуществить заданное перемещение S (рис. 2 а). Это представление лежит в основе нескольких хорошо известных количественных моделей ([5], [13], [16]), которые представляют собой алгоритмы перемещения к цели в виде последовательности шагов (выполнения программы элементарного перемещения). Как именно происходит оценка результатов очередного движения и как определяется начальная скорость движения для оставшегося участка пути, эти вопросы составляют содержание предполагаемого моделью процедурного знания о наличном и требуемом положении конечности и умения на основе этой информации определять начальную скорость ее движения.
Вывод, к которому можно прийти на основе анализа практики когнитивистского моделирования движений, заключается в том, что это направление, основанное на понятии структуры и успешно имитирующее свойства широкого класса движений, не в состоянии тем не менее объяснить сам факт возникновения движений, поскольку возникновение движения есть возникновении структуры, которой до этого не было. Для объяснения здесь требуется привлечь процедурное знание в явном виде.
Рис. 2. Различные модели движения к цели: баллистическая модель (а),
модели точечных аттракторов (б и в)
ТЕОРИЯ САМООРГАНИЗАЦИИ ДВИЖЕНИЙ
Синергетика предлагает радикальное решение проблемы возникновения движений процесс самоорганизации. Сторонники теории самоорганизации движений справедливо указывают на тот факт, что возникновение упорядоченных во времени и в пространстве состояний сложной системы вовсе не требует никакого внутреннего «упорядочивающего механизма » [4], [9], [12]. Ссылаясь на аналогию между сложными системами разной природы (физическими, химическими и биологическими), представители синергетического направления утверждают, что движения также можно рассматривать как спонтанно возникающие макроскопически упорядоченные в пространстве и во времени паттерны коллективного поведения системы динамические структуры. На этом основании предлагается вообще отказаться от понятия репрезентации как понятия излишнего, метафизического и, в частности, отказаться от понятия моторной программы [12].
Источник возникновения таких макроскопически упорядоченных двигательных паттернов синергетика видит не в «инструкциях «, содержащихся в моторной программе, а в спонтанных флуктуациях, неизбежно присутствующих в системе. Математически спонтанные флуктуации можно представить не только как случайную функцию времени, но и в частотной области как континуум бесконечно близких частотных составляющих. Это представление не является формальным: за счет нелинейного взаимодействия между компонентами системы одна или несколько таких частотных составляющих могут «вырасти » до макроскопических размеров, «отобрав » энергию у остальных и тем самым подавив их. Именно так, по мнению синергетиков, возникают упорядоченные структуры (паттерны), описываемые одной или немногими величинами (коллективными переменными). В частности, так возникают ритмические движения (представимые, как известно, в виде суммы синусоидальных составляющих) и именно потому они играют фундаментальную роль в двигательном поведении человека и животных [12], [18].
Важно подчеркнуть, что, говоря о спонтанных флуктуациях, синергетика имеет в виду именно физический сигнал, принимающий самую разнообразную форму: рецепторных потенциалов, потенциалов действия в нейронах, химических процессов и т.п. Следовательно, в отличие от когнитивизма, моделирующего процессы преобразования информации, теория самоорганизации, изучает динамику физического сигнала в сложных нелинейных, открытых и неравновесных системах. То, что самоорганизуется в такой системе, это не информация, а физический сигнал; в этом смысле теория самоорганизации движений является физической теорией.
Что же делает теорию самоорганизации движений более чем просто еще одной
точкой зрения на те же самые явления? Дело в том, что в начале 80-х гг. было обнаружено и изучено экспериментально новое явление явление спонтанного, идущего вопреки намерению перехода от одного способа координации бимануальных ритмических движений к другому.
Вот как выглядит типичный эксперимент [12], в котором наблюдается явление спонтанной смены способа координации бимануальных ритмических движений. Испытуемого просят выполнять реципрокные (разнонаправленные) циклические движения руками в такт с ударами метронома, задающего темп движений. Сначала темп движений невысок (около 1 Гц). Через некоторое время экспериментатор незначительно увеличивает темп метронома (на 0,1 0,2 Гц), и испытуемый, в соответствии с данной ему инструкцией, легко подстраивает темп своих движений под темп метронома. По окончании очередных 20 ударов метронома экспериментатор вновь несколько увеличивает темп метронома, и т.д. Когда частота метронома достигает некоторой критической величины, испытуемые непроизвольно переходят от исходного реципрокного (асинхронного) способа координации к синхронному (синфазному) способу.
В окрестности критической частоты метронома наблюдаются два очень характерных явления: возрастающая нестабильность координации рук (явление, называемое критическими флуктуациями) и увеличение времени, требуемого на возврат к правильному способу координации (критическое замедление). Попросту говоря, немного не доходя до критического темпа испытуемый начинает неожиданно для себя делать много координационных ошибок и тратить больше времени на их исправление. Эти ошибки связаны, однако, не с тем, что испытуемый достиг своего скоростного предела: после того как навязываемый метрономом темп превышает критический, испытуемый легко продолжает отслеживать и этот темп, хотя и переходит при этом к иному, теперь уже синхронному способу координации своих движений.
Более того, в точности такое же явление спонтанной смены реципрокного способа координации синхронными движениями удалось наблюдать и при интерперсональной координации движений, когда двух сидящих человек просили качать ногой в противотакт друг другу в темпе, задаваемом метрономом (см: [12]).
Суть синергетического подхода к объяснению этих явлений заключается в следующем. Прежде всего, предлагается рассматривать разность фаз движения рук в качестве так называемой коллективной переменной, адекватно описывающей процесс координации движений рук. Частота ударов метронома рассматривается как параметр, задающий только темп движения, но не содержащий никаких предписаний относительно способа координации движений, и в этом смысле как неспецифический параметр. Заключенное в инструкции требование к испытуемому начать именно с реципрокных движений, напротив, содержит в себе специфический (об этом ниже) параметр. Качественное изменение в характере координации, т.е. самопроизвольный переход от реципрокных движений к синхронным, предлагается рассматривать как бифуркацию термин, которым обозначают характерное для нелинейных систем явление внезапной смены характера ее динамики. Бифуркация происходит в условиях, когда система становится неустойчивой, и малейших всегда присутствующих в системе флуктуаций достаточно, чтобы (совершенно случайно) система перешла к одному из возможных устойчивых состояний. Предполагается, что по мере изменения темпа метронома система проходит такое неустойчивое состояние, и критическая частота соответствует границе между областью устойчивости реципрокных координаций (ниже критической частоты) и областью устойчивости только синхронных координаций (выше критической частоты). Математическая теория динамики координации бимануальных ритмических движений [11] носит название теории Хакена Келсо Бунца.
Следует, однако, заметить, что синергетический подход к координации движений остается на феноменологической стадии развития он описывает, но не объясняет явления. Убедиться в этом можно, обратившись к узловым логическим моментам теории Хакена Келсо Бунца.
Действительно, на основании опытных данных предполагается, что при выполнении бимануальных ритмических движений руки движутся по синусоидальному закону. Поэтому делается вывод, что разность Dj фаз синусоидальных движений рук адекватно описывает ситуацию их координации (является адекватной коллективной переменной). Далее авторы теории предполагают, что к бимануальным циклическим движениям применимы основные идеи синергетики и поэтому к ним применимо и общее уравнение динамики паттернов dDj/dt=dV(Dj)/dDj.
Здесь V(Dj) сть так называемая потенциальная функция, минимумам которой соответствуют устойчивые значения фазового сдвига, а максимумам неустойчивые. Поскольку потенциальная функция имеет период 2p(V(Dj+2p)=V(Dj)) и является четной, ее можно разложить в ряд Фурье. Это и делают авторы, ограничиваясь первыми членами разложения V(Dj)= a cos(Dj)b cos(2Dj), которые и обладает требуемыми свойствами (рис. 3): устойчивыми оказываются два режима координации синфазные движения (Dj=0) и движения в противофазе (Dj=p) как раз те, что наблюдаются в эксперименте.
Спонтанный переход от одного способа координации к другому авторы модели связывают с закономерным изменением коэффициентов a и b, которое происходит по мере увеличения темпа метронома. Оказывается, что при некотором значении темпа метронома исчезает минимум функции V(Dj), соответствующий реципрокному способу координации, и происходит переход к синхронному способу координации движений, которому соответствует единственный оставшийся минимум (рис. 3).
Далее доказывается, что аналогичное выражение для V(Dj) можно вывести, если исходить из системы дифференциальных уравнений, описывающей динамику двух взаимодействующих нелинейных осцилляторов, т.е. опятьтаки если исходить из осцилляторного, ритмического характера движений. При этом конкретный характер нелинейного дифференциального уравнения подбирается исходя из эмпирических закономерностей ритмических движений уменьшения размаха по мере увеличения их частоты.
Рис. 3. Профиль потенциальной функции V(Dj), определяющей характер координации бимануальных движений в теории Хакена — Келсо — Бунца. По оси абсцисс отложена величина фазового сдвига (Dj), по оси ординат — значение потенциальной функции. Закрашенный кружок соответствует положению системы при реципрокной координации (Dj=p), незакрашенный — системе в состоянии синхронной координации (Dj=0)
Таким образом, феноменологический, имитационный характер теории Хакена Келсо Бунца выражается в том, что объясняемые этой теорией эмпирические факты близкий к синусоидальному характер движений, наличие двух устойчивых режимов координации и спонтанный переход между ними, входят в число необходимых предпосылок самой теории.
В отличие от циклических координаций, для движений к цели не разработана подробная математическая теория, подобная теории Хакена Келсо Бунца. Тем не менее на качественном уровне предлагается рассматривать движение к цели как стремление системы к точечному аттрактору [18]. С позиций синергетики свойство порождать точечные аттракторы, своего рода устойчивые «центры притяжения «, является фундаментальным свойством двигательной системы человека. Характер рассуждений здесь таков. Намерение совершить некоторое действие, например нажать кнопку электрического звонка, приводит к тому, что вместо исходного устойчивого состояния (если до такого намерения рука находилась в покое или
двигалась к какойто иной цели), возникает такое состояние, когда требуемое положение руки (кнопка звонка) является точечным аттрактором. После этого наблюдаемое движение руки определяется динамикой перехода системы к этому новому аттрактору устойчивому положению; рука как бы сама собой «притягивается » к нужному положению. Отпадает всякая проблема выбора направления движения, задания его начальной скорости. Рука ведет себя подобно грузу на растянутой пружине (рис. 2 б) или подобно массивному шарику, всегда скатывающемуся на дно ложбины (рис 2 в).
Как связаны основные понятия теории самоорганизации движений с объяснительным инструментарием традиционных психологических теорий управления движениями? Поясняя основной тезис синергетики, М. Турвей [18] подчеркивает: «Простота может быть следствием простых (низкоразмерных) динамических законов и высокоупорядоченных информационных структур » [18; 952]. Последнее добавление чрезвычайно характерно, поскольку «высокоупорядоченные информационные структуры » есть, конечно, не что иное как структурированное декларативное знание, т.е. основной предмет когнитивной психологии. В теории самоорганизации движений такие высокоупорядоченные информационные структуры играют роль начальных и граничных условий для динамики коллективной переменной (C. Келсо называет их «информационноспецифическими граничными условиями «). Фактически, информационные граничные условия принципиально ничем не отличается от программы движения. Различие между синергетикой и когнитивизмом заключается в том, что последний пытается явно сконструировать информационную модель движения, в то время как синергетика, признавая принципиальную необходимость информационных процессов, ничего не говорит о их возможной структуре.
Более того, концепция внутренней репрезентации неявно присутствует в рассуждениях синергетиков. Например, нетрудно заметить, что зависящая от параметров a и b потенциальная функция V(Dj) (рис. 3) является внутренней репрезентацией динамики координации бимануальных ритмических движений, хотя она и не имеет привычной для когнитивистского моделирования формы блоксхемы. Потенциальный профиль V(Dj) выполняет по сути дела ту же роль, что и обобщенная программа [17], зависящая от параметров a и b. Необходимость в декларативном знании, в концепции репрезентации отчетливо просматривается и в синергетическом подходе к интенции и двигательному научению [12]. Так, интенция «рассматривается как специфическая информация, влияющая на динамику паттернов таким образом, чтобы система перешла в желаемое состояние. Это означает, что интенция является неким неотъемлемым, имманентным аспектом динамики паттернов, стабилизирующим или дестабилизирующим то состояние, которое уже есть в настоящий момент » [12; 141]. В терминах математической теории Хакена Келсо Бунца интенция это влияние на динамику координационных паттернов, сводящееся к такому изменению профиля потенциальной функции V(Dj), которое бы обеспечило переход системы к требуемому режиму координации бимануальных движений. Совершенно очевидно, что динамика интенции в полной мере опирается на понятие потенциального профиля, т.е. на понятие внутренней репрезентации.
Таким образом, стремление изгнать концепцию «репрезентации » привело лишь к ее возвращению в иной форме. Понятия «информации » и «репрезентации » остались логически необходимыми атрибутами теории, приобретя форму «потенциальных профилей » и «информационноспецифических » начальных и граничных условий. Более того, само понятие информационноспецифических граничных условий в рамках синергетического подхода остается пока чисто декларативным понятием: не существует никаких способов предсказать, какие именно граничные условия должны быть заданы для того, чтобы возникло движение требуемого характера.
Логические трудности теории самоорганизации движений связаны с тем, что
она, отвергая понятие репрезентации движения в виде моторной программы, пытается вообще обойтись без явного рассмотрения структурных особенностей исследуемых систем. Если конкретная структура двигательной системы человека от биомеханики до ЦНС не важна в отношении самой способности формирования упорядоченных паттернов двигательного поведения (с чем еще можно согласиться), то репертуар таких «паттернов » и сложность их динамики должны зависеть от структурных особенностей телесной, мозговой и психической организации. В противном случае совершенно непонятно, почему в филогенезе наблюдается отчетливое и закономерное усложнение двигательной системы и специализация ее отделов и почему характер совершаемых движений да и сама возможность совершать произвольные движения так специфически зависит от нарушений структуры мозга и от прижизненного опыта.
Математическое моделирование движений в рамках синергетики свелось к формализации при помощи аппарата дифференциальных уравнений лишь предполагаемого в наличии когнитивистами «процедурного знания «. Напротив, активно рассматриваемое когнитивистами «декларативное знание » приняло форму «информационноспецифических » начальных и граничных условий.
МАТЕМАТИКА ОПЕРАТОРОВ И ОПИСАНИЕ ДВИЖЕНИЙ
Нетрудно заметить, что рассмотренные два подхода когнитивизм и синергетика взаимно дополняют друг друга. Когнитивизм изучает как моторные программы то, что синергетика обозначает как информационноспецифические граничные условия, а синергетика пытается ответить на вопрос, как именно возникают те упорядоченные внутренние структуры, наличие которых просто предполагается когнитивизмом в качестве предсуществующего процедурного знания.
Принципиальные черты и когнитивистского подхода, и теории самоорганизации движений, оформившихся позднее в виде самостоятельных теоретических направлений, присутствуют в представлении Н.А. Бернштейна о сенсорных синтезах, характер и возможности которых положены им в основу уровней построения движений [1]. Можно предположить, что простейшие синтезы, характерные для уровня палеорегуляции движений (A) и уровня синергий (B), это как раз те уровни построения движений, которые адекватно описываются с точки зрения синергетики. Напротив, высшие синтезы, которые мы находим на уровне действия (D), характеризуются прежде всего инвариантностью цели при значительной вариативности двигательного решения задачи. Такие синтезы немыслимы без «модели потребного будущего «, которая носит ярко выраженный «информационный » характер.
Как мы уже отмечали, когнитивизм и синергетика рассматривают главным образом двигательные стереотипы. В этом отношении оба направления далеки от того, чтобы описать количественно то специфическое, что привносит в построение движений собственно уровень действия. И «схемотехника » когнитивистского подхода, имитирующая наблюдаемое двигательное поведение, и используемый синергетикой аппарат дифференциальных уравнений, описывающих эволюцию коллективной переменной, приспособлены скорее для описания технических фонов. Собственно уровень действия не анализируется; он лишь предполагается в наличии, скрываясь за терминами «план движения «, «двигательное намерение » или «информационноспецифические граничные условия «.
Повидимому, математическое моделирование уровня действия слишком грандиозная задача. Едва ли она может быть решена в настоящее время, поскольку объектом моделирования в этом случае является не динамика движений, а динамика целей движений. Более реальной задачей могло бы стать выявление в наблюдаемом пространственновременном рисунке движения фоновых (предсказуемых, почти детерминированных) его составляющих и, наоборот, экстемпоральных, не предсказуемых на основе предыдущих
участков движения событий. Смысл этих событий состоит в переключении фоновых движений. Именно события, а не состояния характеризуют уровень действия. В отличие от простейших фоновых автоматизмов, построению действия свойственна определенная асинхрония, отсутствие механической регулярности. Поэтому скорее перерывы в регулярности движения или изменения характера этой регулярности, а не сама регулярность (периодические изменения в скорости движения) характеризуют структуру действия. Так, взяв в качестве примера движения скрипача, выполняющего вибрато [1], можно утверждать, что именно эти два события переход к состоянию вибрато от предыдущего исполнительского приема и последующий переход от вибрато к движению другого характера составляют структурную особенность действия. Само же циклическое движение, реализующее вибрато, является целостным, неделимым. В этом смысле весь отрезок или «вспышку » такого циклического движения, воспользовавшись терминологией В.П. Зинченко и Н.Д. Гордеевой ([5], [7]), вполне можно назвать «квантом действия » или, подругому, «движениемсостоянием «, не разложимым более на «элементарные части «. Выделение фоновых составляющих движения и моментов их переключения могло бы оказаться полезным как для изучения действия в целом (которое в этом случае могло бы характеризоваться характером событий и их частотой), так и для изучения собственно технических фоновых движений.
Из предыдущих рассуждений следует, что любая математическая модель действия должна какимто образом описывать как фоновую, предсказуемую его часть, так и те события, которые асинхронно «вторгаются » в плавный ход выполнения движения. Для описания движений можно использовать математику операторов математику абстрактных преобразований сигнала. Такая идея высказывалась еще в 1948 г. Н. Винером, создателем кибернетики [3], и подробно обсуждалась Н.А. Бернштейном [2].
К сожалению, эта идея не получила должного развития. Казалось совершенно естественным, что для использования математики операторов необходимо совершенно точно знать структуру (математический вид) оператора и что это совершенно нереально, учитывая фантастическую сложность двигательной системы. Такая точка зрения безусловно верна, если речь идет о совершенно точном количественном предсказании пространственновременной формы движения. Однако, как нам представляется, это не мешает сделать существенные выводы относительно общих свойств движения (таких, как периодичность), которыми движение будет обладать и в том случае, если даже точная математическая форма оператора не задана, но известен класс операторов.
Проиллюстрируем возможности математики операторов на примере ритмических движений, уже рассмотренных нами выше с позиций когнитивистского моделирования и теории самоорганизации движений.
Напомним, что в соответствии с теоретической концепцией Н.А. Бернштейна для решения конкретной двигательной задачи создается уникальная функциональная система (функциональный орган), характеризуемая кольцевым строением. Такая система объединяет в единое целое внутренние и внешние условия выполнения действия и остается замкнутой в том смысле, что она «стремится » компенсировать всевозможные внешние и внутренние влияния, мешающие выполнению двигательной задачи.
В математическом отношении подобная замкнутая система может быть описана абстрактным операторным уравнением, связывающим посредством некоторого оператора Op наблюдаемую величину (например, положение руки в пространстве) с предыдущими значениями этой величины. В физическом (энергетическом) отношении движение управляется сигналом, возникающим из присутствующих в системе спонтанных флуктуаций e(t). Характер движения (его информационное содержание) определяется видом оператора Op, т.е. конкретными свойствами построенной для решения данной задачи функциональной системы. Функционирование такой замкнутой системы
описывается абстрактным операторным уравнением: x(t)=Op+e(t).
При этом функциональная роль уровня действия D, повидимому, и заключается в целесообразной смене структуры замкнутой функциональной системы, чему на языке математики соответствует смена формы оператора Op, описывающего преобразования сигнала в этой системе. Отметим, что с позиций синергетики смене вида оператора соответствует изменение «информационноспецифических » граничных условий, а с позиций когнитивизма смена моторных программ. Однако до тех пор, пока оператор остается неизменным, движение носит почти предсказуемый характер (с точностью до «шума » e(t)), и пространственновременной рисунок зависит только от структуры оператора Op.
Любопытным примером замкнутой системы является «рефлекторное кольцо «, в котором вообще не происходит никаких преобразований сигнала, кроме задержки на время d и некоторого ослабления (с коэффициентом k, |k|
Как это ни покажется удивительным, но именно такая система наилучшим образом приспособлена к порождению каких угодно ритмических движений. Действительно, при k=1 и e(t)=0 получим, что x(t)=x(td), что, в свою очередь, является просто математическим определением любой периодической функции с периодом d. Если же коэффициент k меньше единицы, но достаточно близок к ней, а e(t)¹0, то в этой системе возникнут квазипериодические принципиально вариативные движения. Следовательно, функциональная система, организованная в виде кольца, способна порождать ритмические движения, рекрутируя (фильтруя) необходимый сигнал из спонтанных флуктуаций e(t). Для этого не требуется никакого управляющего кольцом центрального таймера напротив, функциональная система сама выступает в роли таймера. В то же время изменение вида оператора, т.е. перестройка функциональной системы, требует управления. В рассмотренном примере простейшей замкнутой системы для изменения амплитуды движения потребовалось бы изменить коэффициент усиления k, а для изменения частоты (периода) ритмических движений задержку d. Подробный количественный анализ свойств этой модели, а также численный эксперимент показывают, что эта модель в состоянии объяснить процесс порождения и характер координации простейших ритмических движений [8].
Сопоставление обсуждавшихся выше теоретических точек зрения на природу движения указывает на наличие двух типов присущей движению вариативности «технической «, связанной с процессом порождения движения из спонтанных флуктуаций, и вариативности, связанной с перестройкой функциональной системы в процессе совершения движения. Повидимому, ряд общих свойств движений, в особенности фоновых, таких как ритмичность, может быть связан не со специальными «предусмотренными » на этот случай механизмами, а просто с «топологическими » свойствами замкнутых и организованных по принципу кольца функциональных систем со стационарностью, замкнутостью и конечным временем распространения сигнала вдоль кольца. В этом отношении усилия, направленные на математическое описание замкнутых функциональных систем и возникающих в них фоновых «собственных » движений, представляются вполне оправданными. В то же время при описании самого процесса последовательной организации подвижных функциональных систем преимущество, повидимому, остается на стороне качественных методов анализа движения и, возможно, дискретного когнитивистского моделирования.
1. Бернштейн Н.А. О построении движений. М.: Медгиз, 1947.
2. Бернштейн Н.А. Очерки по физиологии движений и физиологии активности. М.: Медицина, 1966.
3. Винер Н. Кибернетика. М.: Наука, 1983
4. Волькенштейн М.В. Биофизика. М.: Наука, 1988.
5. Гордеева Н.Д. Экспериментальная психология исполнительного действия. М.: Тривола, 1995.
6. Гордеева Н.Д., Евсевичева И.В., Зинченко В.П. К проблеме реактивности и чувствительности
предметного действия // Интеллектуальные процессы и их моделирование. Пространственновременная организация. М.: Наука, 1991.
7. Гордеева Н.Д., Зинченко В.П. О роли когнитивных компонентов в функциональной структуре предметного действия // Психология восприятия. Материалы советсконорвежского симпозиума. М.: Наука, 1989. С. 84100.
8. Курганский А.В. О возникновении и координации ритмических движений // Теория и практика физической культуры. 1996. № 11. С. 4449.
9. Пригожин И. От существующего к возникающему. М.: Наука, 1985.
🎬 Видео
Урок 7. Механическое движение. Основные определения кинематики.Скачать

Математическая модель задачи. Как составить. Математическая постановка. Исследование операций.Скачать

ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ. Видеоурок | АЛГЕБРА 7 классСкачать

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ//#МАТЕМАТИКА_ПРОСТОСкачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать