S: Гиперболической модельюне является регрессионная модель …
-:
-:
-:
+:
S: Для линеаризации нелинейной регрессионной модели 
-:
-:
+:
-:
S: При расчете уравнения нелинейной регрессии 
S: Для регрессионной модели математическое ожидание остатков равно 0, следовательно, оценки параметров обладают свойством …
S: Для оценки параметров эконометрической модели линейного уравнения регрессии вида 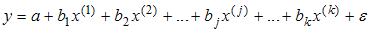
+:
-:
-:
-:
S: Для регрессионной модели зависимости потребления материала на единицу продукции от объема выпуска продукции построено нелинейное уравнение (см. рис.).

Значение индекса детерминации для данного уравнения составляет R 2 =0,904.
Следовательно,
-: объемом выпуска продукции объяснено 9,6% дисперсии потребления материалов на единицу продукции
+: объемом выпуска продукции объяснено 90,4% дисперсии потребления материалов на единицу продукции
-: потреблением материалов на единицу продукции объяснено 9,6% дисперсии объема выпуска продукции
-: потреблением материалов на единицу продукции объяснено 90,4% дисперсии объема выпуска продукции
S: Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе
-: параболы второй степени
S:
S:
-: квартира с балконом стоит на 1,05 долл. дороже аналогичной квартиры без балкона
-: один квадратный метр жилья стоит 450 долл.
-: один квадратный метр квартиры с балконом стоит 450 долл.
+: наличие балкона не влияет на цену квартиры
S:
-:
+:
-:
-:
S:
S:
+: среднее значение зависимой переменной при нулевых значениях независимых (объясняющих) переменных
-: влияние случайных факторов на зависимую переменную модели у
-: среднее изменение зависимой переменной модели у при изменении независимых переменных на единицу
-: среднее значение независимой переменной при нулевых значениях зависимых переменных
S: Переменные, принимающие значения 0 и 1, которые вводят в модель множественной регрессии для количественного задания некоторого качественного признака, называются __________ переменньми.
S: Выбор вида эконометрической модели на основании соответствующей теории связи между переменными называется ______ модели.
S:
-:
-:
-:
S: Оценки являются _____________, если при увеличении количества
наблюдений, точность оценок тоже увеличивается.
S: Для оценки параметров линейной регрессионной модели с
_________ остатками применяется обобщенный метод
S:
-: неопределенной ситуации относительно автокорреляции остатков
-: отрицательной автокорреляции в остатках
+: отсутствия автокорреляции в остатках
-: положительной автокорреляции в остатках
S:
S:
+: минимума суммы квадратов отклонений
-: равенства нулю суммы модулей отклонений
-: минимума суммы модулей отклонений
-: равенства нулю суммы квадратов отклонений
S: Оценки параметров, найденных при ______ метода
наименьших квадратов, обладают свойствами несмещенности, эффективности и состоятельности.
S: В случае регрессионной модели с автокоррелированными и / или
гетероскедастичными остатками рассматривают _________ модель
S: Известно, что теснота связи между х и у средняя, при увеличении независимой переменной х значение зависимой переменной у увеличивается. Тогда значение коэффициента корреляции для такой модели парной линейной регрессии находится в интервале .
S: Долю объясненной с помощью регрессии дисперсии в общей дисперсии зависимой переменной характеризует .
S:
-: других параметров не подтвердилась
-: этого параметра не подтвердилась
+: этого параметра подтвердилась
-: других параметров подтвердилась
S:
-: суммой квадратов отклонении, не объясненных регрессией
-: общей суммой квадратов отклонений
+: суммой квадратов отклонений, объясненных регрессией
-: остаточной суммой квадратов отклонений
S:
-: суммой квадратов отклонений, объясненных регрессией
-: остаточной суммой квадратов отклонений
-: суммой квадратов отклонений, необъясненных регрессией
+: общей суммой квадратов отклонений
S: Параметры регрессии, выраженной внутренне линейной функцией, нелинейной относительно параметров, после линеаризации можно оценить при помощи _________ метода наименьших квадратов.
S: Самым простым методом линеаризации нелинейной функции, гашенной относительно параметров, является .
-: применение элементарных преобразования с использованием замены переменных
-: разложение функции в ряд Тейлора
S:
+: разложение в ряд Тейлора
S: Априорно известно, что зависимость между объясняющей и объясняемой переменными не является линейной, в таком случае зависимость может быть выражена ________ функцией.
S: Методом линеаризации внутренне линейной функции, нелинейной относительно параметров, является .
+: применение элементарных преобразования с использованием замены переменных
-: разложение функции в ряд Тейлора
S: Убывающая или возрастающая компонента временного ряда, характеризующая совокупное долговременное воздействие множества факторов, называется ___________ компонентой.
S: Коэффициент автокорреляции характеризует тесноту ________ связи.
S: Сумма скорректированных сезонных компонент для мультипликационной модели равна .
S:
-: неизменностью функции регрессии во времени
-: гомоскедастичностью его остатков
+: наличием в его структуре тренда
-: постоянством дисперсии его уровней
S: Сумма скорректированных сезонных компонент для аддитивной модели равна .
S: Автокорреляционная функция является отображением зависимости между значениями соответствующего коэффициента автокорреляции
-: периодами (моментами) времени
S:
-: моделью, включающей фактор времени
-: моделью с распределенным лагом
S: Предпосылками метода наименьших квадратов (МНК) являются следующие …
-: отсутствие автокорреляции в остатках
-: присутствие в эконометрической модели более чем двух факторов
-: функциональная связь между зависимой и независимой переменными
S: Несмещенность оценки характеризуется …
-: зависимостью от объема выборки значения математического ожидания остатков
+: равенством нулю математического ожидания остатков
-: максимальной дисперсией остатков
-: отсутствием накопления остатков при большом числе выборочных оцениваний
S: Метод наименьших квадратов применим к уравнениям регрессии, …
-: которые отражают нелинейную зависимость между двумя экономическими показателями и не могут быть приведены к линейному виду
-: которые отражают нелинейную зависимость между двумя экономическими показателями, но могут быть приведены к линейному виду
+: которые отражают линейную зависимость между двумя экономическими показателями
S: Обобщенный метод наименьших квадратов подразумевает …
-: переход от множественной регрессии к парной
+: введение в выражение для дисперсии остатков коэффициента пропорциональности
-: двухэтапное применение метода наименьших квадратов
S: К видам эконометрических моделей по типам зависимости относятся модели …
+: систем эконометрических уравнений
S: Отбор факторов в эконометрическую модель множественной регрессии может быть осуществлен на основе …
+: матрицы парных коэффициентов корреляции
-: сравнения коэффициентов «чистой» регрессии
-: значений коэффициентов автокорреляции уровней ряда различных порядков
-: сравнения остаточной дисперсии до и после включения фактора в модель
S: В линейном уравнении парной регрессии 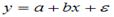
S: Фиктивная переменная может принимать значения:
-: в интервале от –1 до 1
S: Пусть t – рассчитанная для коэффициента регрессии статистика Стьюдента, а tкрит – критическое значение этой статистики. Коэффициент регрессии считается статистически значимым, если выполняются следующие неравенства:
-:
+:
-:
-:
S: Для зависимости спроса на некоторый товар от цены за единицу товара и дохода потребителя получено уравнение регрессии вида 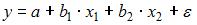
-:
+:
-:
S: Основные характеристики строго стационарного временного ряда 
+: не зависят от t
-: меняются при изменении начала отсчета времени t
-: зависят от величины 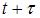

S: Построение модели временного ряда может быть осуществлено с использованием …
+: метода последовательных разностей
S: Система эконометрических уравнений включает в себя следующие переменные:
S: Эндогенные переменные …
-: не зависят от экзогенных переменных
+: могут быть объектом регулирования
-: влияют на экзогенные переменные
-: могут коррелировать с ошибками регрессии
S: Дано уравнение регрессии 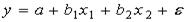
-: полиномиальное уравнение множественной регрессии
+: линейное уравнение множественной регрессии
-: полиномиальное уравнение парной регрессии
-: линейное уравнение простой регрессии
S: Математическая форма записи уравнения зависимости переменной у от одного или нескольких факторов х называется ______ эконометрической модели.
S: Отбрасывание значимой переменной в уравнении множественной регрессии является ошибкой .
S: Отправной точкой эконометрического исследования является…
+: определение спецификации модели
-: проверка качества модели
-: оценка погрешности модели
S: При выборе спецификации модели парная регрессия используется в случае, если среди множества факторов, влияющих на результат …
+: можно выделить доминирующий фактор
-: нельзя выделить доминирующий фактор
-: можно выделить несколько факторов
-: можно выделить лишь случайные факторы
S: Примером модели множественной регрессии является:
S: Относительно количества факторов, включенных в уравнение регрессии, различают регрессии …
+: простую и множественную
-: парную и линейную
-: нелинейную и множественную
-: множественную и многофакторную
S: При отборе факторов множественного линейного уравнения регрессии число факторов в .
+: 6-7 раз меньше объема выборки по которой строится регрессия
-: 6-7 раз больше объема выборки по которой строится регрессия
-: 6-7 раз больше количества параметров уравнения
-: 6-7 раз меньше количества параметров уравнения
S: Значения матрицы парных коэффициентов корреляции не характеризуют …
-: значение коэффициента множественной корреляции
-: тесноту линейной связи между двумя переменными
+: статистическую значимость построенного уравнения
-: наличие коллинеарных факторов в модели
S: Из пары коллинеарных факторов в эконометрическую модель включается тот фактор, который при _______ связи с результатом имеет меньшую связь с другими факторами.
Видео:Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Дифференцированного
Читайте также:
|
Тест 1.
Если в модели опущена переменная, которая должна быть включена, то оценки коэффициентов регрессии могут оказаться смещенными
Проблемой спецификации не является расчет оценок параметров эконометрической модели
| Один из этапов построения эконометрической модели, на котором проверяются статистические свойства построенной модели, называется … верификацией. Качество регрессионной модели ухудшается в случае _____ количества оцениваемых параметров при _____ объёме выборки большого,небольшой |
| верификацией модели |
Объем выборки для построения эконометрической модели ограничен сверху объемом генеральной совокупности
| Эконометрика синтезирует в себе науки: |
| экономическую теорию, математическую статистику и экономическую статистику Эконометрическая модель — это математическая Модель |
Реальной экономической системы (объекта), построенная на статистических данных
Спецификацией эконометрической модели является математическая форма записи уравнения зависимости переменной у от одного или нескольких факторов х
Формализация закономерностей общей экономической теории является одним из принципов ______ эконометрической модели спецификации
| Вопрос | Пусть истинной моделью является  (х1, х2, х3 — существенные факторы), однако, мы не имеем статистических данных по переменной (х1, х2, х3 — существенные факторы), однако, мы не имеем статистических данных по переменной  . Но другая переменная . Но другая переменная  выступает идеальным заменителем для нее в том смысле, что имеется строгая (функциональная) линейная связь выступает идеальным заменителем для нее в том смысле, что имеется строгая (функциональная) линейная связь  , где , где  и и  являются постоянными, но неизвестными величинами. Если мы построим регрессию являются постоянными, но неизвестными величинами. Если мы построим регрессию  , то , то |
оценки b2 и b3 будут такими же, как и при построении регрессии с использованием  |
Тест 4.
К причинам присутствия в эконометрической модели случайного фактора относятся:
-невозможность включения в модель всех объясняющих переменных
-стохастический характер зависимости
В линейном уравнении парной регрессии  переменными являются x,y В эконометрическую модель множественной регрессии необходимо включить факторы, оказывающие ________ влияние на исследуемый показатель существенное Верным является утверждение, что параметр Регрессии является детерминированной величиной, а его оценка – случайной В частном уравнении регрессии факторных переменных ___________ по сравнению с исходным уравнением множественной регрессии, по которому оно построено всегда меньше переменными являются x,y В эконометрическую модель множественной регрессии необходимо включить факторы, оказывающие ________ влияние на исследуемый показатель существенное Верным является утверждение, что параметр Регрессии является детерминированной величиной, а его оценка – случайной В частном уравнении регрессии факторных переменных ___________ по сравнению с исходным уравнением множественной регрессии, по которому оно построено всегда меньше |
В линейном уравнении парной регрессии  переменными не являются a b переменными не являются a b |
В линейном уравнении множественной регрессии  коэффициентами регрессии являются b1 b2 коэффициентами регрессии являются b1 b2 |
Линейное уравнение множественной регрессии имеет вид  . Определите какой из факторов . Определите какой из факторов  или или  оказывает более сильное влияние на у по этому уравнению нельзя ответить на поставленный вопрос, так как коэффициенты регрессии несравнимы между собой В линейной регрессии Y=b0+b1X+e переменными уравнения регрессии являются x y оказывает более сильное влияние на у по этому уравнению нельзя ответить на поставленный вопрос, так как коэффициенты регрессии несравнимы между собой В линейной регрессии Y=b0+b1X+e переменными уравнения регрессии являются x y
Тест 5.
Для определения оценок коэффициентов линейного уравнения регрессии использовать метод наименьших модулей, наименьш квадратов При применении метода наименьших квадратов к оценке параметров уравнений регрессии, величина зависимой переменной y не может определяться на основании _______ уравнения регрессии Нелинейного дифференцированного Метод наименьших квадратов предназначен для оценки параметров линейной эконометрической модели на основании результатов наблюдений, содержащих случайные ошибки При применении метода наименьших квадратов к оценке параметров уравнений регрессии, величина зависимой переменной y может определяться на основании _______ уравнения регрессии Линеаризованного Линейного
в минимизации функции Для линейной регрессионной зависимости система нормальных уравнений линейная относительно параметров регрессии Название метода «метод наименьших квадратов» подразумевает, что сумма квадратов отклонений значений результирующего признака от теоретических должна быть минимальной В рамках метода наименьших квадратов (МНК) система нормальных уравнений – это система, решением которой являются оценки параметров теоретической модели Метод наименьших квадратов применяется для —выбора оптимальной линии из всех возможных -для описания линейной зависимости некоторого поля корреляции -оценки параметров линейных уравнений регрессии Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.038 сек.) Видео:Математика без Ху!ни. Метод Гаусса.Скачать  Для автокорреляции характерным является соотношение COVДля автокорреляции характерным является соотношение COV(ui, uj) НЕ РАВНА 0: Для анализа значимости оценок параметров линейной регрессии применяется: Для каких целей нужна контролирующая выборка? для проверки адекватности оцененной модели (По построенной модели строится прогноз значений объясняющей переменной из контролирующей выборки и доверительные интервалы для истинных значений) Для каких целей нужна обучающая выборка? для проверки адекватности оцененной модели (По обучающей выборке выполняется оценка параметров модели методом наименьших квадратов и строится регрессионная модель) Для каких целей предназначена приведённая форма эконометрической модели? для прогноза (объяснения) эндогенных переменных при помощи экзогенных переменных Для каких целей предназначена статистика Для проверки 3-его условия теоремы Гаусса-Маркова о наличии или отсутствия автокорреляции (Тест Дарбина–Уотсона (DW)). для тестирования предпосылки теоремы Гаусса-Маркова Н0: Var(u1) = Var(u2)= …= Var(un) = уu2 Для каких целей предназначена статистика Для проверки статистической гипотезы о равенстве дисперсий случайных остатков в наблюдаемых уравнениях (Тест Голдфелда-Квандта), для тестирования предпосылки теоремы Гаусса-Маркова Н0: Var(u1) = Var(u2)= …= Var(un) = уu2 Для каких целей предназначено датирование переменных модели? Для построения модели с учетом динамики (фактора времени) 9. Для линейного уравнения регрессии y = a + bx+u метод наименьших квадратов используется при оценивании параметров a и b. 10. Для уравнения зависимости предложения на некоторый товар от цены за единицу товара получено значение коэффициента детерминации, равное 0,64. Следовательно, на 64% вариация предложения товара обусловлена его ценой, а на 36% она обусловлена прочими факторами. + отношение факторной дисперсии предложения к его общей дисперсии равно 64% + отношение остаточной дисперсии предложения к его общей дисперсии равно 36% 11. Для учета действия на зависимую переменную факторов качественного характера (так называемых фиктивных переменных) последним могут присваиваться 0 или 1. 12. Если = ХХХ, то какая линейная связь между x и y: 13. Если автокорреляция отсутствует, то DW ≈ 2 (принадлежит интервалу от du до 4-du) 14. Если все наблюдения лежат на линии регрессии, то коэффициент детерминации R2 для модели парной регрессии равен 1 15. Если все предпосылки теоремы Гаусса-Маркова справедливы и случайные возмущения распределены нормально, то статистика теста Голдфелда-Квандта распределена по закону Фишера. 16. Если две переменные независимы, то их теоретическая ковариация равна 0. 17. Если парный коэффициент корреляции между признаками Y и X принимает значение 0,67, то коэффициент детерминации равен: 0,449 (квадрат из R^2) 18. Если предположение о природе гетероскедастичности верно, то дисперсия случайного члена для первых наблюдений в упорядоченном ряду будет : ——Ниже, чем для последних 19. Если предпосылки МНК не выполняются, то остатки могут Считаться неслучайными, модель неадекватна, быть не равны 0; не подчиняться закону, нормального распределения; быть гетероскедастичными 20. Знания каких из перечисленных ниже параметров требует тест Голдфелда-Квандта? Величины Fкрит, xi, квадраты остатков ESS 21. Значение статистики Дарбина-Уотсона находится между значениями:— 0 и 4 22. Известно, что с увеличением объема производства себестоимость единицы продукции уменьшается за счет того, что происходит перераспределение постоянных издержек. Пусть а — совокупная величина постоянных издержек, а b — величина переменных издержек в расчете на одно изделие. Тогда зависимость себестоимости единицы продукции от объема производства можно описать с помощью модели Возможные ответы: обратная зависимость; линейная модель типа y=a0+a1x1, где a1 0. Она предназначена для объяснения текущего уровня инвестиций It величиной ДYt-1= Yt-1 — Yt-2 цепного прироста ВВП за предыдущий период времени. Заметим, что в модели (4.1) величина ДYt-1 играет роль экзогенной переменной, a It — эндогенной переменной. Спецификация (4.1) содержит два неизвестных параметра: b, уu. Число объясняющих переменных, количество наблюдений в выборке. 75. Относительные отклонения расчётных значений результирующего признака от его наблюдаемых значений используются при расчёте … 76. Отрицательная автокорреляция – ситуация, когда случайный член регрессии в следующем наблюдении ожидается: Знака, противоположного знаку случайного члена в настоящем наблюдении. (корреляция между последовательными значениями случайного члена отрицательна). Множественной линейной. ее математическое ожидание равно истинному значению оцениваемого параметра (нет систематической ошибки) математическое ожидание остатков равно нулю. Оценка 79. Оценку существенности (значимости) отдельного параметра уравнения регрессии можно проводить на основании показателей. множественного коэффициента корреляции 80. Ошибки спецификации возникают в том случае, если: неправильно определен список параметров или неправильно сделан выбор математической модели взаимосвязи между переменными 81. По аналитическому выражению различают связи: +линейные и нелинейные 82. По какой из приведенных ниже формул рассчитываются индивидуальные показатели информационной ёмкости:
83. По уравнению регрессии y= f(х)+e рассчитано значение коэффициента корреляции, которое характеризует тесноту связи между … факторным и результативным признаками 84. Полиномиальной является эконометрическая модель вида. +y=a+bx+cx2+e 85. Предпосылками МНК являются:
+нулевая средняя величина остатков +гомоскедастичность +отсутствие автокорреляции остатков +случайные отклонения являются независимыми друг от друга + дисперсия случайных отклонений постоянна для всех наблюдений 86. При наличии автокорреляции случайной величины оценка коэффициентов регрессии становится: неэффективными (неудовлетворительным) При отрицательной автокорреляции DW: —Больше 2. Проверку выполнения предпосылки МНК (метода наименьших квадратов) о гомоскедстичности (гетероскедастичности) остатков можно провести +визуально по графику +на основании параметрических тестов Процесс выбора необходимых переменных для регрессии переменных и отбрасывание лишних переменных называется: спецификацией переменных Различают четыре принципа спецификации экономических моделей. Какой из принципов (укажите номер) описывает следующий текст: «… чтобы количество уравнений, составляющих спецификацию модели, в точности совпадало с количеством эндогенных переменных, включённых в модель»——второй Разность (1-R2), где R2 — коэффициент детерминации. оценивает влияние неучтенных в модели факторов С каким параметром совпадает физическая размерность переменной u в рамках модели Подтверждается существование автокорреляции и гипотеза отклоняется 103. Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК, является—— линейность параметров 104. Укажите количество эндогенных переменных, имеющихся в модели спроса-предложения товара на конкурентном рынке? три (сколько уравнений, столько и эндогенных переменных) 105. Укажите последовательность этапов проведения теста Голдфелда-Квандта для парной линейной регрессии: Шаг 1. Уравнения наблюдений упорядочивают по возрастанию объясняющей переменной x. Шаг 2. Полученный отсортированный массив разбивают на две равные части (n1 = n2 = n/2). Если массив большой или количество значений в массиве нечетное (для небольших массивов), то его разбивают на 3 части (n1 = n3 ≈ 0,3n). Шаг 3. Для первой части отсортированного массива рассчитывается величина ESS1: Шаг 4. Аналогично рассчитывается величина ESS2 для другой части отсортированного массива: Шаг 5. Вычисляется статистика Голдфелда-Квандта (GQ): Шаг 6. Задается уровень значимости б и при количествах степеней свободы обоих частей массива v1 = v2 = n1-(k+1) определяется Fкрит = F1-б распределения Фишера Шаг 7. Гипотеза Н0 принимается, если справедливы следующие два неравенства GQ ≤ Fкрит, GQ-1 ≤ Fкрит, т. е. случайный остаток в парной эконометрической модели в этом случае полагается гомоскедастичным. В противном случае гипотеза Н0 отклоняется и делается вывод, что случайный остаток в парной эконометрической модели является гетероскедастичным. 1. Упорядочение наблюдений по возрастанию значений объясняющей переменной. 2. Оценка регрессий для k-первых и k-последних наблюдений. 3. Оценка сумм квадратов отклонений для регрессий по k-первым и k-последним наблюдениям. 4. Вычисление статистики Фишера. 106. Укажите последствия мультиколлинеарности:
107. Укажите правильную последовательность этапов исследования эконометрической модели из предложенных ниже: спецификация – сбор информации – параметризация – верификация 1. Постановочный этап 2. Априорный этап 3. Этап параметризации и спецификации 4. Информационный этап 5. Этап идентификации модели 6. Этап верификации модели 108. Укажите требования к переменным, включаемым в модель множественной линейной регрессии:
109. Что вычисляется по формуле: 110. Укажите условия, которые выполняются, если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности: ● наименьшая дисперсия остатков ● равенство нулю математического ожидания остатков из теории ● Все условия Гауса-Маркова: 111. Укажите число поведенческих уравнений в простой макромодели Кейнса, Одно поведенческое уравнение 112. Укажите, если справедлива гипотеза H0: a1 = 0 модели парной регрессии, то спецификация модели является: 113. Укажите, какой является спецификация модели, если справедлива гипотеза H0: a1 =0 относительно коэффициента a1 модели парной регрессии y = a0 + a1∙x+u: 114. Условие гетероскедастичности означает, что вероятность того, что случайный член примет какое-либо конкретное значение ___ наблюдений: одинакова для всех 115. Установите соответствие между наименованиями элементов уравнения уi=a+a1x1i+ . +akx2i+. +anхni +ui и их буквенными обозначениями: ● параметры регрессии – a1…an ● объясняющая переменная (экзогенный) — X ● объясняемая переменная (эндогенный) — Y ● случайные отклонения – e (ui) 116. Факторы, включаемые в модель, должны отвечать следующим требованиям: ● Они должны быть количественно измеримы (количественная соизмеримость) 117. Факторы являются коллинеарными, если коэффициент корреляции между ними по модулю больше 0,7 (т. е. |���������� | ≥ 0,7) 118. Характеристикой чего служит величина ���� (среднеквадратическая ошибка прогнозируемого показателя) Чем больше число наблюдений, тем __________ зона неопределенности для критерия Дарбина-Уотсона: —уже, меньше Чем характеризуется несмещенность оценки?
Чему должна быть равна величина Числу эндогенных переменных Равны между собой (друг другу) и равны 0 (если > одного ответа), а если один ответ, то равны 0) Чему равно количество параметров модели Чему равносилен пропуск значащей объясняющей переменной в эконометрической модели?—Неверному виду функции регрессии Число степеней свободы для уравнения k-мерной регрессии при достаточном числе наблюдений n составляет: n-k-1 Что вычисляется по формуле где и еще возможно ковариационную матрицу оценок коэффициентов функции регрессии, у u2 *(X^T* X)^(-1) ; +стандартную ошибку прогноза (но это все дичь, я не понял смысла вопроса) Что нужно знать для построения интервального прогноза значения эндогенной переменной [ŷ0-, ŷ0+]?: формулы со значениями y = a + bx+u ———— параметры а и b Что принимается за ошибку I типа (рода) + когда отвергается верная гипотеза Н0 и принимается конкурирующая гипотеза Н1; +ошибочное отклонение истинной гипотезы Что следует изменить, если в спецификации вид функции регрессии Что требует тест Голдфелда-Квандта? ESS1, ESS2, F крит +упорядочения уравнений Что принимается за ошибку II типа (рода): 💡 ВидеоCистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать  Математика это не ИсламСкачать  Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать  Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. Практ. ч. 6 класс.Скачать  Линейное уравнение с двумя переменными. 6 класс.Скачать  Алгебра 7 Линейное уравнение с одной переменнойСкачать  Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать  Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать  МЕРЗЛЯК-7. ЛИНЕЙНЫЕ УРАВНЕНИЯ. ПАРАГРАФ-2Скачать  Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать  Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать  Эконометрика Линейная регрессия и корреляцияСкачать  Парная регрессия: линейная зависимостьСкачать  Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать  Линейные уравнения с одной переменной . Алгебра . 7 класс .Скачать  График линейного уравнения с двумя переменными. 6 класс.Скачать  18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать  Множественная регрессияСкачать  |

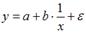
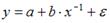


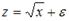














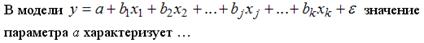





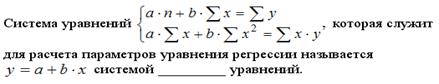




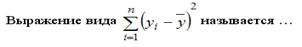
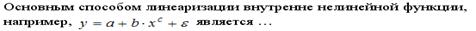



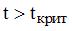


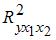


 . Влияние случайных факторов на величину предложения в этой модели учтено посредством случайной величины e
. Влияние случайных факторов на величину предложения в этой модели учтено посредством случайной величины e с помощью метода наименьших квадратов определяют минимальное значение величины :
с помощью метода наименьших квадратов определяют минимальное значение величины :  ,где
,где 

 – фактические значения,
– фактические значения,  – расчетные значения для i-го наблюдения, тогда суть метода наименьших квадратов (МНК) состоит
– расчетные значения для i-го наблюдения, тогда суть метода наименьших квадратов (МНК) состоит


 ?
? параметра
параметра  называется несмещенной, если математическое ожидание
называется несмещенной, если математическое ожидание  »; где
»; где  – истинное значение параметра, вычисленное для генеральной совокупности.
– истинное значение параметра, вычисленное для генеральной совокупности. ; (l=1,2,…,L; j=1,2,…), где l – номер переменной, – количество переменных в рассматриваемой комбинации.
; (l=1,2,…,L; j=1,2,…), где l – номер переменной, – количество переменных в рассматриваемой комбинации. ?—-с размерностью переменной у Свойство неопределенности предусматривает, что
?—-с размерностью переменной у Свойство неопределенности предусматривает, что
 — оценка случайного возмущения (остатков) ui.
— оценка случайного возмущения (остатков) ui.
 и обратная ей
и обратная ей 
 ?
?


 при оценивании эконометрической модели методом наименьших квадратов? ——Нулю Чему должно быть равно количество уравнений эконометрической модели?
при оценивании эконометрической модели методом наименьших квадратов? ——Нулю Чему должно быть равно количество уравнений эконометрической модели? ?
? в рамках парной линейной модели?: коэффициент а1 парной регрессионной модели Что вычисляется по формуле (
в рамках парной линейной модели?: коэффициент а1 парной регрессионной модели Что вычисляется по формуле ( ): коэффициент детерминации Что вычисляется по формуле
): коэффициент детерминации Что вычисляется по формуле  при исследовании качества спецификации линейной эконометрической модели?: фактическое значение Fмод парной регрессии Что вычисляется по формуле:
при исследовании качества спецификации линейной эконометрической модели?: фактическое значение Fмод парной регрессии Что вычисляется по формуле:  ?: статистика Дарбина-Уотсона (DW) Что вычисляется по формуле:
?: статистика Дарбина-Уотсона (DW) Что вычисляется по формуле:  ?: коэффициент корреляции ryx Что из перечисленного необходимо знать для построения оптимального прогноза значения эндогенной переменной,
?: коэффициент корреляции ryx Что из перечисленного необходимо знать для построения оптимального прогноза значения эндогенной переменной,  ?: уравнение регрессии со значениями параметров а0 и а1, среднее значение Х Что измеряет коэффициент детерминации?: показывает долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака (y) или качество регрессионной модели, если проще. Что необходимо знать для проведения оценки точности прогноза значения эндогенной переменной,
?: уравнение регрессии со значениями параметров а0 и а1, среднее значение Х Что измеряет коэффициент детерминации?: показывает долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака (y) или качество регрессионной модели, если проще. Что необходимо знать для проведения оценки точности прогноза значения эндогенной переменной,  ? :
? :


 где
где 

 — это средняя стандартная ошибка прогноза Что оценивается методом наименьших квадратов в уравнении регрессии вида
— это средняя стандартная ошибка прогноза Что оценивается методом наименьших квадратов в уравнении регрессии вида предпосылка
предпосылка  неадекватна?
неадекватна?