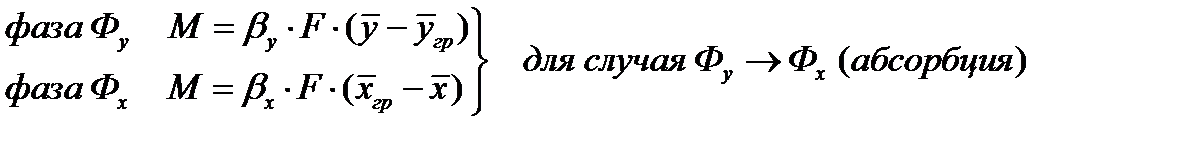В связи со сложностью механизма массоотдачи в практических расчетах используют относительно простое уравнение массоотдачи:
Т.е. скорость массоотдачи (кг/с) пропорциональна межфазной поверхности и средней разности концентраций на этой поверхности и в ядре фазы.
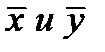
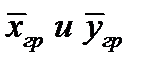
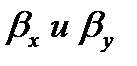
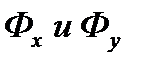
Коэффициент массоотдачи равен количеству вещества, отдаваемого межфазной поверхности в фазу за 1сек. при единичной движущей силе 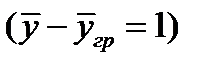
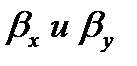
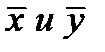
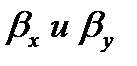
Т.к 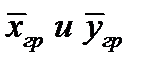
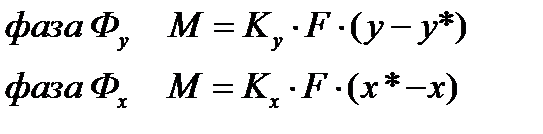
где y * и x * — равновесные концентрации в данной фазе, соответствующие концентрациям в ядре другой фазы; Ky и Kx – коэффициенты массопередачи, соответствующие концентрациям распределяемого вещества в фазах 
Т.е. движущая сила процесса массопереноса, выражающая отклонение системы от равновесия, равна разности рабочей и равновесной концентраций вещества в данной фазе. Размерности коэффициентов массоотдачи и массопередачи одинаковы.
Движущая сила массопереноса – величина переменная, т.к. концентрации изменяются вдоль межфазной поверхности. Поэтому пользуются средней движущей силой:

Из основного уравнения массопередачи обычно определяют F.
Пусть линия равновесия описывается уравнением y * = m∙x, где m – тангенс угла наклона равновесной линии. Тогда коэффициенты массопередачи и массоотдачи связаны уравнениями аддитивности фазовых сопротивлений:

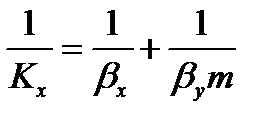
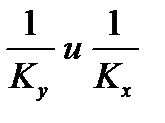
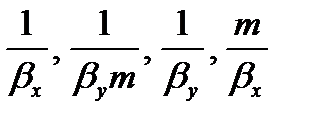
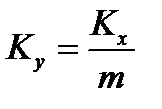
Для кривой линии равновесия m, Kx, Ky изменяются по высоте аппарата. В этом случае используют Кср.
Иногда сопротивление одной из фаз очень мало, и тогда 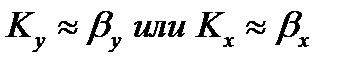
Повысить скорость массопередачи можно увеличением скорости потока той фазы, сопротивление которой больше.
Аддитивность фазовых сопротивлений нарушается при значительном сопротивлении межфазной поверхности.
Основное уравнение массопередачи аналогично основному уравнению теплопередачи: 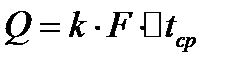
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Лекция № 11 Процесс массопередачи
Массопередача – это сложный процесс, включающий перенос вещества (массы) в пределах одной фазы, перенос через поверхность раздела фаз и его перенос в пределах другой фазы. Как известно, при теплопередаче обменивающиеся теплотой среды в большинстве случаев разделены твердой стенкой, в то время как массопередача происходит обычно через границу раздела соприкасающихся фаз. Эта граница может быть либо подвижной (массопередача в системах газ-жидкость или пар-жидкость, жидкость-жидкость), либо неподвижной (массопередача с твердой фазой).
массоотдача – это перенос вещества из фазы к границе раздела фаз или в обратном направлении, т. е. в пределах только одной фазы.
Виды процессов массопередачи. В промышленности применяются в основном следующие процессы массопередачи:
1. Абсорбция — поглощение газа жидкостью, т. е. процесс разделения, характеризуемый переходом вещества из газовой фазы в жидкую.
2. Экстракция (в системе жидкость-жидкость) — извлечение вещества, растворенного в жидкости, другой жидкостью, практически несмешивающейся или частично смешивающейся с первой. При этом извлекаемый компонент исходного раствора переходит из одной жидкой фазы в другую.
8. Перегонка — разделение гомогенных жидких смесей путем взаимного обмена компонентами между жидкостью и паром, полученным испарением разделяемой жидкой смеси.
4. Адсорбция — поглощение компонента газа, пара или раствора твердым пористым поглотителем, т. е. процесс разделения, характеризуемый переходом вещества из газовой (паровой) или жидкой фазы в твердую.
5. Сушка — удаление влаги из твердых материалов, главным образом путем ее испарения.
6. Кристаллизация — выделение твердой фазы в виде кристаллов из растворов или расплавов.
7. Растворение и экстракция (в системе твердое тело — жидкость).
Процессы массопередачи можно разделить на две группы.
К одной группе относятся процессы (абсорбция, экстракция и др.), в которых участвуют минимально три вещества: одно находится только в одной фазе, другое — только во второй фазе, а третье — переходит из одной фазы в другую и представляет собой распределяемое между фазами вещество.
К другой группе относятся процессы (например, перегонка), в которых вещества, составляющие две фазы, обмениваясь компонентами, сами непосредственно участвуют в массопередаче и уже не могут рассматриваться как инертные носители распределяемого вещества.
Скорость массообменных процессов, как правило, лимитируется молекулярной диффузией. Поэтому процессы массопередачи иногда называют диффузионными процессами.
Равновесие при массопередаче
Правило фаз. Знание равновесия в процессах массопередачи позволяет установить пределы, до которых могут протекать эти процессы. В основе равновесия лежит известное правило фаз:
Видео:Массообменные процессы. Часть 1. Уровень: начальныйСкачать

Ф + С = К + 2, (1)
где Ф — число фаз; С — число степеней свободы, т. е. число независимых переменных, значения которых можно произвольно изменять без нарушения числа или вида (состава) фаз в системе; К — число компонентов системы.
Правило фаз указывает число параметров, которое можно менять произвольно (в известных пределах) при расчете равновесия в процессах масообмена.
Зависимости между независимыми переменными могут быть изображены в плоских координатах в виде так называемых фазовых диаграмм. В расчетах по массопередаче используют диаграммы зависимости давления от концентрации (при t = const), температуры от концентрации (при Р = const) и диаграммы зависимости между равновесными концентрациями фаз, приведенные ниже.
Фазовое равновесие. Линия равновесия. Рассмотрим в качестве примера процесс массопередачи, в котором аммиак, представляющий собой распределяемый компонент, поглощается из его смеси с воздухом чистой водой, т. е. ввиду отсутствия равновесия переходит из газовой фазы Фу, где его концентрация равна у, в жидкую фазу Фх, имеющую начальную концентрацию х = 0. С началом растворения аммиака в воде начнется переход части его молекул в обратном направлении со скоростью, пропорциональной концентрации аммиака в воде и на границе раздела фаз. С течением времени скорость перехода аммиака в воду будет снижаться, а скорость обратного перехода возрастать, причем такой двусторонний переход будет продолжаться до тех пор, пока скорости переноса в обоих направлениях не станут равны друг другу. При равенстве скоростей установится динамическое равновесие, при котором не будет происходить видимого перехода вещества из фазы в фазу.
При равновесии достигается определенная зависимость между предельными или равновесными концентрациями распределяемого вещества в фазах для данных температуры и давления, при которых осуществляется процесс массопередачи.
В условиях равновесия некоторому значению 





Отношение концентраций фаз при равновесии называется коэффициентом распределения 
Конкретный вид законов равновесного распределения различен для разных процессов массопередачи. Так, например, в процессе абсорбции при низких концентрациях распределяемого вещества в исходном растворе равновесие описывается законом Генри для идеальных растворов в процессах ректификации — законом Рауля и т. д.
Зная линию равновесия для конкретного процесса и рабочие, т. е. неравновесные, концентрации фаз в соответствующих точках, можно определить направление и движущую силу массопередачи в любой точке аппарата. На основе этих данных может быть рассчитана средняя движущая сила, а по ней — скорость процесса массопередачи.

Зависимость между рабочими концентрациями распределяемого вещества в фазах 

Рассмотрим схему массообменного аппарата, работающего в режиме идеального вытеснения при противотоке фаз (рис. 2). Пусть в процессе массопередачи из фазы в фазу, например из газовой фазы в жидкую, переходит только один распределяемый компонент (скажем, аммиак).
Сверху в аппарат поступает Lн кг/с одной фазы (жидкой), содержащей 





Тогда материальный баланс по всему веществу

и материальный баланс по распределяемому компоненту

Теперь напишем уравнения материального баланса для части аппарата от его нижнего конца до некоторого произвольного сечения, для которого расходы фаз составляют G и L кг/с, а их текущие концентрации равны 

Материальный баланс по всему веществу

и материальный баланс по распределяемому компоненту

Решая это уравнение относительно 

Уравнение (7) представляет собой уравнение рабочей линии, выражающее связь между рабочими концентрациями распределяемого компонента в фазах для произвольного сечения аппарата.
Расходы фаз постоянны по высоте аппарата, например в процессах ректификации, когда числа молей компонентов, которыми обмениваются фазы, равны. В других случаях, если концентрации фаз мало изменяются по высоте аппарата, то расходы фаз по его высоте можно с достаточной для практических целей точностью считать постоянными, т. е. принять L = const и G = const. При этом Lк = L, Gн = G и уравнение (7) приводится к виду

Вводя обозначения 


Выражения (8) и (9) являются уравнениями рабочей линии, которыми обычно пользуются при расчетах массообменных процессов.
Таким образом, рабочая линия представляет собой прямую, которая наклонена к горизонту под углом, тангенс которого равен А, и отсекает на оси ординат отрезок, равный В. Рабочая линия для всего аппарата ограничена точками с координатами 



Скорость массопередачи
Скорость массопередачи связана с механизмом переноса распределяемого вещества в фазах между которыми происходит массообмен.
Перенос вещества внутри фазы может происходить только путем молекулярной диффузии либо путем конвекции и молекулярной диффузии одновременно. Посредством одной молекулярной диффузии вещество перемещается, строго говоря, лишь в неподвижной среде. В движущейся среде перенос вещества осуществляется как молекулярной диффузией, так и самой средой в направлении ее движения или отдельными ее частицами в разнообразных направлениях.
В турбулентном потоке перенос молекулярной диффузией преобладает только вблизи границы фазы. При турбулентном течении возникают нерегулярные пульсации скорости, под действием которых, наряду с общим движением потока, происходит перемещение частиц во всех направлениях, в том числе и в поперечном.
Конвективный перенос вещества, осуществляемый под действием турбулентных пульсаций, часто называют турбулентной диффузией.
Молекулярная диффузия. Молекулярной диффузией называется перенос распределяемого вещества, обусловленный беспорядочным тепловым движением молекул, атомов, ионов, коллоидных частиц. Молекулярная диффузия описывается первым законом Ф и к а, согласно которому масса вещества dМ, продиффундировавшего за время dt через элементарную поверхность dF (нормальную к направлению диффузии), пропорциональна градиенту концентрации этого вещества


Из выражения (1) следует, что удельный поток вещества, переносимого молекулярной диффузией через единицу поверхности (F = 1) в. единицу времени (t = 1), или скорость молекулярной диффузии, составляет

По своей структуре закон Фика аналогичен закону Фурье, описывающему передачу тепла теплопроводностью, причем аналогом градиента температур является в данном случае градиент концентраций, представляющий собой изменение концентрации диффундирующего вещества на единицу длины нормали между двумя поверхностями постоянных, но различных концентраций.
Коэффициент пропорциональности D в выражении закона Фика называется коэффициентом молекулярной диффузии, или просто коэффициентом диффузии. Знак минус перед правой частью первого закона Фика указывает на то, что молекулярная диффузия всегда протекает в направлении уменьшения концентрации распределяемого компонента.
Согласно уравнению (1), коэффициент диффузии выражается как:
откуда (до сокращения одноименных величин) вытекает физический смысл D. Коэффициент диффузии, показывает, какая масса вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице.
Коэффициент молекулярной диффузии представляет собой физическую константу, характеризующую способность данного вещества проникать вследствие диффузии в неподвижную среду. Величина D таким образом не зависит от гидродинамических условий, в которых протекает процесс.
Турбулентная диффузия. Масса вещества dMт, переносимого в пределах фазы вследствие турбулентной диффузии, может быть принята, по аналогии с молекулярной диффузией, пропорциональной поверхности dF, времени dt и градиенту концентрации 

где 
Коэффициент турбулентной диффузии 
Коэффициент 

Конвективный перенос. Скорость конвективного, переноса вещества вместе с самой средой в направлении, совпадающем с направлением общего потока, равна

где v — скорость потока жидкости, газа или пара; С — коэффициент пропорциональности.
Суммарный перенос вещества вследствие конвективного переноса и молекулярной диффузии, по аналогии с теплообменом, называют конвективным массообменом или конвективной диффузией.
Распределение концентрации при переносе путем конвективной диффузии определяется в самом общем виде дифференциальным уравнением конвективной диффузии.
Дифференциальное уравнение конвективной диффузии. Выделим в потоке данной фазы элементарный параллелепипед с ребрами dx, dy и dz, ориентированными относительно осей координат, как показано на рис. 1. Рассмотрим материальный баланс по распределяемому веществу для параллелепипеда в наиболее общем случае неустановившегося массообмена. Будем считать, что процесс переноса происходит в условиях установившегося движения потока фазы. Распределяемое вещество проходит сквозь грани параллелепипеда как путем конвективного переноса, так и молекулярной диффузии.
Обозначим концентрацию распределяемого вещества в плоскости левей грани параллелепипеда площадью dydz через с и проекции скорости на оси координат для данного элемента (точки) потока — через 


Тогда масса вещества, поступающего только путем конвективной диффузии через площадь dydz, т. е. в направлении оси х, за время dt составит

На противоположной грани параллелепипеда скорость в направлении оси х равна 


Разность между массами вещества, прошедшего через противоположные грани параллелепипеда за время dt в направлении оси х, равна

где dV = dx dy dz — объем элементарного параллелепипеда. Аналогично в направлении осей у и z:


Таким образом, содержание распределяемого вещества в объеме параллелепипеда изменится за время dt вследствие перемещения вещества только путем конвективной диффузии на величину
или в развернутом виде

Согласно уравнению неразрывности потока для установившегося движения фазы

Следовательно, предыдущее выражение dMк примет вид

Масса распределяемого вещества, поступающего в параллелепипед только путем молекулярной диффузии через грань dy dz за время dt составляет

Масса вещества, выходящего за то же время путем молекулярной диффузии через противоположную грань,

Разность между массами продиффундировавшего через противоположные грани параллелепипеда вещества в направлении оси х за время dt равна

Аналогично в направлении осей у и z:


Масса распределяемого вещества в объеме всего параллелепипеда за время dt изменится при переносе путем молекулярной диффузии на величину

В результате изменение массы распределяемого вещества во времени в объеме параллелепипеда

Изменение массы распределяемого вещества за счет конвективной и молекулярной диффузии в объеме параллелепипеда по закону сохранения массы должно равняться соответствующему изменению массы этого вещества во времени, т. е.

Проводя соответствующие сокращения и перегруппировывая члены этого уравнения, получим


или в более краткой записи

Уравнение (20) представляет собой дифференциальное уравнение конвективной диффузии. Оно выражает закон распределения концентрации данного компонента в движущейся стационарно среде при неустановившемся процессе массообмена.
Уравнение (20) по структуре аналогично дифференциальному уравнению конвективного теплообмена (уравнению Фурье-Кирхгофа). Отличие состоит в том, что в уравнение (20) вместо температурного градиента входит градиент концентрации, а вместо коэффициента температуропроводности а — коэффициент молекулярной диффузии D.
Для частного случая установившегося массообмена уравнение (20) принимает вид:

При массообмене в неподвижной среде 



Уравнение (22) носит название второго закона Фика. В дифференциальном уравнении конвективной диффузии, помимо концентрации, переменной является скорость потока. Поэтому данное уравнение надо рассматривать совместно с дифференциальными уравнениями гидродинамики: уравнениями Навье-Стокса и уравнением неразрывности потока. Однако эта система уравнений не имеет аналитического решения, и для получения расчетных зависимостей по массообмену приходится прибегать к преобразованию дифференциального уравнения конвективной диффузии методами теории подобия.
Ввиду сложности механизма процессов массоотдачи в фазах для практических целей принимают, что скорость массоотдачи пропорциональна движущей силе, равной разности концентраций в ядре и на границе фазы или (в случае обратного направления переноса) разности концентраций на границе и в ядре фазы. Соответственно, если распределяемое вещество переходит из фазы Фу в фазу Фх, то основное уравнение массоотдачи, определяющее количеством М вещества, переносимого в единицу времени в каждой из фаз (к границе фазы или в обратном направлении), выражается следующим образом:


входящие в эти уравнения разности концентраций 





Коэффициенты пропорциональности в уравнениях (1) и (1, а) называются коэффициентами массоотдачи. Коэффициенты массоотдачи 

Коэффициент массоотдачи является не физической константой, а кинетической характеристикой, зависящей от физических свойств фазы (плотности, вязкости и др.) и гидродинамических условий в ней (ламинарный или турбулентный режим течения), связанных в свою очередь с физическими свойствами фазы, а также с геометрическими факторами, определяемыми конструкцией и размерами массообменного аппарата, Таким образом, величина 
По своему смыслу коэффициент массоотдачи является аналогом коэффициента теплоотдачи в процессах переноса тепла, а основное уравнение массоотдачи идентично по структуре основному уравнению теплоотдачи.
Коэффициент массоотдачи может быть выражен в различных единицах в зависимости от выбора единиц для массы распределяемого вещества и движущей силы. Если принять, что масса вещества выражена в килограммах, то в общей форме коэффициент массоотдачи выразится следующим образом:
При этом единица измерения р в каждом конкретном случае будет связана с единицами, принятыми для выражения движущей силы (табл. Х-1).
Подобие процессов переноса массы. Наиболее строгий и принципиально возможный путь для определения коэффициентов массоотдачи, заключается в интегрировании уравнения диффузии в движущейся среде (Х,19) совместно с уравнениями движения, т. е. с уравнениями Навье-Стокса и уравнением неразрывности потока при заданных начальных и граничных условиях.
Однако система указанных уравнений практически не имеет общего решения. Поэтому так же, как для гидродинамических и теплообменных процессов, не решая системы основных уравнений, можно методами теории подобия найти связь между переменными, характеризующими процесс переноса в потоке фазы, в виде обобщенного (критериального) уравнения массоотдачи.
Общая функциональная зависимость Nu’ от определяющих критериев и симплексов подобия для неустановившихся процессов массоотдачи может быть выражена как

Для установившихся процессов массоотдачи условие равенства критериев Fo’ в сходственных точках подобных потоков отпадает н приведенные выше обобщенные зависимости принимают вид:

Расчетная зависимость типа уравнения (13 и 14) называется обобщенным или критериальным уравнением массоотдачи.
Как отмечалось, процесс массопередачи включает процессы массоотдачи в пределах каждой из двух взаимодействующих фаз и, кроме того, процесс переноса распределяемого вещества через поверхность раздела фаз. Сложность расчета процесса связана с тем, что практически невозможно измерить концентрации фаз непосредственно у границы их раздела. Учитывая это, основное уравнение массопередачи, определяющее массу М вещества, переносимого из фазы в фазу в единицу времени (нагрузку аппарата), выражают следующим образом:


где у*, х* — равновесные концентрации в данной фазе, соответствующие концентрациям распределяемого вещества в основной массе (ядре) другой фазы; Ку, Кх— коэффициенты и массопередачи, выраженные соответственно через концентрации фаз Фу и Фх.
Коэффициент массопередачи (Kу или Кх) показывает, какая масса вещества переходит из фазы в фазу за единицу времени через единицу поверхности контакта фаз при движущей силе массопередачи, равной единице.
По физическому смыслу коэффициенты массопередачи отличаются от коэффициентов массоотдачи, но выражены в одинаковых с ними единицах измерения. Таким образом, коэффициенты массопередачи могут выражаться в м/с, кг/(м2 с); кг/(м2 с мол доли) и в с/м.
Концентрации фаз изменяются при их движении вдоль поверхности раздела, соответственно изменяется движущая сила массопередачи. Поэтому в уравнение массопередачи вводят величину средней движущей силы ( 



С помощью уравнений (3) и (4) обычно находят поверхность контакта фаз F и по ней рассчитывают основные размеры аппарата. Для определения F необходимо предварительно рассчитать коэффициент массопередачи Kу или Кх и среднюю движущую силу. Величина М либо задается при расчете, либо определяется из материального баланса.
Зависимость между коэффициентами массопередачи и массоотдачи. Чтобы установить связь между коэффициентом массопередачи и коэффициентами массоотдачи, обычно принимают, что да границе раздела фаз см. рис. 5) достигается равновесие. Это предположение равносильно допущению о том, что сопротивлением переносу через границу раздела фаз можно пренебречь. Отсюда вытекает, как следствие, положение об аддитивности фазовых сопротивлений, которое является одной из предпосылок для расчета коэффициента массопередачи. Допустим, что распределяемое вещество переходит из фазы Фу в фазу Фх, и движущая сила массопередачи выражается в концентрациях фазы Фу. При установившемся процессе массопередачи количество вещества, переходящее из фазы в фазу, определим по уравнению (1).
Для упрощения рассмотрим случай, когда равновесная зависимость % между концентрациями в фазах линейна, т. е. линия равновесия описывается уравнением у* = m x, где т – тангенс угла наклона линии равновесия. После ряда преобразований получаем

При выражении коэффициента массопередачи в концентрациях фазы Фх аналогичные рассуждения приводят к зависимости

Левые части уравнений (9) и (10) представляют собой общее сопротивление переносу вещества из фазы в фазу, т. е. сопротивление массопередаче, а их правые части — сумму сопротивлений массоотдаче в фазах. Поэтому зависимости (9) и (10) являются уравнениями аддитивности фазовых сопротивлений.
При т = const уравнение (10) можно получить, разделив уравнение (9) на т. Отсюда следует, что величины Kу и Kх связаны зависимостью Kу = Kх/m.
Уравнения аддитивности (9) и (10) выведены для линейной равновесной зависимости, но они остаются в силе и для кривой линии равновесия.
Видео:СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

КОНВЕКЦИЯ И МАССООТДАЧА
Под конвективным массопереносом понимают процесс переноса вещества при движении жидкости иди газа. Этот процесс происходит как бы механически -макрообъемными частицами жидкостного или газового потока.
Рассмотрим некоторые вопросы переноса массы внутри одной фазы, т.е. от ядра потока к границе раздела фаз или наоборот -от границы раздела фаз в ядро потока. Полагаем, что в нашем случае процесс массопереноса происходит между газом и жидкостью (процесс абсорбции, т.е. массоперенос идет из фазы Фу в фазу Фх), режим движения турбулентный.
Гидродинамические особенности турбулентного потока в канале были рассмотрены в гл. 3. Здесь же следует отметить влияние гидродинамических условий на перенос вещества. В пограничном слое толщиной δr (рис. 15-2) происходит резкое, близкое к линейному изменение концентраций; поскольку в этой области потока скорость процесса определяется молекулярной диффузией, роль конвективной диффузии мала. Это объясняется тем, что на границе раздела фаз усиливается тормозящее действие сил трения между фазами и сил поверхностного натяжения на границе жидкой фазы. Образование гидродинамического пограничного слоя вблизи поверхности раздела фаз ведет к возникновению в нем диффузионного пограничного слоя толщиной δД, обычно не совпадающей с δr. В ядре потока массоперенос осуществляется в основном турбулентными пульсациями, поэтому концентрация распределяемого вещества в ядре потока практически постоянна. Как отмечалось выше, перенос вещества движущимися частицами, участвующими в турбулентных пульсациях, называют турбулентной диффузией. Перенос вещества турбулентной диффузией описывается уравнением, аналогичным уравнению (15.14а):
где U —средняя пульсационная скорость движения частицы жилкости в поперечном направлении; l-расстояние, на которое перемещаются частицы в поперечном направлении; ɛд = Ul —коэффициент турбулентной диффузии.
Рис. 15-2. Профили изменения скорости потока жидкой фазы (w) и концентрации растворенного вещества (х) в турбулентном потоке
Очевидно, что пограничный слой создает основное сопротивление процессу переноса.
Перенос по рассмотренной схеме называют массоотдачей. По мере приближения к ламинарному режиму пограничный слой сильно разрастается, как бы заполняя все сечение потока. В этих условиях конвективный перенос идет в направлении, параллельном движению потока. При этом перенос массы к границе раздела определяется в основном молекулярной диффузией. Очевидно, что скорость конвективного переноса существенно выше скорости молекулярной диффузии. Поэтому развитие турбулентности способствует ускорению конвективного переноса массы.
Теоретическим путем толщину пограничного диффузионного слоя можно определить для самых простых случаев массопереноса. Поэтому использование первого закона Фика
для описания процесса затруднительно, так как закон распределения концентраций в пограничном слое (дс/дп) неизвестен.

По аналогии с эмпирическим законом охлаждения Ньютона (или уравнением теплоотдачи) уравнение массоотдачи имеет следующий вид:
где bx -коэффициент пропорциональности коэффициент массоотдачи.
При установившемся процессе для всей поверхности F массоотдачи при τ = 1 с уравнение (15.18) принимает вид
Для фазы Ф уравнение массоотдачи будет аналогично уравнению (15.18а), но с соответствующей заменой концентраций:
Из уравнений (15.18) и (15.19) найдем размерность коэффициентов массоотдачи:

Коэффициент массоотдачи показывает, какое количество вещества переходит от единицы поверхности раздела фаз в ядро потока (или наоборот) в единицу времени при движущей силе, равной единице.
Коэффициент массоотдачи, в отличие от коэффициента массопередачи, характеризует скорость переноса вещества внутри фазы конвекцией и молекулярной диффузией одновременно. Коэффициент массоотдачи зависит от многих факторов (физических свойств фазы, скорости потока, определяющих геометрических размеров и т.д.) и является аналогом коэффициента теплоотдачи. Ввиду сложной зависимости коэффициента массоотдачи от этих факторов получение обобщенной зависимости для определения величины by или bx крайне затруднительно.
При разработке моделей массопереноса обычно принимают допущение о том, что на поверхности раздела фазы находятся в состоянии равновесия, а общее сопротивление процессу переноса складывается из суммы сопротивлений двух фаз. Из этих допущений следует, что на границе раздела фаз отсутствует сопротивление процессу (т. с. равновесие на границе устанавливается очень быстро -во всяком случае, быстрее изменения средней концентрации в ядре фазы, что для ряда процессов массопереноса доказано экспериментально) и что процесс массопереноса подчиняется правилу аддитивности фазовых сопротивлений.
Вследствие взаимного влияния движения фаз, участвующих в процессе массопереноса, математическое описание скорости процесса чрезвычайно сложно. Поэтому решение дифференциальных уравнений переноса (см. гл. 3) оказывается возможным лишь в простейших случаях, когда точно известна поверхность контакта фаз и, как правило, при их ламинарном движении. В этом случае скорость процесса определяют совместным решением уравнений переноса в каждой из фаз.
Пленочная (двухпленочная) модель Льюиса и Уитмена основана на предпосылках, ранее рассмотренных Нернстом при изучении им растворения твердых тел в жидкостях. По этой модели с обеих сторон поверхности контакта фаз образуются неподвижные или ламинарно движущиеся пленки, в которых перенос вещества осуществляется только молекулярной диффузией. Эти пленки отделяют поверхность контакта фаз от ядра потока, в котором концентрация практически постоянна; все изменения концентрации вещества происходят в пленке.
В соответствии с пленочной моделью интегрирование уравнении (15.14а) приводит к выражению
где δпл -толщина пленки; с0 и сгр -средняя концентрация в ядре фазы и концентрация на границе раздела фаз соответственно.
Сравнивая последнее уравнение с уравнениями (15.18) и (15.19), получим
Из уравнения (15.21) следует, что величина Р обратно пропорциональна толщине пленки, которая определяется гидродинамическими условиями: чем более турбулентны фазы, тем меньше δпл и, следовательно, тем выше b.
Уравнение (15.21) также показывает, что по пленочной модели коэффициент массоотдачи линейно зависит от коэффициента диффузии, что часто не подтверждается экспериментально. Кроме того, эта теория не учитывает деформации поверхности контакта фаз и переноса вещества турбулентными пульсациями.
Рис. 15-3. К пояснению медали пограничного диффузионного слоя.
В модели пограничного диффузионного слоя, которую можно считать дальнейшим развитием пленочной модели, отражено влияние гидродинамических условий на процесс массопереноса. По этой модели (рис. 15-3) кончен фация вещества, постоянная в ядре потока, в турбулентном подслое толщиной δг, постепенно снижается при приближении к тираничному слою (т.е. в буферном подслое), в котором соизмеримы молекулярные и турбулентные силы вязкости, т.е. v ≈ vт. С уменьшением масштаба пульсаций в вязком подслое толщиной 6, концентрация снижается существенно быстрее. В глубине вязкого подслоя, внутри тонкого диффузионного подслоя толщиной δд молекулярный перенос становится основным, при этом v » vт. Толщина пограничного диффузионного слоя δд меньше толщины вязкого пограничного слоя δг , причем
где m — показатель степени, отражающий закон затухания турбулентного переноса вблизи границы раздела фаз.
Для систем жидкость -твердое тело m = 3, а для систем газ(пар) -жидкость и жидкость-жидкость m = 2. Поэтому [из уравнений (15.20) и (15.22)] для систем твердое тело-жидкость М
D 0,66 , а для систем газ(нар)-жидкость и жидкость-жидкость М
Модель обновления поверхности фазового контакта часто называют моделью проницания, или пенетрационной. По этой модели предполагается, что турбулентные пульсации постоянно подводят к поверхности раздела фаз свежую жидкость и смывают порции жидкости, уже прореагировавшей с газом (паром), т.е. каждый элемент поверхности жидкости взаимодействует с газом (паром) в течение некоторого времени τ (время контакта или обновления), после чего данный элемент обновляется. На основе этой модели, принимая время т контакта постоянным для всех элементов поверхности, Хигби получил уравнение для определения коэффициента массоотдачи:
🎥 Видео
Решение биквадратных уравнений. 8 класс.Скачать

Уравнение из МФТИ Эпичный косякСкачать

Массопередача лекция 3Скачать

Математика без Ху!ни. Уравнение касательной.Скачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Уравнение касательнойСкачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

7.5 ЧАСОВ МАТАНА!!! ПОДАРОК ВСЕМ СТУДЕНТАМ ДЛЯ ПОДГОТОВКИ К ЗАЧЁТАМ И ЭКЗАМЕНАМ ОТ ЁЖИКА В МАТАНЕ!!!Скачать

✓ Суперсложная экономическая задача | В интернете кто-то неправ #031 | Проφиматика и Борис ТрушинСкачать

Основы массорепедачи. Первая лекцияСкачать

Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Геометрический смысл производной. Уравнение касательнойСкачать

Расчет выхода продукта от теоретически возможного. 10 класс.Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Теплоотдача и теплопередача.Скачать