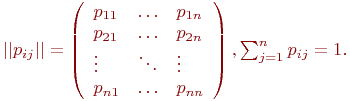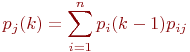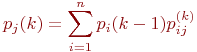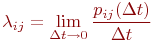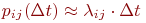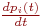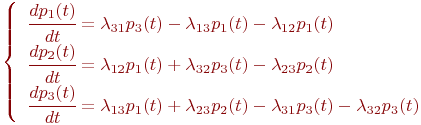Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова — старшего (1856 — 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
Марковские процессы делятся на два класса:
· дискретные марковские процессы (марковские цепи);
· непрерывные марковские процессы.
Дискретной марковской цепьюназывается случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.
Непрерывным марковским процессомназывается случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.
Система 
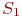
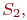
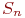
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 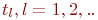
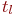
Известны вероятности перехода 

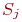
Цель моделирования: определить вероятности состояний системы после 
Обозначим эти вероятности 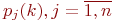

Если в системе отсутствует последействие, то есть вероятности 

Марковская цепь называется однородной, если переходные вероятности 
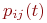
Значения 
Значения 
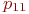
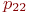
Не указываются также нулевые вероятности переходов. Например, на рис. это вероятности 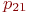
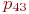
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
где 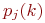
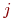

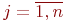
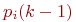
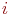

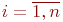
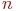

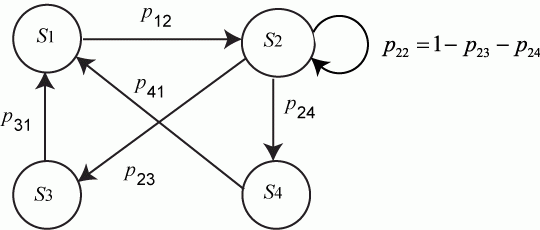
Рис.Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
где 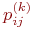

Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то — занятость. Если состояния объектов, то — поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости определить искомые вероятности.
В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей 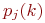
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 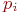

Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 
где 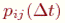


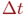
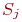
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов 

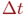
Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы 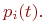
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
1. Определить состояния системы и плотности вероятностей переходов 
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части уравнения записывается производная вероятности 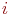
5. В правой части записывается алгебраическая сумма произведений 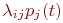
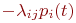
6. Определить начальные условия и решить систему дифференциальных уравнений.
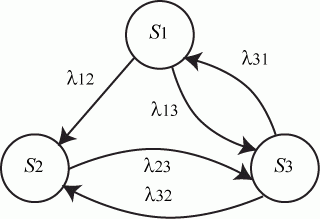
Пример. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рисунке.
Рис. Размеченный граф состояний
Очевидно, 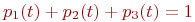
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера можно задать такие начальные условия: 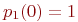
Дата добавления: 2015-04-03 ; просмотров: 7905 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:03 Марковские процессы с дискретным временемСкачать
Марковские цепи уравнение колмогорова чепмена
М арковские процессы принятия решений
8.1. Основные понятия марковских процессов
Как указывалось выше, одним из важнейших факторов, который должен учитываться в процессе принятия оптимальных решений, является фактор случайности. Следует отметить при этом, что упомянутый выше фактор «неопределенности» не адекватен фактору «случайности», так как при учете «случайности» необходимо, чтобы массовые случайные явления обладали свойством статической устойчивости . Это означает, что учитываемые случайные явления подчиняются определенным статическим закономерностям, требования которых не обязательны при учете неопределенности.
Условие статической устойчивости позволяет использовать в процессе принятия решений эффективные математические методы теории случайных процессов и, в частности, одного из ее разделов — теории марковских процессов.
Марковские случайные процессы названы по имени выдающегося русского математика А.А.Маркова (1856-1922), впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать «динамикой вероятностей». В дальнейшем основы этой теории явились исходной базой общей теории случайных процессов, а также таких важных прикладных наук, как: теория диффузионных процессов, теория надежности, теория массового обслуживания и т.д. В настоящее время теория марковских процессов и ее приложения широко применяются в самых различных областях таких наук, как механика, физика, химия и др.
Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений, особое внимание марковские процессы приобрели у специалистов, занимающихся исследованием операций и теорией принятия оптимальных решений.
Несмотря на указанную выше простоту и наглядность, практическое применение теории марковских цепей требует знания некоторых терминов и основных положений, на которых следует остановиться перед изложением примеров.
Как указывалось, марковские случайные процессы относятся к частным случаям случайных процессов (СП). В свою очередь, случайные процессы основаны на понятии случайной функции (СФ).
Случайной функцией называется функция, значение которой при любом значении аргумента является случайной величиной (СВ). По иному, СФ можно назвать функцию, которая при каждом испытании принимает какой-либо заранее неизвестный вид.
Такими примерами СФ являются: колебания напряжения в электрической цепи, скорость движения автомобиля на участке дороги с ограничением скорости, шероховатость поверхности детали на определенном участке и т.д.
Как правило, считают, что если аргументом СФ является время, то такой процесс называют случайным . Существует и другое, более близкое к теории принятия решений, определение СП. При этом под случайным процессом понимают процесс случайного изменения состояний какой-либо физической или технической системы по времени или какому-либо другому аргументу.
Нетрудно заметить, что если обозначить состояние S i и изобразить зависимость S i (t), то такая зависимость и будет случайной функцией .
СП классифицируются по видам состояний S i и аргумента t. При этом СП могут быть с дискретными или непрерывными состояниями или временем. Например, любой выборочный контроль продукции будет относиться к СП с дискретными состояниями (S 1 — годная, S 2 — негодная продукция) и дискретным временем (t 1 , t 2 — времена проверки). С другой стороны, случай отказа любой имашины можно отнести к СП с дискретными состояниями, но непрерывным временем. Проверки термометра через определенное время будут относиться к СП с непрерывным состоянием и дискретным временем. В свою очередь, например, любая осцилограмма будет записью СП с непрерывными состояниями и временем.
Кроме указанных выше примеров классификации СП, существует еще одно важное свойство. Это свойство описывает вероятностную связь между состояниями СП. Так, например, если в СП вероятность перехода системы в каждое последующее состояние зависит только от предыдущего состояния, то такой процесс называется процессом без последействия (рис.8.1):
Рис.8.1. Схема процесса без последействия
Зависимость P i/i+1 = f(S i ) называют переходной вероятностью , часто говорят, что именно процесс без последействий обладает марковским свойством, однако, строго говоря, здесь есть одна неточность. Дело в том, что можно представить себе СП, в котором вероятностная связь существует не только с предшествующими, но и более ранними — S i-1 , S i+2 . состояниями, т.е.
P i/i+1 = f (S i , S i-1 , S i-2 ) (8.1)
Такие процессы также рассматривались А.А.Марковым, который предложил называть их в отличие от первого случая (простой цепи) — сложной цепью. В настоящее время теория таких цепей разработана слабо и обычно применяют так называемый процесс укрупнения состояний путем математических преобразований, объединяя предшествующие состояния в одно.
Это обстоятельство должно обязательно учитываться при составлении математических моделей принятия решений.
Выше мы совершили незаметный терминологический переход от понятия СП к «марковской цепи». Теперь эту неясность следует устранить. Отметим, во-первых, что случайный процесс с дискретными состояниями и временем называется случайной последовательностью .
Если случайная последовательность обладает марковским свойством, то она называется цепью Маркова .
С другой стороны, если в случайном процессе состояния дискретны, время непрерывно и свойство последействия сохраняется, то такой случайный процесс называется марковским процессом с непрерывным временем .
Марковский СП называется однородным , если переходные веро-ятности P i/i+1 остаются постоянными в ходе процесса.
Цепь Маркова считается заданной, если заданы два условия:
1. Имеется совокупность переходных вероятностей в виде матрицы:
2. Вектор начальных вероятностей
P (0) = 01 , P 02 . P 0n > , (8.3)
описывающий начальное состояние системы.
Матрица (2) называется переходной матицей (матрицей перехода). Элементами матрицы являются вероятности перехода из i-го в j-е состояние за один шаг процесса. Переходная матрица (8.2) обладает следующими свойствами:
a) » С P ij і 0 , (8.3)
Матрица, обладающая свойством (8.3), называется стохастической .
Кроме матричной формы модель марковской цепи может быть представлена в виде ориентированного взвешенного графа (рис. 8.2).
Рис.8.2. Ориентированных взвешенный граф
Вершины графа обозначают состояние S i , а дуги — переходные вероятности.
Множество состояний системы марковской цепи определенным образом классифицируются с учетом дальнейшего поведения системы:
1. Невозвратное множество ( рис. 8.3)
Рис. 8.3. Невозвратное множество
В случае невозвратного множества возможны любые переходы внутри этого множества. Система может покинуть это множество, но не может вернуться в него.
2. Возвратное множество (рис. 8.4)
Рис. 8.4. Возвратное множество
В этом случае также возможны любые переходы внутри множества. Система может войти в это множество, но не может покинуть его.
3. Эргодическое множество (рис. 8.5)
Рис. 8.5. Эргодическое множество
В случае эргодического множества возможны любые переходы внутри множества, но исключены переходы из множества и в него.
Поглощающее множество (рис. 8.6)
Рис. 8.6. Поглощающее множество
При попадании системы в это множество процесс заканчивается.
Кроме описанной выше классификации множеств различают состояния системы:
а) существенное состояние (рис.8.7): возможны переходы из S i в S j и обратно
Рис. 8.7. Существенное состояние
б) несущественное состояние (рис. 8.8): возможен переход из S i в S j , но невозможен обратный.
Рис. 8.8. Несущественное состояние
В некоторых случаях, несмотря на случайность процесса, имеется возможность до определенной степени управлять законами распределения или параметрами переходных вероятностей. Такие марковские цепи называются управляемыми . Очевидно, что с помощью управляемых цепей Маркова (УЦМ) особенно эффективным становится процесс принятия решений, о чем будет сказано впоследствии.
Как указывалось выше, основным признаком ДМЦ является детерминированность временных интервалов между отдельными шагами (этапами) процесса. Однако, часто в реальных процессах это свойство не соблюдается и интервалы оказываются случайными с каким-либо законом распределения, хотя марковость процесса сохраняется. Такие случайные последовательности называются полумарковскими .
Кроме того, с учетом наличия и отсутствия тех или иных, упомянутых выше, множеств состояний, марковские цепи могут быть поглощающими , если имеется хотя бы одно поглощающее состояние, или эргодическими , если переходные вероятности образуют эргодическое множество.
В свою очередь, эргодические цепи могут быть регулярными или циклическими . Циклические цепи отличаются от регулярных тем, что в процессе переходов через определенное количество шагов (цикл) происходит возврат в какое-либо состояние. Регулярные цепи этим свойством не обладают. Если просуммировать все вышесказанные определения, то можно дать следующую классификацию марковских цепей (рис. 8.9):
Рис. 8.9. Классификация марковских цепей
8.2. Математический аппарат дискретных марковских цепей
В дальнейшем рассматриваются простые однородные марковские цепи с дискретным временем. Основным математическим соотношением для ДМЦ является уравнение, с помощью которого определяется состояние системы на любом к-том ее шаге. Это уравнение имеет вид:
П [ n ] = P n > * П [ n ] (8.4)
и называется уравнением Колмогорова-Чепмена .
Уравнение Колмогорова-Чепмена относится к классу рекуррентных соотношений, позволяющих вычислить вероятность состояний марковского случайного процесса на любом шаге (этапе) при наличии информации о предшествующих состояниях.
Дальнейшие математические соотношения зависят от конкретного вида марковской цепи.
8.2.1. Поглощающие марковские цепи
Как указывалось выше, у поглощающих ДМЦ имеется множество, состоящее из одного или нескольких поглощающих состояний.
Для примера рассмотрим переходную матрицу, описывающую переходы в системе, имеющей 4 возможных состояния, два из которых являются поглощающими. Матрица перехода такой цепи будет иметь вид:
Практически важным является вопрос о том, сколько шагов сможет пройти система до остановки процесса, то есть поглощения в том или ином состоянии.Для получения дальнейших соотношений путем переименования состояний матрицу (8.5) переводят к блочной форме:
Такая форма позволяет представить матрицу (8.6) в каноническом виде:
где — единичная матрица;
— матрица, описывающая переходы в системе из невозвратного множества состояний в поглощающее множество;
— матрица, описывающая внутренние переходы в системе в невозвратном множестве состояний.
На основании канонической формы (8.6а) получена матрица, называемая фундаментальной .
M [2] = ( I [2] — Q [2] ) -1 , (8.7)
В матрице (8.7) символ ( -1 ) означает операцию обращения, то есть
После соответствующих преобразований матрица (8.7) примет вид:
Каждый элемент матрицы (8.7а) соответствует среднему числу раз попадания системы в то или иное состояние до остановки процесса (поглощения).
Если необходимо получить общее среднее количество раз попадания системы в то или иное состояние до поглощения, то фундаментальную матрицу М необходимо умножить справа на вектор-столбец, элементами которого будут единицы, то есть
Для иллюстрации приведем конкретный числовой пример: пусть известны значенияпереходных вероятностей матрицы П [3] с одним поглощающим состоянием: P 11 = 1; P 12 = P 13 = 0; P 21 = 0,25; P 22 = 0,5; P 23 = 0,25; P 31 = 0,5; P 32 = 0,5; P 33 = 0.
Переходная матрица в блочной системе будет выглядеть так:
В данном случае
Проделаем необходимые вычисления:
В данном случае компоненты вектора М S означают, что если процесс начался с состояния S 2 , общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния S 3 , то — 2,26.
В конкретных задачах, конечно, более информативным результатом будет не количество шагов, а какие-либо временные или экономические показатели. Этот результат легко получить, если связать пребывание в каждом состоянии с соответствующими характеристиками. Очевидно, набор этих характеристик составит вектор, на который нужно умножить М S слева.
Так, если задать в нашем примере время пребывания в состоянии S 2 t 2 = 20 час, а в состоянии S 3 — t 3 = 30 час, то общее время до поглощения будет равно:
В случаях, когда марковская цепь включает несколько поглощающих состояний, возникают такие вопросы: в какое из поглощающих состояний цепь попадет раньше (или позже); в каких из них процесс будет останавливаться чаще, а в каких — реже? Оказывается, ответ на эти вопросы легко получить, если снова воспользоваться фундаментальной матрицей.
Обозначим через b ij вероятность того, что процесс завершится в некотором поглощающем состоянии S j при условии, что начальным было состояние S i . Множество состояний b ij снова снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы — всем всем поглощающим состояниям. В теории ДМЦ доказывается, что матрица В определяется следующим образом:
М — фундаментальная матрица с размерностью S;
R — блок фундаментальной матрицы с размерностью r.
Рассмотрим конкретный пример системы с четырьмя состояниями S 1 — S 4 , две из которых — S 1 , S 2 — поглощающие, а две — невозвратные: S 3 и S 4 (рис.8.10):
S 1 S 2 S 3 S 4
Рис. 8.10. Система с четырьмя состояниями
Для наглядности и простоты вычислений обозначим переходные вероятности следующим образом:
P 11 = P 22 = 1; P 31 = P 43 = q ; P 34 = P 42 = P.
Остальные значения вероятностей будут нулевыми. Каноническая форма матрицы перехода в этом случае будет выглядеть так:
Фундаментальная матрица после вычислений примет вид:
Тогда, согласно формуле (8.9), матрица вероятностей поглощения вычисляется так:
Поясним вероятностный смысл полученной матрицы с помощью конкретных чисел. Пусть p = 0,7 , а q = 0,3. Тогда, после подстановки полученных значений в матрицу В, получим:
Таким образом, если процесс начался в S 3 , то вероятность попадания его в S 1 равна 0,38 , а в S 2 — 0,62. Отметим одно интересное обстоятельство: несмотря на то, что , казалось бы, левое поглощающее состояние («левая яма») находится рядом с S 3 , но вероятность попадания в нее почти в два раза меньше, чем в «удаленную яму» — S 2 . Этот интересный факт подмечен в теории ДМЦ и объясняется он тем, что p > q , то есть процесс имеет как бы «правый уклон». Рассмотренная выше модель называется в теории ДМЦ моделью случайного блуждания. Такими моделями часто объясняются многие физические и технические явления и даже поведение игроков во время различных игр.
В частности, в рассмотренном примере объясняется факт того, что более сильный игрок может дать заранее значительное преимущество («фору») слабому противнику и все равно его шансы на выигрыш будут более предпочтительными.
Кроме указанных выше средних характеристик вероятностного процесса с помощью фундаментальной матрицы можно вычислить моменты и более высоких порядков. В частности, дисперсия числа пребывания в том или ином состоянии — D определяется с помощью следующей матрицы:
М dg — диагональная матрица, т.е. матрица, полученная из М путем оставления в ней лишь диагональных элементов и замены остальных элементов нулями. Например, приведенная выше матрица (8.7а) будет иметь вид:
В свою очередь, матрица М представляет собой матрицу, полученную из М путем возведения в квадрат каждого ее элемента, то есть для (8.7а) будем иметь:
Аналогичным образом определяема и дисперсия для общего количества раз пребывания в том или ином состоянии М е , Обозначим ее D е .
8.2.2. Эргодические цепи
Как указывалось выше под эргодической ДМЦ понимается цепь, не имеющая невозвратных состояний. Таким образом, в такой цепи возможны любые переходы между состояниями. Напомним, что эргодические цепи могут быть регулярными и циклическими. Определение таких цепей было дано выше.
Поскольку согласно данному выше определению в эргодической ДМЦ на любом шаге должны быть возможными любые переходы, то очевидно при этом, что переходные вероятности не должны равняться нулю. Оказывается, из этого условия вытекают некоторые замечательные свойства регулярных ДМЦ:
. Степени П [n] k при к (r) 0 стремятся к стохастической матрице A [n] ;
. Каждая строка матрицы А [n] представляет один и тот же вероятностный вектор
a = а 1 , а 2 . а n > , (8.12)
все компоненты которого положительны.
Вектор (8.12) в теории ДМЦ занимает особое место из-за наличия многих приложений и называется вектором предельных или финальных вероятностей (иногда — стационарным вектором). Финальные вероятности определяют с помощью векторно-матричного уравнения
которое в развернутом виде будет выглядеть так:
К уравнениям (8.13а) можно дополнительно добавить условие нормировки:
Тогда любое из уравнений в (8.14) можно исключить.
Также как и в случае поглощения ДМЦ многие характеристики эргодических цепей определяются с помощью фундаментальной матрицы , которая в этом случае будет иметь вид:
Для эргодических цепей характеристикой, имеющей важное практическое значение, является продолжительность времени, за которое процесс из состояния S i впервые попадает в S j , так называемое время первого достижения . Матрица средних времен достижения определяется по формуле:
M z — фундаментальная матрица (8.15);
M zdg — диагональная матрица, образованная из фундаментальной, заменой всех элементов, кроме диагональных — нулями;
D — диагональная матрица с диагональными элементами d ii = 1/ a i ;
Е — матрица, все элементы которой равны единице.
Матрица дисперсий времени первого достижения имеет несколько более сложный вид:
где кроме уже упомянутых обозначений встречается новое — (М z Ч М t ) dg , обозначающее диагональную матрицу, полученную из матричного прозведения матриц М z Ч М t .
8.2.3. Управляемые марковские цепи
Как указывалось выше, под управляемыми марковскими процессами понимают такие, у которых имеется возможность до определенной степени управлять значениями переходных вероятностей. В качестве примеров таких процессов можно привести любые торговые операции, у которых вероятность сбыта и получения эффекта может зависеть от рекламы, мероприятий по улучшению качества, выбора покупателя или рынка сбыта и т.д.
В лесной отрасли эффективность может зависеть, например, от региональной лесомелиорации, оптимальной стратегии лесопользования (рубки ухода, технологические приемы, комплекс машин, дорожная сеть и т.д.) Ниже будут приведены конкретные примеры, здесь же мы остановимся на особенностях применяемого математического аппарата.
Очевидно, что при создании математических моделей в данном случае должны фигурировать следующие компоненты:
конечное множество решений (альтернатив) K i ,
где i О S — номер состояния системы;
матрицы переходов П [s] (k) , соответствующие тому или иному принятому к-решению;
матрицы доходов (расходов) R [s] (k) , также отражающие эффективность данного решения.
Управляемой цепью Маркова (УЦМ) называется случайный процесс, обладающий марковским свойством и включающий в качестве элементов математической модели конструкцию (кортеж) K i , П [s] (k) , R [s] (k) > . Решение, принимаемое в каждый конкретный момент (шаг процесса) назовем частным управлением .
Таким образом, процесс функционирования системы описываемой УЦМ, выглядит следующим образом:
если система находится в состоянии i О S и принимается решение k О K i то она получает доход r i (k) ;
состояние системы в последующий момент времени (шаг) определяется вероятностью P ij (k) , то есть вероятность того, что система из состояния i О S перейдет в состояние j О S , если выбрано решение K i .
Очевидно, общий доход за n-шагов является случайной величиной, зависящей от начального состояния и качества принимаемых в течение хода процесса решений, причем это качество оценивается величиной среднего суммарного дохода (при конечном времени) или среднего дохода за единицу времени (при бесконечном времени).
Стратегией p называется последовательность решений:
p = ( f 1 , f 2 , . f n ) , (8.22)
f n = k 1 , k 2 , . k n > О k — вектор управления.
Задание стратегии означает полное описание конкретных решений, принимаемых на всех шагах процесса в зависимости от состояния, в котором находится в этот момент процесс.
Если в последовательности (вектора) p все f одинаковы, то такая стратегия называется стационарной , т.е. не зависящей от номера шага. Стратегия p = ( f 1 , f 2 , . f n ) называется марковской , если решение f n принимаемое в каждом конкретном состоянии зависит только от момента времени n, но не зависит от предшествующих состояний.
Оптимальной будет такая стратегия, которая максимизирует полный ожидаемый доход для всех i и n. В теории УМЦ разработаны два метода определения оптимальных стратегий: рекуррентный и итерационный [].
Первый, рекуррентный метод, применяется чаще всего при сравнительно небольшом числе шагов n. Его идея основана на применении принципа Беллмана и заключается в последовательной оптимизации дохода на каждом шаге с использованием рекурентного уравнения следующего вида:
— полный ожидаемый доход;
шагов, если система находится в состоянии i;
— непосредственно ожидаемый доход, т.е. доход на одном шаге, если процесс начался с i состояния;
— величина полного ожидаемого дохода за n- прошедших шагов, если процесс начинался с j-того состояния (i № j).
Таким образом, данный метод, по существу, аналогичен методу динамического программирования, отличием является лишь то, что на каждом шаге учитывается вероятность попадания системы в то или иное состояние. Поэтому этот метод называют стохастическим динамическим программированием.
Конкретное применение метода будет рассмотрено ниже на примере.
Второй — итерационный метод оптимизации применяется при неограниченном числе этапов (шагов) процесса. Этот метод использует свойство эргодичности марковской цепи и заключается в последовательном уточнении решения путем повторных расчетов (итераций). При этих уточнениях находят решение, обеспечивающее в среднем минимум дохода при большом числе шагов. Оно уже не будет зависеть от того, на каком шаге производится оценка оптимальной стратегии, то есть является справедливым для всего процесса, независимо от номера шага. Важным достоинством метода является, кроме того, и то, что он дает возможность определить момент прекращения дальнейших уточнений.
Главным отличием итерационного метода от рассмотренного выше, рекурентного, заключается в том, что в данном случае используется матрица предельных (финальных) вероятностей, где вследствие свойства эргодичности переходные вероятности постоянны на всех шагах процесса. Поскольку матрица доходов состоит также из постоянных, не зависимых от n величин, то можно предположить, что с ростом n общая величина доходов будет возрастать линейно.
Представим графически линейную зависимость суммарного дохода от числа шагов u i (n) (рис. 8.11)
Рис.8.11. Зависимость суммарного дохода от числа шагов
Для наглядности график (рис. 8.11) изображен для УМЦ с двумя состояниями S 1 и S 2 . На графике прямая V 1 (n) показывает зависимость суммарного дохода, если система «стартовала» из состояния S 1 . Соответственно, прямая V 2 (n) изображает ту же зависимость для состояния S 2 . Обе прямые могут быть описаны линейными уравнениями V i (n):
g — угловой коэффициент прямой V i (n);
V i (0) — доход в i-том состоянии в конце процесса.
Легко заметить, что при таком представлении зависимости V i (n) величина непосредственно ожидаемого дохода q (см. формулу (8.23)) заменяется g. Отличие здесь лишь в том, что g является величиной постоянной для всего процесса, в то время как q меняется на каждом шаге. Величина V i (n) показывает, на сколько в среднем отличается доход, когда процесс заканчивается в том или ином состоянии, В теории марковских цепей V i (n) называют весом , так как разница V i (0) — V 2 (0) при двух состояниях показывает средний выигрыш от того, в каком состоянии мы находимся в конце процесса (независимо от выбранной стратегии). Таким образом, подводя итоги общих рассуждений, можно сказать, что свойство эргодичности позволяет нам считать справедливым приближенное равенство:
На этом предположении и основан итерационный метод. Суть его сводится к тому, что при разных стратегиях путем последовательных приближений определяются значения сумм
Таким образом, если ранее (при рекурентном методе) искалась стратегия, обеспечивающая на каждом шаге максимум суммы непосредственно ожидаемого дохода и дохода на предшествующих шагах, то здесь находится стратегия, обеспечивающая максимум средней прибыли и относительного веса сразу для всего процесса. При этом производятся последовательные расчеты — итерации, на каждом этапе которых уточняются значения угловых коэффициентов и весов, обеспечивающие максимум доходов.
Конкретные примеры расчетов как по первому, так и по второму методам будут даны ниже.
8.3. Примеры принятия решений с помощью марковских цепей
Как указывалось выше, простота и наглядность математического аппарата ДМЦ позволяет эффективно использовать его для принятия решений. При этом можно выделить два подхода:
статический (одношаговый), когда на основании матема-тической модели, описывающей поведение системы в какой-либо момент времени на одном шаге, получают функциональные зависимости показателя эффективности от управляемых переменных (целевую функцию). Далее путем обычных процедур программирования получают оптимальные значения управляемых переменных, обеспечивающих получение максимального эффекта.
динамический (многошаговый), когда проигрывается поведение системы на протяжении планируемого периода и определяется оптимальная стратегия (стохастическое динамическое программирование).
Рассмотрим сначала примеры первого типа.
Пример 8.1. Лесопосадки.
Допустим, что требуется оценить эффективность лесопосадочной операции и принять решение по ее повышению. В данном случае система включает лесопосадочную машину (ЛПМ) и набор саженцев (С), которые необходимовысадить на делянке с учетом требований технологии. В каждом шаге операции примем одну рабочую смену — 6 час.
Предположим, что начало работы машины и подготовки саженцев происходит с одной и той же вероятностью p (причем отказ равен q=1-p ). Очевидно, что после успешного начала работы ЛПМ могут произойти следующие случайные события:
В 1 — посадка всех саженцев произошла успешно и ЛПМ в конце работы исправна (цель операции достигнута);
В 2 — во время работы ЛПМ произошел отказ, который может быть устранен на месте (обычно время восстановления лимитируется 30 мин.);
В 3 — во время работы машины произошел неустранимый отказ и она должна быть заменена;
В 4 — при исправной работе машины из-за нарушения технологии посадка саженцев произведена некачественно и требуется пересев;
В 5 — из-за неисправной работы машины посадка произведена некачественно.
Вероятность указанных условных событий (при условии успешного начала — p) обозначим:
а поскольку они несовместны и образуют полную группу, то
В результате реализации событий В i [i=1,2. 5] используемый процесс в любой момент времени может находиться в одном из следующих состояний (рис.8.12)
Рис. 8.12. Состояния системы
А 1 — посадка произведена успешно и в конце дня ЛПМ исправна;
А 2 — вследствие устранения отказа посадка произведена не пол-ностью. Исходя из допустимого времени устранения, можно полагать, что план не выполнен примерно на 15-20 % ;
А 3 — план не выполнен, требуется замена машины;
А 4 — план не выполнен, требуется новый комплект саженцев, ма-шина исправна;
А 5 — требуется новый комплект саженцев и исправная машина.
Последнее состояние, по существу, является начальным . Если предположить, что состояние системы в начале каждого рабочего дня связано только с результатом предыдущего и вероятностным образом связано с ним то можно считать, что рассматриваемая операция представляет собой простую дискретную марковскую цепь. Кроме того, предположим, что переходные вероятности такой цепи не зависят от номера испытания (шага), то есть цепь является однородной . Из анализа состояний видно, что в состоянии А 1 процесс останавливается (цель операции достигнута), т.е. оно является поглощающим.
Таким образом, согласно принятым допущениям модель рассматриваемой операции представляет собой простую однородную поглощающую дискретную марковскую цепь с пятью состояниями. Переходные вероятности такой цепи определим с помощью алгебры событий:
Соответственно, матрица перехода будет иметь вид:
А 1 А 2 А 3 А 4 А 5
В соответствии с приведенным выше математическим аппаратом матрица (8.29) может быть представлена в каноническом виде:
где, в данном случае,
— одноэлементная единичная под-матрица;
— вектор-столбец, описывающий переходы из невозвратных в эргодические состояния.
Подматрица Q, описывающая процесс переходов в системе до выхода из невозвратного множества состояний выделена двойным пунктиром в матрице (8.29).
Как было сказано выше, после представления переходной матрицы в каноническом виде (8.29а), можно определить ряд характеристик, с помощью которых составляется целевая функция и принимается решение. В качестве критериев в данном случае могут фигурировать:
1. вероятность успешного проведения операции при заданном расходе средств на ее проведение Р(С 2 ) — (прямая задача);
2. необходимое (гарантированное) количество средств, обеспечивающее проведение работы с заданной вероятностью;
3. математические ожидания и дисперсии случайных расходов средств на операцию.
Рассмотрим в качестве критериев средние значения количеств ремонтов (или замен) ЛПХ — m z1 и комплектов саженцев m z2 . Кроме того, в расходы войдут: стоимость частичного ремонта ЛПХ, а также расходы, связанные с дополнительным высевом саженцев при попадании в состояние А 2 .
Таким образом, если задать величины расходов, связанные с попаданием в то или иное состояние (А 2 , А 3 , А 4 , А 5 ) и опре-делить среднее число раз попадания в эти состояния, то в целом будут определены расходы на операцию.
Представим таблицу (или матрицу) расходов в виде:
Состояния
Расходы
С чр + 0,2С с
С тр + С с
С чр , С тр — соответственно, стоимость частичного или полного ремонта трактора;
С с — стоимость комплекта саженцев и их посадки.
Среднее количество раз попадания в то или иное состояние (до поглощения) определится, как указывалось с помощью фундаментальной матрицы (стр. ). При этом надо иметь в виду, что, поскольку в данном случае процесс начинается только с состояния А 5 , то вычислять надо не все элементы матрицы (8.7), а лишь члены последней строки, т.е. m 41 , m 42 , m 43 и m 44 .
В буквенном выражении все элементы матрицы (8.7) представляют довольно сложные выражения, поэтому далее приведем конкретный числовой пример:
Пусть значения r i будут равны: r 1 = 0,77; r 2 = 0,1; r 3 = 0,05; r 4 = 0,04; r 5 = 0,03; р = 0,8.
Тогда после вычислений матрица (8.7) будет иметь вид:
Тогда среднее число замен посадочного материала и трактора будет равно, соответственно:
m с = m 42 + m 44 = 1,296;
m тр = m 43 + m 44 = 1,375;
а с учетом стоимости комплекта саженцев и материала:
С е = 1,296 С с + 1,375С тр (8.31)
Полученное выражение (8.31) позволяет решить три задачи:
1. Определить, соответствуют ли расходы на операцию располагаемым;
2. Произвести выбор оптимальных значений r i , обеспечивающих min С е ;
3. Оценить степень влияния каждой вероятности r i на эффек-тивность операции и наметить мероприятия по ее провышению.
Пример 8.2. Сукцессионные изменения на верховом болоте (эргодическая ДМЦ).
В работе Дж.Джефферса [ ] эргодическая ДМЦ фигурирует в виде модели сукцессионных изменений на верховом болоте. При этом принимается временный интервал (шаг), равный 20 годам.
В качестве состояний системы принимаются:
S 1 — болото; S 2 — Calluna ( вереск); S 3 — лес; S 4 — мелкий подрост, выеденный крупными травоядными.
Матрица перехода с учетом принятых в цитируемой работе переходных вероятностей P ij в начальный момент имеет вид:
S 1 S 2 S 3 S 4
Несмотря на наличие нулей в первоначальной матрице, в работе показано, что в данной цепи отсутствуют поглощающие состояния и через некоторое количество шагов в ней возможны любые переходы и оно является эргодической. Так, например, с помощью уравнения Колмогорова-Чепмена (8.4) показано, что уже через два шага матрица имеет вид:
При последовательном возведении в более высокие степени, как указывалось выше, матрица эргодической цепи будет иметь одинаковые строки, то есть «стягивается» в вектор финальных вероятностей. В данном случае этот вектор имеет вид:
Таким образом, если вероятности переходов оценены правильно и остаются постоянными в течение длительного времени, данная экосистема достигает равновесного состояния, в котором примерно 22 % площади будет занято болотом и, соответственно, по 25, 38 и 15 % занимают Calluna, лес и участок подроста.
На основании формулы (8.20) вычисляются средние времена первых достижений каких-либо состояний. При этом матрица M t будет иметь вид:
Таким образом, на основании данной матрицы можно определить, например, что среднее время, необходимое для того, чтобы участок, где преобладает Calluna, превратился в болото, составляет 9,566 Ч 30 = 191 год. Аналогично, лес превратится в участок с Calluna через 4,107 Ч 20 = 82 года. Наконец, зная матрицу времен и вектор финальных вероятностей, можно определить вектор средних времен первых достижений в равновесном состоянии экосистемы:
Поскольку каждый временной шаг принимался 20 годам, то среднее время, чтобы случайно выбранный участок превратился, например, в болото, будет равно 10,385 * 20 = 208 лет.
Таким образом, на основании данной математической модели можно прогнозировать тенденции развития той или иной экосистемы и принимать какие-либо решения. Следует лишь сделать оговорку, что, во-первых, данный прогноз будет сильно зависеть от точности исходных данных и, во-вторых, при этом не учитывается влияние антропогенных и других внешних воздействий.
Пример 8.3. Эргодическая ДМЦ
В приведенном выше примере финальная вероятность эргодической цепи определялись с помощью уравнения Колмогорова-Чепмена, однако, как указывалось выше, эти вероятности могут определяться и иным путем, с помощью решения системы уравнений вида (8.14). Такая задача возникает, в частности, при определении оптимальной стратегии контроля.
Как известно, существует два принципиально разных метода контроля: сплошной и выборочный.
Как показывают сами названия, при сплошном контроле проверяются подряд все образцы продукции. При этом методе, конечно, есть полная уверенность в отсутствии брака, однако, велики материальные затраты. При выборочном контроле существует вероятность пропуска бракованной продукции, но резко снижаются расходы, связанные с проверкой. Очевидно, при этом возникает задача определения оптимальной стратегии контроля. Одним из вариантов, в частности, может быть переменный контроль, когда при нормальном ходе производства контролируются малые выборки образцов продукции, а при повышении числа дефектных изделий контоль усиливается за счет больших размеров выборок. После проведения каких-либо мероприятий, направленных на устранение причин брака, можно вернуться к прежнему методу контроля. При такой формулировке задачи, очевидно, мы имеем дело со случайной последовательностью событий, обладающей марковским свойством. В данном случае ДМЦ будет иметь всего два состояния: S 1 — контроль при большой выборке и S 2 — контроль при малой выборке.
Изобразим одну реализацию процесса графически (рис. 8.13):
Видео:Матрица интенсивностей. Система уравнений КолмогороваСкачать

Уравнения Колмогорова.
Предельные вероятности состояний
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .
Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:
Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.
1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:
2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .
Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).
Применяя теорему сложения вероятностей, получим
Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)
Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:
Решив систему, получим .
Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:
Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Видео:уравнение колмагороваСкачать

Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния
для состояния имеем , которое с учетом (12) приводится к виду
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
к которой добавляется нормировочное условие
При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.
Решая систему (14), (15), можно получить
Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .
Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
🎬 Видео
Предельные вероятности состоянийСкачать

Цепи Маркова (видео 12) | Теория информации | ПрограммированиеСкачать

Случайные процессы 9. Марковские процессы.Скачать

Цепи МарковаСкачать

Цепи МарковаСкачать

Чиркин А. С. - Математические модели флуктуационных явлений - Марковский процессСкачать

Марковские процессы [1] // Александр БуфетовСкачать
![Марковские процессы [1] // Александр Буфетов](https://i.ytimg.com/vi/OmTz7EEs--4/0.jpg)
Соколов Д. Д. - Теория случайный процессов - Марковские цепи с непрерывным набором состоянийСкачать

Соколов Д. Д. - Теория случайный процессов - Марковские процессы с непрерывным временемСкачать

Сердобольская М. Л. - Теория случайных процессов - Марковские случайные процессы (Лекция 4)Скачать

04 Эргодические цепи МарковаСкачать

Случайные процессы 8 Марковские цепиСкачать

Лекция 13. Непрерывные марковские процессы. 30.04.2021Скачать

ЦОС Python #4: Марковские процессы в дискретном времениСкачать

Марковские процессы [2] // Александр БуфетовСкачать
![Марковские процессы [2] // Александр Буфетов](https://i.ytimg.com/vi/HyqSiO2kI5E/0.jpg)
Шкляев А. В. - Теория случайных процессов. Семинары - Лекция 7Скачать

Лекция 12. Непрерывные цепи Маркова (продолжение). 23.04.2021Скачать