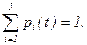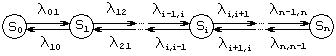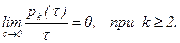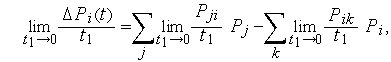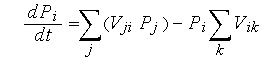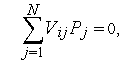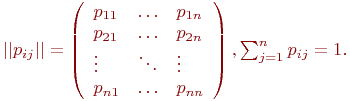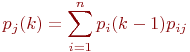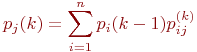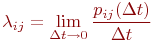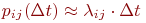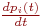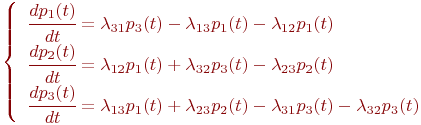Уравнения Колмогорова
На практике значительно чаще встречаются ситуации, когда переходы системы из состояния в состояние происходит в случайные моменты времени, которые заранее указать невозможно: например, выход из строя любого элемента аппаратуры, окончание ремонта (восстановление) этого элемента. Для описания таких процессов в ряде случаев может быть с успехом применена схема марковского случайного процесса с дискретными состояниями и непрерывным временем – непрерывная цепь Маркова. Покажем, как выражаются вероятности состояний для такого процесса. Пусть S=. Обозначим через pi(t) — вероятность того, что в момент t система S будет находиться в состоянии 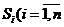
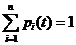
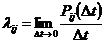
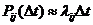
Если 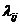
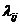
 |
Интегрирование этих уравнений при известном начальном состоянии системы даст искомые вероятности состояний как функции времени. Заметим, чтоp1+p2+p3+p4=1 и можно обойтись тремя уравнениями.
Переход из одного состояния в другое может быть отображен графом состояний, в котором вершины представляют собой возможные состояния системы, а дуги графа отражают переходы из одного состояния в другое. Если две вершины i и j соединяются дугой (i,j), то это означает, что возможен непосредственный переход из состояния i в состояние j. Марковская цепь может, таким образом, быть представлена как случайное блуждание на графе состояний системы.
Поскольку переход из одного состояния в другое для СМО возможен в любой момент времени, определяемый появлением заявки во входном потоке, то для изучения СМО применяются непрерывные марковские цепи.
Одна из важнейших задач теории марковских процессов вообще и ТМО в частности заключается в нахождении вероятностей состояний цепи. Эти вероятности для непрерывных марковских цепей определяются с помощью дифференциальных уравнений Колмогорова.
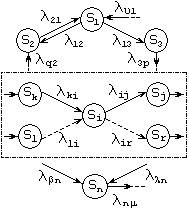
Рассмотрим некоторую произвольную систему, граф состояний которой приведен на рис.1. Система имеет n состояний S1,S2. Sn. Процесс перехода из одного состояния в другое описывается непрерывной цепью Маркова. Пусть Pi(t) — вероятность того, что в момент времени t система будет находиться в состоянии Si (i=1,2,…,n). Поскольку система не может находиться одновременно в двух состояниях, то события, заключающиеся в нахождении системы в состояниях S1,S2,…,Sn, несовместны и образуют полную систему событий. Отсюда следует
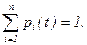
Это соотношение называется условием нормировки. Задача заключается в определении вероятности любого состояния Pi(t) в любой момент времени t.
Введем понятие вероятности перехода системы из состояния i, где она находилась в момент времени t, в состояние j за время Dt Pij(t,Dt). Очевидно, что Pij(t,Dt) представляет собой условную вероятность того, что в момент времени t + Dt система окажется в состоянии Sj при условии, что в момент времени t она находилась в состоянии Si: pij(t,Dt)= p(Sj(t+Dt)/Si(t)).
Предел отношения вероятности перехода pij(t,Dt) к длине интервала времени Dt назовем плотностью вероятности перехода
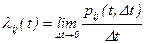
Плотность вероятности перехода определим только для случаев i¹j.
Если lij(t)=const, то марковская цепь называется однородной. В противном случае, когда lij(t) являются функциями времени, цепь называется неоднородной. При расчетах вероятностей состояний марковской цепи предполагается, что все эти плотности вероятностей переходов lij известны. Если у каждой дуги графа состояний системы проставить плотность вероятности перехода по данной дуге, то полученный граф назовем размеченным графом состояний (см.рис.1). Уравнения Колмогорова составляются в соответствии с размеченным графом состояний. Рассмотрим фрагмент размеченного графа состояний (рис.1), обведенный штрихпунктирной линией. Отбросим вначале дуги, изображенные пунктиром, и определим вероятность нахождения системы в состоянии Si в момент времени t+Dt. С учетом того, что вершина Siсвязана только с вершинами Sk и Sj, указанное событие будет иметь место в двух случаях:
— система находилась в состоянии Si в момент времени t и за время Dt из этого состояния не вышла;
— система находилась в состояния sk в момент времени t и за время Dt перешла из Skв Si.
Если отрезок Dt достаточно мал, то вероятность перехода pij(t,Dt) может быть определена приближенно с помощью (52)
С учетом (53) и свойства марковости процесса вероятность первого случая (отсутствие перехода по дуге (Si,Sj))
Вероятность второго случая с учетом (53)
Тогда можно определить искомую вероятность как
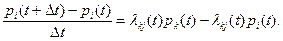
Переходя в (53) к пределу при Dt ® 0, получим
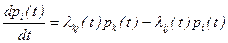
Теперь добавим к вершине Si дуги, обозначенные на рис.1 пунктиром. Тогда при вычислении pi(t+Dt) необходимо учитывать возможный переход из Si в Sj и Sr и переходы из Sk и Sl в Si. В этом случае
Повторяя вышеописанные рассуждения, получим
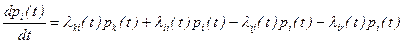
На основании (55) и (56) можно сформулировать правила составления уравнений Колмогорова по размеченному графу состояний непрерывной марковской цепи:
1. Система дифференциальных уравнений Колмогорова имеет форму Коши. Каждое уравнение составляется с помощью рассмотрения вероятности состояния, представленного соответствующей вершиной в размеченном графе. Число уравнений системы равно числу вершин графа.
2. Число слагаемых правой части каждого уравнения равно числу дуг, инцидентных соответствующей вершине.
3. Дугам с положительной инциденцией соответствуют отрицательные слагаемые, а дугам с отрицательной инциденцией — положительные.
4. Каждое слагаемое правой части равно произведению вероятности состояния, соответствующего началу рассматриваемой дуги, на плотность вероятности перехода по данной дуге.
Начальные условия для системы уравнений Колмогорова определяются начальным состоянием системы. Например, если начальное состояние было S2 , то начальные условия имеют вид: p1(0)=0; р2(0)=1; р3(0)=0;…;рn(0)=0. Уравнения (55) и (56) были выведены для общего случая неоднородной марковской цепи. Для однородной марковской цепи все lij(i,j=l,…,n) постоянны.
Рассмотрим одно важное свойство уравнений Колмогорова (55), которое может быть представлено в виде
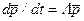
где 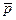
В соответствии с вышеописанными правилами составления уравнений Колмогорова одна и та же плотность вероятности перехода lij будет входить в одно из уравнений со знаком «+», а в другое — со знаком «-«, поскольку для двух смежных вершин дуга, соединяющая их, будет обладать положительной инциденцией по отношению к одной вершине и отрицательной по отношению к другой. Это приведет к тому, что сумма всех элементов в каждом столбце матрицы будет равна нулю. Тогда любая строка матрицы L будет равна сумме остальных строк. Следовательно, матрица L является всегда вырожденной. Более строго это свойство доказывается в [7].
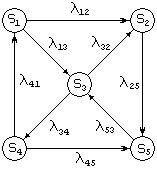
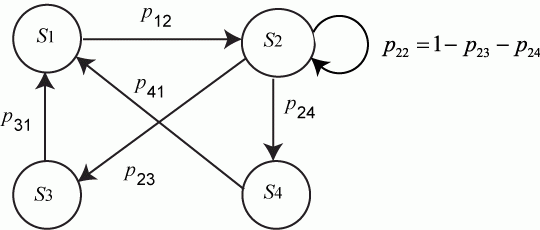
Рассмотрим систему с размеченным графом состояний, изображенным на рис.2. Система уравнений Колмогорова и матрица L для этого случая в соответствии с правилами 1-4 будут иметь вид:
Исключение любого уравнения из этой системы нарушает указанное соотношение для строк матрицы L, следовательно, ранг матрицы L будет равен n-1. Для того чтобы система уравнений Колмогорова имела единственное решение при заданных начальных условиях, необходимо исключить любое из уравнений системы (58) и заменить его условием нормировки (51).
Итак, решение системы (57) без одного уравнения (безразлично какого) с условием (51) определяет в любой момент времени поведение вероятностей состояний марковской цепи при заданных начальных условиях.
Получить это решение можно с помощью любых численных методов (например, Рунге-Кутта, Эйлера-Коши и т.д.), реализуемых на ЭВМ. Только в самых простых случаях система уравнений Колмогорова может быть проинтегрирована в квадратурах. В большинстве практических случаев для расчета вероятностей состояний используются не решения систем уравнений Колмогорова в любой момент времени, а асимптотические оценки этих решений при t®¥.
Лекция 15. Предельные вероятности состояний. Простейший поток событий.
Асимптотические оценки в соответствии с известной теоремой А.А.Маркова могут быть получены для марковских цепей, обладающих эргодическим свойством.
Определение 1. Если число состояний системы конечно и из каждого состояния можно перейти в любое другое за произвольное число шагов, то говорят, что такая система обладает эргодическим свойством.
Определение 2. Пусть марковский процесс характеризуется вероятностями перехода из состояния i в состояние j за время t
Процесс называется транзитивным, если существует такое t>0, что pij(t)>0 (0£i£n; 0£j£n). Из определений 1 и 2 следует, что процессы в марковских цепях с эргодическим свойством являются транзитивными.
Теорема Маркова. Для любого транзитивного марковского процесса предел 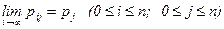
Это означает, что при t®¥ в системе устанавливается некоторый предельный стационарный режим, характеризующийся постоянной, не зависящей от времени, вероятностью каждого из состояний системы. При этом данная вероятность представляет собой среднее относительное время пребывания системы в данном состоянии. Это значит, что если время работы всей системы 100 ч, а вероятность состояния S1 равна p1=0,15, то система будет находиться в состоянии S1 в среднем 15 ч.
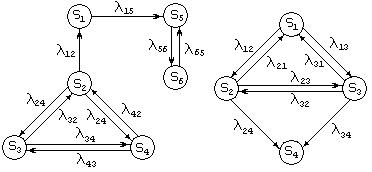
Пределы, к которым стремятся вероятности каждого из состояний марковской цепи с эргодическим свойством при t®¥, называются предельными вероятностями. При рассмотрении СМО мы будем иметь дело только с эргодическими марковскими цепями. Пусть V — некоторое подмножество множества состояний системы S , а V’ — его дополнение до S . Если множество V обладает эргодическим свойством и ни из одного состояния множества V нельзя перейти ни в одно из состояний множества V’, то множество называется замкнутым или эргодическим множеством. Эргодические системы состоят из одного единственного эргодического множества (S=V, V’=Æ) и называются поэтому неразложимыми. Если в системе S множество V’¹Æ или в этой системе можно выделить несколько эргодических множеств S = V1ÈV2È…ÈVn, то такая система называется разложимой. Примеры таких систем приведены на рис.3.
На рис.3,а представлена система с двумя эргодическими множествами V1=(S2,S3,S4) и V2(S5,S6). На рис.3, б эргодическое множество состоит лишь из одного состояния (S4). Если эргодическое множество состоит лишь из одного состояния, то это состояние называется поглощающим, так как попав в него однажды, процесс остается навсегда в поглощающем состоянии. Характерная особенность графа состояний неразложимой эргодической марковской системы заключается в том, что каждой вершине этого графа инцидентны дуги как с положительной, так и с отрицательной инцидентностью (т.е. у каждой вершины имеются дуги, направленные как к вершине, так и от нее, см., например, рис. 1 и 2).
Вычисление предельных вероятностей состояний для таких систем упрощается в связи с тем, что, поскольку все эти вероятности являются постоянными величинами, то их производные по времени равны 0 (dpi/dt=0 для всех i). Поэтому левые части системы уравнений Колмогорова (58) приравниваются нулю и она превращается в систему линейных алгебраических уравнений
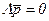
Нетривиальное решение системы (59) может быть получено только в случае вырожденности матрицы L. Выше было доказано, что матрица плотностей вероятностей L является вырожденной. Система (59) без одного из своих уравнений дополняется условием нормировки

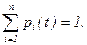
Соотношения (59) и (60) позволяют определить предельные вероятности состояний. Поскольку часть слагаемых, соответствующая дугам с отрицательной инцидентностью, положительна, а другая часть, соответствующая дугам с положительной инцидентностью, отрицательна, то каждое уравнение системы (59) может быть составлено с учетом мнемонического правила: для каждого состояния сумма членов, соответствующих входящим дугам, равна сумме членов, соответствующих выходящим дугам.
Пример. Для системы, изображенной на рис.2, из уравнений Колмогорова (58) следует
Для решения (61) нужно исключить любое из первых пяти уравнений (например, пятое, как содержащее наибольшее число членов).
Предельные вероятности состояний используются в ТМО значительно чаще, чем решения уравнений Колмогорова, причем, зная решение системы уравнений Колмогорова, можно определить момент окончания переходного процесса изменения вероятностей состояний во времени. Это дает возможность рассчитать, промежуток времени начиная от включения системы в работу, по истечении которого вероятности состояний достигнут своих предельных значений и будут справедливы оценки, использующие эти значения. В заключение этого параграфа рассмотрим один частный, но практически очень важный класс марковских процессов, широко применяемых при исследовании СМО. Это — процессы «размножения и гибели». К ним относятся марковские цепи, представимые размеченным графом, который состоит из вытянутой цепочки состояний, изображенной на рис.4.
Матрица плотностей вероятностей переходов такой системы является якобиевой (тридиагональной):
Рассматривая начальное состояние S0 , получим в соответствии с (59)
Для состояния S1 имеем
Вычитая из (63) равенство (62), получим
Продолжая этот процесс до n-гo состояния включительно, получим
Из (62) теперь можно выразить p1 через р0:
Подставляя (64) в (65), получим
Очевидно, что для произвольного k (1£k£n) будет справедливо выражение
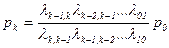
В соответствии с (66) и размеченным графом состояний, представленным на рис.4, можно сформулировать правило, с помощью которого можно выразить предельные вероятности состояний процесса «размножения и гибели» через вероятность начального состояния р0. Это правило гласит: вероятность произвольного состояния pk (l£k£n) равна вероятности начального состояния р0, умноженной на дробь, числитель которой равен произведению плотностей вероятностей перехода для дуг, переводящих состояние системы слева направо, а знаменатель — произведение плотностей вероятностей перехода справа налево от начального до k-гo состояний включительно.
Вероятность р0 находится из условия нормировки 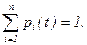
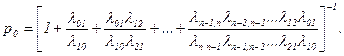
Выражения (66) и (67) полностью определяют предельные вероятности процесса «размножения и гибели».
Цепи Маркова с непрерывным временем являются математическими моделями СМО. Для анализа СМО необходимо также иметь математические модели входных потоков заявок на обслуживание. Эти математические модели представляют собой потоки события, являющиеся отдельным классом случайных процессов. Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени. Этот поток количественно может быть охарактеризован числом событий x(t), имевших место в течение определенного промежутка времени (0,t). Тогда случайный поток событий можно определить как случайный процесс x(t) (t³0), в котором функция x(t) является неубывающей функцией времени, способной принимать лишь целые неотрицательные значения. Иными словами, график функции x(t) является ступенчатой кривой с постоянной высотой ступеньки, равной единице, причем ширина ступеньки — случайная величина. Примерами таких потоков могут служить: поток вызовов на АТС, поток запросов в вычислительный центр коллективного пользования и т.п. Моменты появления событий можно отобразить точками на временной оси, поэтому поток событий часто представляется и как последовательность таких точек. Поток событий называется регулярным, если события следуют одно за другим через одинаковые, строго фиксированные промежутки времени.
В ТМО такие потоки практически, не используются, однако они представляют интерес как предельный случай. Значительно чаще имеют дело с потоками, в которых времена поступления событий и, следовательно, промежутки времени между ними являются случайными (иррегулярными). При этом наиболее простые расчетные соотношения получаются при использовании простейших потоков событий, которые широко применяются при исследовании CMО.
Простейшими называются потоки, обладающие следующими тремя свойствами: стационарностью, ординарностью и отсутствием последействия. Рассмотрим эти свойства подробнее.
1. Поток событий называется стационарным, если вероятность pk(l) того, что за отрезок времени t произойдет k событий, зависит только от его длины t и не зависит от его расположения на временной оси, т.е. pk(t’,t’+t)=pk(t). Из определения однородной марковской цепи следует, что стационарность — это однородность потока по времени.
2. Поток называется ординарным, если вероятность попадания на любой элементарный участок временной оси двух или более событий является бесконечно малой величиной, т.е.
3. Поток событий называется потоком без последействия, если вероятность попадания событий на некоторый участок временной оси не зависит от того, сколько событий попало на другие участки. Иными словами, условная вероятность наступления k событий за промежуток времени (t’,t’+t), вычисленная при любом условии чередования событий до момента t’, равна безусловной вероятности pk(t) того же события, т.е.
p[(t’,t’+t),k/(t»,t»+t),m]=pk(t),tÇtk=Æ, t» T), т.е. вероятность того, что случайная величина Т примет значение, меньшее чем t. Для этого необходимо определить вероятность того, что в интервал времени t, отсчитываемый от момента t0 появления некоторого события, попадет еще хотя бы одно событие (см.рис.5,б). Эту вероятность можно определить, зная вероятность отсутствия событий в интервале t, равную вероятности p0(t) состояния S0 на графе рис.5, а. В соответствии с (72)
F(t)=p(t>T)=1-e -lt , t>0 . (73)
Дифференцируя (73) по времени, получим искомый закон распределения
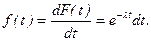
Закон распределения (74) называется показательным (экспоненциальным). Определим первые два момента показательного распределения:
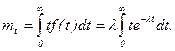
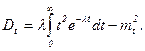
Интегрируя (75) и (76) по частям, получим
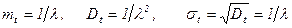
Из (77) следует, что для показательного распределения математическое ожидание и среднеквадратичное отклонение равны друг другу. Кроме того из (77) следует, что в простейшем потоке среднее время между двумя соседними событиями равно обратной величине интенсивности потока.
Определим теперь вероятность попадания одного события в простейшем потоке на элементарный участок временной оси (см.рис.5,б). Так же, как и в предыдущем случае, эта вероятность
Разлагая e -lDt в ряд по степеням lDt и ограничиваясь только первой степенью (в силу малости Dt), получим
Выражение в правой части (78) называется элементом вероятности появления события в простейшем потоке.
Марковские цепи являются математическими моделями некоторых реальных систем, а потоки событий являются моделями внешних воздействий на эти системы. В дальнейшем будем считать, что переход системы из одного состояния i в другое j в соответствии с размеченным графом состояний происходит под действием потока событий с интенсивностью lij, равной соответствующей плотности вероятности перехода. Эта интенсивность определяется как среднее число переходов из состояния i в состояние j за единицу времени.
Если все потоки событий являются пуассоновскими, то процесс в системе будет марковским.
Уравнения Колмогорова составляют основу аналитических моделей СМО. Их можно получить следующим образом.
Изменение вероятности 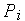
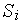
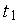
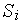
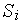
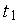
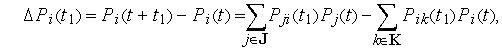
где 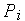
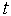
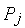
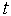
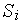
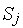
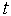
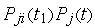
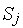
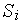
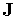
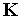
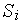
Разделив выражение (1) на 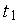
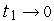
откуда следуют уравнения Колмогорова
В стационарном состоянии 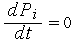
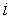
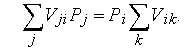
Прибавляя 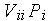
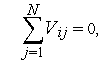
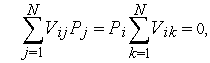
где 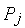
Условия существования стационарного режима:

— множество состояний системы должно быть эргодическим, т.е. из любого состояния Si можно за конечное число шагов перейти в состояниеSj .
Предельные вероятности состояний представляют собой среднее время пребывания системы в данном состоянии. Например, если у системы S три возможных состояния: S1, S2, S3 , причем их предельные вероятности равны 0.2, 0.3, 0.5, то это означает, что после перехода к установившемуся режиму система S в среднем две десятых времени будет находиться в состоянии S1, три десятых – в состоянии S2, половину времени – в S3.
Для вычисления предельных вероятностей необходимо в системе уравнений Колмогорова положить все левые части (производные) равными нулю. Действительно, в предельном (стационарном) режиме все вероятности состояний постоянны, а значит, их производные равны нулю. Следовательно, система дифференциальных уравнений превращается в систему линейных алгебраических уравнений.
Последнее изменение этой страницы: 2019-04-19; Просмотров: 467; Нарушение авторского права страницы
- Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний.
- Тема 5. Случайные процессы с дискретными состояниями и непрерывным временем. Статистическое моделирование экономических систем (метод Монте-Карло)
- Оглавление
- Вступление
- Непрерывные цепи Маркова
- Примеры
- Задание системы с конечным числом состояний и непрерывным временем наступления события (перехода из состояния в состояние)
- Определение плотности вероятностей перехода
- Потоки событий
- Свойства потока событий
- Стационарность
- Ординарность
- Отсутствие последействия
- Простейший поток
- Задача
- Модель 8. Гараж-непрерывный
- Уравнения Колмогорова
- Финальные вероятности состояний
- Пример. Составление ДУ Колмогорова
- Задание для самостоятельной работы.
- Как найти финальные вероятности системы?
- Процессы гибели и размножения
- Пример
- Пример
- Статистическое моделирование экономических систем (метод Монте-Карло)
- Теоретические основы метода
- Закон больших чисел
- Пояснение. Практический смысл.
- Предельная теорема о суперпозиции (наложении) потоков
- Пример.
- Примеры потоков, имеющих показательное (экспоненциальное) распределение:
- Схема решения задачи методом статистического моделирования
- Моделирование случайных величин
- 📸 Видео
Видео:Цепи Маркова с непрерывным временемСкачать

Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний.
Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова — старшего (1856 — 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
Марковские процессы делятся на два класса:
· дискретные марковские процессы (марковские цепи);
· непрерывные марковские процессы.
Дискретной марковской цепьюназывается случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.
Непрерывным марковским процессомназывается случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.
Система 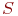
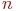
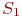
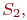
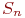
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 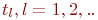
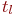
Известны вероятности перехода 

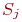
Цель моделирования: определить вероятности состояний системы после 
Обозначим эти вероятности 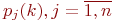

Если в системе отсутствует последействие, то есть вероятности 

Марковская цепь называется однородной, если переходные вероятности 
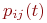
Значения 
Значения 
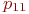
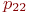
Не указываются также нулевые вероятности переходов. Например, на рис. это вероятности 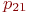
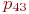
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
где 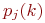
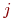

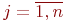
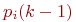
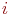

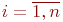
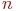

Рис.Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
где 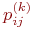

Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то — занятость. Если состояния объектов, то — поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости определить искомые вероятности.
В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей 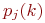
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 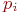

Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 
где 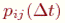


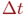
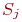
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов 

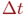
Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы 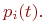
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
1. Определить состояния системы и плотности вероятностей переходов 
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части уравнения записывается производная вероятности 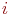
5. В правой части записывается алгебраическая сумма произведений 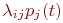
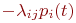
6. Определить начальные условия и решить систему дифференциальных уравнений.
Пример. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рисунке.
Рис. Размеченный граф состояний
Очевидно, 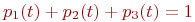
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера можно задать такие начальные условия: 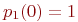
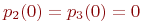
Дата добавления: 2015-04-03 ; просмотров: 7883 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Матрица интенсивностей. Система уравнений КолмогороваСкачать

Тема 5. Случайные процессы с дискретными состояниями и непрерывным временем.
Статистическое моделирование экономических систем
(метод Монте-Карло)
Оглавление
Видео:Цепи Маркова (видео 12) | Теория информации | ПрограммированиеСкачать

Вступление
На прошлой лекции мы начали рассматривать вероятностные модели.
Первая группа моделей, которые мы рассмотрели, относится к системам с конечным числом состояний, в которых переходы из состояния в состояние осуществляются в дискретные моменты времени (заранее заданные и, как правило, с равными промежутками).
С такими системами связывается матрица переходных вероятностей. Если эти вероятности постоянны (не зависят от времени), то цепь Маркова называется однородной. Кроме этого должен быть задан вектор начальных вероятностей.
Была дана формула, которая позволяет получить вектор вероятностей оказаться в том или ином состоянии после k-го шага функционирования процесса.
Видео:Случайные процессы 9. Марковские процессы.Скачать

Непрерывные цепи Маркова
Теперь рассмотрим процессы, в которых переход из узла в узел (из состояния в состояние) может произойти через любой случайный промежуток времени.
В этом случае мы должны ввести в рассмотрение непрерывное время, чтобы отслеживать (ловить) эти случайные моменты срабатывания переходов.
Марковский случайный процесс с дискретными состояниями и непрерывным временем называется при условии, что переход системы из состояния в состояние происходит не в фиксированные, а в случайные моменты времени.
Примеры
Поступление заявок на выполнение банковских операций.
Поломка машины в дороге.
Задание системы с конечным числом состояний и непрерывным временем наступления события (перехода из состояния в состояние)
Пусть система характеризуется n состояниями S0, S1, S2. Sn, а переход из состояния в состояние может осуществляться в любой момент времени. Обозначим через Pi(t) вероятность того, что в момент времени t система S будет находиться в состоянии Si (i = 0,1. n). Требуется определить для любого t вероятности состояний P0(t), P1 (t), …Pn(t). Очевидно, что
Определение плотности вероятностей перехода
Для процесса с непрерывным временем вместо переходных вероятностей Рij рассматриваются плотности вероятностей перехода λij, представляющие собой предел отношения вероятности перехода системы за время 

Если λij=const, то процесс называется однородным.
Если плотность вероятности λij(t), то процесс — неоднородный.
При рассмотрении непрерывных марковских процессов принято представлять переходы системы S из состояния в состояние как происходящие под влиянием некоторых потоков событий.
Потоки событий
Поток событий – последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.
В предыдущем примере – это поток отказов машины и поток восстановлений. Другие примеры: поток заявок в банкомат, поток покупателей в магазине, поток документов и т. д.
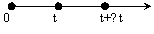
Поток событий можно наглядно изобразить рядом точек на оси времени Ot (рис. 1).
Рис. 1
Положение каждой точки случайно, и здесь изображена лишь какая-то одна реализация потока.
Интенсивность потока событий (λ) – это среднее число событий, приходящееся на единицу времени.
Пусть задан момент времени t и промежуток времени 
Обозначим 

Тогда 
Свойства потока событий
Рассмотрим некоторые свойства (виды) потоков событий.
Различают следующие основные свойства, которыми могут обладать случайные потоки событий:
- стационарность;
- ординарность;
- отсутствие последействия.
Стационарность
Свойство стационарности проявляется в том, что вероятность попадания того или иного числа событий на участок времени 
В частности, интенсивность стационарного потока постоянна λ=const. Поток событий неизбежно имеет сгущения или разрежения, но они не носят закономерного характера, и среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени.
Реальные потоки событий в экономике предприятия являются в действительности стационарными лишь на ограниченных участках времени. Поэтому, чтобы применить свойство стационарности, модели исследуют на ограниченных участках времени.
Ординарность
Свойство ординарности потока присутствует, если вероятность попадания на элементарный участок времени двух и более событий пренебрежимо мала по сравнению с длиной этого участка. Свойство ординарности означает, что за малый промежуток времени практически невозможно появление более одного события. Поток, обладающий свойством ординарности, называют ординарным.
Можно сказать, что для любого t на сколь угодно малом промежутке 
Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу. Иначе говоря, два события не происходят в один и тот же момент времени. Например, две машины не подъедут одновременно к стоянке, два человека не подойдут к банкомату, не обратятся с запросом к одной и той же БД и т.д.
За промежуток времени 
- ни одного события;
- 1 событие;
- > 1 события.
Если рассмотреть очень маленький промежуток времени 





По природе вероятности можно записать
Последним слагаемым пренебрегаем в виду его малости.
Можно сформулировать свойство ординарности таким образом: для любого момента времени t можно указать две вероятности: 

Реальные потоки событий в различных экономических системах либо являются ординарными, либо могут быть достаточно просто приведены к ординарным.
Для ординарных потоков интенсивность (математическое ожидание числа событий в единицу времени) (число событий может быть либо 0, либо 1)
Таким образом, интенсивность потока – это вероятность появления одного события на бесконечно малом промежутке времени. На практике интенсивность замеряют на некотором конечном промежутке времени и она приводится к этому промежутку.
Отсутствие последействия
Данное свойство потока состоит в том, что для любых непересекающихся участков времени 

Например, поставили сачок в двух местах реки. Можно ли утверждать, что если в первый сачок поймали 10 рыб, то и во второй попадутся 10 рыб?
Простейший поток
Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами:
- стационарен;
- ординарен;
- не имеет последействия.
Простейший поток имеет наиболее простое математическое описание. Он играет среди потоков такую же особую роль, как и закон нормального распределения среди других законов распределения. А именно, при наложении достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.
Если поток событий не имеет последействия, ординарен, но не стационарен, то его называют нестационарным пуассоновским потоком, а его интенсивность зависит от времени, т. е. 
Если поток событий удовлетворяет описанным выше свойствам, то справедлива теорема Цинлара.
Теорема. Пусть <N (t), 



а — среднее число событий, приходящееся на промежуток времени.
Для простейшего потока 


Отметим еще одно важное свойство простейшего потока событий. Промежуток времени t между соседними событиями распределен по показательному закону, а его среднее значение T и среднее квадратичное отклонение равны.
Для простейшего потока с интенсивностью λ=const интервал T между соседними событиями имеет так называемое показательное (экспоненциальное) распределение с плотностью
Для случайной величины T, имеющей показательное распределение, математическое ожидание mT есть величина, обратная параметру, а среднее квадратичное отклонение σT равно математическому ожиданию
Если в системе все потоки пуассоновские, то процесс, протекающий в системе S, будет марковским. И к нему применима теория непрерывных цепей Маркова.
Задача
Банкомат обслуживает одного человека в среднем 2 мин. К банкомату подходит в среднем 20 чел/ч. Считая поток клиентов к банкомату и поток выдачи денег из банкомата простейшими пуассоновскими, определить интенсивности этих потоков в одних единицах измерения (единиц/мин).

μ – интенсивность потока выдачи денег = 0,5 операции/мин.
Модель 8. Гараж-непрерывный
Автомобиль может находиться в двух состояниях – Исправен S1 или Ремонт S2. Поток событий, при котором автомобиль переходит из состояния Исправен в состояние Ремонт, является простейшим и характеризуется заданной интенсивностью λ, которую можно трактовать как количество поломок (отказов) в единицу времени. Поток восстановлений автомобиля также является простейшим и характеризуется заданной интенсивностью µ, которую можно трактовать как количество отремонтированных машин в единицу времени.
Рис. 2
Интенсивность потока отказов – λ.
Интенсивность потока восстановлений – μ.
Введем вектор вероятностей наступления событий
Начинаем выписывать производные:
Поясним смысл слагаемых в правой части этих выражений.
Событие (состояние) S1 наступает за счет того, что осуществляется переход из узла (состояния) S2 с интенсивностью μ, таким образом 1-е слагаемое показывает приращение вероятности, а уменьшение вероятности происходит от того, что осуществляется обратный переход к другому узлу с интенсивностью.
Пояснение на примере автомобиля. p1(t)– вероятность того, что автомобиль исправен, может быть определено как отношение промежутка нахождения в исправном состоянии на общее время протекания процесса. Что увеличивает промежуток исправного состояния? Переход из неисправного состояния в исправное с интенсивностью μ. А что уменьшает этот промежуток? Соответственно, обратный переход с интенсивностью. Если автомобили ломаются и чинятся с одинаковой интенсивностью, то можно предположить, что вероятности нахождения в обоих состояниях будут равны 1/2.
Если автомобили ломаются часто, а ремонт происходит медленно, то вероятность быть в неисправном состоянии будет больше чем в исправном.
Таким образом, изменение вероятности p1(t) (т. е. производная функции) увеличивается за счет выхода из ремонта и уменьшается за счет нахождения в ремонте. Это и отражают слагаемые в 1-м уравнении (соответственно со знаком «+» и «–»).
p2(t) – вероятность того, что автомобиль неисправен, может быть определено как отношение времени неисправного состояния на общее время протекания процесса.
Если сложим эти равенства, то получим
Интегрируя ДУ, получим, 
Если забудем, что функции – это вероятности, то получим систему ДУ, которые можно решить и получить законы вероятности нахождения в состояниях.
Одно из ДУ можно заменить соотношением вида, т. е., например, решать такую систему уравнений
Что может интересовать исследователя при решении таких ДУ?
Например, устойчивые решения, т. е. параметры, при которых имеют место устойчивые решения. То есть если есть устойчивое решение, то переходные процессы заканчиваются и, начиная с некоторого T*, функции p1(t),p2(t) выходят на стационарное значение (финальная вероятность).
Таким образом исследователя может интересовать, можно ли заранее предсказать, что система выйдет на стационар. И если да, то чему он будет равен.
Другое направление исследования – это собственно сами эти переходные процессы.
Если в рассмотренном примере считать, что описаны два возможных состояния автомобиля, то можно определить подвижной состав для автопредприятия. Та же ситуация с оборудованием, со штатным составом сотрудников и пр.
Уравнения Колмогорова
Пусть система характеризуется n состояниями S0, S1, S2. Sn, а переход из состояния в состояние может осуществляться в любой момент времени и является простейшим потоком событий. Обозначим через Рi(t) вероятность того, что в момент времени t система S будет находиться в состоянии Si(i = 0,1. n). Требуется определить для любого t вероятности состояний P0(t), P1 (t), …Pn(t).
Прежде всего, построим граф состояний системы.
Итак, на систему, находящуюся в состоянии Si, действует простейший поток событий. Как только появится первое событие этого потока, происходит «перескок» системы из состояния Si в состояние Sj(на графе состояний по стрелке Si
Для наглядности на графе состояний системы у каждой дуги проставляют интенсивности того потока событий, который переводит систему по данной дуге (стрелке). λij– интенсивность потока событий, переводящий систему из состояния Si в Sj. Такой граф называется размеченным.
Уравнения Колмогорова представляют собой систему ДУ для определения вероятностей Pi(t)
Слагаемые вида 
Производная вероятности каждого состояния равна сумме всех потоков вероятности, идущих из других состояний в данное, и минус сумма всех потоков вероятности, идущих из данного состояния в другие.
Сформулируем мнемоническое правило, по которому в ДУ включаются те или иные слагаемые и те или иные знаки.
К этой системе можно добавить нормирующее уравнение:
Это уравнение дает возможность составить на одно ДУ меньше.
Систему можно решить вручную или с помощью компьютера.
Если записать ДУ Колмогорова для системы «Гараж», то получатся именно такие уравнения, которые мы выписали исходя из эмпирических рассуждений.
Финальные вероятности состояний
Если процесс, протекающий в системе, длится достаточно долго, то имеет смысл говорить о предельном поведении вероятностей P1 (t), P2 (t)… при 
Что будет происходить с вероятностями состояний при 
где n – конечное число состояний системы.
Финальные вероятности состояний – это уже не переменные величины (функции времени), а постоянные числа. Очевидно, что
Говорят, что в системе S устанавливается предельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятности состояний уже не меняются. Система, для которой существуют финальные вероятности, называется эргодической, а соответствующий случайный процесс — эргодическим.
Финальные вероятности состояний (если они существуют) могут быть получены путем решения системы линейных алгебраических уравнений, которые получаются из дифференциальных уравнений Колмогорова, если приравнять производные к нулю, а вероятностные функции состояний P1(t), P2(t)… в правых частях уравнений заменить соответственно на неизвестные финальные вероятности p 1, p 2 …
Финальная вероятность состояния Si – это, по существу, среднее относительное время пребывания системы в этом состоянии.
Сделать предположения, что будет с системой, в некоторых случаях можно по графу
Пример 1.
Например, рассмотрим граф системы:
Здесь мы видим однонаправленное движение (ухудшение или улучшение). Глядя на граф можно сказать, что в будущем система обязательно скатится в состояние 4, 5 или 6 и там останется (стационар).
Пример 2.
Здесь циклическое повторение событий.
На данном графе случайные блуждания из состояния в состояние.
Эргодичность может быть не по отношению ко всем узлам системы. Можно эргодическое поведение выделить в отдельную систему.
Пример. Составление ДУ Колмогорова
Система имеет размеченный граф. В начальный момент система находилась в состоянии S1.
Написать над дугами обозначения интенсивностей, составить систему ДУ Колмогорова. Реализовать ее в среде MVS и найти финальные вероятности.
Граф после разметки
ДУ для состояния S1:
Задание для самостоятельной работы.
Дописать систему ДУ Колмогорова.
Как найти финальные вероятности системы?
Вернемся к примеру состояний автомобиля (модель 8).
Мы выписали ДУ для вероятностей состояний исходя из здравого смысла. Но, зная уравнения Колмогорова, которые теоретически строго доказаны, мы видим, что полученная система уравнений соответствует этим уравнениям.
У нас записана система ДУ 1-го порядка, однородная с постоянными коэффициентами. Условие стационара для такой системы – равенство нулю правой части.
Это уравнения зависимые, т. к. в сумме дают 0.
Поэтому вместо одного используем равенство p1+p2=1, где p1, p2– финальные вероятности, т. е. система будет иметь вид:
Решив эту систему относительно p1 и p2, получим финальные вероятности системы:
Процессы гибели и размножения
Особый раздел теории — так называемые процессы гибели и размножения.
Встречается в разнообразных практических задачах.
Марковский процесс с дискретными состояниями S0, S1, S2. Sn называется процессом гибели и размножения, если все состояния можно вытянуть в одну цепочку, в которой каждое из средних состояний (S0, S1, S2. Sn) может переходить только в соседние состояния, которые, в свою очередь, переходят обратно, а крайние состояния (S0, Sn) переходят только в соседние состояния (рис. 3).
Рис. 3. Граф состояний для процесса гибели и размножения
Название взято из биологических задач, где состояние популяции Sk означает наличие в ней k единиц особей.
Переход вправо связан с размножением единиц, а влево — с их гибелью.
У λ и μ индекс того состояния, из которого стрелка выходит.
С состоянием Sk связана неслучайная величина Xk: которая означает следующее: если система S в момент времени t находится в состоянии Sk, то дискретная случайная величина X(t), связанная с функционированием системы, принимает значение k. Таким образом, получаем случайный процесс X(t), который в случайные, заранее неизвестные моменты времени скачком изменяет свое состояние.
Марковским процессом гибели и размножения с непрерывным временем называется такой случайный процесс, который может принимать только целые неотрицательные значения. Изменения этого процесса могут происходить в любой момент времени, т. е. в любой момент времени он может либо увеличиться на единицу, либо уменьшиться на единицу, либо остаться неизменным.
В практике встречаются процессы чистого размножения и чистой гибели. Процессом чистого размножения называется такой процесс гибели и размножения, у которого интенсивности всех потоков гибели равны нулю; аналогично процессом чистой гибели называется такой процесс гибели и размножения, у которого интенсивности всех потоков размножения равны нулю.
Пример
Рассмотрим эксплуатацию компьютеров в вычислительном центре. Интенсивность приобретения новых компьютеров равна 
Пример
Процесс чистого размножения – производство товаров.
Видео:Цепи МарковаСкачать

Статистическое моделирование экономических систем
(метод Монте-Карло)
Теоретические основы метода
Метод статистического моделирования (или метод Монте-Карло) – это способ исследования поведения вероятностных систем в условиях, когда неизвестны в полной мере внутренние взаимодействия в этих системах.
Метод основан на многократных испытаниях построенной вероятностной математической модели с последующей статистической обработкой полученных результатов.
Цель метода – определение числовых характеристик рассматриваемого процесса в виде статистических оценок его параметров.
Процесс моделирования функционирования экономической системы сводится к машинной имитации изучаемого процесса со всеми сопровождающими его случайностями.
Закон больших чисел
Основой метода статистического моделирования является закон больших чисел (ЗБЧ). ЗБЧ доказывает для различных условий сходимость по вероятности средних значений результатов большого числа наблюдений к некоторым постоянным величинам.
Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений.
Теоретическим обоснованием этого замечательного свойства случайных явлений является закон больших чисел. Названием «закон больших чисел» объединена группа теорем, устанавливающих устойчивость средних результатов большого количества случайных явлений и объясняющих причину этой устойчивости.
Центральная предельная теорема объясняет широкое распространение нормального закона распределения. Теорема утверждает, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин с конечными дисперсиями, закон распределения этой случайной величины оказывается практически нормальным законом.
Предположим какой-то случайный процесс состоит из последовательности элементарных независимых процессов. Длительность каждого процесса ti – является случайной величиной, распределенной по неизвестному закону с МО ti и дисперсией 

Теорема (центральная предельная). Если сделать предельный переход, то распределение случайной величины t будет стремиться к нормальному с МО, равным сумме МО ti и дисперсией, равной сумме дисперсий ti
Рассматривается в различных математических постановках в литературе по теории вероятностей.
Пояснение. Практический смысл.
Любые сложные работы на объектах экономики (ввод информации их документа в компьютер, проведение переговоров, ремонт оборудования и пр.) состоят из множества коротких последовательных элементарных работ. Причем количество их велико, и требования теоремы можно считать выполняющимися. Поэтому при оценках трудозатрат всегда справедливо предположение о том, что их продолжительность – это случайная величина, распределенная по нормальному закону.
Предельная теорема о суперпозиции (наложении) потоков
Предположим, что можно наблюдать k независимых потоков событий. В каждом потоке можно наблюдать mj элементарных событий. Интервалы между событиями – это независимые случайные величины, распределенные по неизвестному закону с МО 

Теорема. Если сделать предельный переход 
Пример.
Имеется некая крупная фирма. Клиенты – физические и юридические лица. Каждый имеет свое расписание (набор планов и дел) на значительном интервале времени. Однако если рассмотреть суммарный поток обращений клиентов к служащим фирмы, то интервал между двумя последовательными обращениями будет случайной величиной, распределенной по экспоненциальному закону.
Примеры потоков, имеющих показательное (экспоненциальное) распределение:
- время поступления заказа на предприятие;
- посещение покупателями магазина;
- телефонные разговоры;
- срок службы деталей и узлов в компьютере.
Схема решения задачи методом статистического моделирования
- Разработка и построение структурной схемы процесса, выявление основных взаимосвязей.
- Формальное описание процесса.
- Моделирование случайных явлений (случайных событий, случайных величин, случайных функций), сопровождающих функционирование исследуемой системы.
- Моделирование функционирования системы – воспроизведение процесса в соответствии с разработанной структурной схемой и формальным описанием.
- Накопление результатов моделирования, статистическая обработка, анализ и обобщение.
Результаты, получаемые при статистическом моделировании подвержены экспериментальным ошибкам.
Экспериментальные ошибки в значительной степени зависят от точности моделирования случайных явлений, сопровождающих функционирование системы. Моделирование случайных явлений сводится к моделированию случайных событий, случайных величин, случайных функций. Так как случайные события и случайные функции могут быть представлены через случайные величины, то моделирование случайных событий и случайных функций проводится с помощью случайных величин.
Видео:Цепи МарковаСкачать

Моделирование случайных величин
Для моделирования случайной величины необходимо знать ее закон распределения.
Наиболее общим способом получения последовательности случайных чисел, распределенных по произвольному закону, является способ, основанный на формировании их из последовательности равномерно распределенных чисел на промежутке [0, 1].
Опишем этот способ более подробно на примере получения случайной величины с экспоненциальным распределением.
Экспоненциальное (показательное) распределение случайной величины задается плотностью распределения:


Существует связь между пуассоновским и экспоненциальным распределениями. Если случайная величина подчинена закону Пуассона и представляет собой число отказов в единицу времени, то случайная величина, которая определяет промежуток времени между двумя отказами, распределена по экспоненциальному закону. Чтобы получить величину этого интервала применяют следующий способ:
- Генерируется случайное равномерно распределенное число ξ на промежутке [0,1]. В среде MVS это можно сделать с помощью функции uniform (0,1).
- Для преобразования равномерно распределенного случайного числа в случайное число с заданным законом распределения F(t) надо решить уравнение вида. Если закон распределения задан плотностью распределения, то уравнение имеет вид.
Для показательного распределения уравнение имеет вид. Отсюда получаем величину 

Такие же соотношения получены и для других законов распределения
📸 Видео
Соколов Д. Д. - Теория случайный процессов - Марковские процессы с непрерывным временемСкачать

03 Марковские процессы с дискретным временемСкачать
Шкляев А.В. - Теория случайных процессов - 16. Марковские процессы с непрерывным временемСкачать

Соколов Д. Д. - Теория случайный процессов - Марковские цепи с непрерывным набором состоянийСкачать

Марковские процессы [1] // Александр БуфетовСкачать
![Марковские процессы [1] // Александр Буфетов](https://i.ytimg.com/vi/OmTz7EEs--4/0.jpg)
05 Марковские случайные процессы с непрерывным временемСкачать

Марковские процессы [2] // Александр БуфетовСкачать
![Марковские процессы [2] // Александр Буфетов](https://i.ytimg.com/vi/HyqSiO2kI5E/0.jpg)
06 Марковские случайные процессы с непрерывным временем Предельное распределениеСкачать

уравнение колмагороваСкачать

Случайные процессы 8 Марковские цепиСкачать

Зейфман А.И. - О свойствах решений прямой системы Колмогорова и оценках для марковских цепейСкачать

ЦОС Python #4: Марковские процессы в дискретном времениСкачать

Случайные процессы 11 Непрерывные цепи МарковаСкачать

Лекция 13. Непрерывные марковские процессы. 30.04.2021Скачать