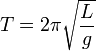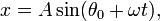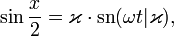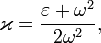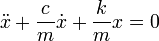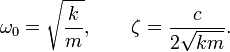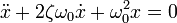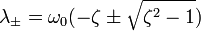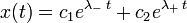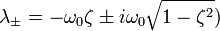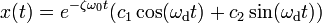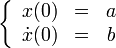| mg |
| φ |
| o |
| c |
| O’ |
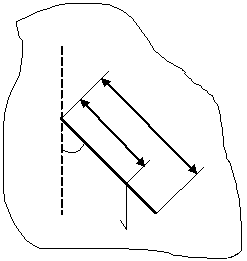
| Рисунок 3 3. Приведенная длина |
Физическим маятником называется любое тело, которое под действием силы тяжести может свободно качаться вокруг неподвижной горизонтальной оси, называемой осью качаний. Точка пересечения оси качаний с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса маятника (т. О на рис. 3). Очевидно, в положении равновесия центр масс маятника (т. С) находится на вертикальной прямой, проходящей через точку подвеса (φ = 0).
Движение маятника описывается основным уравнением динамики вращательного движения вокруг неподвижной оси:
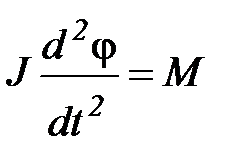
где J – момент инерции маятника относительно оси вращения, φ – угол отклонения маятника от положения равновесия, М – суммарный момент внешних сил, действующих на маятник относительно оси вращения.
В экспериментальных установках обычно моменты силы трения в оси и силы сопротивления воздуха пренебрежимо малы. Поэтому Мс = – mgd sinφ, где
d = │ОС│ – расстояние от оси качания до центра масс, m – масса маятника,
g – ускорение свободного падения, а знак » – » указывает на то, что момент силы тяжести стремится возвратить маятник в положение равновесия. Таким образом, уравнение движения маятника имеет вид:
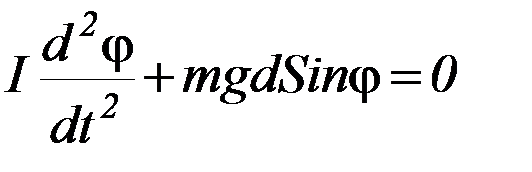
В случае малых отклонений маятника от положения равновесия (т.е. φ
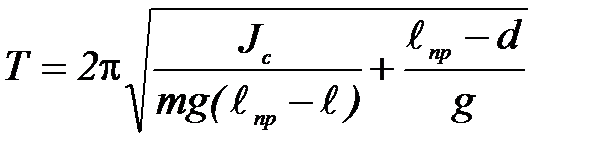
Из (П-7) имеем:
Тогда
Таким образом, период колебаний физического маятника не изменяется при перемещении оси качаний в центр качаний.
Видео:9. Колебания физического маятникаСкачать

Уравнение колебаний маятника
Рис.1
Исследуем выражение (2) в зависимости от разности фаз (φ2 — φ1):
1) φ2 — φ1 = ±2mπ (m = 0, 1, 2, . ), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 — φ1 = ±(2m+1)π (m = 0, 1, 2, . ), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω
23 Колебания физического маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
— угол отклонения маятника от равновесия;
— начальный угол отклонения маятника;
— масса маятника;
— расстояние от точки подвеса до центра тяжести маятника;
— радиус инерции относительно оси, проходящей через центр тяжести.
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:

[править] Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
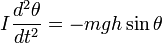
Полагая 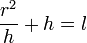
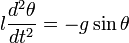
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 

[править] Центр качания физического маятника
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен 
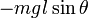
[править] Теорема Гюйгенса
[править] Формулировка
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
[править] Доказательство
Вычислим приведенную длину для нового маятника:
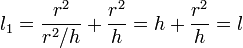
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
[править] Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на 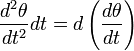
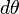
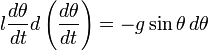
Интегрируя это уравнение, получаем.
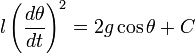
где 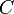
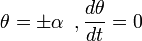
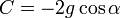
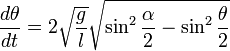
Отделяем переменные и интегрируем это уравнение:
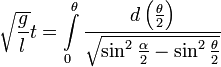
Удобно сделать замену переменной, полагая 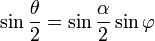
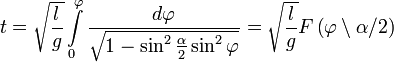
Здесь 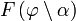
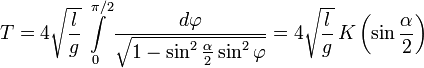
Здесь 
[править] Период малых колебаний физического маятника
Если амплитуда колебаний 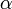
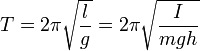
24 Колебания математического маятника
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 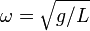
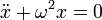
[править] Решения уравнения движения
[править] Гармонические колебания
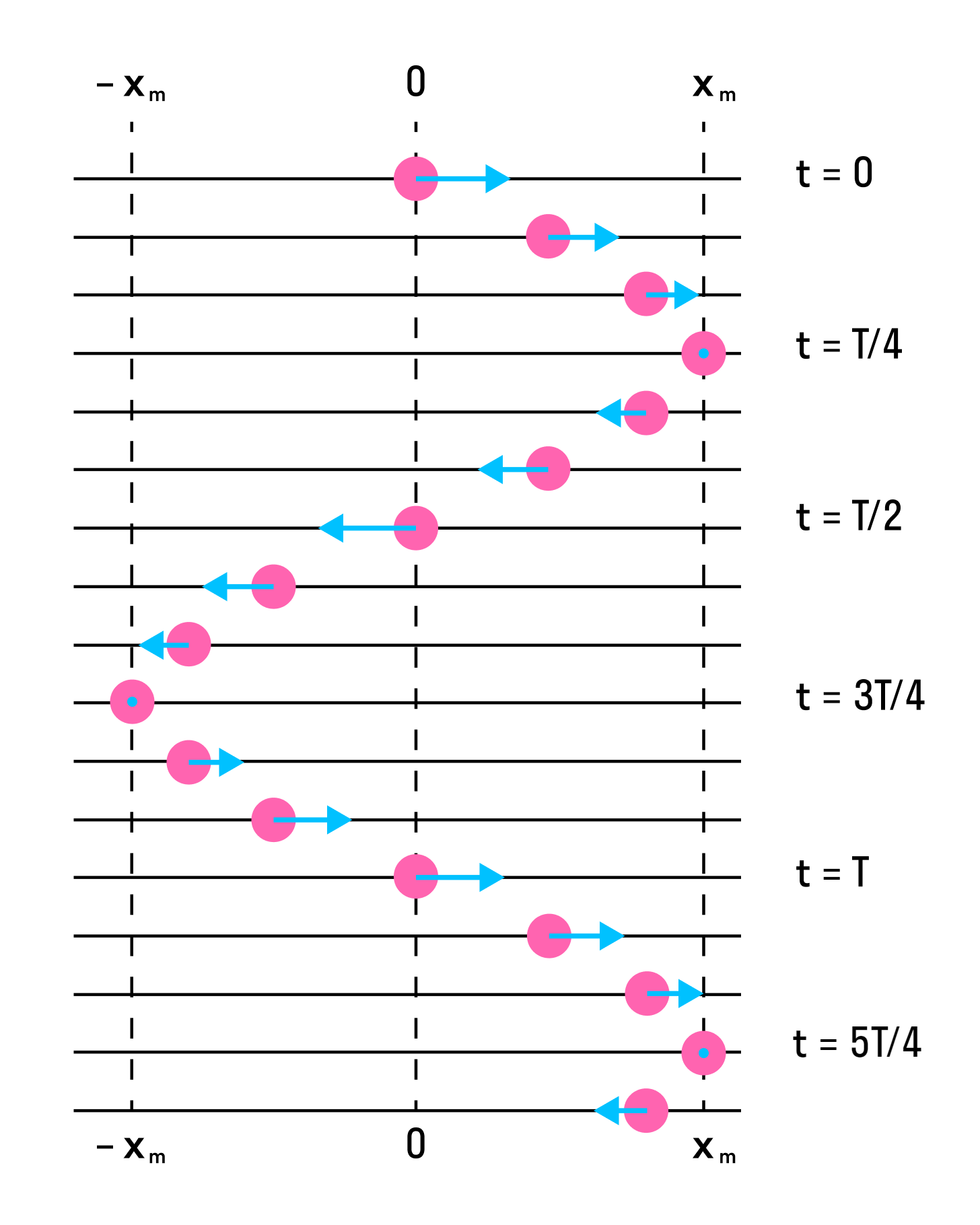
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
[править] Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 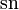

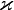
Параметр 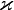
где 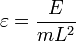
Период колебаний нелинейного маятника
где K — эллиптический интеграл первого рода.
[править] Движение по сепаратрисе
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.
25 Затухающие колебания. Зависимость амплитуды от времени.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 
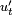
Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
где Fc — сила сопротивления, Fy — сила упругости
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
Сделав замену x = e λt , получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
[править] Решения
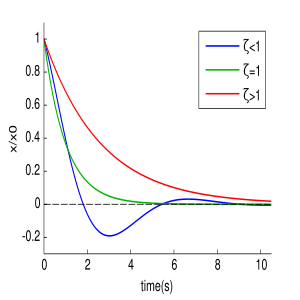
Зависимость графиков колебаний от значения ζ.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если 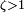
В этом случае колебания с самого начала экспоненциально затухают.
- Граница апериодичности
Если 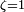
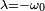
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если 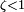
Тогда решением исходного дифференциального уравнения является
Где 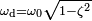
Константы c1 и c2 в каждом из случаев определяются из начальных условий:
26 Вынужденные колебания. Понятие резонанса.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 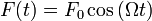
Видео:Математические и пружинные маятники. 11 класс.Скачать

Гармонические колебания
О чем эта статья:
9 класс, 11 класс, ЕГЭ/ОГЭ
Видео:математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Видео:Физический маятникСкачать

Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать

Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Видео:физический маятникСкачать

Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Видео:ЛР 1.05 Изучение колебаний физического маятникаСкачать

Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.
Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.
Формула периода колебаний
T = t/N
N — количество колебаний [—]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
N — количество колебаний [—]
Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .
Она используется в уравнении гармонических колебаний:
Видео:Колебания математического маятникаСкачать

Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
Уравнение гармонических колебаний
x — координата в момент времени t [м]
t — момент времени [с]
(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ
Фаза колебаний
t — момент времени [с]
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
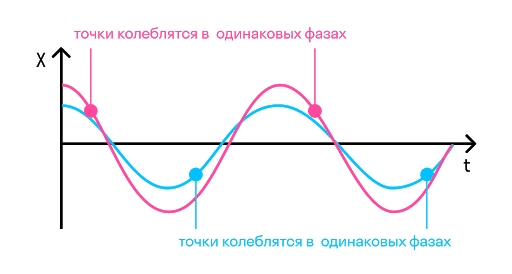
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Видео:Колебания. Физический маятник. Период и частота колебаний физического маятника.Скачать

Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника
l — длина нити [м]
g — ускорение свободного падения [м/с 2 ]
На планете Земля g = 9,8 м/с 2
Видео:Колебания математического и пружинного маятников. 9 класс.Скачать

Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
Формула периода колебания пружинного маятника
m — масса маятника [кг]
k — жесткость пружины [Н/м]
Видео:Математический маятник или откуда формула периодаСкачать

Закон сохранения энергии для гармонических колебаний
Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.
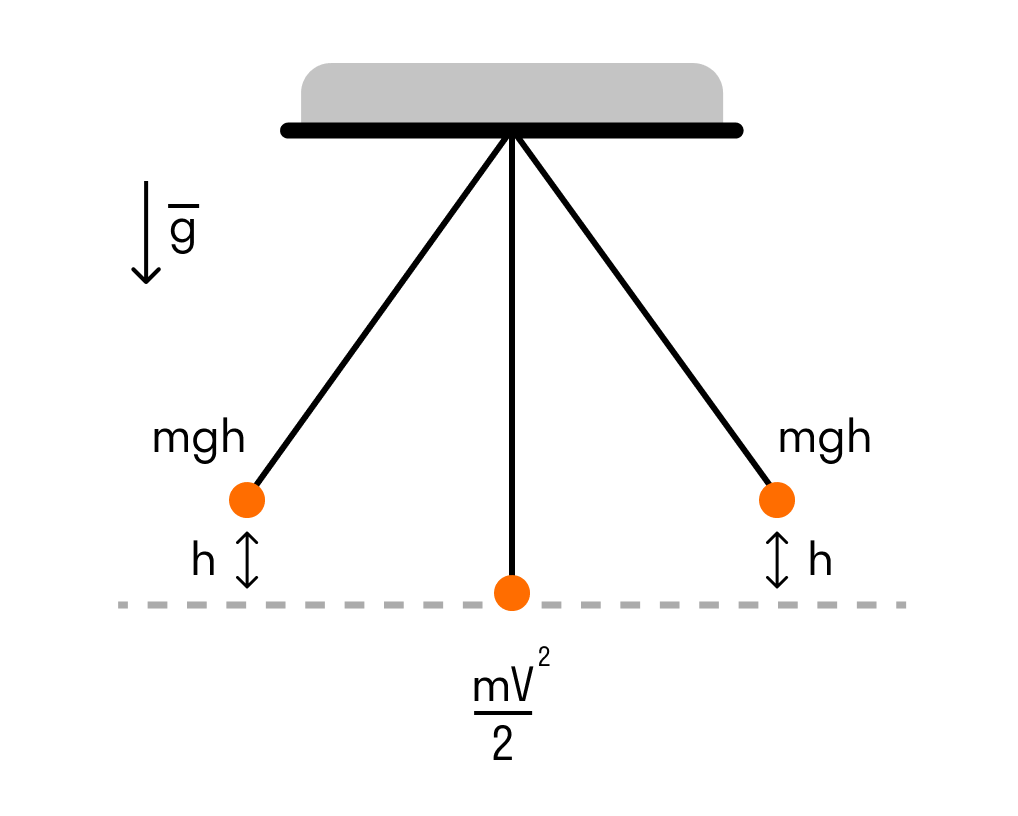
Рассмотрим его на примере математического маятника.
- Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
- Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
💥 Видео
Почти всё о маятникеСкачать

Видеоурок по физике "Математический и пружинный маятники"Скачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Малые колебанияСкачать

Механика. Л 10.2. Колебания. Вывод дифф уравнений колебаний математического и физического маятниковСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Негармонические колебания физического маятникаСкачать

Классические уравнения | физический маятник | аналогия с математическим маятникомСкачать

Классические уравнения | физический маятник | вывод при помощи уравнения Эйлера - ЛагранжаСкачать

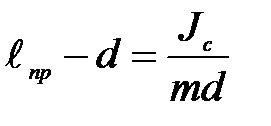
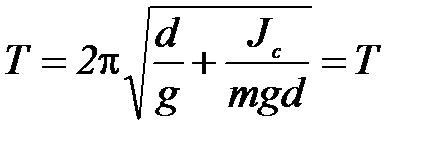
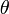 — угол отклонения маятника от равновесия;
— угол отклонения маятника от равновесия; — масса маятника;
— масса маятника;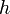 — расстояние от точки подвеса до центра тяжести маятника;
— расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.
— радиус инерции относительно оси, проходящей через центр тяжести.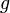 — ускорение свободного падения.
— ускорение свободного падения.