Максимумов и минимумов уравнение при интерференции

Видео:Урок 414. Интерференция светаСкачать

Интерференция волн.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: интерференция света.

В предыдущем листке, посвящённом принципу Гюйгенса, мы говорили о том, что общая картина волнового процесса создаётся наложением вторичных волн. Но что это значит — «наложением»? В чём состоит конкретный физический смысл наложения волн? Что вообще происходит, когда в пространстве одновременно распространяются несколько волн? Этим вопросам и посвящён данный листок.

Видео:Физика 11 класс (Урок№16 - Интерференция света.)Скачать

Сложение колебаний.

Сейчас мы будем рассматривать взаимодействие двух волн. Природа волновых процессов роли не играет — это могут быть механические волны в упругой среде или электромагнитные волны (в частности, свет) в прозрачной среде или в вакууме.

Опыт показывает, что волны складываются друг с другом в следующем смысле.

Принцип суперпозиции. Если две волны накладываются друг на друга в определённой области пространства, то они порождают новый волновой процесс. При этом значение колеблющейся величины в любой точке данной области равно сумме соответствующих колеблющихся величин в каждой из волн по отдельности.

Например, при наложении двух механических волн перемещение частицы упругой среды равно сумме перемещений, создаваемых в отдельности каждой волной. При наложении двух электромагнитных волн напряжённость электрического поля в данной точке равна сумме напряжённостей в каждой волне (и то же самое для индукции магнитного поля).

Разумеется, принцип суперпозиции справедлив не только для двух, но и вообще для любого количества накладывающихся волн. Результирующее колебание в данной точке всегда равно сумме колебаний, создаваемых каждой волной по отдельности.

Мы ограничимся рассмотрением наложения двух волн одинаковой амплитуды и частоты. Этот случай наиболее часто встречается в физике и, в частности, в оптике.

Оказывается, на амплитуду результирующего колебания сильно влияет разность фаз складывающихся колебаний. В зависимости от разности фаз в данной точке пространства две волны могут как усиливать друг друга, так и полностью гасить!

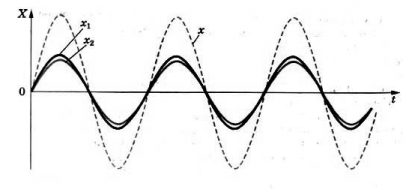
Предположим, например, что в некоторой точке фазы колебаний в накладывающихся волнах совпадают (рис. 1 ).

Рис. 1. Волны в фазе: усиление колебаний

Мы видим, что максимумы красной волны приходятся в точности на максимумы синей волны, минимумы красной волны — на минимумы синей (левая часть рис. 1 ). Складываясь в фазе, красная и синяя волны усиливают друг друга, порождая колебания удвоенной амплитуды (справа на рис. 1 ).

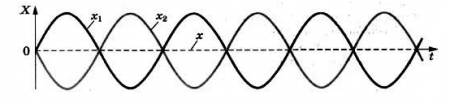
Теперь сдвинем синюю синусоиду относительно красной на половину длины волны. Тогда максимумы синей волны будут совпадать с минимумами красной и наоборот — минимумы синей волны совпадут с максимумами красной (рис. 2 , слева).

Рис. 2. Волны в противофазе: гашение колебаний

Колебания, создаваемые этими волнами, будут происходить, как говорят, в противофазе — разность фаз колебаний станет равна . Результирующее колебание окажется равным нулю, т. е. красная и синяя волны попросту уничтожат друг друга (рис. 2 , справа).

Видео:Волны Основные понятия.Интерференция.Разность хода.Условие максимума и минимумаСкачать

Когерентные источники.

Пусть имеются два точечных источника, создающие волны в окружающем пространстве. Мы полагаем, что эти источники согласованы друг с другом в следующем смысле.

Когерентность. Два источника называются когерентными, если они имеют одинаковую частоту и постоянную, не зависящую от времени разность фаз. Волны, возбуждаемые такими источниками, также называются когерентными.

Итак, рассматриваем два когерентных источника и . Для простоты считаем, что источники излучают волны одинаковой амплитуды, а разность фаз между источниками равна нулю. В общем, эти источники являются «точными копиями» друг друга (в оптике, например, источник служит изображением источника в какой-либо оптической системе).

Наложение волн, излучённых данными источниками, наблюдается в некоторой точке . Вообще говоря, амплитуды этих волн в точке не будут равны друг другу — ведь, как мы помним, амплитуда сферической волны обратно пропорциональна расстоянию до источника, и при разных расстояниях и амплитуды пришедших волн окажутся различными. Но во многих случаях точка расположена достаточно далеко от источников — на расстоянии гораздо большем, чем расстояние между самими источниками. В такой ситуации различие в расстояниях и не приводит к существенному отличию в амплитудах приходящих волн. Следовательно, мы можем считать, что амплитуды волн в точке также совпадают.

Видео:Урок 380. Интерференция волнСкачать

Условие максимума и минимума.

Однако величина , называемая разностью хода, имеет важнейшее значение. От неё самым решительным образом зависит то, какой результат сложения приходящих волн мы увидим в точке .

Рис. 3. Усиление колебаний в точке P

В ситуации на рис. 3 разность хода равна длине волны . Действительно, на отрезке укладываются три полных волны, а на отрезке — четыре (это, конечно, лишь иллюстрация; в оптике, например, длина таких отрезков составляет порядка миллиона длин волн). Легко видеть, что волны в точке складываются в фазе и создают колебания удвоенной амплитуды — наблюдается, как говорят, интерференционный максимум.

Ясно, что аналогичная ситуация возникнет при разности хода, равной не только длине волны, но и любому целому числу длин волн.

Условие максимума. При наложении когерентных волн колебания в данной точке будут иметь максимальную амплитуду, если разность хода равна целому числу длин волн:

Теперь посмотрим на рис. 4 . На отрезке укладываются две с половиной волны, а на отрезке -три волны. Разность хода составляет половину длины волны ( d=lambda /2[/math] ).

Рис. 4. Гашение колебаний в точке P

Теперь нетрудно видеть, что волны в точке складываются в противофазе и гасят друг друга — наблюдается интерференционный минимум. То же самое будет, если разность хода окажется равна половине длины волны плюс любое целое число длин волн.

Условие минимума.
Когерентные волны, складываясь, гасят друг друга, если разность хода равна полуцелому числу длин волн:

Равенство (2) можно переписать следующим образом:

Поэтому условие минимума формулируют ещё так: разность хода должна быть равна нечётному числу длин полуволн.

Видео:Интерференция механических волн. 11 класс.Скачать

Интерференционная картина.

А что, если разность хода принимает какое-то иное значение, не равное целому или полуцелому числу длин волн? Тогда волны, приходящие в данную точку, создают в ней колебания с некоторой промежуточной амплитудой, расположенной между нулём и удвоенным значением 2A амплитуды одной волны. Эта промежуточная амплитуда может принимать все значения от 0 до 2A по мере того, как разность хода меняется от полуцелого до целого числа длин волн.

Таким образом, в той области пространства, где происходит наложение волн когерентных источников и , наблюдается устойчивая интерференционная картина — фиксированное не зависящее от времени распределение амплитуд колебаний. А именно, в каждой точке данной области амплитуда колебаний принимает своё значение, определяемое разностью хода приходящих сюда волн, и это значение амплитуды не меняется со временем.

Такая стационарность интерференционной картины обеспечивается когерентностью источников. Если, например, разность фаз источников будет постоянно меняться, то никакой устойчивой интерференционной картины уже не возникнет.

Теперь, наконец, мы можем сказать, что такое интерференция.

Интерференция — это взаимодействие волн, в результате которого возникает устойчивая интерференционная картина, то есть не зависящее от времени распределение амплитуд результирующих колебаний в точках области, где волны накладываются друг на друга.

Если волны, перекрываясь, образуют устойчивую интерференционную картину, то говорят попросту, что волны интерферируют. Как мы выяснили выше, интерферировать могут только когерентные волны. Когда, например, разговаривают два человека, то мы не замечаем вокруг них чередований максимумов и минимумов громкости; интерференции нет, поскольку в данном случае источники некогерентны.

На первый взгляд может показаться, явление интерференции противоречит закону сохранения энергии — например, куда девается энергия, когда волны полностью гасят друг друга? Но никакого нарушения закона сохранения энергии, конечно же, нет: энергия просто перераспределяется между различными участками интерференционной картины. Наибольшее количество энергии концентрируется в интерференционных максимумах, а в точки интерференционных минимумов энергия не поступает совсем.

На рис. 5 показана интерференционная картина, созданная наложением волн двух точечных источников и . Картина построена в предположении, что область наблюдения интерференции находится достаточно далеко от источников. Пунктиром отмечена ось симметрии интерференционной картины.

Рис. 5. Интерференция волн двух точечных источников

Цвета точек интерференционной картины на этом рисунке меняются от чёрного до белого через промежуточные оттенки серого. Чёрный цвет — интерференционные минимумы, белый цвет — интерференционные максимумы; серый цвет — промежуточное значение амплитуды, и чем больше амплитуда в данной точке, тем светлее сама точка.

Обратите внимание на прямую белую полосу, которая идёт вдоль оси симметрии картины. Здесь расположены так называемые центральные максимумы. Действительно, любая точка данной оси равноудалена от источников (разность хода равна нулю), так что в этой точке будет наблюдаться является интерференционный максимум.

Остальные белые полосы и все чёрные полосы слегка искривлены; можно показать, что они являются ветвями гипербол. Однако в области, расположенной на большом расстоянии от источников, кривизна белых и чёрных полос мало заметна, и выглядят эти полосы почти прямыми.

Интерференционный опыт, изображённый на рис. 5 , вместе с соответствующим методом расчёта интерференционной картины называется схемой Юнга. Эта схема лежит в основе знаменитного
опыта Юнга (речь о котором пойдёт в теме Дифракция света). Многие эксперименты по интерференции света так или иначе сводятся к схеме Юнга.

В оптике интерференционную картину обычно наблюдают на экране. Давайте ещё раз посмотрим на рис. 5 и представим себе экран, поставленный перпендикулярно пунктирной оси.
На этом экране мы увидим чередование светлых и тёмных интерференционных полос.

На рис. 6 синусоида показывает распределение освещённости вдоль экрана. В точке O, расположенной на оси симметрии, находится центральный максимум. Первый максимум в верхней части экрана, соседний с центральным, находится в точке A. Выше идут второй, третий (и такдалее) максимумы.

Рис. 6. Интерференционная картина на экране

Расстояние , равное расстоянию между любыми двумя соседними максимумами или минимумами, называется шириной интерференционной полосы. Сейчас мы займёмся нахождением этой величины.

Пусть источники находятся на расстоянии друг от друга, а экран расположен на расстоянии от источников (рис. 7 ). Экран заменён осью ; начало отсчёта , как и выше, отвечает центральному максимуму.

Рис. 7. Вычисление координат максимумов

Точки и служат проекциями точек и на ось и расположены симметрично относительно точки . Имеем: .

Точка наблюдения может находиться на оси (на экране) где угодно. Координату точки
мы обозначим . Нас интересует, при каких значениях в точке будет наблюдаться интерференционный максимум.

Волна, излучённая источником , проходит расстояние:

Теперь вспомним, что расстояние между источниками много меньше расстояния от источников до экрана: . Кроме того, в подобных интерференционных опытах координата точки наблюдения также гораздо меньше . Это означает, что второе слагаемое под корнем в выражении (3) много меньше единицы:

Раз так, можно использовать приближённую формулу:

Применяя её к выражению (4) , получим:

Точно так же вычисляем расстояние, которое проходит волна от источника до точки наблюдения:

Применяя к выражению (6) приближённую формулу (4) , получаем:

Вычитая выражения (7) и (5) , находим разность хода:

Пусть — длина волны, излучаемой источниками. Согласно условию (1) , в точке будет наблюдаться интерференционный максимум, если разность хода равна целому числу длин волн:

Отсюда получаем координаты максимумов в верхней части экрана (в нижней части максимумы идут симметрично):

При получаем, разумеется, (центральный максимум). Первый максимум рядом с центральным соответствует значению и имеет координату .Такой же будет и ширина интерференционной полосы:

Видео:Интерференция и дифракция. Подготовка к ЕГЭ по физике | Николай Ньютон. ТехноскулСкачать

Интерференция света

теория по физике 🧲 оптика

Для всех волн характерны явления интерференции и дифракции. Если свет — это волна, то для него также должны быть присущи эти явления. Так рассуждали ученые, которые считали, что свет имеет волновую природу. Первым привел экспериментальные доказательства интерференции и дифракции света Томас Юнг в 1801 году.

Это интересно! Явление интерференции света было описано и объяснено в 1801 году, но само понятие «интерференция света» было введено немного позже — в 1803 году.

Видео:Урок 420. Дифракция света. Дифракционная решеткаСкачать

Интерференция механических волн

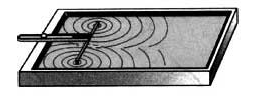
Чтобы лучше понять явление интерференции, сначала объясним его на примере механических волн, за которыми удобней наблюдать. Часто случается, что в среде одновременно распространяется несколько различных волн. К примеру, когда в комнате может одновременно находиться несколько источников звука. Что же происходит, когда волны пересекают друг друга? Объясним это на примере волн, образуемых на поверхности воды.

Если бросить в воду два камешка, образуются две круговые волны. Если наблюдать за их распространением, мы увидим, что каждая волна проходит сквозь другую. Причем она ведет себя так, как будто другой волны не существовало. Точно так же любое количество звуковых волн может одновременно распространяться в воздухе. И они не будут друг другу мешать. Множество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, которые улавливаются нами одновременно. При этом звуки не сливаются в шум: наши органы слуха способны легко отличить один звук от другого.

Теперь рассмотрим более подробно процесс, когда волны накладываются одна на другую. Для этого будем наблюдать волны на поверхности воды от двух брошенных в воду камней. При этом мы заметим, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если два гребня двух волн встречаются в одном месте, то в этом месте возмущение поверхности воды становится более сильным. Если же гребень одной волны встречается с впадиной другой, то поверхность воды в этом месте остается спокойной. Получается, что в каждой точке среды колебания, вызванные двумя волнами, складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.

Интерференция — сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды.

Чтобы выяснить, при каких условиях наблюдается интерференция волн, одновременно возбудим две круговые волны в ванночке с помощью двух шариков, прикрепленных к стержням, колеблющимся по гармоническому закону.

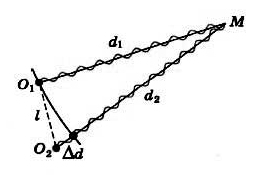
Теперь представим явление интерференции схематически. В любой точке М на поверхности воды будут складываться колебания, вызванные двумя волнами от источников O₁ и O₂ (см. рисунок ниже). Амплитуды колебаний, вызванных в точке М обеими волнами, будут различаться, если волны проходят различные пути d₁ и d₂. Но если расстояние l между источниками много меньше этих путей, то обе амплитуды можно считать приближенно одинаковыми.

Результат сложения волн, приходящих в точку М зависит от разности фаз между ними. Пройдя различные расстояния d₁ и d₂, волны имеют разность хода, определяемую формулой:

Когда разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой на один период. Так как за период волна проходит путь, равный ее длине волны, то в точке встречи двух волн фазы совпадают. Если в этой точке волны имеют гребни, то совпадают гребни, если впадины — совпадают впадины.

Условие минимумов и максимумов

Когда гребни волн на поверхности волны складываются в одной точке, их амплитуда резко возрастает. В этом случае говорят, что в этой точке образуется интерференционный максимум. Когда впадины волн на поверхности волны складываются в одной точке, их амплитуда резко уменьшается. В этом случае говорят, что в этой точке образуется интерференционный минимум. Интерференционные минимумы и максимумы образуются при соблюдении определенных условий.

Если разность хода волн равна нечетному числу полуволн, то в точке наложения этих волн образуется интерференционный минимум. Амплитуда колебаний в данной точке минимальна.

Δ d = ( 2 k + 1 ) λ 2 . .

Если разность хода волн равна целому числу волн, то в точке наложения этих волн образуется интерференционный максимум. Амплитуда колебаний в данной точке максимальна.

Если разность хода ∆d принимает промежуточное значение между λ и λ/2, амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важной примечательностью является то, что амплитуда колебаний в любой точке с течением времени не меняется. Поэтому на поверхности воды возникает определенное, постоянное во времени распределение амплитуд колебаний, которое называют интерференционной картиной.

Для формирования устойчивой интерференционной картины важно, чтобы источники волн имели одинаковую частоту, и разность фаз их колебаний не менялась с течением времени. Такие источники волн называют когерентными.

Когерентные волны — это волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.

Только когерентные волны при сложении формируют устойчивую интерференционную картину. Если же источники волн некогерентные, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет с течением времени изменяться. Поэтому амплитуда результирующих колебаний также будет непрерывно изменяться. В результате максимумы и минимумы в пространстве будут иметь неопределенное положение. Поэтому интерференционная картина получается размытой.

Распределение энергии при интерференции

Любая волна переносит энергию без переноса вещества. Но что же с этой энергией происходит при интерференции волн? Если волны встречаются друг с другом, энергия никуда не исчезает и не превращается в другие формы энергии. Она лишь перераспределяется таким образом, что в минимумах он не поступает совсем, поскольку концентрируется в максимумах.

Видео:Опыты по физике. Интерференция волнСкачать

Интерференция света

Ели свет — это поток волн, то должно наблюдаться явление интерференции. Однако получить интерференционную картину, при которой чередуются минимумы и максимумы с помощью двух независимых источников света (к примеру, двух ламп), невозможно. Включение второй лампы лишь увеличивает освещенность поверхности, но не создает картины из минимумов и максимумов. Это объясняется несогласованностью волн друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные, то есть когерентные световые волны. Они должны иметь одинаковые длины волн и постоянную во времени разность фаз в любой точке пространства.

Однако наблюдать интерференцию света все же можно. Вы ее наблюдали, когда пускали мыльные пузыри или рассматривали пленку нефти на поверхности воды.

Томас Юнг — первый из ученых, который предложил объяснить изменение цветов тонких пленок сложением волн. Согласно его предположению, одна волна отражается от наружной поверхности плёнки, а другая — от внутренней. При этом возникает явление, называемой интерференцией световых волн.

Усиление света происходит в том случае, если преломлённая волна запаздывает по сравнению с отражённой волной на целое число длин волн. Здесь действует условие максимумов, о котором мы говорили выше:

Если вторая волна запаздывает по сравнению с первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света. Здесь действует условие минимумов, о котором мы также уже говорили:

Δ d = ( 2 k + 1 ) λ 2 . .

Четкая интерференционная картина получается потому, что волны, отраженные от внутренней и внешней оболочки тонкой пленки, являются когерентными. Когерентность этих волн объясняется тем, что они являются частями одного и того же светового луча.

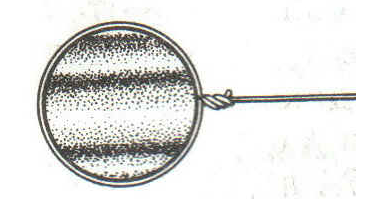
Юнг сделал вывод, что многообразие цветов на мыльной пленке связано с разницей в длине волны. Если плёнка имеет неоднородную толщину, то при освещении её белым светом появляются различные цвета.

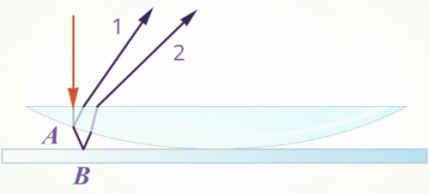
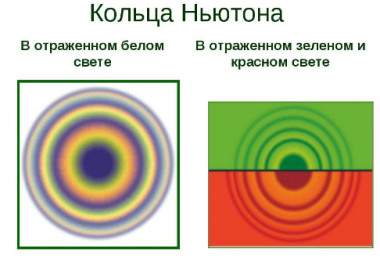
Простую интерференционную картину также можно получить, если положить на стеклянную поверхность плоско-выпуклую линзу, сферическая поверхность которой имеет большой радиус кривизны. Интерференционная картина, полученная таким способом, носит название колец Ньютона.

Исаак Ньютон исследовал интерференционную картину, получаемую в тонкой прослойке воздуха между стеклом и линзой, не только в белом свете, но и при освещении линзы монохроматическими лучами. Так он установил, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному. Так, красные кольца имеют максимальный радиус. Расстояние между соседними кольцами уменьшаются с увеличением их радиусов.

Ньютону удалось получить кольца, но их появление он объяснить не смог. Но это удалось сделать Юнгу. Проведенный им опыт показал, что волна определённой длины падает на плосковыпуклую линзу почти перпендикулярно. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе сред стекло-воздух, а волна 2 — в результате отражения от пластины на границе сред воздуха- стекло.

Если вторая волна запаздывает по сравнению с первой на целое число длин волн, то при сложении волны усиливают друг друга. Если вторая волна запаздывает по сравнению с первой на нечётное число полуволн, то колебания в точке сложения будут совпадать в противоположных фазах. При этом волны погасят друг друга.

В результате проделанного эксперимента Юнг смог получить картину, которая состоит из чередующихся параллельных полос (темных и светлых)

Интерференция света – это явление сложения двух и более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующегося максимумом и минимумом интенсивности.

Это интересно! Измеряя радиусы колец Ньютона, можно вычислить длины волн. В ходе измерений было установлено, что для красного света λ_кр = 8∙10 –7 м, а для фиолетового — λ_a = 4∙ 10 –7 м.

Пример №1. Будет ли наблюдаться интерференционная картина при освещении мыльной пленки монохроматическим светом? Какой она будет?

Поскольку источник света один и тот же, то отраженные от обеих поверхностей мыльной пленки волны будут когерентными. Поэтому интерференционная картина наблюдаться будет. Она примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

На поверхность тонкой прозрачной плёнки падает по нормали пучок белого света. В отражённом свете плёнка окрашена в зелёный цвет. При использовании плёнки такой же толщины, но с несколько меньшим показателем преломления, её окраска будет

а) только зелёной

б) находиться ближе к красной области спектра

в) находиться ближе к синей области спектра

Видео:11 класс, 16 урок, Интерференция и дифракция светаСкачать

Лекция № 22. Волновая оптика

Лекция № 22. Волновая оптика

1.Интерференция света. Условия образования интерференционного максимума и минимума.

2. Дифракция света. Принцип Гюйгенса. Метод зон Френеля.

3. Дифракция Фраунгофера в параллельных лучах. Дифракционная решётка.

4. Поляризации света при отражении и преломлении света. Двойное лучепреломление

Интерференция света. Условия образования

интерференционного максимума и минимума

Интерференция света – пространственное перераспределение светового потока при наложении двух (или нескольких) когерентных световых волн, в результате чего в одних местах возникают максимумы, в других – минимумы интенсивности. Когерентность – согласованное протекание во времени и пространстве колебательных процессов. Этому условию удовлетворяют монохроматические волны – волны постоянной частоты.

Для описания световой волны можно воспользоваться уравнением гармонических колебаний , где под понимают напряженность электрического или магнитного полей волны. И тогда интерференцию света можно объяснить рассматривая сложение колебаний. Для двух гармонических колебаний одного периода, происходящих по одному направлению, результирующая амплитуда А и интенсивность волны I (при I

и . (22.1)

Отсюда следует, что в тех точках пространства где , то , а там где , то . В частности, при будем иметь при , …2pm и при … (2m+1)p.

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдается интерференционная картина.

Анализ хода лучей от двух когерентных источников (Рис. 22.1) позволяет установить связь между возникшей разностью фаз в точке М и оптической разностью хода . При распространении лучей в однородной среде показатели преломления , а например, в воздухе принимают . Тогда

Если оптическая разность хода равна целому числу длин волн в вакууме

(), (22.2)

т. е. колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе. Следовательно (22.2) является условием интерференционного максимума. Если

, (), (22.3)

т. е. колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе. Следовательно (22.3) является условием интерференционного минимума.

Условия максимумов и минимумов при интерференции света, отражённого от верхней и нижней поверхностей тонкой плоскопараллельной плёнки (рис. 22.2), находящейся в воздухе () могут быть вычислены соответственно по выражениям:

Существуют различные способы наблюдения двухлучевой интерференции света на экране, осуществляемой делением волнового фронта и в которых создаётся оптическая разность хода : от двух щелей в опыте Юнга (рис. 22.3), от зеркал и бипризмы Френеля (рис. 22.4), от зеркала Ллойда и т. п.

Полосы равного наклона (интерференция от плоскопараллельной пластинки) – интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами. Они локализованы в бесконечности. Для наблюдения полос равного наклона используют собирающую линзу и экран Э, расположенный в локальной плоскости линзы. Параллельные лучи и соберутся в фокусе линзы (на рис. 22.5 её оптическая ось параллельна лучам и ), в эту же точку придут и другие лучи (луч ), параллельный лучу 1, в результате чего увеличивается общая интенсивность. Лучи 3, наклонённые под другим углом, соберутся в точке фокальной плоскости линзы. Если оптическая ось линзы перпендикулярна поверхности пластинки, то полосы равного наклона имеют вид концентрических колец с центром в фокусе линзы.

Полосы равной толщины (интерференция от пластинки переменной толщины) – интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины. Они локализованы вблизи поверхности клина. Каждая из полос возникает при отражении от мест пластинки, имеющих одинаковую толщину. В общем случае толщина пластинки может изменяться произвольно (на рис. 22.6 выбран клин, угол между боковыми гранями очень мал).

Кольца Ньютона – пример полос равной толщины. Они наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис. 22.7).

Радиусы светлых колец Ньютона в отражённом свете (или тёмных в проходящем свете)

, ,

где номер кольца, радиус кривизны линзы.

Радиусы тёмных колец Ньютона в отражённом свете (или светлых в проходящем свете)

, ,

Просветление оптики состоит в том, что на поверхность линзы наносится тонкая плёнка с показателем преломления меньшим, чем у материала линзы. Если оптическая толщина плёнки удовлетворяет условию , то отражённые лучи от линзы и от плёнки дают интерференционный минимум. А это, в свою очередь, приводит к увеличению интенсивности света, проходящего сквозь линзу без потерь.

Дифракция света. Принцип Гюйгенса – Френеля. Метод зон Френеля

Дифракция — совокупность явлений, наблюдаемых при распространении света в среде вблизи непрозрачных тел, сквозь малые отверстия и т. д. и связанных с отклонениями от геометрической оптики.

Распространение волн объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задаёт положение волнового фронта в следующий момент времени. Френель дополнил принцип Гюйгенса физическим содержанием, добавив в него идею об интерференции вторичных волн, создаваемых фиктивными источниками. Согласно принципу Гюйгенса – Френеля, световая волна, возбуждаемая каким-либо источником, может быть представлена как результат суперпозиции вторичных волн, излучаемых когерентными фиктивными источниками.

Френелем был предложен более простой способ нахождения амплитуды результирующих колебаний для симметричных случаев дифракции, когда размер отверстия значительно больше длины волны. Применим этот метод к дифракции сферической волны на круглой диафрагме (или преграждающем непрозрачном диске).

Световая волна от точечного источника S (рис. 22.8) в однородной изотропной среде имеет сферическую волновую поверхность. Разобьем ее на кольцевые зоны так, чтобы расстояния от границ зон до точки наблюдения P отличались на . Следовательно,

,

где – номер зоны Френеля; — расстояние от фронта волны до точки наблюдения P. Это приводит образованию зон одинаковой площади,

(22.4)

т. е. содержащих равновеликое количество когерентных источников колебаний, а в соседних зонах совершающих колебания в противофазе.

Радиус внешней границы й зоны Френеля для сферической волны

(22.5)

С учетом фазовых соотношений амплитуда волны в точке P может быть записана в виде ряда амплитуд колебаний, создаваемых зонами Френеля то есть

(22.6)

где с учетом примерного равенства амплитуд колебаний, создаваемых соседними зонами, проведена группировка, показывающая, что . Амплитуда колебаний E, создаваемых в точке P сферической волной, в половину меньше амплитуды, создаваемой первой зоной Френеля. Поэтому, если оставить открытой только первую зону, интенсивность света возрастет в 4 раза. Если отверстие в экране оставляет открытым чётное число зон, то в центре дифракционной картины получается тёмное пятно, при нечётном числе зон – светлое.

В центре тени от круглого экрана, закрывающего не слишком большое число зон Френеля, получается светлое пятно — пятно Пуассона.

Результаты теории Френеля послужили решающим доказательством волновой природы света и дали основу теории зонных пластинок, представляющих в простейшем случае стеклянные пластинки с системой чередующихся прозрачных и непрозрачных колец, построенных по принципу расположения зон Френеля.

Дифракция Фраунгофера в параллельных лучах.

Большое практическое значение имеет дифракция в параллельных лучах. Она наблюдается в том случае, если источник света и точка наблюдения бесконечно удалены от щели, вызывающего дифракцию. Чтобы реально осуществить данный вид дифракции достаточно источник света поместить в фокусе собирающей линзы, а дифракционную картину наблюдать в фокальной плоскости второй собирающей линзы, установленной за щелью.

Пусть плоская монохроматическая волна падает нормально на щель шириной . Оптическая разность хода лучей, идущих от краёв щели (рис. 22.9) в произвольном направлении будет

. (22.7)

Разобьём щель на зоны Френеля, имеющие вид полос, параллельных ребру щели. Ширина зон выбирается так, чтобы разность хода лучей от краёв соседних зон была равна . Тогда на ширине щели будет укладываться число зон, равное , т. е.

(22.8)

Амплитуды колебаний вторичных волн в плоскости щели будут одинаковы, так как выбранные зоны Френеля, имеют одинаковую площадь и одинаково наклонены к направлению наблюдения.

Из полученного выражения (22.8) следует, что число зон Френеля, укладывающихся на ширине щели, зависит от угла , а от числа зон, в свою очередь, зависит результат интерференции вторичных волн. Очевидно, что при чётном числе зон Френеля амплитуда результирующего колебания будет равна нулю, так как колебания от соседних зон будут гасить друг друга, и в данном направлении будет наблюдаться дифракционный минимум. Таким образом, условие дифракционного минимума будет иметь вид

(22.9)

Дифракционный максимум при выполнении условия

(22.10)

Таким образом, положение дифракционных максимумов и минимумов зависит от длины волны монохроматического излучения. При освещении щели белым светом будет наблюдаться радужное окрашивание полос на экране в точке В (рис. 22.9) обращённого фиолетовым цветом в сторону к центральному максимуму, точка В0, хотя сам максимум имеет вид белой полоски.

На рисунке 22.10 показано распределение интенсивности света на экране в зависимости от угла .

Для анализа спектров излучения возбуждённых атомов используются дифракционные решётки. У прозрачных дифракционных решеток штрихи наносятся на поверхность прозрачной (обычно стеклянной пластинки) (или вырезаются в виде узких щелей в непрозрачном экране). Если ширина щели равна , а ширина непрозрачного участка , то величину называют периодом (постоянной) дифракционной решетки (рис. 22.11).

Дифракционная картина на решётке определяется как результат взаимной интерференции волн, идущих от всех щелей, т. е. в дифракционной решётке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей. Поэтому условие главных максимумов дифракционной решётки, на которую свет падает нормально

, (22.11)

условие главных минимумов решётки

. (22.12)

Условие дополнительных минимумов дифракционной решётки, на которую свет падает нормально:

, (22.13)

где период дифракционной решётки; число штрихов решётки; кроме

При освещении решетки белым светом все максимумы, кроме центрального, разлагаются в спектр, фиолетовый конец которого расположен ближе к центру дифракционной картины, красный – наружу.

Основными характеристиками дифракционной решётки являются дисперсия и разрешающая сила. Дисперсия определяет угловое расстояние между двумя спектральными линиями, отличающимися, по длине волны на единицу. Разрешающая сила определяет минимальную разность длин волн , при которой две линии воспринимаются в спектре раздельно: и

На рисунке 22.10 показано распределение интенсивности света на экране в зависимости от угла для дифракционной решётки.

Поляризации света при отражении и преломлении света.

Свет представляет собой поперечные электромагнитные волны, в которых векторы колеблются во взаимно перпендикулярных направлениях и перпендикулярны вектору скорости распространения волны . Поэтому для полного описания состояния поляризации светового пучка достаточно знать поведение одного из этих векторов. Обычно рассматривается поведение вектора Е (световой вектор). Это связано с тем, что взаимодействие света с веществом обусловлено именно электрической составляющей электромагнитной волны. Плоскость, в которой колеблется световой вектор, называется плоскостью поляризации.

Световая волна, излучаемая источником, представляет собой излучение огромного числа атомов, каждый из которых излучает свет независимо от других атомов. Поэтому в световой волне присутствуют колебания всевозможных направлений. Свет со всевозможными и равновероятными направлениями колебаний светового вектора получил название естественного света.

Свет, в котором колебания светового вектора, каким либо образом упорядочены (в результате внешнего воздействия) называется поляризованным.

Если колебания светового вектора происходят в одной плоскости, то такой свет называется плоско поляризованным.

За меру поляризации света принимается величина называемая степенью поляризации

, (22.12)

где — интенсивность колебания в двух взаимно перпендикулярных направлениях. В частности для естественного света Р = 0, так как , а для плоско поляризованного света Р = 1, так как .

Естественный свет можно преобразовать в плоско поляризованный, используя для этого так называемые поляризаторы, пропускающие колебания только одного направления, например, кристаллы турмалина.

Если на пути светового луча поставить пластинку, определенным образом вырезанную из кристалла турмалина, то при вращении пластинки вокруг направления распространения луча, не наблюдаются ни каких изменений в интенсивности луча, прошедшего через пластинку. Таким образом, световая волна, падающая на турмалин от обычного источника, не обнаруживает асимметрии по отношению к направлению распространения. Иначе будет обстоять дело, если на пути луча, вышедшего из первой пластинки установить вторую такую же пластинку (рис. 22.11). В зависимости от того, как ориентированы эти пластинки интенсивность света, вышедшего из второй пластинки, меняется от максимальной (пластинки параллельны) до нуля (полное гашение) (пластинки взаимно перпендикулярны). Малюс на опыте установил, что интенсивность света, прошедшего вторую пластинку изменяется по закону

, (22.13)

где — интенсивность света, падающего на вторую пластинку.

Результаты этого опыта можно объяснить следующим образом. Первая пластинка, пропуская свет только одного направления, преобразует естественный свет в плоско поляризованный и поэтому называется поляризатором. Вторая пластинка служит для определения степени поляризации света и называется анализатором. Если оптические оси поляризатора и анализатора параллельны, то свет проходит через анализатор без изменения. Если оптическая ось анализатора перпендикулярна оптической оси поляризатора, то анализатор не пропускает колебаний и интенсивность света, проходящего через вторую пластинку, будет равна нулю.

Если естественный свет с интенсивностью пропустить через две пластинки, то интенсивность света, вышедшего из первой пластинки и падающее на вторую пластинку будет , и тогда закон Малюса будет иметь вид

. (22.14)

При падении света на границу раздела двух диэлектриков (рис.22.12) наблюдается явление отражения и преломления света. Если на пути отраженного и преломленного лучей поместить анализатор, то можно убедиться в том, что эти лучи частично поляризованы. При этом в отраженном луче преобладают колебания перпендикулярные плоскости падения луча, в преломленном луче – колебания параллельные плоскости падения луча. Степень поляризации лучей зависит от угла падения луча. Как показал Брюстер, при угле падения удовлетворяющем условию

(22.15)

отраженный луч полностью поляризован, а преломленный луч, максимально поляризован. При этом отраженный и преломленный лучи взаимно перпендикулярны.

Явление двойного лучепреломления было обнаружено Бартолином на кристаллах исландского шпата. Кристаллы турмалина встречаются в естественном состоянии в виде довольно больших и оптически чистых образцов и, поэтому до настоящего времени исландский шпат является наилучшим материалом для изготовления оптических приборов, использующих поляризацию света.

Если на толстый кристалл исландского шпата направить луч света, то из кристалла выйдут два пространственно разделенных луча (рис. 22.13), даже в том случае, если угол падения равен нулю. Один из этих лучей является продолжением падающего, и поэтому получил название обыкновенного, «о», а второй отклоняется, и поэтому получил название необыкновенного, «е». При вращении кристалла вокруг направления падающего луча, то один из преломленных лучей (обыкновенный) будет неподвижным, а второй (необыкновенный) будет вращаться вокруг первого. Различие в отклонении обоих лучей показывает, что они обладают различными показателями преломления. При исследовании явления двойного лучепреломления было установлено, что обыкновенный луч имеет один и тот же показатель преломления для всех направлений, а показатель преломления необыкновенного луча зависит от направления в кристалле.

Если исследовать оба луча с помощью анализатора, то можно обнаружить, что оба луча поляризованы, и притом во взаимно перпендикулярных направлениях.

Двойное лучепреломление может наблюдается при возникновении искусственной оптической анизотропии в средах под действием механической деформации, электрического (эффект Керра) или магнитного поля.

Оптически активные среды, обладают способностью вращать плоскость поляризации при прохождении света через твёрдые тела или жидкие растворы.

🎦 Видео

ИнтерференцияСкачать

Дифракция света ● 1Скачать

Дифракция света. Дифракционные решетки. 11 класс.Скачать

Урок 416. Интерференция в тонких пленкахСкачать

Интерференция светаСкачать

Как узнать интерференцию?Скачать

Дифракция Фраунгофера. Дифракция на щели. Лекция 14-1Скачать

Интерференция светаСкачать

Интерференция и Дифракция света. ЕГЭ Физика. Николай НьютонСкачать

Конструктивная и деструктивная интерференция (видео 3) | Интерференция волн | ФизикаСкачать

ИЗУЧЕНИЕ ДИФРАКЦИИ И ИНТЕРФЕРЕНЦИИ УЛЬТРАЗВУКА В ОДНО- И МНОГОЩЕЛЕВЫХ СИСТЕМАХСкачать