Магнитное поле порождает вихревое поле уравнение (4 видео)

Содержание

Уравнения Максвелла Вихревое электрическое поле
Вихревой характер магнитного поля
Вихревое магнитное поле
Различие между потенциальными и вихревыми полями
Вихревое электрическое поле
Электромагнитная индукция
Вихревое электрическое поле
Ток смещения и электромагнитная волна
Что мы узнали?
💥 Видео

Видео:Электродинамика | вихревое электрическое полеСкачать

Уравнения Максвелла Вихревое электрическое поле

Вихревое электрическое поле

Из закона Фарадея следует: любое изменение сцепленного с контуром потока магнитной индукции приводит к возникновению электродвижущей силы индукции и вследствие этого появляется индукционный ток.

Следовательно, возникновение ЭДС электромагнитной индукции возможно и в неподвижном контуре, находящемся в переменном магнитном поле. Но ЭДС в любой цепи возникает только когда в ней на носители тока действуют сторонние силы – силы неэлектростатического происхождения.

Из опытов следует, что сторонние силы не связаны с тепловыми и химическими процессами в контуре. Их возникновение также нельзя объяснить силами Лоренца, так как они не действуют на неподвижные заряды.

Максвелл выдвинул гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре.

По Максвеллу, контур, в котором появляется ЭДС, играет второстепенную роль, являясь своего рода «прибором» для обнаружения этого поля.

Изменяющееся во времени магнитное поле порождает электрическое поле, циркуляция которого:

— проекция вектора на направление .

– магнитный поток

Если поверхность и контур неподвижны, то

Из электростатики: циркуляция вектора напряженности электростатического поля вдоль замкнутого контура равна 0:

Сравнивая последние формулы, получим принципиальное различие: циркуляция вектора по сравнению с циркуляцией не равна нулю. Следовательно, электрическое поле, возбуждаемое магнитным полем, как и само магнитное поле, является вихревым.

Если любое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: любое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля.

Для установления количественных отношений между ними Максвелл ввел понятие тока смещения.

Рассмотрим цепь переменного тока, содержащую конденсатор.

Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор протекают токи смещения в тех местах, где отсутствуют проводники.

По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток смещения, равный току в подводящих проводах. То есть токи смещения и токам проводимости:

Ток проводимости вблизи обкладок конденсатора:

Поверхностная плотность заряда у на обкладках равна электрическому смещению D в конденсаторе.

Для общего случая можно записать:

Сравнивая это выражение с выражением для силы тока:

— плотность тока смещения.

Направления вектора , вектора совпадают с направлением вектора .

Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространстве магнитное поле.

В диэлектриках ток смещения состоит из двух слагаемых:

— плотность тока смещения

— плотность тока поляризации – тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике (смещение зарядов в неполярных молекулах или поворот диполей в полярных молекулах).

Возбуждение магнитного поля токами поляризации правомерно, так как токи поляризации по своей природе не отличаются от токов проводимости.

Название «ток смещения» является условным (исторически сложившимся). По своей сути – это изменяющееся во времени электрическое поле. Поэтому ток смещения существует не только в вакууме или диэлектриках, но и внутри проводников, по которым течет переменный ток, однако он пренебрежимо мал по сравнению с током проводимости. Наличие тока смещения подтверждено экспериментально .

Максвелл ввел понятие полного тока, равного сумме токов проводимости и смещения.

Плотность полного тока:

Полный ток в цепи переменного тока всегда замкнут, то есть на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника есть ток смещения, который замыкает ток проводимости.

Максвелл обобщил теорему о циркуляции, введя в ее правую часть полный ток:

— обобщенная теорема о циркуляции вектора Н.

В основе теории Максвелла лежат 4 уравнения:

— обобщенная теорема о циркуляции вектора

Магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями

– электрическое поле может быть как потенциальным, так и вихревым. Источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля. — теорема Гаусса для поля .

Источниками электрического поля являются электрические заряды. Линии напряженности направлены от положительного заряда к отрицательному.

— теорема Гаусса для поля .

природе не существуют магнитные заряды. Линии магнитной индукции замкнуты.

Третье уравнение – следствие первого, четвертое уравнение – следствие второго.

Переменный во времени электрический ток в соответствии с уравнением 1 создает переменное во времени вихревое магнитное поле. В соответствии с уравнением 2, возникающее переменное магнитное поле создает переменное вихревое электрическое поле. Возникшее переменное поле уже независимо от наличия тока создает переменное магнитное поле. И так далее до бесконечности.

Величины, входящие в уравнения Максвелла не являются независимыми. Существующую между ними связь отражают материальные уравнения.

, ,

G – удельная проводимость вещества.

Уравнения Максвелла не симметричны относительно электрических и магнитных полей, так как в природе существуют электрические заряды, а магнитных зарядов нет.

Дифференциальная форма уравнений Максвелла:

Если заряды распределены в пространстве непрерывно, то интегральная и дифференциальная формы уравнений эквивалентны. Если есть поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма является более общей. Чтобы достигнуть математической эквивалентности, уравнения дополняются граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред.

, , ,

Видео:Урок 283. Вихревое электрическое полеСкачать

Вихревой характер магнитного поля

Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.

Электростатические поля имеют силовые линии, начинающиеся и заканчивающиеся на электрических зарядах, причем, всегда находятся в разомкнутом состоянии. Линии магнитного поля замкнуты. Это говорит об отсутствии магнитных зарядов в природе.

Электрический ток образуется благодаря движению электрических зарядов. Так как магнитных зарядов нет, это объясняет отсутствие магнитного тока. Данное утверждение можно выразить при помощи уравнения:

Определение вихревого поля также выполнимо другим способом.

Видео:Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Вихревое магнитное поле

Векторные поля, вектор которых не равен нулю – это вихревые магнитные поля.

Следуя из теоремы о циркуляции локального вида, которая влияет на вихревой характер магнитного поля:

r o t B → = μ 0 j → ( 2 ) , где j → считается объемной плотностью тока, и второй формы определения вихревого поля можно заключить, что магнитное поле будет вихревым там, где проходят токи, а безвихревым там, где их нет.

При отсутствии токов вектор магнитной индукции B → представляется в виде градиента скалярного магнитного потенциала φ m :

B → = — g r a d φ m ( 3 ) .

Если имеются токи, то данное представление невозможно.

Видео:Уравнения Максвелла. Вихревое электрическое поле. Ток смещенияСкачать

Различие между потенциальными и вихревыми полями

Основными уравнениями магнитного поля постоянных токов считаются выражения вида:

r o t B → = μ 0 j → d i v B → = 0 ( 4 ) .

Произведем сравнение с основными уравнениями электростатики:

r o t E → = 0 d i v E → = 1 ε 0 ρ ( 5 ) .

Рассматривая систему ( 5 ) , видно, что электрическое поле всегда потенциально, а его источниками являются электростатические (неподвижные) заряды.

Магнитное поле считается вихревым при наличии токов. Оно зависит от формы контура и не определяется только положением начала и конца этого контура. Существование однозначной разности потенциалов в магнитном поле исключено. Значение магнитного напряжения по замкнутому контуру не равняется нулю.

Электрические токи являются источниками поля. Магнитное поле считается вихревым, так как его дивергенция везде равна нулю. Его также называют соленоидальным. Определение потенциального электростатического поля возможно при заданной дивергенции напряженности d i v E → ( x , y , z ) в качестве функции координат. Полное определение вихревого магнитного поля реально, когда имеется мощность его вихрей, то есть r o t B → ( x , y , z ) как функция координат.

Показать, почему для вихревого магнитного поля нельзя представить вектор индукции B → в виде градиента магнитного потенциала φ m .

B → = — g r a d φ m ( 1 . 1 ) .

Для выражения ( 1 . 1 ) можно применить операцию r o t :

r o t B → = — r o t g r a d φ m ( 1 . 2 ) .

Известно значение r o t :

r o t ( g r a d φ m ) = 0 ( 1 . 3 ) .

При подстановке ( 1 . 3 ) в ( 1 . 2 ) имеем:

Ответ: Вспомнив теорему о циркуляции, получаем отсутствие токов. В данном случае, представление вектора индукции магнитного поля невозможно в виде магнитного потенциала в области, где проходят токи.

Применение понятия скалярного магнитного потенциала φ m возможно только в области пространства, где j → = 0 . Данная часть пространства φ m характеризуется неоднозначностью функции. Показать это.

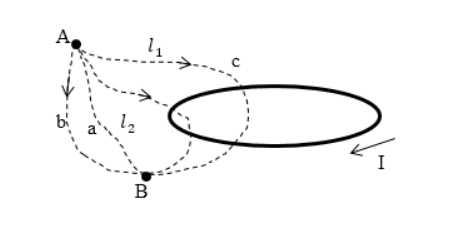
Необходимо рассмотреть магнитное поле возле контура с током, как изображено на рисунке 1 . По теореме о циркуляции для любого контура выполнимо равенство:

Если токов нет, магнитное поле становится потенциальным, интеграл, который необходимо взять между A и B , не зависит от пути интегрирования, то запись примет вид:

∫ A a B B → d l → = ∫ A b B B → d l → ( 2 . 2 ) .

∫ A b B B → d l → = ∫ A B B → d l → = φ m A — φ m B ( 2 . 3 ) .

Выражение ( 2 . 3 ) может быть рассмотрено в качестве разности скалярных магнитных потенциалов в точках A и B . Можно пойти иным путем и принять значение потенциала равным нулю в точке В , как выполнялось для нахождения потенциала в электростатике:

∫ A B B → d l → = φ m A ( 2 . 4 ) .

При выборе контура, охватывающего какой-либо ток (контур A c b B ), как показано на рисунке 1 , линейный интеграл по замкнутому контуру от циркуляции вектора индукции по нему будет не равен нулю:

∮ A c b B B → d l → ≠ 0 ( 2 . 5 ) .

∮ A c b B B → d l → ≠ ∫ A c B B → d l → — ∫ A b B B → d l → = I ≠ 0 ( 2 . 6 )

∫ A c B B → d l → = ∫ A b B B → d l → + I = φ m A — φ m B + I ( 2 . 7 ) .

При выборе какого-либо пути A n B , охватывающего ток в количестве n раз, имеем:

∫ A n B B → d l → = φ m A — φ m B + n I ( 2 . 8 ) .

Следует задать нулевой потенциал в точке В :

∫ A n B B → d l → = φ m A + n I ( 2 . 9 ) .

Ответ: Получив уравнение ( 2 . 9 ) , очевидно, что скалярный магнитный потенциал является неоднозначной величиной.

Видео:Вихревое электрическое полеСкачать

Вихревое электрическое поле

Средняя оценка: 4.5

Всего получено оценок: 247.

Средняя оценка: 4.5

Всего получено оценок: 247.

Одним из следствий уравнений электродинамики Максвелла является существование электрического поля, не имеющего источников — зарядов. Такое электрическое поле называется вихревым. Поговорим кратко о вихревом электрическом поле.

Видео:Электромагнитное поле | Физика 9 класс #43 | ИнфоурокСкачать

Электромагнитная индукция

Согласно закону электромагнитной индукции, при изменении магнитного потока через замкнутый контур в нем наводится ЭДС индукции. Его формула:

Каков механизм возникновения ЭДС в контуре?

Возникновение ЭДС означает, что в контуре появляются силы, которые перемещают свободные носители заряда в веществе контура. Магнитное поле, пронизывающее контур, не взаимодействует с носителями: оно не влияет на покоящиеся заряды. Таким образом, единственные силы, которые могут перемещать заряды в нём, — это силы электрического поля.

Следовательно, при изменении магнитного поля в контуре появляется электрическое поле, которое перемещает заряды и создает ЭДС индукции.

Рис. 1. Электромагнитная индукция.

Видео:60. Уравнения МаксвеллаСкачать

Вихревое электрическое поле

Однако поле, возникающее в контуре, имеет важное отличие от электрического поля, порождаемого зарядами (статического электрического поля). Силовые линии статического поля начинаются и заканчиваются на зарядах, но в данном случае зарядов нет, а значит, и линии образующегося электрического поля не имеют начала и конца — они замкнуты.

Поле с замкнутыми силовыми линиями называется вихревым. Например, все существующие магнитные поля — вихревые. Теория не запрещает существование статического магнитного поля, однако магнитные заряды пока не обнаружены. Точно таким же вихревым является поле, возникающее в контуре при изменении магнитного потока через контур.

Суть механизма электромагнитной индукции состоит в том, что изменение магнитного поля порождает вихревое электрическое поле, которое и приводит заряды в контуре в движение, создавая ЭДС индукции.

Чем быстрее меняется поток через контур, тем больше напряженность порождаемого им электрического поля. Направление электрического поля совпадает с направлением индукционного тока в контуре, а значит, оно также определяется правилом Ленца: индукционный ток, возникающий в замкнутом контуре, направлен так, чтобы противодействовать причине, его вызывающей.

При увеличении магнитного потока через контур, направление вихревого электрического поля может быть определено правилом обхвата правой рукой: если большой палец правой руки указывает на направление магнитного поля, то четыре охватывающих пальца укажут направление вихревого электрического поля. При уменьшении магнитного потока направление вихревого поля поменяется на противоположное.

Видео:Вихревое электрическое полеСкачать

Ток смещения и электромагнитная волна

Поскольку вихревое магнитное поле порождается током, текущим по проводнику, Дж. Максвелл при разработке теории электромагнетизма предположил, что вихревое электрическое поле также порождается аналогичным процессом, который был назван током смещения (в отличие от обычного тока проводимости). Подобно тому, как ток проводимости является «движением» электрического поля, ток смещения может рассматриваться как «движение» магнитного поля. Именно ток смещения порождает вихревое электрическое поле. А электрическое поле, в свою очередь создавая обычный электрический ток, порождает вихревое магнитное поле.

В итоге при изменении электрического и магнитного поля в пространстве сразу же образуется распространяющаяся структура взаимопорождающих магнитных и электрических полей, называемая электромагнитной волной.

Рис. 3. Электромагнитная волна.

Видео:вихревое E - поле. 18.06.20.Скачать

Что мы узнали?

Изменение магнитного потока через контур вызывает в нем возникновение вихревого электрического поля. Именно это вихревое поле является источником ЭДС электромагнитной индукции. Для определения его направления используется правило Ленца.