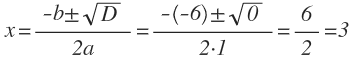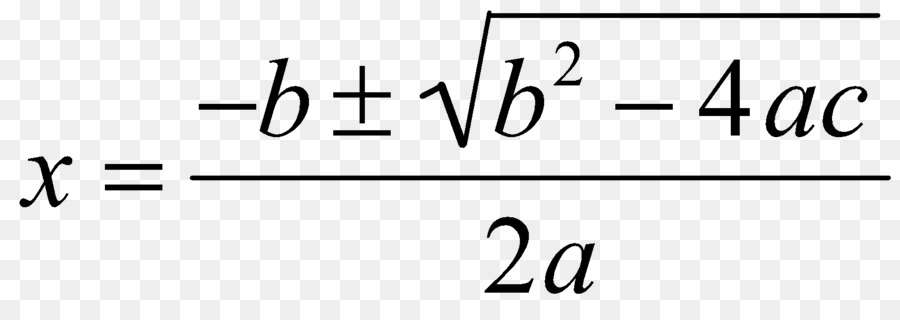Любые уравнения с дискриминантом решения

О чем эта статья:

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Видео:Как решать квадратные уравнения через дискриминант. Простое объяснениеСкачать

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Видео:Решение квадратных уравнений. Дискриминант. Практическая часть. 1ч. 8 класс.Скачать

Дискриминант: примеры решения уравнений

Существуют несколько способов решения уравнений квадратных, однако использование формулы, которая связывает коэффициенты равенств названного типа, является универсальным. Этот способ часто называют методом «через дискриминант». Примеры решения уравнений квадратных с помощью него приводятся в данной статье. О них должен знать каждый старшеклассник.

Видео:КВАДРАТНОЕ УРАВНЕНИЕ дискриминантСкачать

Квадратные уравнения

Примеры с дискриминантом относятся к решению уравнений квадратных. Такие уравнения имеют вид, представленный на фото ниже.

Вам будет интересно: Диагностика Стребелевой: описание метода, применение, особенности, отзывы

Здесь a, b и c — это некоторые коэффициенты (числа), которые называются квадратичным, линейным и свободным членом, соответственно. Если известны значения икса такие, при которых равенство на фото является истиной, тогда говорят о том, что они являются корнями этого уравнения.

Как можно заметить, это уравнение называется квадратным, потому что «2» является максимальной степенью, в которую возводится x. Если a = 0, тогда уравнение превращается в линейное.

Вам будет интересно: Как правильно: Наталия или Наталья? Разбираемся вместе

Поскольку максимальная степень уравнения равна двум, то существовать могут только 0, 1 или 2 его корня, которые будут принимать действительные числовые значения.

Чтобы решить названное уравнение, можно воспользоваться несколькими методами. Тем не менее, самым простым и надежным из них является применение формулы с дискриминантом.

Видео:Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Какой формулой нужно пользоваться?

Формула метода решения уравнений квадратных через дискриминант записывается так, как представлено на рисунке ниже.

Можно видеть, что для ее использования необходимо знание всех трех коэффициентов уравнения, а знак «±», стоящий перед корнем, говорит о том, что формула позволяет находить одновременно два разных корня.

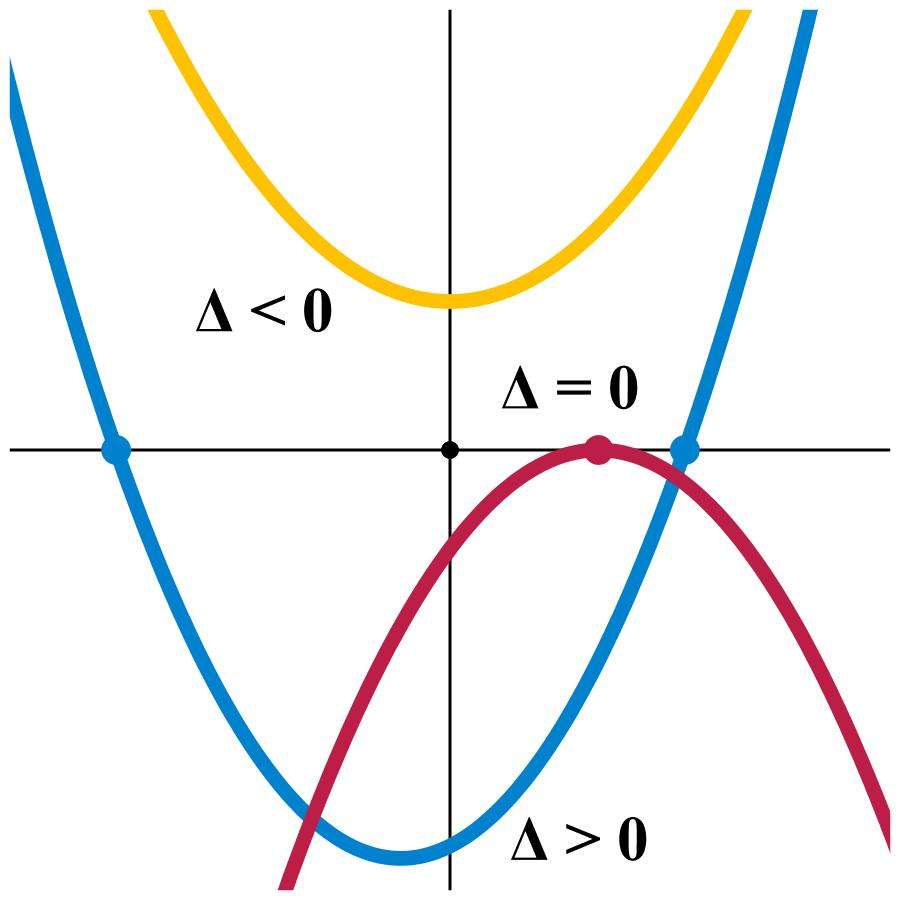
Подкоренное выражение называется дискриминантом. Он обычно обозначается латинской буквой D либо греческой Δ. Почему выделяют именно эту часть в представленной формуле? Дело в том, что от знака D зависит, сколько корней будет иметь соответствующее уравнение, и какими будут они.

Так, если D положительный, то выражение приводит к двум разным решениям уравнения квадратного, если же D отрицательный, тогда нет действительных чисел, которые бы удовлетворяли исходному равенству. В этом случае говорят о мнимых корнях, выраженных в виде комплексных чисел. Наконец, если D = 0, то формула приводит к существованию одного единственного корня.

Вам будет интересно: Эруковая кислота: где содержится, ее свойства и вред

Видео:Решение показательных неравенств шаг за шагомСкачать

Важные свойства корней в методе «через дискриминант»

Прежде чем перейти к рассмотрению конкретных примеров уравнений с дискриминантом, необходимо привести два важных свойства корней, полученных методом решения с использованием рассматриваемой формулы.

Первое свойство заключается в том, что их сумма (x1 + x2) равна отношению линейного коэффициента (b) к первому или квадратичному коэффициенту (a), взятое с обратным знаком, то есть -b/a.

Второе свойство состоит в том, что произведение x1 * x2 всегда равно отношению свободного члена (c) к первому коэффициенту (a), то есть c / a.

Приведенные равенства, которые связывают корни уравнения с его коэффициентами, составляют суть так называемой теоремы Виета.

Отметим, что эти формулы справедливы для любого уравнения квадратного (в том числе и неполного, то есть у которого b или/и c равен нулю).

Далее в статье рассмотрим использование формулы с дискриминантом уравнения квадратного в примерах, которые будут сформулированы в виде задач, имеющих практическое значение.

Видео:Алгебра 9 класс. 8 сентября. квадратные уравненияСкачать

Задача № 1. Произведение и сумма чисел

Первым примером уравнения с дискриминантом будет следующий: необходимо назвать два числа, сумма которых равна 34, а произведение 273.

Согласно условию задачи, составим систему уравнений, обозначив неизвестных два числа, как x1 и x2. Получаем:

Выразив x2 через x1 в первом уравнении, и подставив его во второе, имеем: (34 -x1) * x1 = 273. Раскрывая скобки, получим: (x1)2 — 34 * x1 + 273 = 0. То есть условие задачи свелось к решению уравнения квадратного.

Решаем этот пример формулой с дискриминантом: D = (-34)2 — 4 * 1 * 273 = 64. Получилось удобное для вычисления корня квадратного число. Решения этого уравнения будут иметь вид: x1 = (34 ± √64) / 2 = (21; 13). Каждое из полученных чисел x1 подставим в первое уравнение приведенной выше системы, получаем: x2 = (34 — 21 = 13; 34 — 13 = 21).

Таким образом, всего одна пара чисел (13 и 21) удовлетворяет условию задачи. Поскольку сумму мы уже проверили, то проверим теперь произведение: 13 * 21 = 273.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Задача №2. Составление и решение уравнения по заданному условию

В приведенном далее примере формула с дискриминантом также потребуется для его решения. Итак, условие формулируется следующим образом: найти число, двойной квадрат которого превосходит его на 45. Записываем языком математики это условие: 2 * x2 — x = 45. То есть снова задача сводится к нахождению неизвестного x в квадратном уравнении.

Перенесем все члены в левую часть равенства и вычислим дискриминант: D = 1 — 4 * 2 * (-45) = 361. Корень этого числа равен 19. Поэтому решениями уравнения будут числа: x = (1 ± 19) / (2 * 2) = (5; -4,5).

Проверим этот результат: 2 * 52 = 50, что действительно превосходит число 5 на 45; 2 * (-4,5)2 = 40,5, это число также удовлетворяет условию (40,5 — (-4,5) = 45).

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Задача №3. Определение сторон прямоугольного треугольника

Еще одним примером с дискриминантом квадратного уравнения является следующая задача: известно, что разность между двумя сторонами прямоугольника равна 70 см. Необходимо найти его стороны, если диагональ фигуры равна 130 см.

Условие задачи позволяет составить систему из двух уравнений:

Здесь x1 и x2 — неизвестные стороны прямоугольника. Поясним, откуда взялось второе уравнение. Поскольку диагональ прямоугольника образует с двумя его сторонами треугольник с углом 90o, то стороны его, которые равны x1 и x2, являются катетами, поэтому можно воспользоваться их связью с диагональю -гипотенузой (теорема Пифагора).

Выразив из первого уравнения x2, подставив его значение во второе уравнение, и раскрыв в нем скобки, получаем: 2 * (x1)2 — 140 * x1 — 12 000 = 0. Решаем это классическое уравнение квадратное: D = (140)2 — 4 * 2 * (-12 000) = 115600. Использование калькулятора позволяет рассчитать корень из этого числа, он равен 340. Корни этого уравнения равны: x1 = (140 ± 340) / 4 = (120; -50). Отрицательное число следует сразу отбросить, поскольку сторона прямоугольника — положительная величина.

Подставляя x1 = 120 см в первое уравнение системы, получаем, что x2 = 50 см.

Таким образом, неизвестные стороны прямоугольника равны 120 см и 50 см.

Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Задача №4. Два мотоциклиста

Следующий пример уравнения через дискриминант связан с решением задачи про двух мотоциклистов. Известно, что каждый из них выехал навстречу другому. Начальное расстояние между ними было равно 130 км, скорость одного составляла 30 км/ч, а другой ехал со скоростью на 33 км/ч больше, чем число часов, через которые они встретились. Необходимо найти, через какое время встретятся мотоциклисты.

Обозначим неизвестное время буквой t. Из условия задачи следует, что скорость второго мотоциклиста равнялась 33 + t. До встречи каждый мотоциклист проехал расстояние 30 * t и (33 + t) * t. Очевидно, что в момент встречи оба транспортных средства преодолели суммарное расстояние 130 км (см. условие задачи). Тогда получаем уравнение: 30 * t + (33 + t) * t = 130. Раскрывая скобки, получаем следующий вид: t2 + 63 * t — 130 = 0. Вычисляем в этом примере дискриминант: D = (63)2 -4 * 1 * (-130) = 4489. Корень из него будет равен 67. Значения t, удовлетворяющие уравнению, будут равны: t = (-63 ± 67) / 2 = (2; -65). Поскольку время не может быть отрицательным, получаем ответ на задачу: мотоциклисты встретятся через 2 часа.

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Задача №5. Аренда лодки группой молодых людей

Завершить эту статью хотелось бы примером и решением через дискриминант одной интересной задачи: несколько молодых людей решили арендовать лодку за 14 000 рублей. Они эту сумму поделили на всех. Однако в самый последний момент трое человек отказались плыть на лодке, поэтому каждый из оставшихся вынужден был доплатить еще 1500 рублей. Сколько человек хотели арендовать лодку изначально?

Пусть изначально было x молодых людей. Тогда каждый из них должен был заплатить сумму 14000 / x рублей. Как только трое человек отказались плыть, последняя сумма для каждого оставшегося стала равна 14000 / (x-3). Поскольку последняя сумма возросла по сравнению с первоначальной на одного человека на 1500 рублей, то можно составить такое уравнение: 14000 / (x-3) — 14000 / x = 1500.

Приведем это уравнение к квадратному. Имеем: 14000 * x — 14000 * x + 14000 * 3 = 1500 * x * (x-3). Раскрывая скобки и, упрощая выражение, получим: 1500 * x2 — 4500 * x — 42 000 = 0. Разделив обе части равенства на 1500, получим выражение: x2 — 3 * x — 28 = 0. Решаем этот пример дискриминантом: D = 9 — 4 * 1 * (-28) = 121. Тогда x = (3 ± 11) / 2 = (7; -4).

Таким образом, изначально группа молодых людей состояла из 7 человек.

Видео:Быстрый способ решения квадратного уравненияСкачать

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Если D>0, то уравнение имеет два различных

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Видео:Отрицательный дискриминантСкачать

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить

🎥 Видео

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать