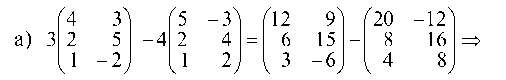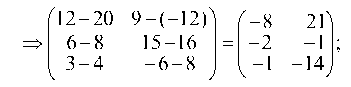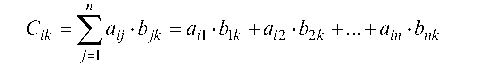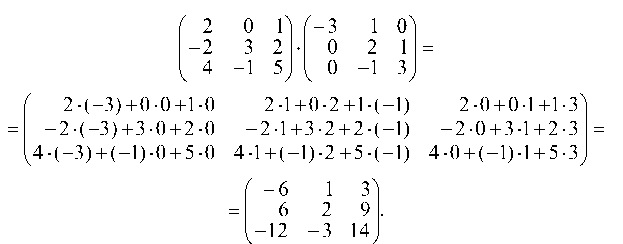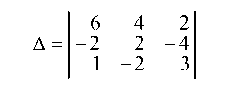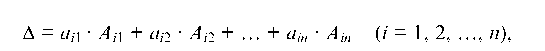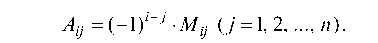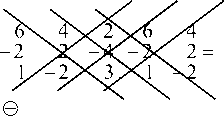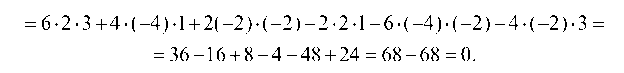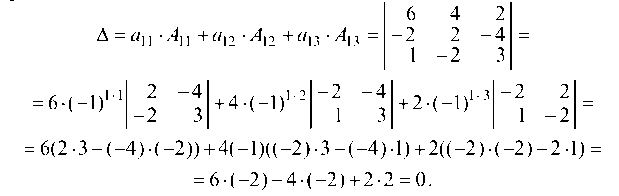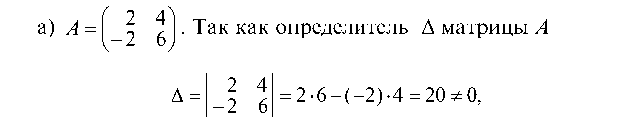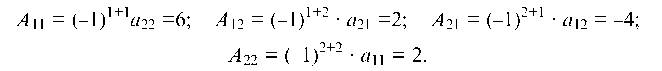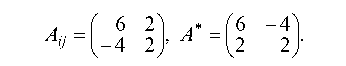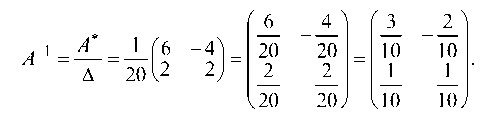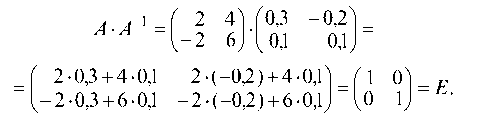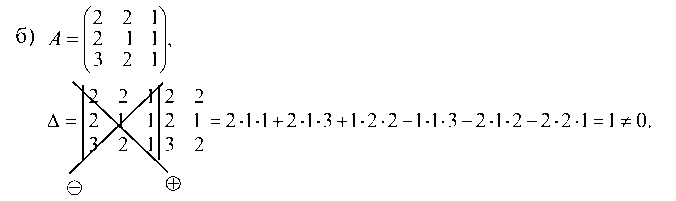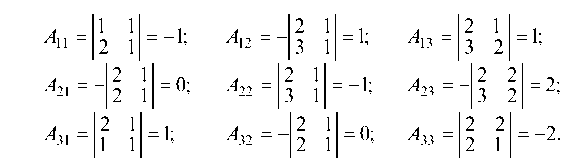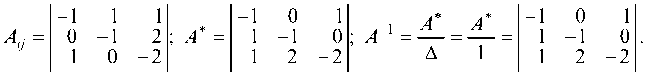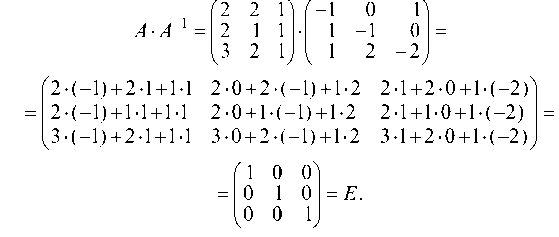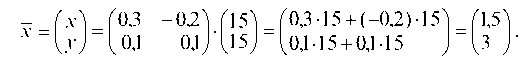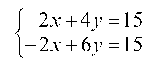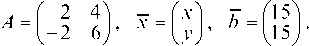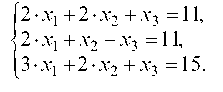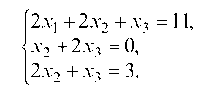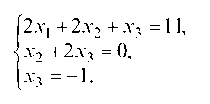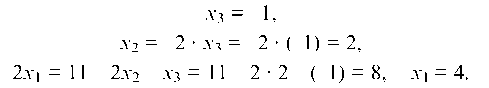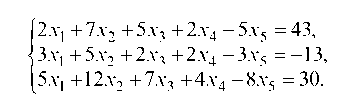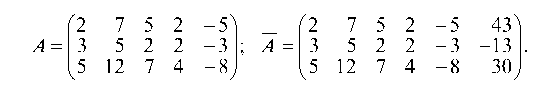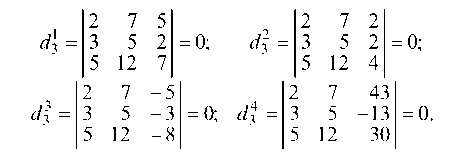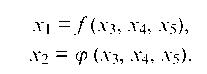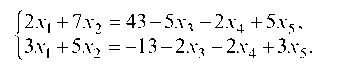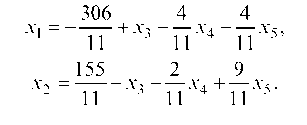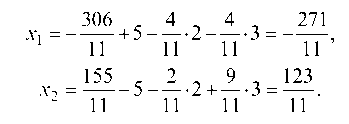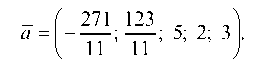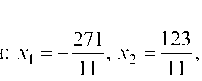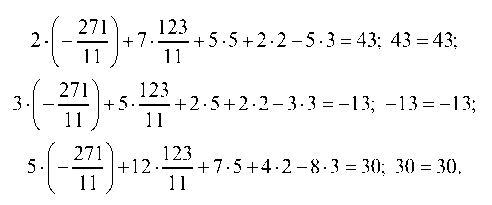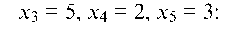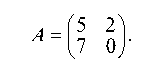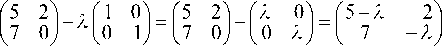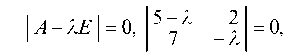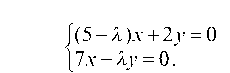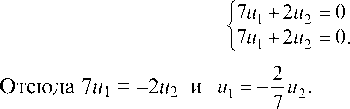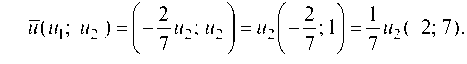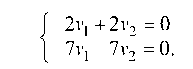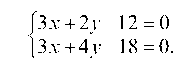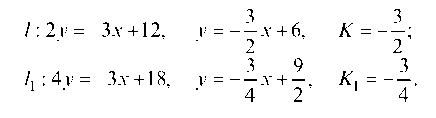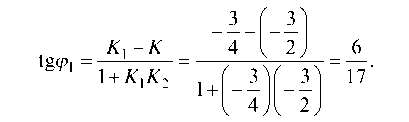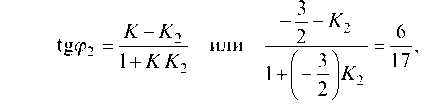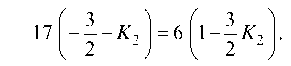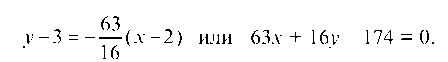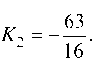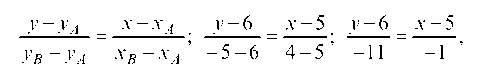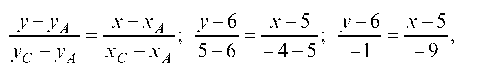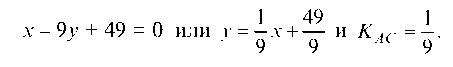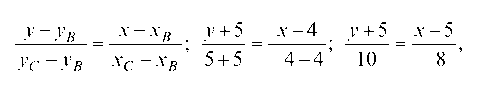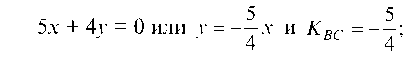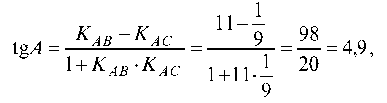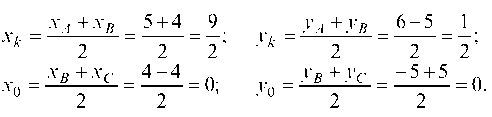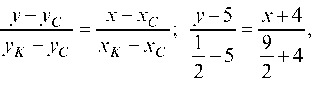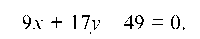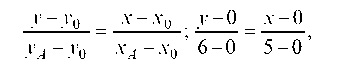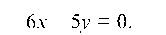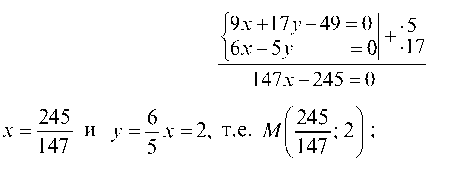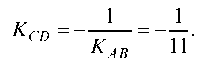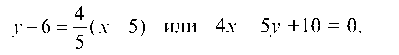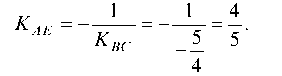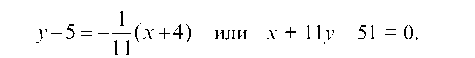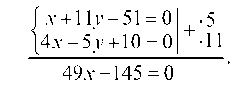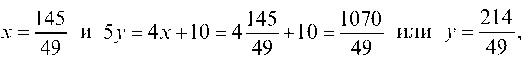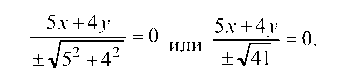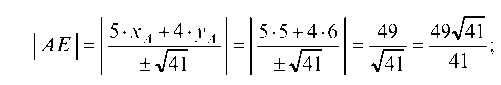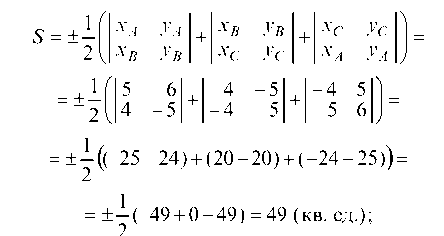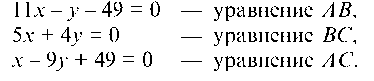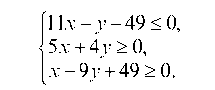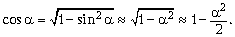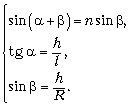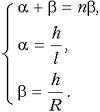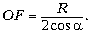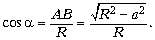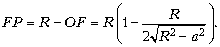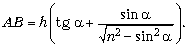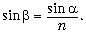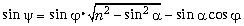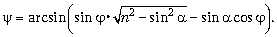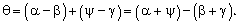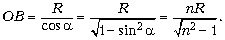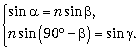Видео:Урок 199 (осн). Задачи на законы отраженияСкачать

Содержание
Вы уже ознакомились с уроками «Отражение света» и «Плоское зеркало«. На этих уроках мы рассматривали природу такого явления, как отражения света, и получение изображения в плоском зеркале.
На данном уроке вы познакомитесь с примерами задач на отражение света от плоского зеркала и их решениями.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Задача №1
Плоское зеркало повернули на угол $varphi = 16 degree$ вокруг оси, лежащей в плоскости зеркала. На какой угол $eta$ повернется отраженный зеркалом луч, если направление падающего луча осталось неизменным?
Построим к задаче чертеж (рисунок 1). Обозначим плоское зеркало в начальном положении, как $AB$. Проведем перпендикуляр к его поверхности — $CO$. Отметим угол $varphi$, на который зеркало повернули, и обозначим его новое положение, как $A_1B_1$. Перпендикуляр поворачивается вместе с зеркалом на угол $varphi$ — $OC_1$.
Также обозначим на рисунке падающий луч $DO$ и угол падения $alpha$. После поворота зеркала падающий луч не меняет своего направления. Луч $OE$ отражается от зеркала под углом отражения $beta$. После поворота зеркала угол отражения отклонится от прежнего положения на угол $eta$.
Показать решение и ответ
Решение:
Рассмотрим углы падения и отражения после поворота зеркала. Из рисунка видно, что новый угол падения составляют изначальный угол падения $alpha$ и угол поворота зеркала $varphi$ (так как перпендикуляр повернулся на тот же угол):
$angle DOC_1 = alpha + varphi$.
Теперь рассмотрим новый угол падения:
$angle C_1OE_1 = (beta — varphi) + eta$.
По закону отражения света: $beta = alpha$.
Тогда мы можем записать:
$angle C_1OE_1 = alpha — varphi + eta$.
Закон преломления действует и после поворота зеркала. Значит,
$angle DOC_1 = angle C_1OE_1$.
Подставим выражения полученные выше:
$alpha + varphi = alpha — varphi + eta$.
Выразим отсюда угол, на который отклонился отраженный луч:
$eta = alpha + varphi — alpha + varphi = 2 varphi$.
Рассчитаем этот угол:
$eta = 2 cdot 16 degree = 32 degree$.
Ответ: $eta = 32 degree$.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Задача №2
Угол между плоским зеркалом и падающим на него лучом составляет $30 degree$. Чему равны углы падения и отражения луча?
Сделаем чертеж (рисунок 2). Опустим на поверхность зеркала $MN$ перпендикуляр $CO$. Обозначим падающий луч как $AO$, а отраженный луч — $OB$. Отметим угол падения $alpha$ и угол отражения $beta$. Угол между зеркалом и падающим лучом обозначим буквой $varphi$.
Показать решение и ответ
Решение:
Сделав правильный чертеж, решить такую задачу очень просто. Из него видно, что:
$alpha = 90 degree — varphi = 90 degree — 30 degree = 60 degree$.
По закону отражения света:
$beta = alpha = 60 degree$.
Ответ: $alpha = beta = 60 degree$.
Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Задача №3
На стене вертикально висит зеркало, как показано на рисунке 3. Не смотря на то, что зеркало не достает до пола, динозаврик может видеть свое отражение в полный рост. Какая длина у зеркала? Рост динозавра 152 см, а расстояние от его глаз до верхней части головы 10 см.
Показать решение и ответ
Решение:
Как вам известно, изображение в плоском зеркале любого предмета образуется от поверхности зеркала на том же расстоянии, что и сам предмет. При этом размеры изображения предмета равны по размеру самому предмету. Видим мы это изображение, когда световые лучи попадают нам в глаз.
Используя эту информацию, сделаем чертеж для решения этой задачи (рисунок 4).
- Точка $A$ — это глаз динозавра, в который попадает изображение в зеркале
- $EG$ — плоское зеркало
- $AB$ — световой луч, попадающий в глаз, от верхней точки головы динозавра
- $AD$ — световой луч, попадающий в глаз, от нижней точки ног динозавра
- $AC$ — световой луч, соединяющий глаз динозавра и его изображение в плоском зеркале. Он будет проходить перпендикулярно зеркалу.
Отрезок $BD$ равен росту динозавра. Он состоит из двух отрезков: $BC$ и $CD$.
$BC = 10 space см$ — расстояние от верхней точки головы до глаз.
$CD = 152 space см — 10 space см = 142 space см$ — расстояние от глаз до нижнего края ног.
Сначала рассмотрим треугольники $AEF$ и $ABC$. Они будут подобны друг другу по двум углам: $angle EFA = angle BCA = 90 degree$ и $angle EAF = angle BAC$ (это один и тот же угол для двух треугольников).
Определим коэффициент подобия:
$AF = k cdot AC$.
Расстояния от предмета до зеркала и его изображения до зеркала равны. Поэтому $AC = 2AF$.
Тогда, $AF = k cdot 2AF$.
Значит, $k = frac$.
Зная коэффициент подобия $k$, запишем соотношение для других сходственных сторон:
$EF = k cdot BC = frac cdot 10 space см = 5 space см$,
т. к. по условия расстояние от глаза до верхней точки головы составляет $10 space см$. Это утверждение справедливо и для изображения динозавра.
Теперь рассмотрим треугольники $AFG$ и $ACD$. Они также будут подобны по двум углам, и коэффициент подобия будет равен $k = frac$.
Тогда, $FG = k cdot CD = frac cdot 142 space см = 71 space см$.
Теперь мы можем найти длину зеркала:
$EG = h = EF + FG = 5 space см + 71 space см = 76 space см$.
Ответ: $h = 76 space см$.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Задача №4
Две лампочки находятся в точках $A$ и $B$, как показано на рисунке 5. Постройте такое положение глаза человека перед зеркалом, при котором он увидит изображения лампочек совмещенными.
Показать построение и пояснения
Построение:
Изначально нам необходимо построить изображения этих светящихся точек (лампочек).
Из точки $A$ опустим перпендикуляр на плоское зеркало и продолжим его за зеркало. Отложим на нем расстояние по другую сторону зеркала, равное расстоянию от точки $A$ до зеркала. Получим изображение светящейся точки $A_1$.
То же самое проделаем для точки $B$ и получим ее изображение $B_1$ (рисунок 6).
В условии задачи сказано, что изображения этих точек совпадут друг с другом. Мы же видим изображения, когда нам в глаз попадают световые лучи от этих точек. Это означает, что луч должен быть один сразу для обоих точек.
Соединим точки $A_1$ и $B_1$ друг с другом и продолжим эту прямую. Со стороны от зеркала, где находятся лампочки, мы можем поставить точку на этой прямой на любом расстоянии от зеркала. Так мы получили точку $E$ — положение глаза наблюдателя, при котором он увидит лампочки совмещенными друг с другом.
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Задача №5
Солнечные лучи образуют с поверхностью стола угол $varphi = 50 degree$ (рисунок 7). Под каким углом к поверхности стола надо расположить зеркало, чтобы направить солнечный зайчик в горизонтальном направлении?
Показать решение и ответ
Решение:
Условие задачи говорит, что отраженный луч (солнечный зайчик) должен идти горизонтально. В таком случае у него может быть два направления: горизонтально влево и горизонтально вправо. Решим задачу для обоих случаев.
- Сначала рассмотрим ситуацию, где отраженный луч пойдет горизонтально вправо. Сделаем чертеж (рисунок 8).
- $MN$ — поверхность стола
- $AB$ — плоское зеркало
- $DO$ — падающий луч
- $alpha$ — угол падения
- $varphi$ — угол, образованный падающим лучом и поверхностью стола. Мы обозначили его, используя продолжение отраженного стола, параллельному столу. В этом случае продолжение отраженного луча и поверхность стола — две параллельные прямые, а падающий луч — секущая. Соответственные углы равны
- $OE$ — отраженный луч
- $beta$ — угол отражения
- $OC$ — перпендикуляр, опущенный в точку падения луча на поверхность зеркала
- $eta$ — искомый луч наклона зеркала
Из чертежа видно, что:
$varphi + alpha + beta = 180 degree$.
По закону отражения света: $alpha = beta$. Тогда,
$varphi + 2 alpha = 180 degree$,
$alpha = frac = 65 degree$.
Снова рассматривая $AB$ как секущую двух параллельных прямых, мы можем сказать, что $angle EOB = eta$.
Тогда, $eta = angle EOB = 90 degree — beta = 90 degree — alpha = 90 degree — 65 degree = 25 degree$.
- Рассмотрим второй случай, когда отраженный луч пойдет горизонтально влево. Так же сделаем чертеж (рисунок 9).
- $MN$ — поверхность стола
- $AB$ — плоское зеркало
- $DO$ — падающий луч
- $alpha$ — угол падения
- $varphi$ — угол, образованный падающим лучом и поверхностью стола. Мы обозначили его, используя продолжение отраженного стола, параллельному столу. В этом случае продолжение отраженного луча и поверхность стола — две параллельные прямые, а падающий луч — секущая. Соответственные углы равны
- $OE$ — отраженный луч
- $beta$ — угол отражения
- $OC$ — перпендикуляр, опущенный в точку падения луча на поверхность зеркала
- $eta$ — искомый луч наклона зеркала
Рассмотрим $angle COA$. Это прямой угол, образованный перпендикуляром $OC$ и поверхностью зеркала $AB$. Он состоит из двух углов: $beta$ и $angle EOA$. Угол $eta$ и $angle EOA$ равны друг другу, т .к. это накрест лежащие углы, образованные секущей и двумя параллельными прямыми.
По закону отражения света: $alpha = beta$.
Из чертежа: $varphi = alpha + beta = 2 alpha$. Т.е., $alpha = frac$.
Тогда,
$eta = angle EOA = angle COA — beta = angle COA — alpha = angle COA — frac = 90 degree — frac = 65 degree$.
Ответ: $eta_1 = 25 degree$, $eta_2 = 65 degree$.
Видео:Урок 198 (осн). Отражение света. Законы отраженияСкачать

Решение типовых задач контрольной работы по разделам 1 и 2
Тема «Функции нескольких переменных» будет рассмотрена после определенного интеграла.
1. ЛИНЕЙНАЯ АЛГЕБРА
1.1. Действия с матрицами
1.1.1. Выполнить действия
Сначала умножаем матрицу на число, а затем вычитаем из одной матрицы другую
б) нужно перемножить две матрицы: С = AS. Это возможно в случае, если число столбцов матрицы А равно числу строк матрицы S. Элемент Cjk матрицы С имеет вид:
(г = 1, 2, . и; к = 1, 2, . и), т. е. элемент матрицы С, стоящей в г-й строке и к-м столбце, равен сумме произведений соответственных элементов г-й строки матрицы А и к-го столбца матрицы S.
Справа от определителя приписываются два первых столбца, берутся со знаком «+» три произведения элементов, стоящих на главной диагонали и двух диагоналях ей параллельной и со знаком минус три произведения элементов, стоящих на побочной диагонали и двух диагоналях ей параллельной;
б) разложением по строке.
Определитель D равен сумме произведений всех элементов произвольной его строки на их алгебраические дополнения
где Aj — алгебраическое дополнение элемента определителя Яу, равное
1.2.1. Убедимся, что определитель D равен нулю
а) по определению (одной из схем):
Здесь Mj — минор элемента Яу, т. е. определитель (n — 1)-го порядка, получающийся после вычеркивания из определителя n-го порядка i-й строки и у-го столбца.
Вычисляем определитель D разложением по элементам первой строки
1.3. Обратная матрица
1.3.1. Найти обратную матрицу к матрице А и проверить выполнение равенства А ¦ A1 = £:
то матрица А является невырожденной и для нее существует об-
ратная матрица А 1.
Находим алгебраические дополнения для определителя Д:
Составляем матрицу из этих алгебраических дополнений и транспонируя ее, получаем присоединенную матрицу (А*):
Вычисляем обратную матрицу А
Так как А ¦ А 1 = то обратная матрица найдена правильно;
Находим алгебраические дополнения
Отсюда: х = 1,5; у = 3.
1.4.1. Записать систему в матричном виде Ах = b :
и решить ее средствами матричного исчисления.
Решение этой системы через обратную матрицу А 1 имеет вид
В пункте 1.3.1: а) была найдена обратная матрица А 1, тогда
Можно сделать проверку, т. е. подставить найденные значения х и у в исходную систему уравнений.
1.4.2. Решить систему методом исключения переменных (методом Гаусса):
Выберем в качестве первого ведущего уравнения — первое уравнение системы и оно в дальнейшем остается без изменения, а в качестве первого ведущего неизвестного — хь
Исключаем неизвестную х1 из второго и третьего уравнений системы с помощью первого уравнения. Для этого из 1-го уравнения вычитаем второе, получим х2 + 2х3 = 0, затем 1-ое уравнение умножаем на 3, а 3-е уравнение — на 2 и вычитаем из одного другое, получим 2х2 + х3 = 3.
Неизвестная х1 исключена. Первый шаг закончен. Теперь второе уравнение берется за ведущее и оно в дальнейшем не изменяется, а за ведущую неизвестную принимается х2. Исключаем из 3-го уравнения х2, для этого 2-ое уравнение умножаем на 2 и вычитаем из него 3-е уравнение системы, получаем 3х3 = -3.
Прямой ход метода Гаусса закончен. Обратным ходом получаем:
Итак, х1 = 4, х2 = 2, х3 = -1.
1.4.3. Дана система
Рассмотрим минор 2-го порядка
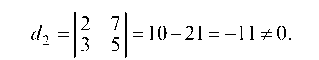
Так как миноры d^, и d| равны нулю, то ранг системы
равен двум, а так как минор = 0, то и ранг расширенной матрицы равен двум. Равенство рангов расширенной матрицы и матрицы системы на основании теоремы Кронекера—Капелли говорит о том, что система алгебраических уравнений совместна, т. е. имеет решение.
2. Найти общее решение системы в виде
Так как число неизвестных пять, а ранг матрицы равен двум, то разность между ними, равная трем (n — r = 5 — 2 = 3), говорит
о том, что три неизвестных будут свободными, пусть это будут x3, x4, x5.
Берем первые два уравнения системы и записываем их относительно x1 и x2 (коэффициенты при этих неизвестных составляют минор 2-го порядка отличный от нуля), а неизвестные x3, x4, x5 переносим в правую часть:
Имеем систему двух уравнений с двумя неизвестными x1 и x2. Умножая первое уравнение на 5, а второе на 7 и вычитая одно из другого, найдем x1 и подставляя его в 1-ое уравнение, после преобразований получим выражение для x2:
3. Найти частное решение системы a = (х1, х2, х3, х4, х5), положив х3 = 5, х4 = 2, х5 = 3 и проверить систему.
Находим х1 и х2:
Следовательно, частное решение имеет вид:
Подставляем в исходную систему значенш
Выполнение тождества для всех уравнений системы говорит о том, что вектор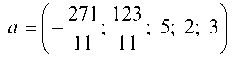
нием исходной системы уравнений.
1.5. Собственные числа и собственные векторы
1.5.1. Найти собственные числа и соответствующие им собственные векторы для матрицы
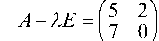
отсюда (5 — 1) ¦ (-1) — 2 ¦ 7 = 0, или I2 — 51 — 14 = 0. Корни этого уравнения 1 = -2 и 12 = 7 и являются собственными числами.
Для отыскания собственных векторов используем систему уравнений
Полагая 1 = 11 = -2, получаем систему уравнений для первого собственного вектора U(M1, M2):
Следовательно, первым собственным вектором, определяющим первое собственное направление, является
Меняя M2, будем получать различные векторы, лежащие на одной прямой (коллинеарные). Все они — собственные.
Полагая 1 = 12 = 7, получаем систему уравнений для отыскания координат второго собственного вектора V (V1; v2):
Отсюда v1 = v2 — общее решение (v2 — свободная, v1 — базисная переменная).
Второй собственный вектор V(V1; v2) = (v2; v2) = V2 (1; 1) определяет второе собственное направление.
2.1. Прямая линия на плоскости
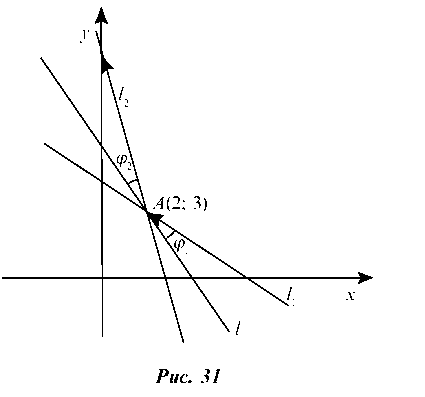
2.1.1. На прямую /: 3x + 2y — 12 = 0, которая способна отражать лучи, падает луч, заданный уравнением I1: 3x + 4y — 18 = 0. Составить уравнение отраженного луча.
Решение. Так как угол падения луча равен углу отражения луча, то Zj = Z j2, т. е. tg j1 = tg j2 (рис. 31).
Уравнение отраженного луча — прямой /2 — ищем в виде: y — yA = k2(x — xa).
Для нахождения координат точки А решим систему уравнений:
Вычитая, найдем: -2у + 6 = 0, у = 3 и 3x = 12 -2у = 12 — 2 ¦ 3 = 6, x = 2, т. е. xA = 2 и yA = 3.
Найдем угловые коэффициенты прямых / и /1:
Запишем тангенс угла между прямыми / и /1:
Для нахождения углового коэффициента прямой /2 запишем тангенс угла между прямыми / и /2 и учтем, что tg Р1 = tg (pi-
Отсюда Т огда искомое уравнение отраженного луча
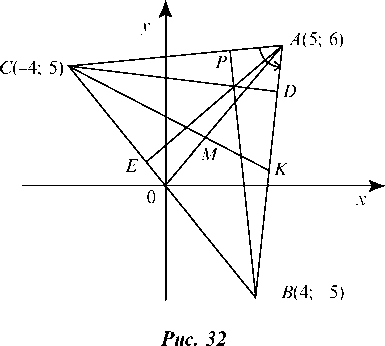
2.1.2. Дан треугольник АВС с вершинами А(5; 6), B(4; -5), C(-4; 5) (рис. 32).
Найдем уравнения всех сторон треугольника и их угловые коэффициенты.
Уравнение прямой AS:
отсюда 11 ¦ х — у — 49 = 0 или у = 11х — 49 и угловой коэффициент прямой AS равен: Kab = 11.
Уравнение прямой AC:
Уравнение прямой SC: отсюда
а) вычислим величину внутреннего угла А треугольника:
отсюда ZA = 78°27’55» = 1,37 (с точностью до 0,01) радиан;
б) найдем точку M пересечения медиан.
Определяем координаты точек K и O, делящих стороны AS и SC попалам:
Уравнение медианы CK:
отсюда
Уравнение медианы AO:
отсюда
Решая систему уравнений, описывающих медианы CK и AO, найдем координаты точки M:
в) находим точку Р пересечения высот CD и AE.
Уравнение высоты CD ищем в виде: y — yC = KCD(x — xC) и так как прямая CD L прямой AS, то
Уравнение высоты AE берем в виде: y — yA = KAE(x — xA) и так как прямая AE L прямой SC, то
г) определяем длину высоты треугольника А£, опущенной из вершины А на сторону SC, для чего запишем нормальное уравнение прямой SC:
е) находим систему линейных неравенств, определяющих внутреннюю область треугольника ASC вместе с границами.
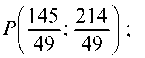
Тогда длина высоты А£ равна:
д) площадь треугольника найдем по формуле:
Имеем:
Берем любую точку, лежащую внутри треугольника ASC, например, точку (1; 1) и подставляем ее координаты в левую часть уравнений сторон: 11 ¦ 1 — 1 — 49 = -39 0;
1 — 9 ¦ 1 + 49 = 41 > 0, следовательно, система неравенств имеет вид:
Видео:Законы преломления и отражения | Оптика | ЕГЭ по физике | Николай Ньютон. ТехноскулСкачать

Геометрия световых лучей
Что нужно для уверенного решения конкурсных задач по геометрической оптике?
Во-первых, знание законов геометрической оптики:
– В однородной прозрачной среде свет распространяется прямолинейно.
– Угол отражения равен углу падения; падающий луч, луч отражённый и перпендикуляр, восставленный в точке падения, лежат в одной плоскости.
– Произведение абсолютного показателя преломления среды на синус угла между лучом света и нормалью к границе раздела двух сред при переходе света из одной среды в другую постоянно; падающий луч, луч преломлённый и перпендикуляр, восставленный в точке падения, лежат в одной плоскости.
Учитываем также, что световые лучи обратимы: при перемене местами источника и приёмника света траектория распространения света остаётся прежней.
Статья подготовлена при поддержке компании «Премьер-Девелопмент». Если вы решили приобрести качественную и надежную квартиру, то оптимальным решением станет обратиться в компанию «Премьер-Девелопмент». Перейдя по ссылке: «Новостройки в Подмосковье», вы сможете, не отходя от экрана монитора, узнать более подробную информацию о ценах и акциях, действующих на данный момент. В компании «Премьер-Девелопмент» работают только высококвалифицированные специалисты с огромным опытом работы с клиентами.
Во-вторых, необходимо знание основных положений геометрии и формул тригонометрии. Оптика ведь геометрическая! Перечислять их нет смысла. Отметим лишь, что геометрические и тригонометрические «изыски» заведомо не требуются. Однако надо твёрдо помнить, что синус и тангенс угла 

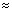
В-третьих, как и при решении геометрических задач, аккуратный и разборчивый чертёж – наш незаменимый помощник. Он должен быть достаточно крупным, чтобы чётко были видны все элементы. Используем транспортир, циркуль и линейку. От руки можно рисовать лишь весьма простые чертежи.
В-четвёртых, самое главное – необходим навык решения достаточного числа средних и трудных задач. К чему и приступим.
Задача 1 (МПГУ). Под каким углом должен упасть луч на стекло, чтобы преломлённый луч оказался перпендикулярным отражённому? Показатель преломления стекла n = 1,8.
Решение. Пусть искомый угол равен 
sin 








Вычисления дают 
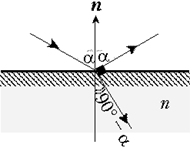
Задача 2 (Московский государственный институт электронной техники). Сечение стеклянной призмы имеет форму равностороннего треугольника. Луч падает на одну из граней перпендикулярно к ней. Вычислите угол между этим лучом и лучом, вышедшим из призмы. Показатель преломления стекла n = 1,5.
Решение. Так как луч падает на первую грань призмы по нормали к ней, то в точке D он не преломляется и прямолинейно доходит до точки E. Запишем для этой точки закон преломления: 1,5 sin 60° = sin 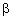
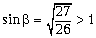
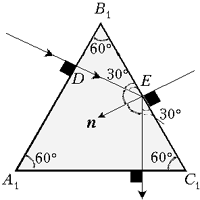
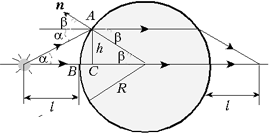
Задача 3 (МГТУ им. Н.Э.Баумана). Стеклянный шар (показатель преломления n) освещается узким расходящимся пучком лучей, ось которого проходит через центр шара. Источник света расположен на расстоянии l от поверхности. На таком же расстоянии от поверхности, но по другую сторону от шара, находится изображение источника. Определите радиус шара.
Решение. Изображение источника света находится, очевидно, в точке пересечения любого луча пучка и осевого луча.
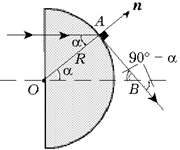
Главное – сообразить, что в силу симметрии источника света и его изображения относительно центра шара и обратимости световых лучей, луч внутри шара пойдёт горизонтально. Чтобы не загромождать выкладки, сразу пренебрегаем длиной отрезка BC по сравнению с радиусом шара. По закону преломления света в точке A и из очевидных на рисунке треугольников, имеем систему уравнений:
При замене синуса и тангенса малых углов самими углами система радикально упрощается:
Подставляя из второго и третьего уравнений углы 
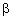
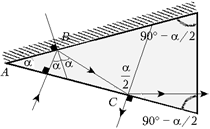
Задача 4. Сечение стеклянной призмы имеет форму равнобедренного треугольника. Одна из больших граней посеребрена. Луч света падает нормально на другую большую непосеребрённую грань и после двух отражений выходит через основание призмы перпендикулярно ему. Найдите углы призмы.
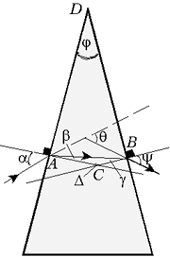
Решение. На рисунке показан ход луча в призме, неизвестный угол при вершине которой обозначен 

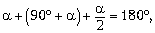

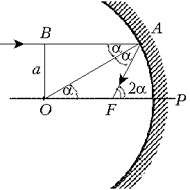
Задача 5. Найдите фокусное расстояние вогнутого сферического зеркала радиусом R для луча, падающего на зеркало параллельно главной оптической оси на расстоянии a от неё.
Решение. Геометрическая конфигурация задачи ясна из рисунке. В равнобедренном треугольнике AOF легко выразить боковую сторону OF через основание OA = R и угол при нём 
Из прямоугольного треугольника OBA находим:
Тогда 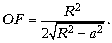
Видим, что оно зависит от a, т.е. для разных лучей будет разным. Однако для параксиальных лучей 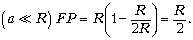
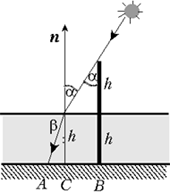
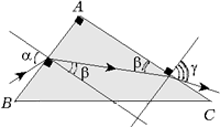
Задача 6. Свая длиной 2 м выступает над поверхностью воды на h = 1 м. Определите длину тени от сваи на дне озера, если угол падения лучей света составляет 
Из рисунка видно, что длина тени – отрезок AB – равен сумме длин отрезков BC и AC. Очевидно, что BC = h tg 
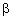

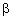
По закону преломления света, n sin 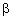

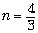
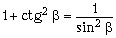
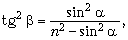
Числовой расчёт даёт AB 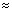
Задача 7 (МГТУ им. Н.Э.Баумана). Луч света падает на трёхгранную призму под углом 
Призма сделана из стекла с показателем преломления n. Преломляющий угол при вершине призмы 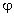
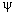
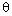
Решение. По закону преломления, sin 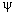
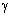
По теоремам о сумме углов треугольника ABC и четырёхугольника ADBC, соответственно имеем:
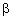
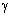
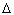
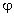
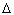
откуда 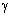
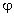
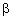
sin 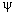
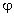
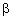
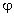
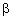
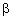
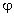
По закону преломления,
По основному тригонометрическому тождеству,
Чтобы не было претензий на экзамене (по сути, формальных), разумно записать:
Так как внешний угол треугольника равен сумме двух его внутренних углов, с ним не смежных, то
Но ранее найдено 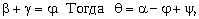
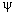
Задача 8 (физфак МГУ им. М.В.Ломоносова, 1994). Шар радиусом R из стекла с показателем преломления n разрезан по диаметру. На диаметральную плоскость одной из половин шара нормально падает параллельный пучок света. На каком расстоянии от центра шара пересекут главную оптическую ось лучи, прошедшие сферическую поверхность на наибольшем удалении от этой оси?
Решение. Ход луча, удовлетворяющего условию задачи, изображён на рисунке.
Отметим, что для него луч, преломлённый в точке A, пойдёт перпендикулярно радиусу OA и пересечёт главную оптическую ось в точке B. По закону преломления, 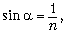
Задача 9 (ВМК МГУ им. М.В.Ломоносова, 1990). Луч света, лежащий в плоскости рисунка, падает на боковую грань AB призмы, имеющей при вершине угол 90°. В каких пределах лежат возможные значения угла падения 
По закону преломления луча на гранях призмы AB и AC, имеем систему уравнений:
Чтобы луч не испытал полное внутреннее отражение на грани AC, необходимо выполнение условия sin 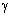
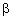
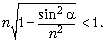
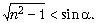
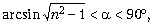


🎬 Видео
Отражение света, законы отражения, плоские зеркала. 8 класс.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Математика 5 класс (Урок№21 - Прямая, луч, отрезок.)Скачать

Отрезок, луч, прямаяСкачать

Преломление света, закон преломления света, полное внутреннее отражение. 8 класс.Скачать

Отражение света, законы отражения, плоские зеркала. Практическая часть - решение задачи. 8 класс.Скачать

Закон прямолинейного распространения света. Практическая часть - решение задачи. 8 класс.Скачать

Видеоурок "Канонические уравнения прямой"Скачать

11. Прямая в пространстве и ее уравненияСкачать

Ход лучей через призмуСкачать

Уравнение прямой.Скачать

Видеоурок "Общие уравнения прямой"Скачать