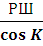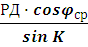- Глава 4
- § 28. Локсодромия
- Для вывода уравнения локсодромии рассмотрим элементарный треугольник АВF на земном эллипсоиде, образованный отрезками меридиана АF, параллели FB и локсодромии AF, составляющей с меридианами одинаковые углы К. По малости сторон треугольник АВF можно принять за плоский и тогда
- Произведя необходимые преобразования подынтегрального ∫ ▾ ▽ cos φ dφ / (1 — e²sin²φ) выражения, как показано в предыдущем параграфе, получим уравнение локсодромии АВ на карте проекции Меркатора с учетом сжатия Земли
- ═ — ╏ = tg K (D2 — D1). (89)
- Последнее уравнение показывает, что локсодромия на проекции Меркатора изображается прямой линией. Иначе и быть не может, так как систему параллельных между собой прямых (меридианов) под одним углом пересекает только прямая линия. Приняв одну из точек, через которые проходит локсодромия, на экваторе, т. е. считая ▽ = 0 и ╏ = λo, а координаты произвольной точки В текущими, т.е. ▾ = φ и ═ = λ, перепишем уравнение локсодромии в следующем виде (формулы 90):
- Тема 1.12 Локсодромия и ортодромия.
- Вычисление локсодромического курса, начальных и конечных курсов для ДБК.
- 📹 Видео
Глава 4
ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ, ПРИМЕНЯЕМЫЕ ДЛЯ ПОСТРОЕНИЯ МОРСКИХ НАВИГАЦИОННЫХ КАРТ
§ 28. Локсодромия
Траектория корабля, идущего неизменным курсом, представляет собой на Земной поверхности линию двоякой кривизны, пересекающую все меридианы под одним и тем же углом. Такая кривая называется локсодромией, что в переводе с греческого означает «косой бег» (рисунок). Локсодромия на поверхности Земли спиралеобразно приближается к полюсу, но никогда его не достигает.
Для вывода уравнения локсодромии рассмотрим элементарный треугольник АВF на земном эллипсоиде, образованный отрезками меридиана АF, параллели FB и локсодромии AF, составляющей с меридианами одинаковые углы К. По малости сторон треугольник АВF можно принять за плоский и тогда
tg K = rΔλ / MΔφ = NcosφΔλ / MΔφ.
Переходя от элементарно малых величин Δφ и Δλ к их дифференциалам, последнее выражение перепишем в виде
dλ = tg K * (dφ / cos φ).

Произведя необходимые преобразования подынтегрального ∫ ▾ ▽ cos φ dφ / (1 — e²sin²φ) выражения, как показано в предыдущем параграфе, получим уравнение локсодромии АВ на карте проекции Меркатора с учетом сжатия Земли
═ — ╏ = tg K [ ln tg (45° + ▾) — ln tg (45° + ▽ / 2) ] — e tg K [ln tg (45° + ◒ / 2) — ln tg (45° + ◑) ,]
окончательный вид которого будет
═ — ╏ = tg K [ ln tg (45° + ▾ / 2)<(1 — esin ▾) / (1 + e sin ▾) e/2 — ln tg (45° + ▽ / 2) * < ( — esin ▽ / (1 + e sin ▽) e/2 ]
где ▽, ╏, ▾, ═ — координаты точек, через которые проходит локсодромия.
Без учета сжатия Земли уравнение локсодромии имеет вид
═ — ╏ = tg K [ ln tg (45° + ▾ / 2) — ln tg (45° + ▽ / 2) ] (88)
Выражения, стоящие в квадратных скобках уравнений (87) и (88), представляют собой разности меридиональных частей: D2 —для параллели с широтой ▾ и D1 — для параллели с широтой ▽.
Поэтому выражения (87) и (88) могут быть представлены в виде
═ — ╏ = tg K (D2 — D1). (89)
Последнее уравнение показывает, что локсодромия на проекции Меркатора изображается прямой линией. Иначе и быть не может, так как систему параллельных между собой прямых (меридианов) под одним углом пересекает только прямая линия. Приняв одну из точек, через которые проходит локсодромия, на экваторе, т. е. считая ▽ = 0 и ╏ = λo, а координаты произвольной точки В текущими, т.е. ▾ = φ и ═ = λ, перепишем уравнение локсодромии в следующем виде (формулы 90):
— с учетом сжатия Земли:
— без учета сжатия Земли:
λ = tg K (45° + φ / 2) + λo
Выведенные уравнения позволяют по известным курсу К, долготе точки пересечения экватора λо и одной из текущих координат локсодромии вычислить вторую координату. Исследуем полученные уравнения с целью выявления свойств локсодромии.
1. Положив в формуле (87) или (88) K = 0° или K = 180°, найдем, что ═ — ╏ = 0 или ═ = ╏, т. е. λ = const. В этом случае локсодромия совпадает с меридианом и проходит через точки обоих полюсов.
2. При K = 90° или K = 270° tg K = ∞. Но так как разность долгот точек локсодромии ═ — ╏ величина конечная, то один из членов формулы (87) или (88) дол-жен быть равен нулю, т. е. ln tg (45° + ▾ / 2 ) — ln tg (45° + ▽ / 2 ) = 0,
следовательно,
▾ = ▽, то есть φ = const.
Локсодромия в этих случаях совмещается с параллелью или с экватором (при φ = 0°).
3. Уравнение (90) приведем к такому виду:
tg (45° + φ / 2) = e(λ — λo)ctg K (91)
Полученное уравнение показывает, что каждому зна ч ению широты φ соответствует только одно значение долготы λ , т. е. локсодромия пересекает каждую параллель только один раз. Придавая долготе значения λ, λ + 2π, λ + 4π, λ + 6π и т. д., будем получать каждый раз все новые возрастающие значения широты. Это означает, что локсодромия пересекает каждый меридиан бесчисленное множество раз, стремясь к полюсу и не достигая его. Исключение составляют лишь случаи, когда K =0° и K = 180°.
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Тема 1.12 Локсодромия и ортодромия.
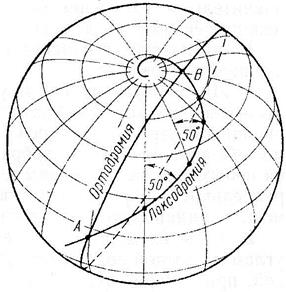
Используя навигационные морские карты, судоводители прокладывают на них путь в виде прямой линии. Из условия построения карты, такой прямой путь на карте не будет кратчайшим на местности. Путь (прямая), проложенный на карте в Меркаторской проекции называется локсодромией (кривой бег). Кратчайший же путь между двумя точками на земной поверхности эллипсоида является сложной кривой, называемой геодезической линией. На поверхности сферы (шара) кратчайшее расстояние между двумя точками измеряется по дуге большого круга, т.е. круга, образованного пересечением плоскости, проходящей через центр сферы и заданные точки, со сферической поверхностью. Такая дуга в навигации называется ортодромией.
При анализе уравнения ортодромии можно сделать следующие выводы:
2. ортодромия пересекает меридианы под разными углами;
3. при расположении точек по экватору ортодромия совпадает с экватором.
С появлением на море магнитных компасов стало удобным плавать на линии постоянного курса, что геометрические исследования в этой области. Кривую на поверхности Земли, пересекающую все меридианы под одним и тем же углом называют, как уже говорилось локсодромией. Эта кривая в математике известна как логарифмическая спираль, на навигационной карте она прямая линия, пересекающая меридианы под одним и тем же углом.
Рис. 1.23 Локсодромия и ортодромия. Разность углов, под которыми ортодромия пересекает меридианы двух точек, называется сближением (схождением) меридианов. γ = А2 – А1.
Угол схождения меридианов рассчитывается по приближенной формуле:
γ = 2arc tg [tg( 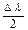
Основные свойства локсодромии:
- Если курс равен 180 или 360, то локсодромия совпадает с меридианом и ортодромией К=0. tgK = 0. l2 — l1 = 0. . l2 = l1 )
- Если курс равен 90 или 270, то локсодромия совпадает с параллелью или экватором, т.е. образует малый или большой круг на поверхности Земли.
- При любых других курсах локсодромия спиралеобразно стремится к полюсу, никогда его не достигая.
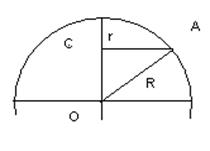
Принимая Землю за шар, можно определить отношение длины экватора и параллели в какой — либо произвольной широте j.
|
Рис. 1.24
1.12.1 Меридиональные части. Разность меридиональных частей.
При решении многих задач судовождения часто приходится рассчитывать расстояние по меридиану от экватора до любой заданной параллели или между параллелями. Пользоваться для этой цели РШ не всегда удобно, а иногда и не желательно из – за недостаточной точности получаемого результата. Поэтому в расчетах, требующих повышенной точности, чаще пользуются меридиональными частями.
Меридиональная часть (МЧ) – это расстояние на меркаторской проекции от экватора до параллели с заданной широтой φ при масштабе на экваторе, равном единице.
для навигации МЧ удобнее всего выражать через 1′ дуги экватора, т.е. в экваториальных милях. в МТ – 75 составлена табл. 26, в которой приведены значения МЧ для широт от 0 0 до 89 0 59′ через интервал в 1′ широты. Для нахождения промежуточных значений МЧ на каждую десятую долю минуты широты достаточно проинтерполировать их ближайшие табличные значения.
Разность меридиональных частей (РМЧ) – это расстояние по меридиану между двумя параллелями, выраженное в экваториальных милях. Для расчета РМЧ необходимо по табл.26 выбрать МЧ для каждой параллели φ и произвести вычитание:
На поверхности Земного шара 1′ дуги меридиана (1 м. миля) величина постоянная, на меркаторской проекции 1 м.миля изображается различными по длине отрезками в зависимости от широты, т.е. величина переменная. При удалении от экватора линейная величина увеличивается, по мере приближения к экватору – все более уменьшается и на экваторе становится равной экваториальной миле. Поэтому, измеряя расстояние на меркаторской карте, следует на вертикальной рамке карты откладывать меркаторские мили в том месте, которое соответствует широте измеряемого расстояния. В связи с этим с достаточной точностью на такой карте можно снять лишь расстояния, не превышающие нескольких десятков миль.
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Вычисление локсодромического курса, начальных и конечных курсов для ДБК.
Аналитическое счисление. Формулы аналитического счисления
Аналитическое, или письменное, счисление применяется при плавании вдали от берегов, если нет путевых карт или приходится использовать мелкомасштабные карты, во время ледового плавания, а также при решении некоторых частных задач.
Сущность письменного счисления заключается в том, что с помощью соответствующих формул вычисляют разность широт и долгот за время плавания и по ним определяют координаты пункта прихода судна по известным координатам пункта отхода:
Формулы письменного счисления позволяют решать и обратную задачу: определить курс и расстояние между двумя точками по их известным координатам. Аналитическое счисление точнее графического, так как в нем исключаются ошибки графических построений.
Однако оно менее наглядно.
Для получения формул письменного счисления проложим от точки А — пункта отхода в точку В — пункт прихода на меркаторской карте курс судна, представляющий собой отрезок локсодромии. Географические координаты пункта отхода φ1 и λ1 известны, известно также плавание судна S. Необходимо определить координаты пункта прихода φ2 и λ2.Проведем меридиан пункта отхода А и параллель пункта прихода В и рассмотрим получившийся треугольник АВС.
Стороны АВ и АС этого треугольника измеряются в одних и тех же единицах — в морских милях. Причем, чем больше широта района плавания, тем больше линейная длина морской мили. Однако это увеличение происходит пропорционально для обеих сторон АВ и АС. Следовательно, перемещение судна в направлении меридиана выражено всегда в одинаковых мерах длины по отношению к плаванию S и может быть найдено простым решением прямоугольного треугольника:
АС = АВ cosK = S cosK
Линия АС — это дуга меридиана, заключенного между параллелями пункта отхода и пункта прихода, выраженная в морских милях, и, следовательно, представляет собой разность широт, т, е.
Таким образом, разность широт всегда может быть найдена как произведение плавания на косинус курса.
Что же касается перемещения судна от точки А до точки В вдоль параллели, то подобным решением через плавание S оно найдено быть не может. Дело в том, что плавание S от φ1 до φ2 выражается в изменяющихся по линейной величине морских милях, а перемещение судна вдоль параллели СВ — в милях, постоянных для данной широты φ2. Учитывая свойства меркаторской проекции, становится очевидным, что перемещение судна по линии СВ, выраженное в морских милях, будет меньшим (так как в φ2 линейная величина мили длиннее), а перемещение АF — большим (так как в φ1 линейная величина мили короче и в одном и том же отрезке их укладывается больше).
Для устранения этого несоответствия поступают следующим образом. Проводят среднюю параллель φср (рис.) между точками А и В.
Теперь, если предположить что уменьшение линейной длины морской мили от φср к параллели точки А происходит в той же последовательности и в тех же пределах, что и увеличение её от φср к параллели точки В, то с достаточной точностью можно считать, что и плавание S, и расстояние С׳В׳ выражены в одних и тех же единицах длины. В этом случае:
В аналитическом счислении эта величина получила название отшествия (ОТШ):
Отшествие не является разностью долгот, так как РД выражается в экваториальных милях. Для перехода от отшествия к РД на основании зависимости между длиной экватора и длиной параллели используют формулу
Допущение о том, что отшествие равно длине средней параллели, справедливо лишь для малых широт и при сравнительно небольшом плавании. Более строгие расчеты показывают, что для увеличения точности аналитического счисления следует использовать формулу
Разность меридиональных частей (РМЧ) может быть использована для нахождения разности долгот и по другой точной формуле. В этом случае после определения φ2 выбирают меридиональные части для широт φ2 и φ1 и, найдя их разность, из прямоугольного треугольника АВС (рис.) получают
Разность меридиональных частей выражается в экваториальных милях, поэтому и СВ будет в экваториальных милях, а значит будет являться разностью долгот:
Недостатком этой формулы является то, что на курсах, близких к 90° и 270°, когда тангенс начинает изменяться очень быстро, даже небольшие ошибки в курсе могут привести к значительным ошибкам в искомой РД.
Аналитическое счисление.
Формулы аналитического счисления
Расчет длин локсодромии и ортодромии.
Вычисление локсодромического курса, начальных и конечных курсов для ДБК.
При курсах в четвертном счете до 45 0 для вычисления Sлок служит формула
Sлок =
где: РШ – разность широт начального (φн) и конечного (φк) ;
К – локсодромический курс между пунктами плавания, причем:
tg K = 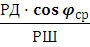

здесь РД – разность долгот начального (λн) и конечного (λк).
При курсах в четвертном счете более 45 0 локсодромическое расстояние с достаточной точностью можно найти, используя линейный широтный масштаб карты, либо аналитическим решением:
Sлок =
Длину ортодромии Sорт вычисляем по формуле:
cos Sорт = sin φн ∙ sin φк + cos φн ∙ cos φк ∙ cos РД
При анализе этой формулы на знаки принимаются следующие условия:
| Обозначение | Название | Условие | Знаки | |
| sin | cos | |||
| φ | Широта | N S | + — | + + |
| РД | Разность долгот | РД 0 РД > 90 0 | + — |
Для определения начального Кн и конечного Кк курсов, при расчетах плавания по дуге большого круга, применяются формулы:
sin Кн = 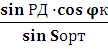
📹 Видео
Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнение плоскости. 11 класс.Скачать

Геометрический смысл производной. Уравнение касательнойСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 13.4. Существов. и единств. решения ДУСкачать

9 класс, 5 урок, Уравнение линии на плоскостиСкачать

Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Алгоритм ЕвклидаСкачать

Урок 218. Напряженность электрического поляСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 2Скачать

Предельные вероятности состоянийСкачать

✓ Критерий Коши сходимости числовых последовательностей | матан #013 | Борис Трушин |Скачать