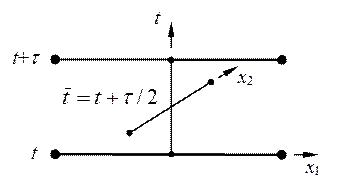Локально одномерный метод для многомерного уравнения теплопроводности

Экономичные схемы. Для уравнения переноса (лекция №10) хорошие схемы бегущего счета естественным образом обобщаются на многомерный случай. Для уравнения теплопроводности попытки обобщить хорошие неявные разностные схемы типа (6), (19),(20) на многомерный случай сталкиваются с принципиальными трудностями.

Рассмотрим эти затруднения на примере двумерного уравнения теплопроводности с постоянным коэффициентом теплопроводности, для которого определена первая краевая задача в прямоугольной по переменным x₁, x₂ области:

, (34)

; (35)

(36)

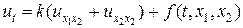
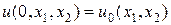
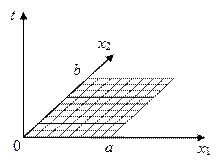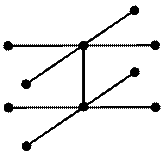Рис.6,а. Определение прямоугольной равномерной сетки с шагами h1, h2 по переменным x1, x2	Рис.6,б. Шаблон разностной схемы (37)

Определим прямоугольную сетку (x_1,n,x_2,m) (рис.6,а), считая для простоты ее равномерной с шагами по переменным x₁, x₂ — h₁, h₂ соответственно, т.е. x_1,n = h₁n, x_2,m = h₂m, n = 0,1,…,N, m = 0,1,…,M. Выберем в качестве шаблона разностной схемы тот, который представлен на рис.6,б. На каждом временном слое шаблон имеет форму креста, по которому составляется неявная двухслойная схема с весом s, построенная по аналогии со схемой (6), т.е.

, (37)

(37¢)

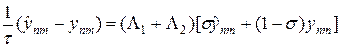
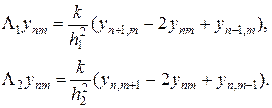
Запись начального (35) и краевых условий (36) в разностном виде очевидна и реализуется точно. Можно проверить, что погрешность аппроксимации схемы (37), (37¢) на решениях с непрерывными четвертыми производными равна 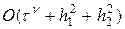, где n = 2 при s = ½ и n = 1 при s ¹ ½.

Исследуем устойчивость разностной схемы (37), (37¢) методом разделения переменных. Гармоники с текущего и следующего временного слоя выберем в виде:

,

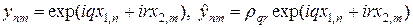
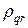
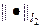
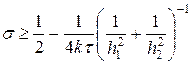
тогда, считая как обычно модуль множителя роста меньше единицы, находим условие устойчивости разностной схемы (37), (37¢) в :

, (38)

которое похоже на аналогичное условие (10) для одномерной схемы (6).

Схема (37), (37¢) легко обобщается на случай p измерений. Оценим число операций, требуемых для расчета до момента времени T.

Рассмотрим явную схему при s = 0, для которой значения 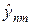вычисляются по значениям с предыдущего слоя, т.е. всего требуется

N p операций, где для простоты считается, что число узлов по каждой переменной одинаково и равно N. Согласно (38), явная разностная схема устойчива, когда

.

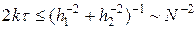
Таким образом, для расчета до момента времени T необходимо сделать

N 2 шагов по времени и полный расчет потребует

Если пользоваться абсолютно устойчивой схемой, когда s ³ ½, то можно выбирать t

h. Однако, в этом случае необходимо решать линейную систему уравнений порядка N p . Если ее решать методом Гаусса, то потребуется

N 3 p операций. Это число операций можно несколько сократить, заметив, что полученная матрица будет сильно разреженной и если предположить, что используется алгоритм, учитывающий такую разреженность, то число операций будет

N 3 p — 2 . Такая оценка следует из того, что в одномерном случае матрица трехдиагональная и система уравнений решается прогонкой с числом операций

N. Учитывая, что для получения решения в момент времени T требуется

N шагов по времени, найдем итоговую оценку для числа операций

N 3 p — 1 при использовании неявной разностной схемы.

Если для одномерного уравнения явная схема является явно невыгодной на фоне использования неявных схем, то в многомерном случае (p ³ 2) неявные схемы становятся невыгодными по сравнению с явной схемой.

Несмотря на упомянутые выше трудности, для многомерного параболического уравнения построены абсолютно устойчивые разностные схемы, которые позволяют вести расчет с шагом t

N p операций для перехода со слоя на слой. Это значит, что число действий в расчете на узел пространственной сетки не зависит от шагов h_a, a = 1,…,p. Такие схемы принято называть экономичными.

Подавляющее большинство многомерных расчетов параболических уравнений производится по экономичным схемам. Ниже будут рассмотрены два вида таких схем: продольно-поперечные и локально-одномерные.

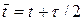
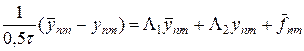
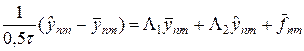
Продольно-поперечная схема является одной из самых лучших двумерных экономичных разностных схем. Ее также называют схемой переменных направлений. На рис.7 приведен шаблон схемы переменных направлений, в которую введен полуцелый слой . Составим согласно шаблону рис.7 разностную схему:

, (39)

, (39¢)

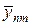
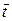
где разностные операторы L₁, L₂ определены в (37¢), а берется на полуцелом слое .

Рис.7. Шаблон разностной схемы (39), (39¢)

Исследуем продольно-поперечную разностную схему (39), (39¢).

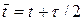
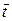
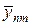
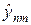
Вычислительная процедура по схеме (39), (39¢) складывается из перехода со слоя t на слой согласно уравнению (39) и далее переход со слоя на слой t + t согласно уравнению (39¢). На первом шаге неизвестными выступают величины с полуцелого слоя, они находятся прогонкой по направлению x₁ путем обращения разностного оператора L₁, который согласно (37¢) определен на трехточечном шаблоне. На втором шаге при переходе на слой t + t неизвестными выступают величины , они находятся прогонкой, но в поперечном x₂ направлении путем обращения оператора L₂, который также определен на трехточечном шаблоне. И для первой, и для второй прогонки имеется диагональное преобладание так, что прогонки устойчивы, а разностное решение существует и единственно.

Устойчивость продольно-поперечной схемы можно исследовать методом разделения переменных. Положим

, (40)

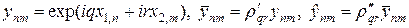
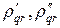
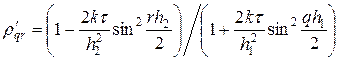
где — множители роста гармоник на первом и втором полушагах. Подставляя представление (40) в (39), (39¢), находим

, (41)

. (41¢)

Учитывая (40), (41¢), можно убедиться, что для любых гармоник и при любых шагах сетки верно неравенство: 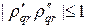. Таким образом, при переходе со слоя слой ошибки в начальных данных не растут и разностная схема (39), (39¢) равномерно и безусловно устойчива по начальным данным. Можно также проверить, что дополнительный признак устойчивости по правой части (9.65) выполняется на каждом из полушагов по времени, т.е. схема (39), (39¢) также устойчива по правой части.

Порядок аппроксимации схемы (39), (39¢) можно оценить путем исключения полуцелого слоя. Для этого вычтем из уравнения (39) уравнение (39¢), тогда найдем

. (42)

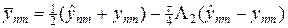
Складывая уравнения (39), (39¢) и подставляя в них выражение (42), получим

. (43)

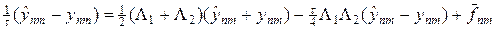
Предпоследний член в правой части (43), после разложения в ряд Тейлора, может быть аппроксимирован выражением . Остальные члены в (43) совпадают с симметричным вариантом схемы (37) (s = ½), которая имеет порядок аппроксимации . Тем самым, продольно-поперечная схема имеет второй порядок точности по всем переменным.

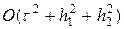
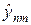
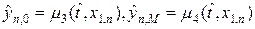
Определимся с аппроксимацией граничных условий (36) для продольно-поперечной схемы. При решении уравнения (39¢) относительно необходимо использовать граничное условие на сторонах прямоугольника x₂ = 0 и x₂ = b. В этом случае очевидно можно положить, что

. (44)

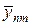
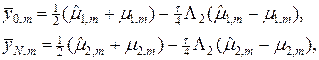
При решении уравнения (39) относительно необходимы граничные условия на сторонах x₁ = 0 и x₁ = a. Для их получения необходимо воспользоваться уравнением (42), тогда

(44¢)

где m = 1,…,M-1. Граничные условия (44), (44¢) обеспечивают погрешность аппроксимации .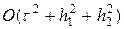

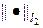
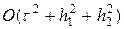
Проведенное исследование аппроксимации и устойчивости показывает, что схема (39), (39¢) безусловно сходится в норме , при этом в прямоугольной области на равномерной сетке и при граничных условиях (44), (44¢) схема имеет точность на решениях с непрерывными пятыми производными.

Изучим разностную схему (39), (39¢) на примере численного решения уравнения (34) с правой частью вида:

(45)

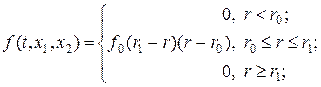
где f₀, r₀, r₁ = const > 0, а 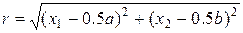. Функция (45) представляет собой источник тепла эллиптической формы в области [0,a]´[0,b]. Трехмерный график источника тепла представлен на рис.8 (левый рисунок). На листинге_№4 приведен код программы численного решения задачи (34), (45) с нулевыми граничными и начальными условиями.

%Программа решения двухмерного уравнения

%теплопроводности (34) с источником специального

%вида (45) с помощью продольно-поперечной

%разностной схемы (39), (39′)

global a b f0 r0 r1

%Определяем габариты области интегрирования

%по времени, направлениям x1 и x2, а также

%коэффициент теплопроводности и константу f0,

%задающую амплитуду источника

T=1; a=1; b=1; koef=0.5; f0=100;

%Определяем число шагов по времени и по

%направлениям x1 и x2

%Определяем сетки по x1 и x2

%Определяем источник тепла в узлах сетки

%Рисуем трехмерный профиль источника тепла

%Определяем нулевые начальные данные

%Определяем граничные условия при x1=0 и x1=a

%Определяем граничные условия при x2=0 и x2=b

%Определяем номера слоев по времени, которые будут

%нарисованы на итоговом графике

%Организуем основной цикл интегрирования по времени

%Находим решение на полуцелом временном слое,

%т.е. решаем уравнение (39)

%Учитываем нулевое граничное при x1=0

%Учитываем нулевое граничное при x1=a

%Находим решение на следующем временном слое,

Видео:Одномерное уравнение теплопроводности. Виды краевых задачСкачать

Локально-одномерная схема для уравнения теплопроводности с сосредоточенной теплоемкостью Текст научной статьи по специальности « Математика»

Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Аннотация научной статьи по математике, автор научной работы — Шхануков-Лафишев Мухамед Хабалович, Лафишева Мадина Мухамедовна, Нахушева Фатима Мухамедовна, Мамбетова Альбина Борисовна

Работа посвящена исследованию локально-одномерных схем для уравнения теплопроводности с

нестационарным краевым условием, когда на границе области помещена сосредоточенная теплоемкость некоторой величины. В работе получена априорная оценка в равномерной метрике, откуда следует сходимость построенной схемы на кубической сетке.

Видео:Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

Похожие темы научных работ по математике , автор научной работы — Шхануков-Лафишев Мухамед Хабалович, Лафишева Мадина Мухамедовна, Нахушева Фатима Мухамедовна, Мамбетова Альбина Борисовна

Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать

The locally-one-dimensional scheme for the equation of heat conductivity with the concentrated thermal capacity

The work is devoted to locally-one-dimensional schemes for the equation of heat conductivity with a non-stationary boundary condition which imitate a concentrated thermal capacity placed on domain boundary. A priori estimate in the uniform metrics is obtained and the convergence of the constructed scheme on a cubic net is proved.

Видео:Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

Текст научной работы на тему «Локально-одномерная схема для уравнения теплопроводности с сосредоточенной теплоемкостью»

Владикавказский математический журнал 2013, Том 15, Выпуск 4, С. 58-64

ЛОКАЛЬНО-ОДНОМЕРНАЯ СХЕМА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ С СОСРЕДОТОЧЕННОЙ ТЕПЛОЕМКОСТЬЮ

М. Х. Шхануков-Лафишев, М. М. Лафишева, Ф. М. Нахушева, А. Б. Мамбетова

Работа посвящена исследованию локально-одномерных схем для уравнения теплопроводности с нестационарным краевым условием, когда на границе области помещена сосредоточенная теплоемкость некоторой величины. В работе получена априорная оценка в равномерной метрике, откуда следует сходимость построенной схемы на кубической сетке.

Ключевые слова: краевая задача, сосредоточенная теплоемкость, локально-одномерная схема, сходимость, априорная оценка.

Локально-одномерные схемы (ЛОС) для решения многомерных задач математической физики впервые введены в рассмотрение А. А. Самарским [2]. Отказ от классического понятия аппроксимации и замена его более слабым условием суммарной аппроксимации существенно расширяет класс решаемых задач.

В работе рассмотрены ЛОС для уравнения теплопроводности, когда на границе области помещена сосредоточенная теплоемкость некоторой величины. Тогда для уравнения теплопроводности в одномерном случае, например, при x = 0 ставится краевое условие вида

du , du со^гг = к—, с0 = const > 0. dt dx

Подобные условия возникают в случае, когда рассматривается тело с большой теплопроводностью [1, с. 186], при решении задачи об установлении температуры в ограниченной среде при наличии нагревателя, трактуемого как сосредоточенная теплоемкость [2].

Аналогичные задачи возникают также в практике регулирования солевого режима почв, когда расслоение верхнего слоя достигается сливом слоя воды с поверхности затопленного на некоторое время участка [3, с. 233]. Если на поверхности поля имеется слой воды постоянной толщины h, то на верхней границе следует задать условие

где c — концентрация соли в почвенном растворе, D — коэффициент диффузивности [3].

В одномерном случае подобные задачи рассмотрены в [4, с. 426]. Здесь рассматривается случай многомерной задачи, когда на границах области по каждому направлению xa, a = 1,2 . p, помещена сосредоточенная теплоемкость величины х±а, a = 1,2. p. Для рассматриваемой задачи построена схема повышенного порядка

© 2013 Шхануков-Лафишев М. Х., Лафишева М. М., Нахушева Ф. М., Мамбетова А. Б.

аппроксимации. С помощью принципа максимума для ЛОС получены априорные оценки в равномерной метрике, выражающие устойчивость ЛОС по начальным данным, по правой части и граничным данным.

1. Локально-одномерная схема. В цилиндре С>т = С х [0,Т], где С = <ж =

(ж1 , х2. хр) : 0 ^ ха ^ 1а,а = 1. ,р> — р-мерный прямоугольный параллелепипед, рассматривается задача

— = ьи + /(х,г), (х,г)едт = Сх(о,т], (1)

где 0 0, Х±а ^ 0, а = 1. ,р.

Следуя [4, с. 520], заменим многомерное уравнение цепочкой одномерных уравнений теплопроводности

p dt с условиями

— ka(x, t) gxaa — X+a (%, t) + /3+а (ж, í)f(a) — xa — la,

v(a)(x, 0) — u0(x), = a = 2,3. p, (6)

V(i)(x,tj) — V(p)(x,tj), j — 1,2. jo — 1.

Аппроксимируя каждое уравнение теплопроводности номера а на полуинтервале

у р = г р +п р в уравнение (7), получим

& р =Ааг3+Р + фа Р, 4>а Р =Ааи3+Р +(ра Р — Щ

Обозначим через фа = (Ьаи + /а — ^^ ) и, замечая, что ^ фа = 0, если ^ /« = /

Видео:Решение первой начально-краевой задачи для одномерного уравнения теплопроводности.Скачать

Локально-одномерная схема для уравнения теплопроводности с сосредоточенной теплоемкостью

Автор: Шхануков-Лафишев Мухамед Хабалович, Лафишева Мадина Мухамедовна, Нахушева Фатима Мухамедовна, Мамбетова Альбина Борисовна

Бесплатный доступ

Работа посвящена исследованию локально-одномерных схем для уравнения теплопроводности с

нестационарным краевым условием, когда на границе области помещена сосредоточенная теплоемкость некоторой величины. В работе получена априорная оценка в равномерной метрике, откуда следует сходимость построенной схемы на кубической сетке.

Краевая задача , сосредоточенная теплоемкость , локально-одномерная схема , сходимость , априорная оценка

Короткий адрес: https://readera.org/14318444

Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

Список литературы Локально-одномерная схема для уравнения теплопроводности с сосредоточенной теплоемкостью

• Тихонов А. Н., Самарский А. А. Уравнения математической физики.-М.: Наука, 1996.-724 c.
• Самарский А. А. Об одной задаче распространения тепла//Избр. тр. А.

Самарского.-М.: МАКС Пресс, 2003.-С. 1-22.

📸 Видео

Метод Фурье для неоднородного уравнения теплопроводностиСкачать

6-1. Уравнение теплопроводностиСкачать

12.1 Как остывает кирпич (уравнение теплопроводности)Скачать

Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Решение неоднородного уравнения теплопроводностиСкачать

Уравнение теплопроводности на полупрямой (решение задачи)Скачать

Решение уравнения теплопроводности методом конечных разностейСкачать

Решение задачи теплопроводности методом конечных разностейСкачать

Метод Фурье для уравнения теплопроводности (диффузии)Скачать

Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Решение задачи теплопроводности (Явная разностная схема)Скачать

Вывод уравнения теплопроводностиСкачать

Уравнение теплопроводности в кольцеСкачать