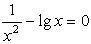Про уравнения - легко » Статьи

Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до

Обновлено
Содержание
  1. Лабораторная работа №1. Приближенное решение алгебраических и трансцендентных уравнений
  2. Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
  3. Численные методы решения нелинейных уравнений
  4. Примеры приближенных решений нелинейных уравнений онлайн
  5. 📽️ Видео

Видео:Решите уравнение sin(πx/3) = 1/2 В ответе напишите наименьший положительный корень.Скачать

Решите уравнение sin(πx/3) = 1/2 В ответе напишите наименьший положительный корень.

Лабораторная работа №1. Приближенное решение алгебраических и трансцендентных уравнений

Часть 2

Численные методы

Методические указания для самостоятельной работы студентов всех форм обучения

Составители: В.А. Бобкова,

Составители: В.А. Бобкова, Э.Г. Галиаскаров, В.А. Таланова

Сборник лабораторных работ по курсу «Информатика». Ч. 2. Численные методы: Методические указания для самостоятельной работы студентов всех форм обучения/ Сост.: В. А. Бобкова, Э.Г. Галиаскаров, В.А. Таланова. Иван. гос. хим.-технол. ун-т. – Иваново, 2002. 32 с.

Методические указания являются второй частью сборника лабораторных работ по курсу «Информатика». Они содержат индивидуальные задания для самостоятельных лабораторных работ по численным методам. В указаниях рассмотрены следующие темы: решение нелинейных уравнений и их систем; решение систем линейных уравнений; нахождение определенных интегралов численным методом; решение обыкновенных дифференциальных уравнений и их систем; решение дифференциальных уравнений в частных производных; математическая обработка экспериментальных данных; методы одномерной оптимизации; методы многомерной оптимизации; линейное программирование.

Методические указания предназначены для самостоятельной работы студентов технологических, механических и экономических специальностей вуза.

Библиогр.: 11 назв.

Рецензент доктор технических наук, профессор А. Н. Лабутин

(Ивановский государственный химико-технологический университет)

Введение

Основными целями лабораторного практикума по курсу «Информатика: Численные методы» являются:

— закрепление знаний по теоретическим основам использования численных методов для анализа математических моделей технических и экономических объектов;

— получение практических навыков работы на компьютерах, отладки и тестирования программ.

Методические указания являются второй частью сборника лабораторных работ по курсу «Информатика». Они содержат индивидуальные задания для самостоятельных лабораторных работ по численным методам. В указаниях рассмотрены следующие темы: решение нелинейных уравнений и их систем; решение систем линейных уравнений; нахождение определенных интегралов численным методом; решение обыкновенных дифференциальных уравнений и их систем; решение дифференциальных уравнений в частных производных; математическая обработка экспериментальных данных; методы одномерной оптимизации; методы многомерной оптимизации; линейное программирование.

Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до

Для реализации численных методов в процессе решения поставленных задач предполагается использование среды программирования Turbo Pascal, Borland Pascal. Решение ряда задач может быть дополнительно реализовано при использовании других программных пакетов, а именно MS Excel, MicroCal Origin.

Требования к оформлению лабораторных работ

Лабораторные работы оформляются в тетради в виде отчета, который должен содержать:

1. Название лабораторной работы.

3. Номер варианта и задание.

4. Расчетная часть:

a. Краткое теоретическое описание метода.

b. Блок-схема алгоритма метода.

c. Ручной расчет.

d. Текст программы.

Лабораторная работа №1. Приближенное решение алгебраических и трансцендентных уравнений

Задание:Локализовать наименьший положительный корень уравнения и уточнить его значение заданным методом с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до

№ вариантаУравнение№ вариантаУравнение
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до
Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до

Вопросы для самоподготовки

1. Что значит найти корень уравнения с точностью Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до?

2. Каковы этапы приближенного решения нелинейных уравнений? Какова цель каждого этапа?

3. Теорема о существовании и единственности корня на отрезке. Аналитическое и графическое отделение корней.

4. Метод половинного деления (алгоритм, геометрическая иллюстрация, условие окончания вычислений).

5. Метод хорд (алгоритм, геометрическая иллюстрация, условие окончания вычислений).

6. Метод касательных (условия применимости, алгоритм, геометрическая иллюстрация, условие окончания вычислений).

7. Комбинированный метод (условия применимости, алгоритм, геометрическая иллюстрация, условие окончания вычислений).

8. Метод итераций (алгоритм, геометрическая иллюстрация, условие окончания вычислений, достаточное условие сходимости итерационного процесса).

9. Сравнительная оценка методов уточнения корней.

Видео:Численное решение уравнений, урок 1/5. Локализация корняСкачать

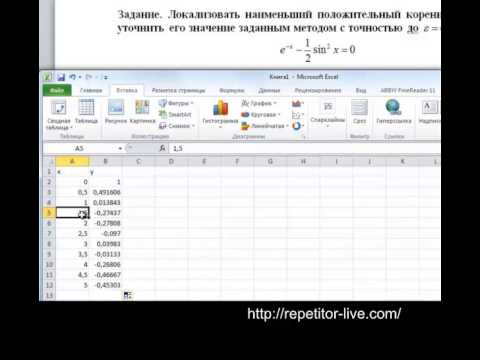
Численное решение уравнений, урок 1/5. Локализация корня

Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до

Локализовать наименьший положительный корень уравнения и уточнить его значение с точностью до

Вопросы для самоподготовки

1. Что значит найти корень уравнения с точностью ε ?

2. Каковы этапы приближенного решения нелинейных уравнений? Какова цель каждого этапа?

3. Теорема о существовании и единственности корня на отрезке. Аналитическое и графическое отделение корней.

4. Метод половинного деления (алгоритм, геометрическая иллюстрация, условие окончания вычислений).

5. Метод хорд (алгоритм, геометрическая иллюстрация, условие окончания вычислений).

6. Метод касательных (условия применимости, алгоритм, геометрическая иллюстрация, условие окончания вычислений).

7. Комбинированный метод (условия применимости, алгоритм, геометрическая иллюстрация, условие окончания вычислений).

8. Метод итераций (алгоритм, геометрическая иллюстрация, условие окончания вычислений, достаточное условие сходимости итерационного процесса).

9. Сравнительная оценка методов уточнения корней.

Видео:Найдите наименьший положительный корень уравнения sin pi x/3=-(корень из 3)/2 (проф. ЕГЭ задача №6)Скачать

Найдите наименьший положительный корень уравнения sin pi x/3=-(корень из 3)/2 (проф. ЕГЭ задача №6)

Численные методы решения нелинейных уравнений

В этом разделе приведены примеры решенных задач по теме нахождения корней нелинейных уравнений численными методами. На первом этапе обычно происходит локализация (отделение) корней (графически или аналитически), на втором — уточнение (поиск) корней разными методами: Ньютона, Стеффенсена, секущих, хорд, касательных, простой итерации.

Видео:sinπx/3=0,5 В ответе напишите наименьший положительный корень/ наибольший отрицательный кореньСкачать

sinπx/3=0,5 В ответе напишите наименьший положительный корень/ наибольший отрицательный корень

Примеры приближенных решений нелинейных уравнений онлайн

Задача 1. Методом бисекции найти решение нелинейного уравнения на отрезке $[a;b]$ с точностью $varepsilon = 10^$. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью $varepsilon=10^$. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.

Задача 2. Отделить корни нелинейного уравнения аналитически $2 arcctg x -x+3=0$.

Задача 3. Отделить корни нелинейного уравнения аналитически и уточнить один из них методом проб с точностью до 0,01. $$3x^4-8x^3-18x^2+2=0.$$

Задача 4. Отделить корни нелинейного уравнения графически (например, в среде EXCEL) уточнить один из них методом проб с точностью до 0,01. $$x^2-20 sin x =0.$$

Задача 5. Отделите корни уравнения графически и уточните один из них методом хорд с точностью до 0,001. Уточните один из корней этого уравнения методом касательных с точностью до 0,001. $$ sqrt — cos 0.387 x =0.$$

Задача 6.Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. $$sqrt=frac.$$

Задача 7. На отрезке $[0;2]$ методом Ньютона найти корень уравнения $-x^3-2x^2-4x+10=0$ с точностью 0,01.

Задача 8. Методом хорд найти отрицательный корень уравнения $x^3-2x^2-4x+7=0$ с точностью 0,0001. Требуется предварительное построение графика функции и отделение корней.

Задача 9. Решить нелинейные уравнения с точностью до 0.001. $$1), x^3-12x-5=0, (x gt 0), , 2), tan x -1/x=0. $$

📽️ Видео

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСС

Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод Ньютона (метод касательных) Пример Решения

Найти наименьший корень уравненияСкачать

Найти наименьший корень уравнения

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деления

Найти корень уравнения на заданном интервале (MathCad)Скачать

Найти корень уравнения на заданном интервале (MathCad)

Численное решение уравнений, урок 2/5. Метод деления отрезка пополамСкачать

Численное решение уравнений, урок 2/5. Метод деления отрезка пополам

ЕГЭ-2014 Задание В-7 Урок №112 Найти наименьший положительный корень тригонометрического уравненияСкачать

ЕГЭ-2014 Задание В-7 Урок №112 Найти наименьший положительный корень тригонометрического уравнения

Отбор корней по окружностиСкачать

Отбор корней по окружности

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnline

Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать

Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из Вебиума

Алгоритмы. Нахождение корней уравнения методом хордСкачать

Алгоритмы. Нахождение корней уравнения методом хорд

Решение нелинейного уравнения методом простых итераций (программа)Скачать

Решение нелинейного уравнения методом простых итераций (программа)

Численное решение уравнений, урок 3/5. Метод хордСкачать

Численное решение уравнений, урок 3/5. Метод хорд

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Три способа отбора корней в задании 13 ЕГЭ профиль

Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать

Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательных
Поделиться или сохранить к себе: