Инструкция . Введите выражение F(x) , нажмите Далее . Полученное решение сохраняется в файле Word . Также создается шаблон решения в Excel .
- Решение онлайн
- Видеоинструкция
- Оформление Word
Правила ввода функции, заданной в явном виде
- Примеры правильного написания F(x) :
- 10•x•e 2x = 10*x*exp(2*x)
- x•e -x +cos(3x) = x*exp(-x)+cos(3*x)
- x 3 -x 2 +3 = x^3-x^2+3
- Выражение 0.9*x=sin(x)+1 необходимо преобразовать к виду: sin(x)+1-0.9*x . Аналогично, x^2-7=5-3x к виду x^2+3x-12 .
Пусть дано уравнение f(x)=0 , где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b . Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x) . Число ξ называется корнем k -ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =f k-1 (ξ) = 0 . Однократный корень называется простым.
Приближенное нахождение корней уравнения складывается из двух этапов:- Отделение корней, то есть установление интервалов [αi,βi] , в которых содержится один корень уравнения.
- f(a)•f(b) , т.е. значения функции на его концах имеют противоположные знаки.
- f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).
- f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
- Уточнение приближенных корней, то есть доведение их до заданной точности.
Видео:5.1 Численные методы решения уравнений F(x)=0Скачать
Геометрическая интерпретация метода Ньютона (метод касательных)
Критерий завершения итерационного процесса имеет вид
Видео:Численное решение уравнений, урок 1/5. Локализация корняСкачать
Первый этап. Отделение корней
Отделить (локализовать) корни – это значит выделить из области допустимых значений функции y=f(x) отрезки, в каждом из которых содержится единственный корень.
Для функции общего вида не существует универсальных методов решения задачи локализации корней. Отделить корни уравнения f(x)=0 можно разными способами. Рассмотрим некоторые из них.
1) Табулирование функции. Строится таблица значений функции у=f(x) на некотором отрезке xÎ[a, b]. Если окажется, что для соседних значений аргумента значения функции имеют разные знаки, то хотя бы один корень уравнения 2.1 может находиться между ними.
2) Графический метод. Если удается построить график функции y=f(x), то можно определить количество и расположение нулей функции, выделяя те промежутки оси Х, где график y=f(x) пересекает ось Х.
Если построение графика y=f(x) затруднительно, тоисходное уравнение f(x)=0 заменяется эквивалентным ему уравнениемj(x)=y(x) и строятся графики функций у1=j(x) и у2=y(x). Искомый корень является абсциссой точки пересечения графиков этих функций.
3) Исходя из физического смысла задачи.
4) Убедиться в том, что на данном отрезке xÎ[a, b] (например, грубо определенном графическим способом) действительно имеется единственный корень уравнения (2.1), можно аналитическим способом, в основе которого лежит известная теорема математического анализа [3]:
Теорема 2.1. Если непрерывная на отрезке [a, b] функция y=f(x) принимает на концах его противоположные знаки, т.е. f(a)f(b) х – 2х 2 = 0, (2.2) т.е. выяснить, сколько корней имеет это уравнение, и найти интервалы, в которых находятся по единственному корню.
Способ1. Составим таблицу значений функции f(x)=4 – е х – 2х 2 на промежутке [–3, 1] (табулирование функции).
x -3 -2 -1 f(x)=4-е х -2х 2 –14,049 –4,135 1,632 3,012 –0,718 Из таблицы видно, что на отрезках [–2,–1] и [0,1] существуют, по крайней мере, по одному корню уравнения (2.2).
Способ2.Уравнение (2.2) эквивалентно уравнению j(x)=y(x), где. j (x)=4–2х 2 ; 3) y (x)= е х .
Построим графики функций у=j(x) и у=y(x) (рис. 2.2). Они пересекаются в двух точках, абсциссы которых х * 1 и х * 2 являются решениями уравнения j (x)=y (x), т.е. решением уравнения (2.2).
Рис. 2.2. Графический способ отделения корней
n Пример 2.2. Локализовать корни уравнения
которое получается при решении задачи устойчивости стержня (рис.2.3), где
При решении задач устойчивости нас обычно интересует наименьшее значение критической нагрузки, т.е. надо найти наименьший положительный корень уравнения (2.3).
Таблица 2.2
х
f(x)=х-tg(x) 0,000 0,5 –0,046 –0,557 1,5 –12,601 4,185 2,5 3,247 3,143 3,5 3,125 2,842 4,5 –0,137 Рис.2.3. К зада-че устойчи-вости стержня 5
Рис.2.4. Локализация корней уравнения х–tg(x)=0
Если при решении данной задачи отделение корней производить на основании таблицы табулирования (табл.2.2), то можно допустить ошибку, предположив, что корень уравнения находится на отрезке [1.5, 2], где функция меняет знак.
В действительности, на этом участке функция f(x)=х–tg(x) терпит разрыв (т.е. не выполняются условия теоремы 2.1) и это хорошо видно на рис.2.4.
Таким образом, искомый корень уравнения находится на отрезке [4, 4.5], где выполняются условия теоремы 2.1.
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать
Локализация и отделение корня
ЛЕКЦИЯ 3
Постановка задачи
Пусть требуется решить уравнение
.
Эта задача может быть решена точно лишь для очень узкого класса функций. Уже для многочленов степени выше четырех не существует формул, выражающих их корни через коэффициенты с помощью радикалов. Для большинства же уравнений, встречающихся в различных приложениях математики и технических задачах, приближенные методы решения являются единственно возможными.
Приближенно решить уравнение или вычислить корень уравнения
с заданной точностью
— это значит найти такое число
, для которого выполняется неравенство
, то есть указать на числовой прямой точку, лежащую на расстоянии не большем, чем допустимая погрешность, от точного значения корня.
Приближенное решение уравнения распадается на несколько задач:
·Локализация и отделение корня.
·Вычисление корня уравнения с заданной точностью
.
Локализация и отделение корня
Локализация корней ¾ необходимо определить количество, характер и расположение корней на числовой прямой. Все следующие задачи решаются для каждого корня в отдельности.
Отделение корня ¾ нужно указать отрезок
, внутри которого лежит один и только один корень данного уравнения.
Оба шага выполняются с помощью исследования функции методами математического анализа. Обычно строится схема графика функции и на основании первой теоремы Больцано–Коши и признака монотонности функции делается вывод.
Теорема 1. (Первая теорема Больцано–Коши) Если функция
непрерывна на отрезке
и на его концах принимает значения разного знака, т.е.
то на этом отрезке существует хотя бы одна точка, в которой функция обращается в ноль.
Теорема 2. Для того чтобы дифференцируемая на интервале
функция
возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы во всех его точках производная была неотрицательной
(неположительной)
.
Т.о. первая теорема обеспечивает существование корня на отрезке, а вторая его единственность.
Дано уравнение
. Отделить корень уравнения.
Перепишем уравнение в виде
и построим графики функций.
Из рисунка видно, что корень принадлежит отрезку
. Обоснуем это аналитически.
непрерывная.
,
по теореме 1.1 на отрезке существует корень.
на
, значит функция возрастает. Это обеспечивает единственность корня.
Метод половинного деления (бисекции)
Пусть имеется отрезок
, содержащий единственный корень уравнения
.
Ограничения. Никаких ограничений для функции нет.
Алгоритм. Обозначим отрезок
. Делим отрезок пополам точкой
. Если
, из двух получившихся отрезков
и
выбираем тот, который содержит корень уравнения, т.е. тот на концах которого, функция принимает значения разных знаков, его обозначим
. Этот новый отрезок
делим пополам и т.д. В результате получим последовательность вложенных отрезков
.
Теорема 3. Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем отрезкам этой последовательности.
Эта точка и есть корень уравнения.
Правило остановки. Процесс деления продолжается до тех пор, пока длина отрезка
не станем меньше
, действительно
, тогда в качестве
можно взять
или любую точку этого отрезка.
Середина
-го отрезка дает приближение к корню, имеющее оценку погрешности
. Это показывает, что метод сходится со скоростью геометрической прогрессии со знаменателем
. Это довольно медленно.
· Метод очень прост.
· Не имеет ограничений
· Если есть проблемы с отделением корня и в отрезке их несколько, то не понятно к какому сходимся.
· Метод не применим к корням четной кратности.
· Не обобщается на системы уравнений.
Вычислим корень уравнения
с точностью
.
-1 1,718 0,5 -0,101 1,718 0,5 0,5 0,75 -0,101 0,68 0,25 0,5 0,625 -0,101 0,259 0,125 0,5 0,563 -0,101 0,071 0,063 0,531 0,563 -0,016 0,071 0,032 0,531 0,547 -0,016 0,027 0,016 0,531 0,539 -0,016 0,005 0,008 Ограничения. Этот метод может быть использован только в том случае, если функция
на отрезке
не имеет точек перегиба, т.е.
постоянна по знаку.
Алгоритм. Через точки кривой
проведем хорду:
или после преобразований
.
По рисунку видно, что точка пересечения хорды с осью абсцисс лежит правее точки
, т.е. находится ближе к корню, для нее
,
т.е.
или
.
Эту точку будем считать первым приближением корня, т.е.
.
Теперь вместо отрезка
можно использовать
. При этом получим точку
и т.д.
Таким образом, получим последовательность значений
: если
, то
.
На следующем рисунке
, тогда
.
Теорема 4. Если функция
непрерывна и выпукла на отрезке
и
, то уравнение
имеет на отрезке единственный корень, и последовательность
монотонно сходится к нему.
Как видно, метод дает приближение к корню только с одной стороны и близость друг к другу последовательных приближений не обеспечивает близость к корню.
При выборе нулевого приближения следует руководствоваться рисунком или следующим правилом:
.
Если
, то вычисления можно прекратить, когда выполнено условие
. Это правило универсальное и может быть использовано для любого метода. Причем в силу выпуклости функции можно утверждать, что
.
Вычислим корень уравнения
с точностью
.
Ранее установлено, что корень принадлежит отрезку
.
,
для всех
.
Т.к.
,
возьмем
,
.
Будем использовать правило остановки 1, для этого вычислим
и
и возьмем
.
-1 0,368 -0,42 0,492 -0,122 0,526 -0,032 0,534 -0,008 Ограничения. Те же что и для метода хорд.
Алгоритм. Выберем
из условия
, т.е. конец отрезка противоположенный тому, который использовали в методе хорд.
Через точку
проведем касательную к функции
:
. Положив
, найдем точку пересечения касательной с осью абсцисс:
. Точка
находится к корню ближе, чем
. Продолжим построение касательных и вычисление последовательных приближений к корню по формуле
.
Для метода касательных также можно сформулировать теорему о сходимость этой последовательности к корню, аналогичную методу хорд.
Можно использовать правила из предыдущего метода.
Скорость сходимости. При выборе начального приближения из достаточно малой окрестности корня метод сходится квадратично, т.е. скорость сходимости велика. Для кратного корня скорость геометрической прогрессии.
Вычислим корень уравнения
с точностью
.
Возьмем
, т.к.
.
Будем использовать правило остановки 4, для этого вычислим
и
. Тогда
📽️ Видео
Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать
Метод половинного деления решение нелинейного уравненияСкачать
Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать
Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать
Найти корень уравнения на заданном интервале (MathCad)Скачать
Как найти корни уравнения в Excel с помощью Подбора параметраСкачать
ЧМ-1. Решение нелинейных уравнений. Часть 1/2Скачать
Информатика 2. S01.E08. Отделение корня уравненияСкачать
Метод половинного деления. ДихотомияСкачать
АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать
Численное решение уравнений, урок 2/5. Метод деления отрезка пополамСкачать
14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать
10 Численные методы решения нелинейных уравненийСкачать
Метод итерацийСкачать
СЛОЖИТЕ ДВА КОРНЯСкачать
15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать
🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать



 Таблица 2.2
Таблица 2.2 х
х
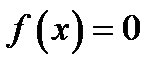 .
. с заданной точностью
с заданной точностью 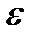 — это значит найти такое число
— это значит найти такое число 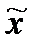 , для которого выполняется неравенство
, для которого выполняется неравенство 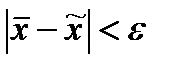 , то есть указать на числовой прямой точку, лежащую на расстоянии не большем, чем допустимая погрешность, от точного значения корня.
, то есть указать на числовой прямой точку, лежащую на расстоянии не большем, чем допустимая погрешность, от точного значения корня. , внутри которого лежит один и только один корень данного уравнения.
, внутри которого лежит один и только один корень данного уравнения. непрерывна на отрезке
непрерывна на отрезке 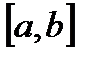 и на его концах принимает значения разного знака, т.е.
и на его концах принимает значения разного знака, т.е.  то на этом отрезке существует хотя бы одна точка, в которой функция обращается в ноль.
то на этом отрезке существует хотя бы одна точка, в которой функция обращается в ноль.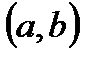 функция
функция  возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы во всех его точках производная была неотрицательной
возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы во всех его точках производная была неотрицательной  (неположительной)
(неположительной)  .
.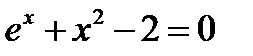 . Отделить корень уравнения.
. Отделить корень уравнения.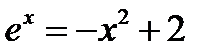 и построим графики функций.
и построим графики функций.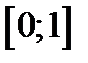 . Обоснуем это аналитически.
. Обоснуем это аналитически. непрерывная.
непрерывная.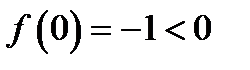 ,
,  по теореме 1.1 на отрезке существует корень.
по теореме 1.1 на отрезке существует корень. на
на 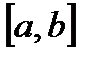 , содержащий единственный корень уравнения
, содержащий единственный корень уравнения  .
. . Делим отрезок пополам точкой
. Делим отрезок пополам точкой 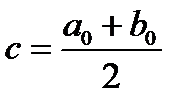 . Если
. Если 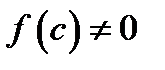 , из двух получившихся отрезков
, из двух получившихся отрезков 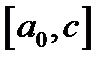 и
и  выбираем тот, который содержит корень уравнения, т.е. тот на концах которого, функция принимает значения разных знаков, его обозначим
выбираем тот, который содержит корень уравнения, т.е. тот на концах которого, функция принимает значения разных знаков, его обозначим  . Этот новый отрезок
. Этот новый отрезок 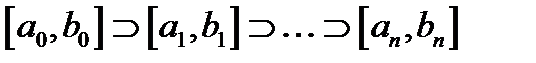 .
. не станем меньше
не станем меньше  , тогда в качестве
, тогда в качестве  можно взять
можно взять 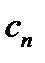 или любую точку этого отрезка.
или любую точку этого отрезка.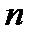 -го отрезка дает приближение к корню, имеющее оценку погрешности
-го отрезка дает приближение к корню, имеющее оценку погрешности 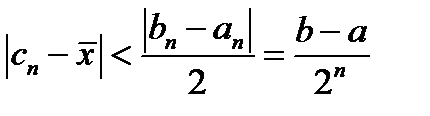 . Это показывает, что метод сходится со скоростью геометрической прогрессии со знаменателем
. Это показывает, что метод сходится со скоростью геометрической прогрессии со знаменателем 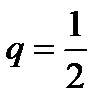 . Это довольно медленно.
. Это довольно медленно.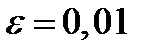 .
.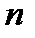
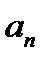


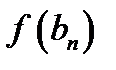
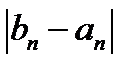
 на отрезке
на отрезке 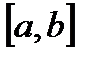 не имеет точек перегиба, т.е.
не имеет точек перегиба, т.е. 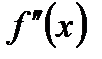 постоянна по знаку.
постоянна по знаку.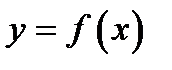
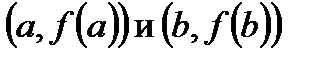 проведем хорду:
проведем хорду: 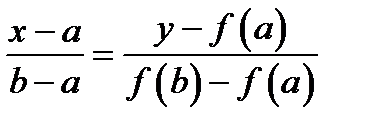 или после преобразований
или после преобразований 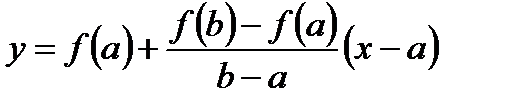 .
.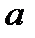 , т.е. находится ближе к корню, для нее
, т.е. находится ближе к корню, для нее 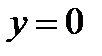 ,
,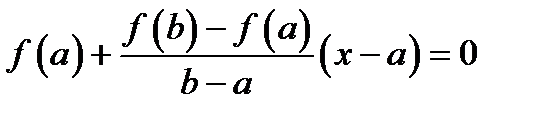
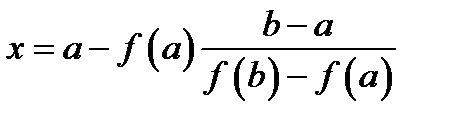 .
.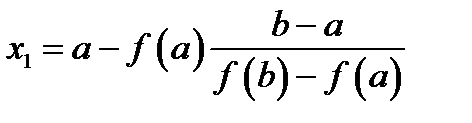 .
.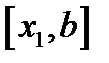 . При этом получим точку
. При этом получим точку 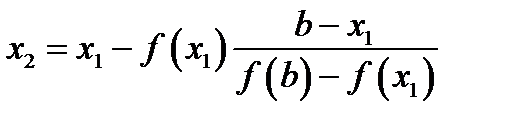 и т.д.
и т.д. : если
: если 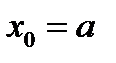 , то
, то 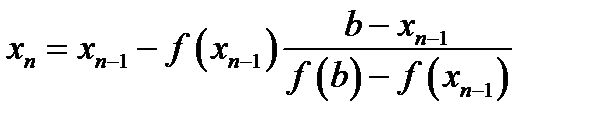 .
.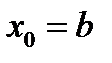 , тогда
, тогда  .
. , то уравнение
, то уравнение  .
. , то вычисления можно прекратить, когда выполнено условие
, то вычисления можно прекратить, когда выполнено условие  . Это правило универсальное и может быть использовано для любого метода. Причем в силу выпуклости функции можно утверждать, что
. Это правило универсальное и может быть использовано для любого метода. Причем в силу выпуклости функции можно утверждать, что 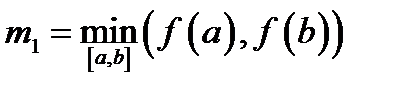 .
.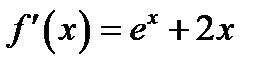 ,
, 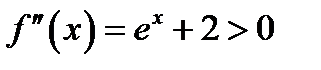 для всех
для всех  .
.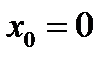 ,
, 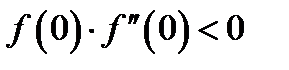 .
.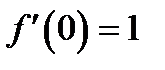 и
и  и возьмем
и возьмем  .
.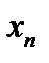

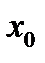 из условия
из условия  , т.е. конец отрезка противоположенный тому, который использовали в методе хорд.
, т.е. конец отрезка противоположенный тому, который использовали в методе хорд.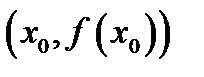 проведем касательную к функции
проведем касательную к функции 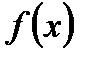 :
:  . Положив
. Положив 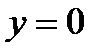 , найдем точку пересечения касательной с осью абсцисс:
, найдем точку пересечения касательной с осью абсцисс:  . Точка
. Точка 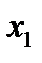 находится к корню ближе, чем
находится к корню ближе, чем  .
. , т.к.
, т.к.  .
. . Тогда
. Тогда 
















