- 1.1 Область локализации корней
- 1.2 Критерии сходимости при решении уравнений
- 1.3 Метод половинного деления (метод дихотомии)
- Пример решения уравнения методом дихотомии
- 2 Решение уравнений , используя “Подбор параметра ”
- 2.1 Пример решения уравнения, используя “Подбор параметра”
- 3 Решение уравнений и систем уравнений, используя надстройку “Поиск решения”
- 3.1 Пример решения уравнения, используя надстройку “Поиск решения”
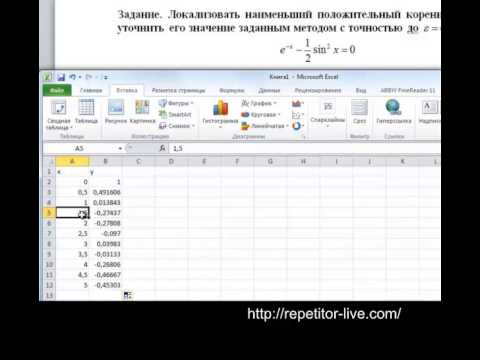
- Задание 1. Решение уравнений численным методом
- Задания 2. Решение уравнений встроенными средствами “Подбор параметра” и “Поиск решения”
- Локализация и отделение корня
- Отделение корней В Excel
- Лабораторная работа
- Отделение корней нелинейного уравнения
- Аналитический способ отделения корней
- 📹 Видео
Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

1.1 Область локализации корней
В общем виде любое уравнение одной переменной принято записывать так 

Например , для уравнения 

Рисунок 1. График функции 
Таким образом, можно приблизительно определять область локализации корней уравнения. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён.
Некоторые виды уравнений допускают аналитическое решение. Например, степенные алгебраические уравнения степени n 

Видео:Численное решение уравнений, урок 1/5. Локализация корняСкачать
1.2 Критерии сходимости при решении уравнений
Ø Абсолютная погрешность — абсолютное изменение приближения на соседних шагах итерации
Ø Относительная погрешность — относительное изменение приближения на соседних шагах итерации
Ø Близость к нулю вычисленного значения левой части уравнения (иногда это значение называют невязкой уравнения, так как для корня невязка равна нулю)
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

1.3 Метод половинного деления (метод дихотомии)
Метод половинного деления основан на последовательном делении отрезка локализации корня пополам.
Для этого выбирается начальное приближение к отрезку [ a , b ], такое, что f ( a ) × f ( b ) 
Рисунок 2. Последовательное деление отрезка пополам и приближение к корню
Алгоритм метода дихотомии можно записать так:
1. представить решаемое уравнение в виде
2. выбрать a, b и вычислить
3. если f(a) × f( с ) то a=a; b = c иначе a = c; b=b
4. если критерий сходимости не выполнен, то перейти к п. 2
Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Пример решения уравнения методом дихотомии
Найти решение заданного уравнения методом дихотомии с точностью до 10 -5 .
Пример создания расчетной схемы на основе метода дихотомии на примере уравнения: 
Данный метод заключается в проверке на каждой итерации условия:
если f ( a ) × f (с) 
Рисунок 3. Последовательность итераций метода дихотомии при поиске корня уравнения 
a ) схема расчета (зависимые ячейки); b) режим отображения формул;
Для нашего примера итерационная последовательность для нахождения решения принимает вид:
Точность до пятой значащей цифры достигается за 20 итераций.
Скорость сходимости этого метода является линейной.
При выполнении начального условия он сходится к решению всегда.
Метод половинного деления удобен при решении физически реальных уравнений, когда заранее известен отрезок локализации решения уравнения.
Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

2 Решение уравнений , используя “Подбор параметра ”
Используя возможности Excel можно находить корни нелинейного уравнения вида f(x)=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:
1. Производится табулирование функции в диапазоне вероятного существования корней;
2. По таблице фиксируются ближайшие приближения к значениям корней;
3. Используя средство Excel Подбор параметра, вычисляются корни уравнения с заданной точностью.
При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка П родолжить — для возврата в обычный режим подбора параметра.
Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

2.1 Пример решения уравнения, используя “Подбор параметра”
Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3].
Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3; 3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня.
Рисунок 4. Поиск приближенных значений корней уравнения
Выполните команду меню Сервис/Параметры, во вкладке Вычисления установите относительную погрешность вычислений E=0,00001, а число итераций N=1000, установите флажок Итерации.
Выполните команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 9) заполните следующие поля:
þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;
þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);
þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.
Рисунок 5. Диалоговое окно Подбор параметра для поиска первого корня
После щелчка на ОК получим значение первого корня -1,65793685 .
Выполняя последовательно операции аналогичные предыдущим, вычислим значения остальных корней: -0,35913476 и 2,05170101 .
Видео:Найти корень уравнения на заданном интервале (MathCad)Скачать

3 Решение уравнений и систем уравнений, используя надстройку “Поиск решения”
Для решения уравнений можно также использовать команду Поиск решения, доступ к которой реализуется через пункт меню Сервис/Поиск решения.
Последовательность операций нахождения корней следующая:
1. Найти приближенное значение корня уравнения
2. Открыть диалог Поиск решения и установить следующие параметры (рисунок 10):
þ в поле У становить целевую ячейку ввести адрес ячейки, содержащей формулу (левую часть уравнения);
þ установить переключатель в положение ‘ значению’ и ввести значение 0 (правая часть уравнения);
þ в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргумента x целевой функции,;
þ в поле Ограничения с помощью кнопки Д обавить ввести все ограничения, которым должен отвечать результат поиска (область поиска корня уравнения);
þ для запуска процесса поиска решения нажать кнопку В ыполнить.
þ Для сохранения полученного решения необходимо использовать переключатель С охранить найденное решение в открывшемся окне диалога Результаты поиска решения.

Рисунок 6. Диалоговое окно Поиск решения
Полученное решение зависит от выбора начального приближения. Поиск начальных приближений рассмотрен выше.
Рассмотрим некоторые Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения):
þ Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).
þ Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).
þ Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.
þ Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.
þ Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и если итерации дают слишком малое отличие в последовательных приближениях.
Рисунок 7. Вкладка Параметры окна Поиск решения
Видео:Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

3.1 Пример решения уравнения, используя надстройку “Поиск решения”
Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3]. Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3;3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня. На рисунке 12 представлен пример заполнения окна Поиск решения для нахождения первого корня на отрезке [-2; -1].
Рисунок 8. Пример решения уравнения при помощи надстройки Поиск решения
Видео:8 класс, 21 урок, Графическое решение уравненийСкачать

Задание 1. Решение уравнений численным методом
На листе 1 (название листа: Численные методы) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания ) реализовать итерационные расчетные схемы методов, указанных в Таблице 1 для нахождения хотя бы одного корня на заданном интервале. Количество итераций просчитать, оценивая 

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Задания 2. Решение уравнений встроенными средствами “Подбор параметра” и “Поиск решения”
На листе 2 (название листа: Подбор Поиск) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания) на заданном интервале и с некоторым шагом (шаг выбрать самостоятельно) построить таблицу значений функции f(x) и определить количество корней уравнения и выделить интервалы, на которых находятся корни. Построить график функции. Уточнить на заданных интервалах с точностью до 10 -6 корни уравнения с помощью встроенных средств: Подбор параметра, Поиск решения
Видео:Информатика 2. S01.E08. Отделение корня уравненияСкачать

Локализация и отделение корня
ЛЕКЦИЯ 3
Постановка задачи
Пусть требуется решить уравнение 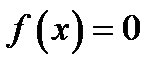
Эта задача может быть решена точно лишь для очень узкого класса функций. Уже для многочленов степени выше четырех не существует формул, выражающих их корни через коэффициенты с помощью радикалов. Для большинства же уравнений, встречающихся в различных приложениях математики и технических задачах, приближенные методы решения являются единственно возможными.
Приближенно решить уравнение или вычислить корень уравнения 
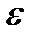
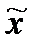
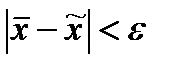
Приближенное решение уравнения распадается на несколько задач:
·Локализация и отделение корня.
·Вычисление корня уравнения с заданной точностью 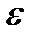
Локализация и отделение корня
Локализация корней ¾ необходимо определить количество, характер и расположение корней на числовой прямой. Все следующие задачи решаются для каждого корня в отдельности.
Отделение корня ¾ нужно указать отрезок 
Оба шага выполняются с помощью исследования функции методами математического анализа. Обычно строится схема графика функции и на основании первой теоремы Больцано–Коши и признака монотонности функции делается вывод.
Теорема 1. (Первая теорема Больцано–Коши) Если функция 
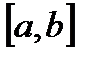

Теорема 2. Для того чтобы дифференцируемая на интервале 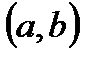



Т.о. первая теорема обеспечивает существование корня на отрезке, а вторая его единственность.
Дано уравнение 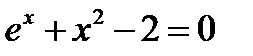
Перепишем уравнение в виде 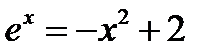
Из рисунка видно, что корень принадлежит отрезку 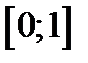



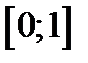
Метод половинного деления (бисекции)
Пусть имеется отрезок 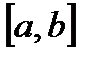

Ограничения. Никаких ограничений для функции нет.
Алгоритм. Обозначим отрезок 
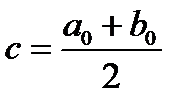
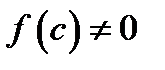
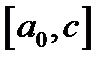



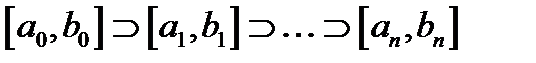
Теорема 3. Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем отрезкам этой последовательности.
Эта точка и есть корень уравнения.
Правило остановки. Процесс деления продолжается до тех пор, пока длина отрезка 
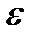


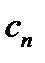
Середина 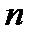
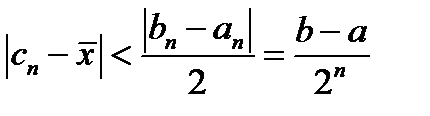
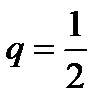
· Метод очень прост.
· Не имеет ограничений
· Если есть проблемы с отделением корня и в отрезке их несколько, то не понятно к какому сходимся.
· Метод не применим к корням четной кратности.
· Не обобщается на системы уравнений.
Вычислим корень уравнения 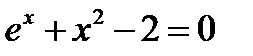
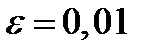
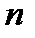 | 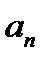 |  |  | 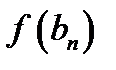 | 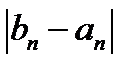 | |||||||||||
| -1 | 1,718 | |||||||||||||||
| 0,5 | -0,101 | 1,718 | 0,5 | |||||||||||||
| 0,5 | 0,75 | -0,101 | 0,68 | 0,25 | ||||||||||||
| 0,5 | 0,625 | -0,101 | 0,259 | 0,125 | ||||||||||||
| 0,5 | 0,563 | -0,101 | 0,071 | 0,063 | ||||||||||||
| 0,531 | 0,563 | -0,016 | 0,071 | 0,032 | ||||||||||||
| 0,531 | 0,547 | -0,016 | 0,027 | 0,016 | ||||||||||||
| 0,531 | 0,539 | -0,016 | 0,005 | 0,008 Ограничения. Этот метод может быть использован только в том случае, если функция Алгоритм. Через точки кривой По рисунку видно, что точка пересечения хорды с осью абсцисс лежит правее точки т.е. или Эту точку будем считать первым приближением корня, т.е. Теперь вместо отрезка Таким образом, получим последовательность значений На следующем рисунке Теорема 4. Если функция Как видно, метод дает приближение к корню только с одной стороны и близость друг к другу последовательных приближений не обеспечивает близость к корню. При выборе нулевого приближения следует руководствоваться рисунком или следующим правилом: Если Вычислим корень уравнения Ранее установлено, что корень принадлежит отрезку Т.к. Будем использовать правило остановки 1, для этого вычислим
|













 на отрезке
на отрезке 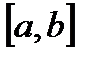 не имеет точек перегиба, т.е.
не имеет точек перегиба, т.е. 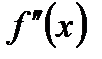 постоянна по знаку.
постоянна по знаку.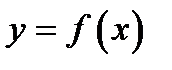
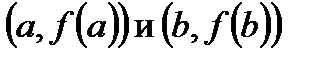 проведем хорду:
проведем хорду: 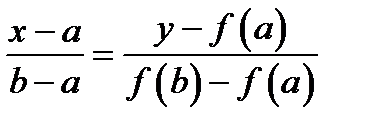 или после преобразований
или после преобразований 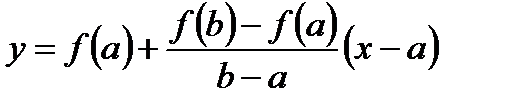 .
.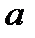 , т.е. находится ближе к корню, для нее
, т.е. находится ближе к корню, для нее 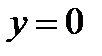 ,
,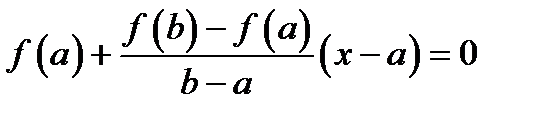
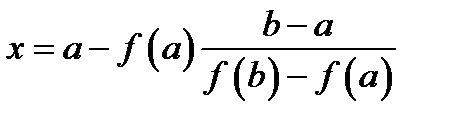 .
.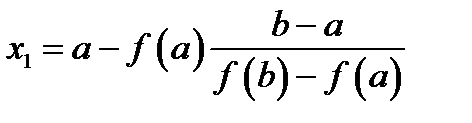 .
.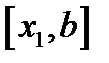 . При этом получим точку
. При этом получим точку 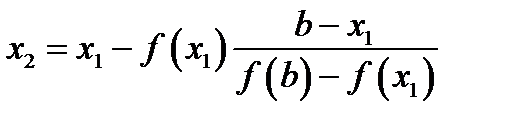 и т.д.
и т.д. : если
: если 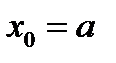 , то
, то 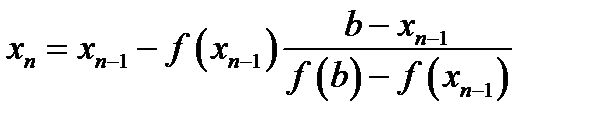 .
.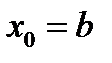 , тогда
, тогда  .
. , то уравнение
, то уравнение  .
. , то вычисления можно прекратить, когда выполнено условие
, то вычисления можно прекратить, когда выполнено условие  . Это правило универсальное и может быть использовано для любого метода. Причем в силу выпуклости функции можно утверждать, что
. Это правило универсальное и может быть использовано для любого метода. Причем в силу выпуклости функции можно утверждать, что 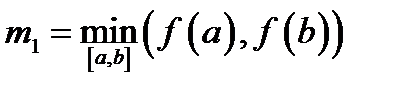 .
.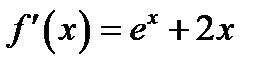 ,
, 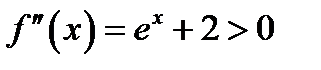 для всех
для всех  .
.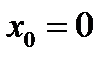 ,
, 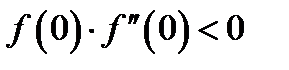 .
.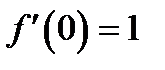 и
и  и возьмем
и возьмем  .
.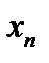

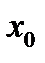 из условия
из условия  , т.е. конец отрезка противоположенный тому, который использовали в методе хорд.
, т.е. конец отрезка противоположенный тому, который использовали в методе хорд.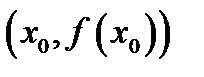 проведем касательную к функции
проведем касательную к функции 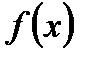 :
:  . Положив
. Положив 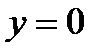 , найдем точку пересечения касательной с осью абсцисс:
, найдем точку пересечения касательной с осью абсцисс:  . Точка
. Точка 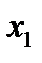 находится к корню ближе, чем
находится к корню ближе, чем  .
. , т.к.
, т.к.  .
. . Тогда
. Тогда 



 .
. , где содержится один и только один корень уравнения. Одна из точек этого промежутка принимается за начальное приближение корня. В зависимости от метода, который предполагается использовать для уточнения корня, требуется определение некоторых свойств отделенного корня и поведения функции на отрезке отделения. Например, при использовании метода деления пополам, необходимо и достаточно установить лишь непрерывность функции на отрезке отделения.
, где содержится один и только один корень уравнения. Одна из точек этого промежутка принимается за начальное приближение корня. В зависимости от метода, который предполагается использовать для уточнения корня, требуется определение некоторых свойств отделенного корня и поведения функции на отрезке отделения. Например, при использовании метода деления пополам, необходимо и достаточно установить лишь непрерывность функции на отрезке отделения. . Часто применяется графический метод отделения действительных корней, обладающий большой наглядностью.
. Часто применяется графический метод отделения действительных корней, обладающий большой наглядностью.


 функция
функция  , то на этом отрезке содержится, по крайней мере, один корень уравнения. Если же функция
, то на этом отрезке содержится, по крайней мере, один корень уравнения. Если же функция 








