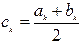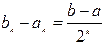Локализация корней уравнения метод ньютона

Инструкция . Введите выражение F(x) , нажмите Далее . Полученное решение сохраняется в файле Word . Также создается шаблон решения в Excel .

• Решение онлайн
• Видеоинструкция
• Оформление Word

Правила ввода функции, заданной в явном виде

2. Примеры правильного написания F(x) :
   1. 10•x•e 2x = 10*x*exp(2*x)
   2. x•e -x +cos(3x) = x*exp(-x)+cos(3*x)
   3. x 3 -x 2 +3 = x^3-x^2+3
   4. Выражение 0.9*x=sin(x)+1 необходимо преобразовать к виду: sin(x)+1-0.9*x . Аналогично, x^2-7=5-3x к виду x^2+3x-12 .

   Пусть дано уравнение f(x)=0 , где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b . Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x) . Число ξ называется корнем k -ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =f k-1 (ξ) = 0 . Однократный корень называется простым.
   Приближенное нахождение корней уравнения складывается из двух этапов:

   1. Отделение корней, то есть установление интервалов [α_i,β_i] , в которых содержится один корень уравнения.
      1. f(a)•f(b) , т.е. значения функции на его концах имеют противоположные знаки.
      2. f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).
      3. f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
   2. Уточнение приближенных корней, то есть доведение их до заданной точности.

   Видео:Метод касательных (метод Ньютона)Скачать

   

   Геометрическая интерпретация метода Ньютона (метод касательных)

   Критерий завершения итерационного процесса имеет вид

   Видео:Метод Ньютона - отделение корнейСкачать

   

   Метод Ньютона

   Этот онлайн калькулятор ищет корень (нуль) заданной функции, используя метод Ньютона (также известный как метод касательных)

   Этот онлайн калькулятор применяет метод Ньютона (также известный как метод касательных) используя калькулятор производных для получения аналитической формулы производной заданной функции (метод Ньютона требует вычисления производной). Под калькулятором можно прочитать краткое описание метода.

   

   Метод Ньютона

   Метод Ньютона 1

   Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.

   Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. Далее процесс повторяется, пока не будет достигнута необходимая точность.

   Уравнение касательной к графику функции выглядит следующим образом:
   ,
   где — тангенс угла пересечения касательной с осью абсцисс.

   Тангенс угла пересечения касательной с осью абсцисс, — не что иное, как значение производной в точке .
   С учетом того факта, что в точке пересечения с осью абсцисс значение y равно нулю, можно записать следующее выражение для нахождения точки пересечения (следующей точки приближения):

   Метод Ньютона является очень мощным методом поиска корней функции, так как имеет квадратичную скорость сходимости — количество значащих цифр примерно удваивается с каждым шагом итерации, однако существуют и ограничения, затрудняющие его применение. Так, например, если начальное приближение недостаточно близко к решению, то метод может не сойтись, если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня, если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена, если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

   Теорема Канторовича дает следующие условия применимости метода для поиска корней функции:

   1. функция должна быть ограничена;
   2. функция должна быть гладкой, дважды дифференцируемой;
   3. её первая производная f'(x) равномерно отделена от нуля;
   4. её вторая производная f»(x) должна быть равномерно ограничена.

   Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

   

   Метод Ньютона (метод касательных)

   Lesson 6

   Численные методы

   На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит потому, что искомое решение обычно не выражается в элементарных или других известных функциях. Поэтому большое значение приобрели численные методы.

   Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами. В зависимости от сложности задачи, заданной точности, применяемого метода может потребоваться огромное количество действий, и здесь без быстродействующего компьютера не обойтись.

   Решение, полученное численным методом, обычно является приближенным, т. е. содержит некоторую погрешность. Источниками погрешности приближенного решения задачи являются:

   — погрешность метода решения;

   — погрешности округлений в действиях над числами.

   Погрешность метода вызвана тем, что численным методом обычно решается другая, более простая задача, аппроксимирующая (приближающая) исходную задачу. В ряде случаев численный метод представляет собой бесконечный процесс, который в пределе приводит к искомому решению. Процесс, прерванный на некотором шаге, дает приближенное решение.

   Погрешность округления зависит от количества арифметических действий, выполняемых в процессе решения задачи. Для решения одной и той же задачи могут применяться различные численные методы. Чувствительность к погрешностям округления существенно зависит от выбранного метода.

   Решение нелинейных уравнений

   Постановка задачи

   Решение нелинейных уравнений с одним неизвестным является одной из важных математических задач, возникающих в различных разделах физики, химии, биологии и других областях науки и техники.

   В общем случае нелинейное уравнение с одним неизвестным можно записать:

   где f ( x) – некоторая непрерывная функция аргумента x.

   Всякое число x₀ , при котором f (x₀) ≡ 0, называется корнем уравнения f ( x) = 0.

   Методы решения нелинейных уравнений делятся на прямые (аналитические, точные) и итерационные. Прямые методы позволяют записать решение в виде некоторого соотношения (формулы). При этом значения корней могут быть вычислены по этой формуле за конечное число арифметических операций. Подобные методы развиты для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

   Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. Даже для алгебраического уравнения выше четвертой степени не удается получить аналитического решения в виде формулы с конечным числом арифметических действий. Во всех таких случаях приходится обращаться к численным методам, позволяющим получить приближенные значения корней с любой заданной точностью.

   При численном подходе задача о решении нелинейных уравнений разбивается на два этапа: локализация (отделение) корней, т.е. нахождение таких отрезков на оси x, в пределах которых содержится один единственный корень, и уточнение корней, т.е. вычисление приближенных значений корней с заданной точностью.

   Локализация корней

   Для отделения корней уравнения f ( x) = 0 необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке [ a, b] имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке.

   Если функция f ( x) непрерывна на отрезке [ a, b], а на концах отрезка её значения имеют разные знаки, т. е.

   Воспользовавшись этим критерием, можно отделить корни аналитическим способом, находя интервалы монотонности функции.

   Отделение корней можно выполнить графически, если удается построить график функции y = f ( x) . Например, график функции на рисунке (1) показывает, что эта функция на интервале [a, b] может быть разбита на три интервала монотонности и на этом интервале у нее существуют три корня.

   Отделение корней можно также выполнить табличным способом. Допустим, что все интересующие нас корни уравнения (2.1) находятся на отрезке [A, B]. Выбор этого отрезка (интервала поиска корней) может быть сделан, например, на основе анализа конкретной физической или иной задачи.

   

   Рис. 2. Табличный способ локализации корней.

   Будем вычислять значения f ( x) , начиная с точки x = A , двигаясь вправо с некоторым шагом h (рис. 2). Как только обнаруживается пара соседних значений f ( x) , имеющих разные знаки, так соответствующие значения аргумента x можно считать границами отрезка, содержащего корень.

   Надежность табличного способа отделения корней уравнений зависит как от характера функции f ( x) , так и от выбранной величины шага h. Действительно, если при достаточно малом значении h ( h

   должно отличаться от точного x₀ не более чем на величину ε:

   Процедура численного определения приближенных значений корней нелинейных уравнений, как правило, состоит в выборе начального приближения к корню x₀ Î[ a, b] и вычислении по некоторой формуле последующих приближений , x₁ x₂ и т.д. Каждый такой шаг называется итерацией, а сами методы уточнения – итерационными методами. В результате итераций получается последовательность приближенных значений корня
   x₀ , x₁ , . . . , x_k, . . . , которая называется итерационной последовательностью. Если эти значения с ростом k стремятся к точному значению корня x₀, то говорят, что итерационный процесс сходится :

   

   Методы уточнения корней

   Метод половинного деления

   Считаем, что отделение корней уравнения f ( x) = 0 проведено и на отрезке [ a, b] расположен один корень, который необходимо уточнить с погрешностью ε. В качестве начального приближения корня принимаем середину этого отрезка: c₀ = (a + b) / 2 (рис. 4):

   

   Рис. 4. Метод половинного деления.

   Затем исследуем значение функции f ( x) на концах отрезков [ a, c₀ ] и [ c₀ , b] . Тот из отрезков, на концах которого f ( x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка [ a₁ , b₁ ] (на рис. 4 это отрезок [ a, c₀ ]). Вторую половину отрезка [ a, b], на которой f ( x) не меняет знак, отбрасываем. В качестве следующего приближения корня принимаем середину нового отрезка
   c₁ = ( a₁ + b₁ ) / 2 и т.д. Таким образом, k-е приближение вычисляется как

   

   После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k итераций в 2 k раз:

   

   Прекратить итерационный процесс следует, когда будет достигнута заданная точность, т.е. при выполнении условия |x₀ – c_k|

   🔍 Видео

   15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

   

   Численный метод Ньютона в ExcelСкачать

   

   Метод Ньютона, или Извлечение квадратного корняСкачать

   

   Метод Ньютона (Метод касательных)Скачать

   

   МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

   

   Численное решение уравнений, урок 1/5. Локализация корняСкачать

   

   Алгоритмы. Нахождение корней уравнения методом хордСкачать

   

   Метод Касательных - ВизуализацияСкачать

   

   Вычислительная математика. Метод касательных на Python(1 практика).Скачать

   

   Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

   

   Численное решение уравнений, урок 4/5. Метод касательных (Ньютона)Скачать

   

   Методы решения систем нелинейных уравнений. Метод Ньютона. Численные методы. Лекция 14Скачать

   

   Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

   

   11 Метод Ньютона (Метод касательных) Mathcad Численные методы решения нелинейного уравненияСкачать

   

   Метод Ньютона для решения нелинйеных уравнений в MS ExcelСкачать

   

   Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

   

   10 Метод Ньютона (Метод касательных) C++ Численные методы решения нелинейного уравненияСкачать