Математическая модель, описывающая процессы, подобные развитию эпидемии называется уравнением Ферхюльста, или логистическим уравнением. Уравнение описывает увеличение некоторой популяции в присутствии ограничения ее максимума. Популяция (например, количество заболевших) в начале эпидемии увеличивается экспоненциально, но количество заболевших ограничено численностью населения и постепенно рост замедляется. Кривая, иллюстрирующая этот процесс называется логистической.
К сожалению, статистические данные о заболеваемости и смертности неоднородны и не всегда достоверны. Это связано с разным развитием медицины по странам и отсутствием общих стандартов в том, кто является заболевшим и, даже, причины смерти. Например, в Италии, если скончался зараженный человек, то в статистике определяется смерть от коронавируса. А в Германии (и в России) чаще диагностируют смерть от обострившегося хронического заболевания. Поэтому в Италии смертность (4032/47021) = 8.6%, а в Германии всего (45/18323) = 0.25% от количества заболевших. В каких-то странах проводят массовое тестирование жителей и включают в статистику даже бессимптомных вирусоносителей, в других странах диагностируют только тяжелых больных, да и то не всегда.
Графики официальной статистики по странам можно изучить на сайтах https://observablehq.com/@elaval/coronavirus-worldwide-evolution
http://shinyapps.org/apps/corona/
Хорошую статистику дает паром Diamond Princess.
3500 человек на борту (большинство — пенсионеры).
712 заразившихся, из них 362 бессимптомно.
7 смертных случаев.
Почему 80% не заразилось, неизвестно. Возможно, некоторые люди этой инфекцией совсем не заражаются, но это не точно…
Из выступления Генерального директора ВОЗ от 17.02.2020.
«У более 80% пациентов болезнь протекает в легкой форме и заканчивается полным выздоровлением.
Примерно в 14% случаев течение болезни тяжелое и сопровождается, в частности, пневмонией и одышкой.
И, наконец, у порядка 5% пациентов развивается опасное для жизни заболевание, сопровождающееся такими проявлениями, как респираторная недостаточность, септический шок и полиорганная недостаточность.
В 2% случаев заражение вирусом приводит к смерти, причем этот риск возрастает пропорционально возрасту пациента. „
Возможно, что Гендиректор ВОЗ совсем не учел бессимптомных инфицированных, поэтому делим все пополам.
Итак, на 100% инфицированных:
90% бессимптомно, или в легкой форме;
10% — требуется госпитализация, из них:
2.5% — тяжелые, требуется реанимация (наверное, искусственная вентиляция легких?);
1% — смертность.
Точное решение логистического уравнения:
N=M*EXP(r*t)/(1+EXP(r*t)); где
N — размер популяции в момент t;
M — максимальный размер популяции;
r — скорость роста популяции, увеличение за день (проценты/100);
t — текущее время в днях, отсчитывается от середины логистической кривой.
Для определения времени:
t=(1/r)*LN(N/(M-N));
Простота использования логистического уравнения заключается в том, что для его решения нужно всего 2 параметра — максимальный размер популяции и скорость ее роста.
Для примера посчитаем смертность в Италии. Население Италии — 60 млн. человек. Будем считать, что вирусом заразятся половина населения, 30 млн. Увы, 1%, 300 тыс. из них могут погибнуть. В настоящее время умерло 4032 человека, скорость роста процесса — 15% в день. Число заболевших в Италии в начале эпидемии увеличивалось на 25% в день, сейчас, при карантине, 13%. Смертность отстает от количества заболевших, умирают через 11 дней после заражения, так что считаем, что и смертность упадет до 13%.
r=0.13; N=4032; M=300000.
Ответ пугает. t=33. Через 33 дня в Италии могут умереть от вируса 150 тысяч человек. В это время будут умирать до 9700 человек в день.
Если бы карантина не было, скорость распространения осталась бы 25%, максимум был бы достигнут на 17 день, ежедневная смертность в максимуме — 18650 человек. Карантин сдвигает процесс и уменьшает максимум. Справится ли итальянская медицина?
Но вместо закрытия промышленности, вместо полного карантина есть более элегантное решение.
По данным Высшего института здоровья Италии почти 90% умерших в Италии старше 70 лет. 
При r=0.2; M=30000, максимум будет достигнут через 28 дней. Максимальное количество новых смертей в день — 1495. 
Если также изолировать и более молодых с опасными заболеваниями, количество смертей можно еще уменьшить. Наиболее распространенные хронические патологии у умерших:
ишемическая кардиопатия — 37,3%
мерцательная аритмия — 26.5%
перенесенный инсульт — 8,2%
артериальная гипертензия — 76,5%
сахарный диабет — 37,3%
деменция — 4,5%
хроническая обструктивная болезнь легких — 9,7%
рак, активный в течение последних 5 лет — 19,4%
хроническая гепатопатия — 7%
хроническая почечная недостаточность — 17,5%
Количество заболевших коронавирусом в России увеличивается более чем на 25% ежедневно. Это означает в 10 раз за 10 дней, в 1000 раз за месяц. С такими темпами через месяц у нас будут сотни тысяч больных. Самые строгие карантинные мероприятия смогут снизить темпы ежедневного роста заболеваемости вдвое, до 13% (на примере Италии). Карантинные меры обрушивают экономику и не достигают поставленной задачи — снизить нагрузку на медицину до приемлемого уровня.
Между тем, имеется эффективное решение проблемы.
90% тяжелых больных и смертельных исходов наблюдается у лиц, старше 70 лет. Строгий карантин для пожилых людей и хронических больных. Для этого надо задействовать пансионаты и дома отдыха. Установить строгий режим, персонал не должен быть местным и также не должен покидать карантин. Карантины должны охраняться Росгвардией. Первые две недели карантины должны быть индивидуальными.
Для остальных жителей России карантин может быть снят, или ослаблен.
Таблица прогноза сроков и максимального количества тяжелых больных.
| Дней до максимума эпидемии | Максимально тяжелых случаев за этот день | |
| Существующее положение | 39 | 108800 |
| Карантин | 65 | 65500 |
| Изоляция пожилых без общего карантина | 37 | 8700 |

Времени нет. Если оставить все как есть, к началу мая мы будем иметь сотни тысяч только тяжелых больных, нуждающихся в реанимации.Ежедневно будет поступать 100000 новых. Общий карантин растянет эти сроки вдвое и вдвое снизит приток больных.
Изоляция группы риска снизит количество тяжелых больных и смертей в 10 раз.
Хотелось бы донести эту информацию до властей.
Видео:Сколько решений имеет логическое уравнение: (A импликация В) ИЛИ (C импликация D). ЕГЭ(информатика)Скачать

Дифференциальные модели в экономике, биологии и медицине
В этом параграфе мы разберем несколько классических моделей, предложенных за последние 200 лет в различных областях науки: экономике, биологии и медицине. Общим при построении этих моделей является использование дифференциальных уравнений с разделяющимися переменными, которые несложно решить, прочитав §59 данного справочника.
п.1. Экономика. Равновесная цена в модели Вальраса
Начальные сведения о модели рыночного равновесия, кривых спроса и предложения – см. §18 справочника для 9 класса.
Рассмотрим поведение рыночной цены при небольшом отклонении от точки равновесия по методу, предложенному Леоном Вальрасом (1874 г.)
Пусть p — цена товара, D(p) — спрос на него, S(p) — предложение.
Пусть спрос и предложение на рынке уравновешены, равновесная цена равна (p_0).
Если спрос начнет немного превышать предложение, то цена начнет расти: $$ frac
=0, D(p_0)-S(p_0)=0 $$ Разложим каждую из функций с помощью дифференциала (см. §52 данного справочника) с точностью до линейного множителя: begin D(p)approx D(p_0)+D'(p_0)(p-p_0)\ S(p)approx S(p_0)+S'(p_0)(p-p_0) end Тогда разность спроса и предложения: begin D(p)-S(p)approx D(p_0)+D'(p_0)(p-p_0)-S(p_0)-S'(p_0)(p-p_0)=\ =underbrace_+left(D'(p_0)-S'(p_0)right)(p-p_0)=left(D'(p_0)-S'(p_0)right)(p-p_0) end Получаем уравнение с разделяющимися переменными: begin frac
Например:
Пусть (D(p)=9-frac
, S(p)=frac
)
(sqrt=y’x) — ДУ первого порядка первой степени
Тогда равновесная цена (9-frac
=frac
Rightarrow frac
=9Rightarrow p_0^2=36Rightarrow p_0=6)
Значения производных: begin D'(p)=0-frac=-frac p3, D'(p_0)=-2\ S'(p)=frac, S'(p_0)=1 end Изменение цены со временем в этом случае: $$ p(t)=6+(p(0)-6)e^=6+(p(0)-6)e^ $$ Построим графики для трех различных цен в начальный момент времени: $$ p(0)=left $$ (p(0)=5: p(t)=6-e^)
(p(0)=7: p(t)=6+e^)
(p(0)=9: p(t)=6+3e^)
Все три кривые постепенно сходятся к равновесной цене (p_0=6).
Устойчивое схождение к (p_0) будет наблюдаться только при условии: $$ D'(p_0)-S'(p_0)lt 0 $$ Т.е кривая спроса должна быть более крутой в своем спуске, чем кривая предложения на подъеме. Говорят, что эластичность спроса по цене в точке равновесия должна быть выше, чем эластичность предложения по цене.
Если степень при экспоненте будет положительной, (D'(p_0)-S'(p_0)gt 0) решение уходит на бесконечность. Говорят, что такое решение неустойчиво.
Если степень при экспоненте будет равна нулю, (D'(p_0)-S'(p_0)=0), цена не будет меняться и останется неравновесной.
п.2. Биология. Логистическое уравнение Ферхюльста для роста популяции
Пусть (P(t)) – численность популяции. Построим модель её изменения со временем.
Логично предположить, что прирост потомства в популяции пропорционален количеству особей, из чего получаем:
| Закон Мальтуса (1798 г.): $$ frac |
Решением этого уравнения будет (P(t)=P_0e^
| Закон Ферхюльста (1838 г.): $$ frac (K)- максимальный размер популяции в условиях ограниченных ресурсов. |
| Решение уравнения Ферхюльста (логистическая кривая): $$ P(t)=frac<KP_0e^ |
Например:
Пусть популяция растет со скоростью (r=0,1) тыс/год
Начальное количество особей (P_0=1) тыс
Максимальное количество, которое способна прокормить данная территория, (K=10) тыс
Модель показывает, что через 70 лет популяция займет всю нишу, и её рост фактически прекратится.
На начальном этапе преобладает r-стратегия: бурное размножение и короткая продолжительность жизни.
Исчерпание ресурсов заставляет переходить на K-стратегию: низкий темп размножения и долгую жизнь.
Экспериментально рост популяции по кривой Ферхюльста был подтвержден в лабораторных условиях для мух-дрозофил. В естественных условиях для животных – и тем более, в рамках социума для людей – закономерность нарушается.
п.3. Медицина. Модель развития эпидемии SIR
Традиционной моделью, описывающей процесс развития эпидемии, является модель SIR (Susceptible/Infected/Recovered), предложенная У. Кермаком и А. Маккендриком в 1927 г.
Вся популяция в модели делится на три группы:
- (S(t))— восприимчивые к инфекции, здоровые на момент времени (t);
- (I(t))— уже инфицированные;
- (R(t))— выздоровевшие, больше невосприимчивые к инфекции.
Популяция считается постоянной, т.е. (N=S(t)+I(t)+R(t)=const).
Рождаемость и смертность не учитывается.
Получаем следующую систему дифференциальных уравнений: $$ begin frac
Начальные условия в момент времени (t=0): $$ S(0)=S_0geq 0, I(0)=I_0geq 0, R(0)=R_0geq 0 $$ Переход из одной группы в другую можно изобразить линейной схемой:

| № | Переход одного человека из одной группы в другую | Скорость перехода |
| 1 | $$ (S;I)rightarrow (S-1; I+1) $$ | $$ betafrac $$ |
| 2 | $$ (I;R)rightarrow (I-1; R+1) $$ | $$ gamma I $$ |
Полученная система уравнений не является линейной и не имеет точного аналитического решения. Но её можно решить с использованием численных методов.
$$ begin frac=-betafrac\ frac=betafrac-gamma I(t)\ frac=gamma I(t) end $$ Считаем (triangle t=1) – следующий шаг итерации. Тогда: $$ begin S_-S_i=-betafrac\ I_-I_i=betafrac<S_I_i>-gamma I_i\ R_-R_i=gamma I_ end $$ Получаем следующий итеративный процесс: $$ begin S_=left(1-betafracright)S_i\ I_=left(1+betafrac<S_>-gamma right)I_i\ R_=gamma I_+R_i end $$ Знаний по информатике вам должно хватить, чтобы написать небольшой скрипт с циклом для этих уравнений и построить график.
Например:
Пусть общее количество населения N=10 тыс.чел.
В начальный момент инфицирован 1% населения: $$ S(0)=0,99N, I(0)=0,01N, R(0)=0 $$ Параметры: (beta=0,128; gamma=0,096) в расчете на день (эти параметры были рассчитаны по фактическим данным для лихорадки Эбола в Сьерра-Леоне).
Результат моделирования в MATLAB:
Красная кривая – это количество болеющих в данный момент. Как мы видим, к концу года она стремится к 0. Пик приходится на 70-80 дней с начала эпидемии и составляет 413 чел. или 4,13% населения.
Зеленая кривая – количество переболевших, к концу года выходит на асимптоту в 4700 чел. или 47,0% населения.
Синяя кривая – количество так и не заболевших, к концу года спускается на асимптоту в 5300 чел. или 53,0% населения.
Чем больше больных у вас будет в начале эпидемии и чем больше параметр (beta), тем выше будет пик (I_) для болеющих. Также, количество переболевших в конце эпидемии будет больше количества не заболевших.
Модель SIR – это начальный этап для исследований. На практике для моделирования эпидемий могут использоваться модели с десятками переходов и параметров, с постепенным усложнением по мере накопления данных.
Видео:Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.Скачать

Логистическое уравнение
Рассмотрим простое уравнение, применяемое для исследования роста численности популяции бактерий, животных и даже людей. Первую модель динамики роста населения Земли создал Мальтус. Он предположил, что скорость изменения численности населения 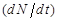
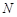
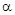
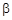
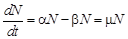
Здесь 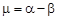
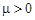
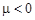
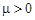
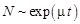
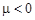
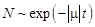
В то же время давно было замечено, что в популяциях животных экологическая система стабилизируется, т. е. численность животных через некоторое время перестает изменяться. Это обстоятельство толкнуло Ферхюльста в 1838 г. усовершенствовать модель Мальтуса и предложить логистическую модель:
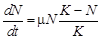
Здесь 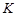
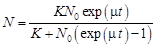
где 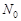
Это решение при малых временах ведет себя так же, как решение Мальтуса, но на больших временах 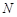
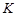
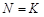
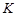
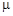
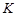
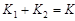
Логистические уравнения имеют достаточно простой вид, но приводят к большому разнообразию решений. Они описывают разнообразные явления не только в экологии. При помощи этих уравнений моделируются рост колонии дрожжевых грибов, динамика основных видов энергетических ресурсов, динамика распространения компьютеров на японском рынке, динамика построения метрополитена в разных городах мира и даже число людей, убитых «Красными бригадами» в Италии.
В заключение отметим, что логистическое уравнение является наиболее простым и активно используется в синергетике. Существует множество моделей, гораздо более сложных, которые предсказывают нетривиальное поведение открытых систем вдали от термодинамического равновесия.
Литература
Кудрявцев П.С. Курс истории физики. – М.: Просвещение, 1982. – 447 с.
Нараянамурти В. Кристаллические полупроводниковые гетероструктуры // Физика за рубежом. – М.: Мир, 1986. – С. 100–121.
Пригожин И., Кондепуди Д. Современная термодинамика. – М.: Мир, 2002. – 461 с.
Кикоин А.К., Кикоин И.К. Молекулярная физика. – М.: Наука, 1976. – 480 с.
Трубецков Д.И. Введение в синергетику. Хаос и структуры. – М., 2004. – 235 с.
🔍 Видео
Повторяем решение уравнений. Полезно всем! Вебинар | МатематикаСкачать

Логические выражения, таблицы истинности ,структурная логическая схемаСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Методы решения логических задач | Онлайн-школа Альфа. 5-6 классСкачать

Уравнение, которое меняет взгляд на мир [Veritasium]Скачать
![Уравнение, которое меняет взгляд на мир [Veritasium]](https://i.ytimg.com/vi/DH1cv0Rdf2w/0.jpg)
11 класс, 27 урок, Общие методы решения уравненийСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

ЗАКОНЫ АЛГЕБРЫ ЛОГИКИСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Математика это не ИсламСкачать

Матричный метод решения систем уравненийСкачать

Открытая лекция профессора В.С. Лукинского по логистике, TSI, 18.10.2013Скачать

Логистика. Логистическая система и операции.Скачать

Транспортная задача (закрытая, с циклом). Метод потенциалов - подробно и понятноСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Логистическая регрессияСкачать

Построение таблиц истинностиСкачать

Логистическая Регрессия для Дата СаентистаСкачать




