Логическое уравнение в дискретной математике

Правила математической логики определяют методы обоснования математических утверждений. Греческий философ Аристотель был пионером логических рассуждений. Логические рассуждения обеспечивают теоретическую основу для многих областей математики и, следовательно, информатики. Он имеет множество практических приложений в области компьютерных наук, таких как проектирование вычислительных машин, искусственный интеллект, определение структур данных для языков программирования и т. Д.

Логика высказываний связана с утверждениями, которым могут быть присвоены значения истинности «истина» и «ложь». Цель состоит в том, чтобы проанализировать эти утверждения по отдельности или в совокупности.

Предлогическая логика — определение

Предложение — это совокупность декларативных утверждений, которые имеют либо значение истины «истина», либо значение истины «ложь». Пропозициональное предложение состоит из пропозициональных переменных и связок. Мы обозначаем пропозициональные переменные заглавными буквами (A, B и т. Д.). Связки соединяют пропозициональные переменные.

Некоторые примеры предложений приведены ниже —

• «Человек — смертный», он возвращает истинное значение «ИСТИНА»
• «12 + 9 = 3 — 2», возвращает значение истинности «ЛОЖЬ»

Следующее не является предложением —

«А меньше 2». Это потому, что если мы не дадим конкретное значение A, мы не сможем сказать, является ли утверждение истинным или ложным.

«А меньше 2». Это потому, что если мы не дадим конкретное значение A, мы не сможем сказать, является ли утверждение истинным или ложным.

Связки

В логике высказываний мы обычно используем пять связок, которые:

Отрицание / НЕ ( l n o t )

Импликация / если-тогда ( r i g h t a r r o w )

Если и только если ( L e f t r i g h t a r r o w ).

Отрицание / НЕ ( l n o t )

Импликация / если-тогда ( r i g h t a r r o w )

Если и только если ( L e f t r i g h t a r r o w ).

OR ( l o r ) — Операция OR двух предложений A и B (записанная как A l o r B ) выполняется, если хотя бы любая из пропозициональных переменных A или B истинна.

Таблица истинности выглядит следующим образом —

В	A ∨ B
Правда	Правда	Правда
Правда	Ложь	Правда
Ложь	Правда	Правда
Ложь	Ложь	Ложь

AND ( l a n d ) — Операция AND двух предложений A и B (записанная как A l a n d B ) верна, если обе пропозициональные переменные A и B верны.

Таблица истинности выглядит следующим образом —

В	A ∧ B
Правда	Правда	Правда
Правда	Ложь	Ложь
Ложь	Правда	Ложь
Ложь	Ложь	Ложь

Отрицание ( l n o t ) — отрицание предложения A (записанного как l n o t A ) ложно, когда A истинно, и истинно, когда A ложно.

Таблица истинности выглядит следующим образом —

¬ A
Правда	Ложь
Ложь	Правда

Импликация / если-тогда ( r i g h t a r r o w ) — импликация A r i g h t a r r o w B — это предложение «если A, то B». Это ложно, если A верно, а B ложно. Остальные случаи верны.

Таблица истинности выглядит следующим образом —

В	A → B
Правда	Правда	Правда
Правда	Ложь	Ложь
Ложь	Правда	Правда
Ложь	Ложь	Правда

Если и только если ( L e f t r i g h t a r r o w ) — A L e f t r i g h t a r r o w B — это двухусловное логическое связующее, которое истинно, когда p и q одинаковы, т.е. оба являются ложными или оба истинны.

Таблица истинности выглядит следующим образом —

В	A ⇔ B
Правда	Правда	Правда
Правда	Ложь	Ложь
Ложь	Правда	Ложь
Ложь	Ложь	Правда

Тавтологии

Тавтология — это формула, которая всегда верна для каждого значения ее пропозициональных переменных.

Пример — Доказать, что l b r a c k ( A r i g h t a r r o w B ) l a n d A r b r a c k r i g h t a r r o w B — тавтология

Таблица истинности выглядит следующим образом —

В	A → B	(A → B) ∧ A	[(A → B) ∧ A] → B
Правда	Правда	Правда	Правда	Правда
Правда	Ложь	Ложь	Ложь	Правда
Ложь	Правда	Правда	Ложь	Правда
Ложь	Ложь	Правда	Ложь	Правда

Как мы видим, каждое значение l b r a c k ( A r i g h t a r r o w B ) l a n d A r b r a c k r i g h t a r r o w B равно «True», это тавтология.

Противоречия

Противоречие — это формула, которая всегда ложна для каждого значения ее пропозициональных переменных.

Пример — Докажите, что ( A l o r B ) l a n d l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k является противоречием

Таблица истинности выглядит следующим образом —

В	A ∨ B	¬ A	¬ B	(¬ A) ∧ (¬ B)	(A ∨ B) ∧ [(¬ A) ∧ (¬ B)]
Правда	Правда	Правда	Ложь	Ложь	Ложь	Ложь
Правда	Ложь	Правда	Ложь	Правда	Ложь	Ложь
Ложь	Правда	Правда	Правда	Ложь	Ложь	Ложь
Ложь	Ложь	Ложь	Правда	Правда	Правда	Ложь

Как мы видим, каждое значение ( A l o r B ) l a n d l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k равно «False», это противоречие.

непредвиденные обстоятельства

Непредвиденные обстоятельства — это формула, которая имеет как истинные, так и ложные значения для каждого значения своих пропозициональных переменных.

Пример — Доказать непредвиденную случайность в ( A l o r B ) l a n d ( l n o t A )

Таблица истинности выглядит следующим образом —

В	A ∨ B	¬ A	(A ∨ B) ∧ (¬ A)
Правда	Правда	Правда	Ложь	Ложь
Правда	Ложь	Правда	Ложь	Ложь
Ложь	Правда	Правда	Правда	Правда
Ложь	Ложь	Ложь	Правда	Ложь

Как мы видим, каждое значение ( A l o r B ) l a n d ( l n o t A ) имеет «True» и «False», это непредвиденное обстоятельство.

Пропозициональные эквивалентности

Два утверждения X и Y логически эквивалентны, если выполняется любое из следующих двух условий:

Таблицы истинности каждого утверждения имеют одинаковые значения истинности.

Двухусловное утверждение X L e f t r i g h t a r r o w Y является тавтологией.

Таблицы истинности каждого утверждения имеют одинаковые значения истинности.

Двухусловное утверждение X L e f t r i g h t a r r o w Y является тавтологией.

Пример — Докажите, что l n o t ( A l o r B ) и l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k эквивалентны

Тестирование по 1- му методу (таблица соответствия)

В	A ∨ B	¬ (A ∨ B)	¬ A	¬ B	[(¬ A) ∧ (¬ B)]
Правда	Правда	Правда	Ложь	Ложь	Ложь	Ложь
Правда	Ложь	Правда	Ложь	Ложь	Правда	Ложь
Ложь	Правда	Правда	Ложь	Правда	Ложь	Ложь
Ложь	Ложь	Ложь	Правда	Правда	Правда	Правда

Здесь мы видим, что значения истинности l n o t ( A l o r B ) и l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k совпадают, поэтому утверждения эквивалентны.

Тестирование по 2- му методу (би-условность)

В	¬ (A ∨ B)	[(¬ A) ∧ (¬ B)]	[¬ (A ∨ B)] ⇔ [(¬ A) ∧ (¬ B)]
Правда	Правда	Ложь	Ложь	Правда
Правда	Ложь	Ложь	Ложь	Правда
Ложь	Правда	Ложь	Ложь	Правда
Ложь	Ложь	Правда	Правда	Правда

Поскольку l b r a c k l n o t ( A l o r B ) r b r a c k L e f t r i g h t a r r o w l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k является тавтологией, утверждения эквивалентны.

Обратное, Обратное и Противоположительное

Импликация / if-then ( r i g h t a r r o w ) также называется условным оператором. Он состоит из двух частей —

Как упоминалось ранее, он обозначается как p r i g h t a r r o w q .

Пример условного высказывания — «Если вы делаете свою домашнюю работу, вы не будете наказаны». Здесь «вы делаете свою домашнюю работу» — это гипотеза, p, а «вы не будете наказаны» — это заключение, q.

Обратное . Обратным условным утверждением является отрицание как гипотезы, так и заключения. Если утверждение «Если р, то q», обратное будет «Если не р, то не q». Таким образом, обратное значение p r i g h t a r r o w q равно l n o t p r i g h t a r r o w l n o t q .

Пример . Обратное выражение «Если вы делаете домашнее задание, вы не будете наказаны» — «Если вы не будете выполнять домашнее задание, вы будете наказаны».

Обратное — обратное условное утверждение вычисляется путем обмена гипотезы и заключения. Если утверждение «Если р, то д», обратное будет «Если д, то р». Обратным к p r i g h t a r r o w q является q r i g h t a r r o w p .

Пример . Обратное выражение «Если вы делаете домашнее задание, вы не будете наказаны» — «Если вы не будете наказаны, вы делаете домашнее задание».

Противоположный — Противоположный условного рассчитывается путем обмена гипотезы и заключения обратного утверждения. Если утверждение «Если p, то q», то противоположным будет «Если не q, то не p». Противоположным для p r i g h t a r r o w q является l n o t q r i g h t a r r o w l n o t p .

Пример — Противоположный вариант «Если вы делаете домашнее задание, вы не будете наказаны» — «Если вы наказаны, вы не сделали домашнее задание».

Принцип двойственности

Принцип двойственности гласит, что для любого истинного утверждения двойственное утверждение, полученное путем взаимного объединения союзов в пересечения (и наоборот) и взаимного изменения универсального множества в нулевое множество (и наоборот), также верно. Если дуальным каким-либо утверждением является само утверждение, оно называется самодвойственным утверждением.

Пример — двойственное значение ( A c a p B ) c u p C равно ( A c u p B ) c a p C

Нормальные Формы

Мы можем преобразовать любое предложение в две нормальные формы —

• Конъюнктивная нормальная форма
• Дизъюнктивная нормальная форма

Конъюнктивная нормальная форма

Составной оператор находится в конъюнктивной нормальной форме, если он получен путем операции И среди переменных (включая отрицание переменных), связанных с ИЛИ. С точки зрения операций над множествами, это составное утверждение, полученное Intersection среди переменных, связанных с Unions.

( A l o r B ) з е м л я ( A l o r C ) з е м л я ( B l o r C l o r D )

( P c u p Q ) c a p ( Q c u p R )

( A l o r B ) з е м л я ( A l o r C ) з е м л я ( B l o r C l o r D )

( P c u p Q ) c a p ( Q c u p R )

Дизъюнктивная нормальная форма

Составной оператор находится в конъюнктивной нормальной форме, если он получен путем операции ИЛИ среди переменных (включая отрицание переменных), связанных с AND. С точки зрения операций над множествами, это составное утверждение, полученное объединением среди переменных, связанных с пересечениями.

( A l a n d B ) l o r ( A l a n d C ) l o r ( B l a n d C l a n d D )

Алгебра логики

Содержание:

Алгебра логики является частью, разделом бурно развивающейся сегодня науки — дискретной математики. Дискретная математика занимается изучением свойств структур конечного характера, которые возникают как внутри математики, так и в ее приложениях.

• Заметим, что классическая математика, в основном, занимается изучением свойств объектов непрерывного характера, хотя само деление математики на классическую и дискретную в значительной мере условно, поскольку между ними происходит активная циркуляция идей и методов, часто возникает необходимость исследовать модели, обладающие как дискретными, так и непрерывными свойствами.

К числу структур, изучаемых дискретной математикой, могут быть отнесены конечные группы, конечные графы, математические модели преобразователей информации типа конечных автоматов или машин Тьюринга и др. Математический аппарат алгебры логики широко используется в информатике, в частности, в таких ее разделах, как проектирование ЭВМ, теория автоматов, теория алгоритмов, теория информации, целочисленное программирование и т. д. Алгебра логики.

Понятие высказывания Алгебра логики изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству (например,). Иногда вместо термина «алгебра логики» употребляют термин «двузначная логика». Отцом алгебры логики по праву считается английский математик XIX столетия Джордж Буль.

Именно он построил один из разделов формальной логики в виде некоторой «алгебры», аналогичной алгебре чисел, но не сводящейся к ней. Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами.

Существуют алгебры натуральных чисел, многочленов, векторов, матриц, множеств и т. д. Дж. Буль (1815-1864) Долгое время алгебра логики была известна достаточно узкому классу специалистов.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Прошло почти 100 лет со времени создания алгебры логики Дж. Булем, прежде чем в 1938 году выдающийся американский математик и инженер Клод Шеннон (1916-2001) показал, что алгебра логики применима для описания самых разнообразных процессов, в том числе функционирования ре-лейно-контактных и электронно-ламповых схем. Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики).

• С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно. Примерами высказываний на естественном языке являются предложения «Сегодня светит солнце» или «Трава растет». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в нашем примере погоды и окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь».

Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна » устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным. Что же является высказыванием в формальной логике?

Определение 1. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).

Возможно вам будут полезны данные страницы:

Это словесное определение, не являющееся математически точным, только на первый взгляд кажется удовлетворительным. Оно отсылает проблему определения высказывания к проблеме определения истинности или ложности данного языкового образования. Если рассматривать в качестве высказываний любые утвердительные предложения, то это быстро приводит к парадоксам и противоречиям. Например, предложению «Это предложение является ложным» невозможно приписать никакого значения истинности без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит его смыслу. Если же принять, что предложение ложно, то отсюда следует, что предложение на самом деле истинно.

• Как видно, этому предложению осмысленно нельзя приписать какое-либо значение истинности, следовательно, оно не является высказыванием. Причина этого парадокса лежит в структуре построения указанного предложения: оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя и, следовательно, устранены возникающие отсюда парадоксы.

Определение 2. Высказывание называется простым (элементарным)I, если никакая его часть не является высказыванием.

Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывание, соединив их знаком равенства или неравенства. Сами числовые выражения высказываниями не являются. Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «» становится высказыванием при замене переменной каким-либо конкретным значением. Предложения типа «» называют предикатами. Алгебра логики отвлекается от смысловой содержательности высказываний.

Мы можем договориться, что абсурдное по смыслу высказывание «Крокодилы летают» является истинным, и с этим значением высказывания будем работать. Вопрос о том, летают крокодилы или нет, может волновать зоологов, но никак не математиков: им этот потрясающий факт безразличен. Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания. В информатике для точного определения понятия высказывания строятся ограниченные системы форм высказываний (формальный язык), которые используются при описании алгоритмических языков, в информационных системах, для строгого формального описания алгоритмов и т. д.

Логические операции. Таблицы истинности

Употребляемые в обычной речи связки «и», «или», «не», «если . то . », «тогда и только тогда, когда . » и т. п. позволяют из уже заданных высказываний строить новые сложные высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как логических операций над высказываниями. Для обозначения истинности, как правило, используются символы «И» и «1», а для обозначения ложности — символы «Л» и «0».

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний. В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:

Введем перечисленные логические операции формальным образом. Высказывание, составленное из двух высказываний путем объединения их связкой «и», называется конъюнкцией или логическим умножением. Высказывая конъюнкцию, мы утверждаем, что выполняются оба события, о которых идет речь в составляющих высказываниях.

Например, сообщая: , мы выражаем в одном высказывании свое убеждение в том, что произошли оба этих события.

Определение 3. Конъюнкция — логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Логическая операция конъюнкция определяется следующей таблицей, которую называют таблицей истинности:

Рассмотрим два высказывания = <Завтра будет мороз) и . Очевидно, новое высказывание = истинно только в том случае, когда одновременно истинны высказывания а именно, когда истинно, что завтра будет и мороз, и снег.

Высказывание будет ложно во всех остальных случаях: будет идти снег, но будет оттепель (т. е. не будет мороза); мороз будет, а снег не будет идти; не будет мороза, и снег не будет идти. В русском языке конъюнкции соответствует не только союз «и», но и другие речевые обороты, например связки «а» или «но».

Высказывание, состоящее из двух высказываний, объединенных связкой «или», называется дизъюнкцией или логическим сложением, нестрогой дизъюнкцией.

В высказываниях, содержащих связку «или», указывается на существование двух возможных событий, из которых хотя бы одно должно быть осуществлено. Например, сообщая: <Петя читает книгу или пьет чай), мы имеем в виду, что хотя бы что-либо одно Петя делает. При этом Петя может одновременно читать книгу и пить чай. И в этом случае дизъюнкция будет истинна.

Определение 4. Дизъюнкция — логическая операция, которая каждым двум элементарным высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Логическая операция дизъюнкция определяется следующей таблицей истинности:

Дизъюнкция истинна, когда хотя бы одно из двух образующих ее высказываний истинно. Рассмотрим два высказывания = <Колумб был в Индии) и = . Очевидно, новое высказывание = истинно как в случае, если Колумб был в Индии, но не был в Египте, так и в случае, если он не был в Индии, но был в Египте, а также в случае, если он был и в Индии, и в Египте. Но это высказывание будет ложно, если Колумб не был ни в Индии, ни в Египте.

Союз «или» может применяться в речи и в другом, «исключающем» смысле. Тогда он соответствует другому высказыванию — разделительной, или строгой дизъюнкции. 3.2.3. Высказывание, образованное из двух высказываний, объединенных связкой «либо» (точнее: «либо только . либо только . »), называется разделительной (строгой) дизъюнкцией, исключающим ИЛИ, сложением по модулю 2.

В отличие от обычной дизъюнкции (связка «или»), в высказывании, являющемся разделительной дизъюнкцией, мы утверждаем, что произойдет только одно событие из двух. Например, сообщая: , мы утверждаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б.

Определение 5. Строгая, или разделительная дизъюнкция — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда ровно одно из двух высказываний является истинным.

Логическая операция разделительная дизъюнкция определяется следующей таблицей истинности:

Рассмотрим два высказывания — <Кошка охотится за мышами) и — <Кошка спит на диване). Очевидно, что новое высказывание истинно только в двух случаях: когда кошка охотится за мышами или когда кошка мирно спит. Это высказывание будет ложно, если кошка не делает ни того, ни другого, т. е. когда оба события не происходят. Но это высказывание будет ложным и тогда, когда предполагается, что оба события будут происходить одновременно.

Определение 6. Импликация — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда условие (посылка) — истинно, а следствие (заключение) — ложно.

Логическая операция импликация задается следующей таблицей истинности:

Мы видим, что импликация заведомо истинна, если условие ложно. Другими словами, из неверного условия может следовать все, что угодно. Например, высказывание <Если то крокодилы летают) является истинным. Подавляющее число зависимостей между событиями можно описать с помощью импликации.

Примеры с решением

Пример 1.

Следующие две импликации являются ложными, так как в них посылки истинны, а заключения ложны:

Может показаться странным, что высказывание «Если А, то В>> всегда истинно, если посылка (высказывание Л) ложна. Но для математика это вполне естественно. В самом деле, исходя из ложной посылки, можно путем верных рассуждений получить как истинное, так и ложное утверждение. Допустим, что 1 = 2, тогда и 2 = 1. Складывая эти равенства, получим 3 = 3, т. е. из ложной посылки путем тождественных преобразований мы получили истинное высказывание.

Большинство математических теорем являются импликациями. Однако те импликации, в которых посылки (условия) и заключения (следствия) являются предложениями без взаимной (по существу) связи, не могут играть в науке важной роли. Они являются бесплодными предложениями, так как не ведут к выводам более глубокого содержания.

Логические формулы. Законы алгебры логики

Математики под словом «алгебра» подразумевают науку, которая изучает некие объекты и операции над ними. Например, школьная алгебра (алгебра действительных чисел) изучает действительные числа и операции над ними. Предметом же нашего изучения являются высказывания, операции над ними, а также логические функции. В предыдущих параграфах для обозначения высказываний мы использовали буквы. Как и в алгебре действительных чисел, введем следующие определения.

Определение 9. Логической переменной называется переменная, значением которой может быть любое высказывание.

Логические переменные (далее «переменные») обозначаются латинскими буквами, иногда снабженными индексами, как обычные алгебраические переменные: и т. п.

Понятие логической формулы является формализацией понятия сложного высказывания. Введем его индуктивно. Определение 10. Логической формулой является: 1) любая логическая переменная, а также каждая из двух логических констант — 0 (ложь) и 1 (истина); 2) если А и В — формулы, то В и А*В — тоже формулы, где знак «*» означает любую из логических бинарных операций. Формулой является, например, следующее выражение: Каждой формуле при заданных значениях входящих в нее переменных приписывается одно из двух значений — 0 или 1.

Определение 11. Формулы А и В, зависящие от одного и того же набора переменных называют равносильными или эквивалентными, если на любом наборе значений переменных они имеют одинаковые значения.

Для обозначения равносильности формул используется знак равенства, например А В. В дальнейшем будет показано, что любую формулу можно преобразовать к равносильной ей, в которой используются только аксиоматически введенные операции и отрицание. Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, которые по аналогии с алгеброй вещественных чисел будем называть законами:

1) законы коммутативности

2) законы ассоциативности

3) законы поглощения (нуля и единицы)

4) законы дистрибутивности

5) закон противоречия

6) закон исключенного третьего

7) законы идемпотентности

8) закон двойного отрицания

9) законы де Моргана

10) законы поглощения

Любой из этих законов может быть легко доказан с помощью таблиц истинности.

Пример 2.

Докажем первый закон де Моргана с использованием таблиц истинности. Построим таблицу истинности для левой и правой частей закона.

Так как результирующие столбцы совпали, то формулы, стоящие в левой и правой частях закона, равносильны. Любой из законов алгебры логики может быть доказан путем логических рассуждений.

Пример 3.

Докажем первый закон поглощения путем логических рассуждений. Для этого достаточно показать, что если правая часть истинна, то и левая часть истинна, и что если левая часть истинна, то и правая часть истинна.

Пусть истинна правая часть, т. е. тогда в левой части дизъюнкция истинна по определению дизъюнкции.

Пусть истинна левая часть. Тогда по определению дизъюнкции истинна или формула или формула или обе эти формулы одновременно.

Если ложна, тогда ложна, следовательно, х может быть только истинной. Еще одним способом вывода законов являются тождественные преобразования. Пример 9. Первый закон поглощения можно вывести при помощи законов поглощения единицы и дистрибутивности:

Методы решения логических задач Исходными данными в логических задачах являются высказывания. Эти высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов достаточно трудно.

Многие логические задачи связаны с рассмотрением нескольких конечных множеств и связей между их элементами. Для решения таких задач зачастую прибегают к помощи таблиц или графов, при этом успешность решения во многом зависит от удачно выбранной структуры таблицы или графа. Аппарат же алгебры логики позволяет построить формальный универсальный способ решения логических задач.

Рассмотрим, как можно использовать данный способ для решения задач.

Пример 4.

Задача «Уроки логики». На вопрос, кто из трех учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?

Решение. Обозначим через высказывания, состоящие в том, что соответственно первый, второй, третий учащийся изучали логику. Из условия задачи следует истинность высказывания Воспользуемся соотношением и упростим исходное высказывание:

Высказывание ложно, а следовательно, ложно и высказывание . Поэтому должно быть истинным высказывание а.это означает, что логику изучал третий учащийся, а первый и второй не изучали. Для решения следующей задачи составим логическое выражение, удовлетворяющее всем условиям, затем заполним для него таблицу истинности. Анализ полученной таблицы истинности позволит получить требуемый результат.

Пример 5.

Задача «Кто виноват?» По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено: 1) если Иванов не виновен или Петров виновен, то Сидоров виновен; 2) если Иванов не виновен, то Сидоров не виновен. Виновен ли Иванов? Решение. Рассмотрим простые высказывания: А = , В = , С = . Запишем на языке алгебры логики факты, установленные следствием: Обозначим — единое логическое выражение для всех требований задачи. Оно истинно. Составим для него таблицу истинности:

Решить данную задачу — значит указать, при каких значениях А полученное сложное высказывание F истинно. Для этого необходимо проанализировать все строки таблицы истинности, где И если хотя бы в одном из таких случаев (Иванов не виновен), то у следствия недостаточно фактов для того, чтобы обвинить Иванова в преступлении. Анализ таблицы показывает, что высказывание истинно только в тех случаях, когда истинно, т. е. Иванов в ограблении виновен. Иногда, для того чтобы решить задачу, нет необходимости составлять единое логическое выражение, удовлетворяющее всем условиям задачи, достаточно построить таблицу истинности, отражающую каждое условие задачи, и проанализировать ее.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

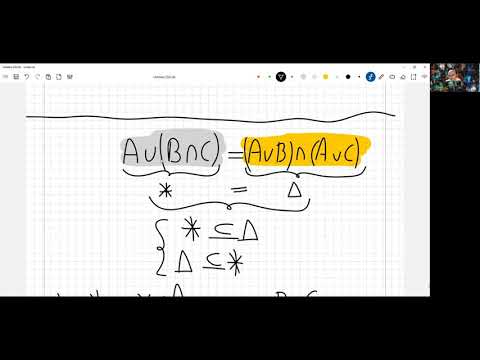
Учебное пособие: Дискретная математика

Российский химико-технологический университет

им. Д.И. Менделеева

T.П. Тюрина, В.И. Емельянов

Часть 3. Элементы алгебры логики. 3

3.1 Введение в алгебру логики. 3

3.2 Основные функции алгебры логики. 5

3.3 Формулы алгебры логики. 9

Контрольные вопросы. 12

3.4 Законы алгебры логики и следствия из них. 12

Контрольные вопросы. 16

3.5 Логические функции многих переменных. 16

3.6 Построение формул алгебры логики по заданной таблице истинности 18

Контрольные вопросы и упражнения. 26

3.7 Некоторые замкнутые классы (классы Поста). Понятие базиса. 26

Контрольные вопросы и упражнения. 34

3.8 Методы минимизации логических функций. 34

Контрольные вопросы. 39

3.9 Неполностью определенные логические функции. 40

3.10 Формы представления булевых функций. 41

3.10.1 Семантические деревья. 42

3.10.2 Бинарные диаграммы решений (БДР). 45

3.11 Построение логических схем. 45

Контрольные вопросы. 45

3.12 Логические конечные автоматы. 46

3.12.1 Процессы. 50

3.12.2 Конечные автоматы. 52

Контрольные вопросы. 55

БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 60

Часть 3. Элементы алгебры логики

3.1 Введение в алгебру логики

Алгебру логики иначе еще называют алгеброй высказываний, логикой высказываний. Алгебра логики начала формироваться в 19 веке в трудах английского математика Дж. Буля.

Прежде всего, благодаря труду английского логика Джорджа Буля «Математический анализ логики», был достигнут подлинный прогресс науки, называемый математической логикой. Он перенёс на логику законы и правила математических действий, ввёл логические операции, предложил способ записи высказываний в символической форме.

В трудах Джорджа Буля и О. де Моргана математическая логика представлена как своеобразная алгебра – алгебра логики (алгебра высказываний).

Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.

Джордж Буль (1815–1864) родился в Линкольне (Англия). Сын сапожного мастера. Окончил только начальную школу и дальнейшие знания приобретал самоучкой. С 1849 г. Буль – профессор математики в Куинс – колледже в Корке (Ирландия), где преподавал до конца жизни. Буля почти в равной степени интересовали логика, математический анализ, теория вероятностей, этика Б. Спинозы, философские работы Аристотеля и Цицерона. Он считается несомненным создателем современной символической (математической) логики.

Огастес де Морган (1806–1871) родился в Индии в семье полковника английских войск. Получил образование в Кембриджском университете. Был профессором математики Лондонского университета. Математику и логику де Морган назвал азами точного знания и выражал сожаление, что математики не более заботятся о логике, чем логики о математике. Сам он стремился сблизить обе науки, и его главной заслугой явилось построение логики по образу и подобию математических наук. Независимо от Дж. Буля он открыл основные идеи алгебры логики.

«Логика Буля» основывается на отношении эквивалентности, при котором правая часть равенства всегда содержит ровно столько же «истин», сколько и левая.

Высказывание – это имеющее смысл языковое выражение (повествовательное предложение), относительно которого в данной ситуации можно утверждать, что оно либо истинно, либо ложно, т. е. каждому высказыванию можно приписать истинное значение И (истина) или Л (ложь), но не то и другое одновременно.

1. НГТУ – крупнейший «вуз Новосибирска».

3. Р= «Чтобы подключиться к Интернету с домашнего компьютера, необходим модем и соответствующее ПО».

4. Крокодилы летают очень низко.

«А ты любишь информатику?» – это предложение не является высказыванием.

Уравнение 2+х=4 не является высказыванием. Однако, всякий раз, придавая переменной х определенное числовое значение, будем получать высказывание. Используя частицу «не», а также союзы «и», «или», связки «если …., то…», «тогда и только тогда, когда…» и т. п., можно из одних высказываний строить другие высказывания.

Изучением высказываний занимается Булева алгебра, в которой предполагается, что уже имеется некоторый запас высказываний, для каждого из которых известно истинно оно или ложно. Такие высказывания называют элементарными высказываниями. Из элементарных высказываний могут быть построены сложные с помощью операций алгебры логики.

Знаки логических операций называют логическими связками (или просто связками). Логические связки могут быть одноместные (унарные), двухместные (бинарные), трехместные (тернарные) и т. д.

В алгебре логики логические операции чаще всего описываются при помощи таблиц истинности, содержащих все наборы значений переменных и значения функции этих наборов. Алгебра логики не занимается обоснованием того, почему тому или иному элементарному высказыванию приписано значение истины или лжи. Этот вопрос решается за пределами алгебры логики.

Например: сумма углов в треугольнике – 180 градусов. Алгебра логики отвлекается и от смысловой содержательности высказывания. Она интересуется только одним свойством сложных высказываний: быть истинным (True – 1) или ложным (False – 0).

3.2 Основные функции алгебры логики

Основной задачей теории булевых функций является разработка систематического метода построения сложных функций из более простых. Этот метод основан на изучении свойств булевых функций.

Основными символами алгебры высказываний являются:

а) пропозиционные переменные Р1, Р2, Р3 , …;

б) одноместная связка – (ù) и двуместные связки Ù (и), Ú (или), ®, Þ, Û;

Переменная, значениями которой являются высказывания, называется пропозиционной переменной.

Пусть А, В- некоторые элементарные высказывания.

Определим новое высказывание Ā (т. е. не А ), будем называть его отрицанием (инверсия: , Ā ), представим таблицы значений функции отрицания:

Рассмотрим наборы истинных значений элементарных функций на наборах аргументов:

Название: Дискретная математика Раздел: Рефераты по математике Тип: учебное пособие Добавлен 02:09:02 30 апреля 2009 Похожие работы Просмотров: 5631 Комментариев: 20 Оценило: 4 человек Средний балл: 4.3 Оценка: неизвестно Скачать

№	Обозначение операции	Другие обозначения	Набор истинных значений	Название логической опции и связки	Как читается	Арифметическая модель
12	АÚВ	Дизъюнкция, логическое сложение, «или»	А или В	A+B-A×B
23	АÙВ	Конъюнкция, логическое умножение «и»	А и В	A×B
34	А®В	Импликация, логическое следование	1‑A+ A×B
45	А	Эквиваленция, эквивалентность	А тогда и только тогда, когда В; А эквивалентно В	1 – (A-B) 2
56	АÅВ	Сумма по модулю 2, сумма Жегалкина	А плюс В; Либо А, либо В
67	А½В	Штрих Шеффера, антиконъюнкция	Неверно, что А и В; А штрих Шеффера В
78	А¯В	Стрелка Пирса, антидизъюнкция, функция Вебба, функция Даггера	Ни А, ни В; А стрелка Пирса В

Несмотря на то, что булевых функций от любого заданного числа m двоичных переменных конечное число, их слишком много, чтобы иметь запас преобразователей для любых встретившихся отображений. Рассмотрим сначала все возможные функции от одной двоичной переменной. Их четыре, две из них – константы (0 и 1), одна – тождественная функция и только одна – функция отрицания (функция НЕ) – является нетривиальной.

p	p
0	1
1	0

Очевидно, что число различных булевых функций от m переменных равно 2 в степени . При m = 2 это число 16, то есть всего функций от двух переменных 16, однако наиболее практически применимых из них меньше.

Суперпозиция двоичных функций может быть записана как формула, которую называют логической формулой.

Логическая формула задает функцию от трех переменных как суперпозицию функций одной и двух переменных.

Для уменьшения числа скобок вводятся приоритеты операций. Наиболее приоритетна функция отрицания. Затем идет конъюнкция, после нее – дизъюнкция. Все другие функции имеют равный приоритет, меньший, чем у дизъюнкции. Очевидно, что скобками можно установить желаемый порядок операций. Вышеприведенная формула может быть эквивалентно записана так: . Отметим, что используют и другое распределение приоритетов, в частности, полагая импликацию менее приоритетной, чем все другие функции.

Логическая формула дает возможность построить соответствующий функциональный преобразователь, если мы имеем «элементарные» или «базисные» преобразователи. Для реализации преобразователя f примера выше необходимо иметь элементы, реализующие отрицание, дизъюнкцию, конъюнкцию и сложение по модулю два (см. рис. 1).

На этом рисунке представлен пример синтаксической структуры формулы – графическое представление формулы.

Рис. 1. Синтаксическая структура формулы

Очевидным образом по формуле можно построить табличное представление функции f .

p	q	r
0	0	0	1	1	0	0	0	1
0	0	1	1	1	0	1	0	1
0	1	0	1	1	0	0	0	1
0	1	1	1	1	1	1	1	0
1	0	0	0	0	0	1	0	0
1	0	1	0	0	0	1	0	0
1	1	0	0	1	0	1	0	1
1	1	1	0	1	1	1	1	0

Суперпозицией нескольких простых булевых функций можно построить более сложную функцию, в частности, булеву функцию от большего числа переменных. Поставим вопрос: можно ли суперпозицией фиксированного набора функций представить любую булеву функцию от любого числа переменных? Удивительно, но ответ на этот вопрос положителен.

Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности.

М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики.

Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник прагматизма.

3.3 Формулы алгебры логики

Из логических переменных можно составлять различные конструкции, которые образуют формулы алгебры логики.

Пусть – некоторое множество логических переменных. По индукции определим понятие формулы алгебры логики:

1) любая логическая переменная является формулой (атомарной);

2) если и – формулы, то выражения и другие, представленные в табл. 1, являются формулами;

3) никаких других формул, кроме построенных в пунктах 1 и 2, нет.

Если формула построена из логических переменных, лежащих в множестве <x ₁ , x ₂ ,…, x_n >, то будем писать <x ₁ , x ₂ ,…, x_n >.

Таблицы истинности также называются интерпретациями логических операций и составляют семантику формул (т. е. придание смысла формулам) в отличие от синтаксиса формул (т. е. формальных законов их построения, данных в определении формулы).

На множестве вводится транзитивное отношение N ).

Равносильными называются два высказывания, у которых таблицы истинности совпадают.

Пример. Составим таблицу истинности функции f=(A B )

():

Полученное высказывание истинно всегда. Такие высказывания называют тождественно истинными и обозначаются J . По аналогии существуют и тождественно ложные высказывания L . Метод заполнения таблицы истинности принят для не очень сложных высказываний. Если выражение содержит N опций, то таблица становится громоздкой. Для этого используются законы алгебры логики. Таблицу истинности можно составить с использованием программы. В большинстве языков высокого уровня имеются логические операции NOT , AND , OR , XOR , реализующие операции соответственно.

Контрольные вопросы

1. Дайте определение высказывания.

2. Перечислите основные символы алгебры высказываний.

3. Перечислите основные функции алгебры логики.

4. Что является основной задачей алгебры логики?

5. Что такое таблицы истинности логических функций?

6. Составьте таблицу истинности функций дизъюнкции и конъюнкции.

7. Составьте таблицу истинности функций импликации и эквивалентности.

8. Составьте таблицу истинности функций отрицания и сложения по модулю 2.

9. Составьте таблицу истинности функций Штрих Шеффера и Стрелка Пирса.

10. Формулы алгебры логики. Приоритет логических операций. Какие отношения имеют место на множестве логических операций?

11. Что такое синтаксическая структура формулы?

12. На какие классы делятся формулы алгебры логики?

3.4 Законы алгебры логики и следствия из них

При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре логики производится на основе эквивалентных преобразований, опирающихся на основные логические законы. Законы алгебры логики – это тавтологии (или теоремы).

1. Закон тождества:

2. Закон непротиворечия:

3. Закон исключения третьего:

4. Закон двойного отрицания:

5. Законы истины и лжи (свойства констант):

6. Законы идемпотентности:

7. Коммутативные законы:

8. Ассоциативные законы:

– дизъюнкции

– конъюнкции

9. Дистрибутивные законы:

– 1‑ый дистрибутивный закон

– 2‑ой дистрибутивный закон

10. Законы поглощения:

11. Законы де Моргана:

12. Закон импликации:

13. Закон эквивалентности:

14. Свойства сложения «по модулю два»:

Справедливость этих законов можно доказать с помощью таблиц истинности сложных логических связей описываемых законов.

Следствия из законов алгебры логики (часто используются при упрощении логических выражений).

1. Правило поглощения. Данное правило является следствием из дистрибутивного закона. Оно может быть записано в следующем виде:

.

2. Правило свертки. Правило является следствием из второго дистрибутивного закона. Запись правила:

а) ;

б) .

3. Правило расширения. Правило записывается в следующем виде:

.

4. Правило склеивания. Базируется на понятии соседних конъюнкций. Соседними называются конъюнкции, отличающиеся представлением одной переменной. Например, конъюнкции и , и являются попарно соседними. В первой паре конъюнкции отличаются представлением х ₂ , а во второй – представлением х₁ . По этим переменным конъюнкции склеиваются.

Формулировка правила: две соседние конъюнкции склеиваются с образованием одной конъюнкции меньшего ранга; исчезает та переменная, по которой конъюнкция склеивается.

, .

Контрольные вопросы

1. Перечислите основные законы алгебры логики. Как дозывается их справедливость?

2. Перечислите следствия из законов алгебры логики.

3.5 Логические функции многих переменных

Все логические операции, которые были рассмотрены в 3.2, распространяются и на функции нескольких переменных. Теперь будем рассматривать функции F ( x ₁ , x ₂ ,…, x_n ) , где x_i – логические переменные, которые принимают значения нуля или единицы. Для описания логики функционирования аппаратных и программных средств компьютера используется алгебра логики, или булева алгебра. Два элемента алгебры логики – ее константы – 0 (ложь) и 1 (истина). Во всех компьютерах используются сигналы двух видов. Сигналы можно интерпретировать как двоичные числа, или логические переменные.

Логической функцией F от набора логических переменных х₁ ,…, х _n называется функция, которая может принимать только два значения: логический 0 и логическая 1.

Область определения логической функции конечна и зависит от количества возможных наборов аргументов. Если n – число аргументов, то количество возможных наборов аргументов равно 2 n .

Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записываются наборы аргументов, а в правой – соответствующие значения функции.

A	B	AB				(AB) ()

x1	x2	…	xn-1	xn	F(x1, x2,… , xn-1, xn )
0	0	…	0	0	F (0,0,…, 0,0)
0	0	…	0	1	F (0,0,…, 0,1)
0	0	…	1	0	F (0,0,…, 1,0)
…	…	…	…	…	…
1	1	…	1	1	F (1,1,…, 1,1)

Вектором значений булевой функции F ( x ₁ ,…, x_n ) называется упорядоченный набор всех значений функции F , при которых значения упорядочены по лексикографическому порядку множества аргументов n .

Поскольку всего имеется 2 n наборов нулей и единиц (| n |=2 n ), существует ровно булевых функций F ( x ₁ ,…, x_n ) от n переменных:

.

При n =2 количество функций равно 16, при n =3 – 256 и т. д. На рис. 3 представлены в упорядоченном виде наборы аргументов для ряда функций – отрицания 0, функций одного, двух и трёх аргументов.

Рис. 3. Упорядоченные наборы аргументов

Пусть F – двоичная функция от n переменных. Предположим, что F не равна тождественно нулю. Пусть T ₁ , T ₂ , …, T_k – все точки ее определения, в которых F =1. Можно доказать, что справедлива следующая формула:

,

где , j=1,2,…, k,

Построить функцию F можно и по-другому. Если функция F не равна тождественно единице и S ₁ , S ₂ ,…, S_m – все точки области ее определения, в которых F =0, то справедлива формула:

,

где , j =1,2,…, m .

Из приведенных формул видно, что любую двоичную функцию можно записать, используя лишь операции ¬, , .

Основная конъюнкция – это конъюнкция основных высказываний переменных или их отрицаний. Например, .

Основная дизъюнкция – это дизъюнкция основных высказываний переменных или их отрицаний. Например, .

Конъюнктивной нормальной формой (КНФ) данной формулы называется формула, равносильная данной и представленная в виде конъюнкции основных дизъюнкций. Например, ( A + B ) ( A + C + B ) ( D + A ) .

Дизъюнктивной нормальной формой (ДНФ) данной формулы называется формула, равносильная данной и представленная в виде дизъюнкции основных конъюнкций. Например, AB + C + AC .

Теорема 1. Для того чтобы формула алгебры высказываний была тождественно истинной, необходимо и достаточно, чтобы ее КНФ содержала в каждой элементарной дизъюнкции некоторое высказывание и его отрицание.

Теорема 2. Для того чтобы формула алгебры высказываний была тождественно ложной, необходимо и достаточно, чтобы ее ДНФ содержала в каждой элементарной конъюнкции некоторое высказывание и его отрицание.

Совершенные дизъюнктивные, конъюнктивные и полиномиальные нормальные формы представления переключательных (логических) функций. Многообразие формул, посредством которых может быть выражена любая логическая функция, определяет многообразие форм логических функций, т. е. способов их записи путем применения к переменным и их группам элементарных логических операций. Наиболее удобными для практического использования оказываются совершенные нормальные формы представления сложных логических функций. В алгебре логики доказывают, что любая логическая функция F ( A , B , C ,…, N ) может быть представлена только одной совершенной дизъюнктивной нормальной формой (кроме константы нуль) или только одной совершенной конъюнктивной нормальной формой (кроме константы единица).

Пусть функция X = F ( A , B , C ) задана таблицей 4. Запись функции Х в виде логической суммы (дизъюнкции) логических произведений (конъюнкций) переменных, для которых значение функции Х равно 1, и является совершенной дизъюнктивной нормальной формой (СДНФ) представления логической функции.

A	B	C	X
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

СДНФ логической функции следует находить в такой последовательности:

1) составить произведения переменных для строк таблицы истинности, в которых Х равна 1. Если значение переменной (А, В или С ) в строке равно 0, то в произведении записывается отрицание этой переменной;

2) написать сумму произведений, для которых функция Х равна 1. Полученная сумма и является СДНФ. В общем виде

, (1)

Это правило называют правилом записи переключательной функции по единицам. Согласно этому правилу, данные табл. 4 описываются аналитическим выражением, связывающим все наборы переменных, для которых Х =1, в виде:

. (2)

Запись функции Х в виде логического произведения (конъюнкции) логических сумм (дизъюнкций) переменных, для которых функция Х равна 0, является совершенной конъюнктивной нормальной формой (СКНФ) представления логической функции.

Для табл. 4 аналитическое выражение в СДНФ, связывающее все наборы переменных, для которых Х =0, имеет вид:

. (3)

Для представления логической функции Х в СКНФ произведем операцию отрицания левой и правой частей равенства (3)

и на основании законов двойного отрицания и инверсии

. (4)

СКНФ логической функции, согласно (4), следует находить в такой последовательности:

1) составить логические суммы переменных для строк таблицы истинности, в которых функция Х равна 0. Если значение переменной (А, В или С ) в строке равно 1, то в сумме записывается отрицание этой переменной;

2) написать логическое произведение составленных логических сумм. Полученное произведение и является СКНФ. В общем виде:

, (5)

где F_i – сложные дизъюнкции.

Это правило также называют правилом построения переключательной функции по нулям.

Кроме представления функций в виде СДНФ и СКНФ используют и совершенную полиномиальную нормальную форму СПНФ. Вместо дизъюнкции может быть записана функция сложения по модулю два (сумма Жегалкина):

, (6)

где F_i – сложные конъюнкции.

Существует специальная таблица, в которой все элементарные логические операции от двух аргументов представлены в двух совершенных нормальных формах.

Нормальные формы представления переключательной функции иногда называют стандартными (табл. 5).

Название функцииОбозначение функцииСДНФСКНФf₀0000Константа нуль0Не имеетf₁0001Логическое произведение, конъюнкцияf₂0010Функция запрета по Вf₃0011Переменная Аf₄0100Функция запрета по Аf₅0101Переменная Вf₆0110Сумма по мо дулю 2, логическая неравнозначностьf₇0111Логическое сложение, дизъюнкцияf₈1000Операция (стрелка) Пирса, операция Веббаf₉1001Эквивалентность, логическая равнозначностьf₁₀1010Инверсия Вf₁₁1011Импликация от В к Аf₁₂1100Инверсия Аf₁₃1101Импликация от А к Вf₁₄1110Операция (штрих) Шеффераf₁₅1111Константа единица1Не имеет

Многочленом Жегалкина называется многочлен, являющийся суммой константы 0 или 1 и различных одночленов, в которые все переменные входят не выше, чем в первой степени.

Теорема. Любая функция булевой алгебры может быть представлена, и притом единственным образом, с помощью полинома Жегалкина вида

J =.

Представим, например, в виде полинома выражение вида X ₁ X ₂ . Для этого проведем следующие рассуждения.

X₁ X₂ = aX₁ X₂ +bX₁ +cX₂ +k,

где а, b , с, k – неопределенные коэффициенты.

X ₁ X ₂ = – X ₁ X ₂ + X ₁ + X ₂ .

СПНФ образуется путем замены в СДНФ: на + и на

1 х.

,

,

В последнем случае выражение для легко можно упростить, если раскрыть скобки и взаимно сократить все одинаковые слагаемые, входящие в формулу четное число раз:

.

Подобное упрощение, которое называется минимизацией логической функции, можно осуществить и по отношению к СДНФ и СКНФ.

			y
0	0	0	0
1	0	0	1
0	1	0	0
1	1	0	1
0	0	1	1
1	0	1	0
0	1	1	0
1	1	1	1

Применение законов алгебры логики позволяет найти более компактные аналитические выражения для заданной функции у , т. е. минимальную дизъюнктивную нормальную форму . Приведем соответствующие формы представления функции у , заданной табл. 6:

,

и для СКНФ, т. е. минимальную КНФ:

.

После того, как найдены минимальные нормальные формы (МНФ), их рекомендуется проверить на всех наборах аргументов . Переменные или часто называют термами. Именно полный набор из n термов образует конституенту. В процессе же минимизации некоторые термы из конституент пропадут. Тогда оставшуюся часть дизъюнкта или конъюнкта называют импликантой.

Как мы только что убедились на примере, импликанты появляются в результате склейки смежных конституент, различающихся одним термом.

Контрольные вопросы и упражнения

2. Что такое вектор значений булевой функции? Приведите пример построения таблицы истинности логической функции многих переменных.

3. Сколько существует булевых функций от n переменных?

4. Что такое ДНФ и КНФ?

5. Каков алгоритм построения СДНФ? Приведите пример построения СДНФ.

6. Каков алгоритм построения СКНФ? Приведите пример построения СКНФ.

7. Составьте СКНФ и СДНФ для функции .

8. Приведите пример построения СПНФ.

3.7 Некоторые замкнутые классы (классы Поста). Понятие базиса

Система булевых функций <f ₁ , f ₂ ,…, f_m > называется полной, если любая булева функция может быть выражена через функции f ₁ , f ₂ ,…, f_m с помощью суперпозиций.

а) переименованием некоторой переменной x_j какой-нибудь функции f_i ;

б) подстановкой некоторой функции вместо какой-либо переменной x_j любой из функций .

Суперпозиции ранга 1 образуют класс функций К 1 . Класс функций, получающийся из функций класса K s -1 суперпозицией ранга s ‑1 с помощью элементарных суперпозиций, называется классом функций K s суперпозиций ранга s . Суперпозициями функций из К 0 называются функции, входящие в какой-то из классов K s .

Согласно введенным определениям, можно говорить, что система булевых функций полна. Тогда любую булеву функцию можно представить в виде многочлена от своих переменных.

В современном компьютере цифрами являются ноль и единица. Следовательно, команды, которые выполняет процессор, суть булевы функции. Мы уже видели, что любая булева функция реализуется через конъюнкцию, дизъюнкцию и отрицание. Следовательно, можно построить нужный процессор, имея в распоряжении элементы, реализующие . Далее рассмотрим вопрос: существуют ли (и если существуют, то какие) другие системы булевых функций, обладающие тем свойством, что с их помощью можно выразить все другие функции. Рассмотрим некоторые замкнутые классы (классы Поста), их пять.

1. Класс функций, сохраняющих константу нуль (обозначается T₀ или P₀ ):

К этому классу относятся, например, функции ; ; ; .

2. Класс функций, сохраняющих константу единица (обозначается T₁ или P₁ ):

К нему относятся все нечетные функции.

3. Класс самодвойственных функций (обозначается T_* или S):

Пример и .

Функция называется двойственной по отношению к функции , если . Двойственная функция получается из исходной при замене значений всех переменных, а также значений функции на противоположные, т. е. в таблице истинности нужно заменить 0 на 1, 1 на 0.

Пример. Двойственной к функции является функция, соответствующая формуле , т. е. или : . Аналогично , .

Если ,

то .

Таким образом, функция, двойственная суперпозиции функций, есть соответствующая суперпозиция двойственных функций.

Этот принцип удобен при нахождении двойственных функций, представленных формулами, содержащими лишь конъюнкции, дизъюнкции и отрицание. В этом случае в исходной формуле конъюнкции заменяются на дизъюнкции, а дизъюнкции – на конъюнкции. Таким образом, ДНФ соответствует КНФ, КНФ – ДНФ, СДНФ – СКНФ, СКНФ – СДНФ.

Пример. ,

если , то и .

Функция называется самодвойственной, если .

Пример. Покажем, что формула задает самодвойственную функцию.

Убедимся, что на всех противоположных наборах значений переменных и формула принимает противоположные значения. Действительно, составим таблицу истинности:

	x	y	z
0	0	0	0
0	0	0	1
0	0	1	0
1	0	1	1
0	1	0	0
1	1	0	1
1	1	1	0
1	1	1	1

Получаем , , , .

4. Класс монотонных функций (обозначается T_M или M):

, где , , , .

5. Класс линейных функций (обозначается T_L или L):

.

Эквивалентность является линейной функцией . Стрелка Пирса – нет, .

, , ,…, ,

, ,…, . (7)

Таким образом, проверка линейности сводится к нахождению коэффициентов по формулам (7) и сопоставлению таблиц истинности данной формулы и полученной формулы .

Пример. Проверим, является ли линейной функция . Имеем , , . Таким образом, . Сопоставляя таблицы истинности формул и , убеждаемся, что они не совпадают. Вывод: функция нелинейна.

Линейность функции можно также определить с помощью следующей теоремы.

Теорема Жегалкина. Всякая булева функция представима полиномом Жегалкина, т. е. в виде , где в каждом наборе (i ₁ ,…, i_k ) все i_j различны, а суммирование ведется по некоторому множеству таких несовпадающих наборов. Представление булевой функции в виде полинома Жегалкина единственно с точностью до порядка слагаемых.

Полином Жегалкина называется нелинейным (линейным), если он (не) содержит произведения переменных.

Таким образом, линейность булевой функции равносильна линейности соответствующего полинома Жегалкина.

Для получения полинома Жегалкина булевой функции, находящейся в СДНФ, используются аксиомы булевой алгебры, аксиомы булева кольца и равенства, выражающие операции через операции этого булева кольца: и т. д.

Пример. Определим линейность функции .

Полученный полином Жегалкина является нелинейным, и, следовательно, функция f также нелинейна.

Заметим, что если в эквивалентности формулы являются различными конституентами единицы, то их произведение равно 0, и тогда . Следовательно, для получения полинома Жегалкина из СДНФ можно сразу заменить .

Отметим, что каждый класс Поста замкнут относительно операций замены переменных и суперпозиции, т. е. с помощью этих операций из функций, принадлежащих данному классу, можно получить только функции из этого же класса.

Пример. Определим, к каким классам Поста относится булева функция .

Так как f (0,0)=1, а f (1,1)=0, то и . Поскольку , то . Так как f (0,0)>f (1,1), то . Полином Жегалкина для функции имеет вид в силу равенства . Поэтому данная функция нелинейна. Таким образом, можно составить следующую таблицу

Функция	Классы
	Р0	Р1	S	М	L
х | у	Нет	Нет	Нет	Нет	Нет

Теорема Поста. Система F булевых функций тогда и только тогда является полной, когда для каждого из классов P ₀ , P ₁ , S , M , L в системе F найдется функция, не принадлежащая этому классу.

В силу теоремы Поста функция х | у образует полную систему, т. е. с помощью штриха Шеффера можно получить любую булеву функцию. В частности, .

Система булевых функций называется базисом , если она полна, а удаление любой функции из этой системы делает ее неполной.

Теорема. Каждый базис содержит, не более четырех булевых функций.

Доказательство. Предположим, что существует базис F , состоящий более чем из четырех функций. По теореме Поста тогда получаем, что F состоит ровно из пяти функций, каждая из которых не принадлежит ровно одному классу Поста. Пусть f – функция из F , не принадлежащая классу Р₀ . Тогда, с одной стороны, f (0,0,…, 0) =1, а, с другой – из следует, что f (1,1,…, 1) =1. Это означает, что f не является самодвойственной функцией, что противоречит предположению.

Пример. Следующие системы булевых функций являются базисами: .

;

следовательно,

;

следовательно,

;

следовательно, ;

;

следовательно, ;

Обоснование	Базис
– конъюнктивный базис
– дизъюнктивный базис
;	<И, , 1> – базис Жегалкина
– базис Шеффера
<> – базис Пирса

Конъюнкции, то есть все функции вида , тоже составляют замкнутый класс. Очевидно, однако, что, например, функцию, которая на наборе (0,0,…, 0) имеет значение 1, нельзя представить суперпозицией таких функций. Таким образом, не является базисом, следовательно, конъюнктивный базис является минимальным.

Рассмотрим более подробно базис Жегалкина.

Алгебра Жегалкина и линейные функции

Алгебра Жегалкина – это алгебра над множеством двух бинарных булевых функций (И, ) и нульарной функции 1. Легко проверить следующие соотношения в этой алгебре:

;

;

;

.

Если в произвольной формуле, включающей только функции базиса Жегалкина, раскрыть скобки, то получим бесскобочную формулу, имеющую вид суммы (по модулю два) произведений, то есть некоторый полином. Он называется полиномом Жегалкина.

Широкий набор базисов открывает большие возможности при решении задач минимизации схем устройств дискретного действия, поскольку из базисных схем с помощью суперпозиций можно составить схему, соответствующую любой булевой функции.

Контрольные вопросы и упражнения

1. Дайте определение полной системе булевых функций.

2. Перечислите классы Поста.

3. Дайте определение двойственной функции. Приведите примеры.

4. Дайте определение самодвойственной функции. Приведите примеры.

5. Постройте полином Жегалкина для функции «стрелка Пирса».

6. Сформулируйте теорему Поста.

7. Что такое базис? Приведите примеры базисов.

3.8 Методы минимизации логических функций

Наиболее употребляемая операция при минимизации функций – это операция склеивания.

Рассмотрим три наиболее распространенных метода минимизации.

1. Пусть будут заданы номера наборов четырех переменных, на которых логическая функция принимает единичное значение: f (2,5,6,7,10,12,13,14) =1.

Выразим эту логическую функцию в СДНФ (символ конъюнкции писать не будем):

f (0010,0101, 0110, 0111, 1010, 1100, 1101, 1110) =

.

На первом этапе минимизации исходную СДНФ можно упростить за счет использования закона склеивания, тогда получим:

.

Обращаем внимание на то, что одну и ту же конституенту (импликанту) можно склеивать с другими конституентами (импликантами) многократно, так как в логике Буля действует закон идемпотентности:

,

поэтому любую конституенту можно размножить.

На втором этапе воспользуемся таблицей Куайна (табл. 8), в соответствии с которой данный метод минимизации получил свое наименование – метод Куайна. В таблице по вертикали перечислены все полученные на первом этапе упрощения импликанты, а по горизонтали – исходные конституенты. Единица в табл. 8 стоит там, где импликанта «накрывает» конституенту. Дело в том, что конституента всегда может быть заменена импликантой или даже отдельным термом по закону поглощения:

	0010	0101	0110	0111	1010	1100	1101	1110
– – 1 0	1	0	1	0	1	0	0	1
01–1	0	1	0	1	0	0	0	0
01 1 –	0	0	1	1	0	0	0	0
– 1 0 1	0	1	0	0	0	0	1	0
1 1 0 –	0	0	0	0	0	1	1	0
11–0	0	0	0	0	0	1	0	1

После заполнения таблицы Куайна у нас получилось так, что почти в каждой графе оказалось по две единицы; между тем достаточно иметь одну единицу в графе. Поэтому, по возможности, нужно исключить избыточные единицы. Выбор единиц производится из соображений минимальности числа термов (выбранные единицы затемнены). В итоге оказалось, что можно обойтись только тремя импликантами вместо шести:

.

С помощью таблиц истинности легко проверить, что полученная в МНФ функция воспроизводит все значения исходной функции. Отметим, что в общем случае решений по критерию минимума термов может быть несколько.

2. Не менее эффективным способом минимизации логических функций является метод сочетания индексов. Для его изложения составим табл. 9, в графах которой записаны возможные сочетания индексов. В последней графе выписаны значения функции. Анализ таблицы начинается слева по столбцам. Принцип исключения i , j ‑кода следующий. На пересечении i ‑столбца, например, с сочетанием индексов 23, и j ‑строки, например, 3‑ей, находится код 10, что соответствует импликанте . Следовательно, в этом столбце везде, где встречается код 10, т. е. в строках 2, 3, 10 и 11, эти коды исключаются, поскольку значение функции в 3‑ей строке равно нулю. Теперь возьмем столбец с сочетанием индексов 124. Здесь во 2‑ой и 6‑ой строках оставлены коды 010, а в 10‑ой и 14‑ой строках – код 011. Сделано это потому, что эти коды встречаются только на строках со значением функции, равным единице. Напротив, код 110 этого же столбца встречается как при единичных значениях функции, так и при нулевых.

n	1	2	3	4	12	13	14	23	24	34	123	124	134	234	1234	y
0	0	0	0	0	00	00	00	00	00	00	000	000	000	000	0000	0
1	1	0	0	0	10	10	10	00	00	00	100	100	100	000	1000	0
2	0	1	0	0	01	00	00	10	10	00	010	010	000	100	0100	1
3	1	1	0	0	11	10	10	10	10	00	110	110	100	100	1100	0
4	0	0	1	0	00	01	00	01	00	10	001	000	010	010	0010	0
5	1	0	1	0	10	11	10	01	00	10	101	100	110	010	1010	1
6	0	1	1	0	01	01	00	11	10	10	011	010	010	110	0110	1
7	1	1	1	0	11	11	10	11	10	10	111	110	110	110	1110	1
8	0	0	0	1	00	00	01	00	01	01	000	001	001	001	0001	0
9	1	0	0	1	10	10	11	00	01	01	100	101	101	001	1001	0
10	0	1	0	1	01	00	01	10	11	01	010	011	001	101	0101	1
11	1	1	0	1	11	10	11	10	11	01	110	111	101	101	1101	0
12	0	0	1	1	00	01	01	01	01	11	001	001	011	011	0011	1
13	1	0	1	1	10	11	11	01	01	11	101	101	111	011	1011	1
14	0	1	1	1	01	01	01	11	11	11	011	011	011	111	0111	1
15	1	1	1	1	11	11	11	11	11	11	111	111	111	111	1111	0

Итак, все коды на строках, заканчивающихся нулевыми значениями функции, исключаются автоматически. Если эти коды попадают на строки, заканчивающиеся единичным значением функции, то они также не учитываются. Остаются только те коды, которые расположены на строках с единичным значением функции (эти коды затемнены).

Далее руководствуются следующим правилом. Для того чтобы функция приняла значение, равное единице, достаточно того, чтобы только какая-нибудь одна импликанта на строке приняла единичное значение. Прежде всего, оставляем минимальную импликанту , которая перекрывает единицы в строках 2, 6, 10 и 14. Затем, естественно, обращаемся к 12‑ой строке. Здесь оставляем единственный на строке код 011, что отвечает импликанте . Эта же импликанта ответственна за 13‑ую строку, оканчивающуюся тоже единицей. Осталось рассмотреть 5‑ую и 7‑ую строки. Общей для них является импликанта: . Таким образом, тремя импликантами мы перекрыли все единичные значения функции, что совпадает с результатом, полученным на основе таблиц Куайна.

3. Существует графический способ склеивания, который получил название метод карты Карно (представлен в табл. 10). Выделяем смежные единицы, это и будут слагаемые нашей функции.

00011110000011011000111000100000

– получили два слагаемых

Хотя табл. 9 более громоздка, чем табл. 8, метод сочетания индексов не считается более сложным, чем метод Куайна, если помнить, что до составления таблиц Куайна необходимо произвести многочисленные склейки конституент и импликант. Реализация на компьютере алгоритма метода сочетания индексов оказывается сравнительно простой. И напротив, внешняя простота и наглядность третьего метода минимизации логических функций с помощью карт Карно оборачивается сложной программой при реализации алгоритма на компьютере.

	1100	1110	0110	0100
	1101	1111	0111	0101
	1001	1011	0011	0001
	1000	1010	0010	0000

Карта Карно для четырех переменных представлена в виде табл. 11. Каждая клетка карты соответствует конституенте. Заполненная карта представлена табл. 12 (функция взята та же, что и в первых двух методах). Согласно закону склеивания, две смежные конституенты с единичными значениями всегда можно объединить для получения соответствующей импликанты. Причем смежными считаются и те, которые лежат на границах карты. Какие именно единицы требуется объединить для получения подходящей импликанты, легко определить визуально. Следует также помнить, что в соответствии с законом идемпотентности одна и та же единица табл. 12 может склеиваться с двумя или тремя смежными единицами.

Контрольные вопросы

1. Перечислите основные методы минимизации функций.

2. Расскажите о методе Куайна.

3. Расскажите о методе карт Карно.

3.9 Неполностью определенные логические функции

Ранее мы рассматривали ситуации, когда на множество аргументов или логических переменных x ₁ , x ₂ ,…, x_n не накладывались ограничения, или, что то же самое, функции были определены на всем наборе аргументов. Однако реально на практике функции либо не определены полностью, либо есть запрещенные комбинации. Необходимо доопределить функцию таким образом, чтобы аналитическая форма ее представления была минимальной, далее производят склейки (пример приведён в табл. 13).

000*01*0011*111*110010*100*0*1*0*

.

* – эти значения доопределили сами, исходя того, чтобы выражение для функции F было минимальным.

3.10 Формы представления булевых функций

К настоящему времени мы знакомы с двумя формами представления булевых функций: таблица истинности и формула (аналитическая запись). Рассмотрим еще две формы представления таких функций.

3.10.1 Семантические деревья

Семантическое дерево – это двоичное дерево, корень которого помечен двоичной функцией от m переменных, из каждого узла идут по два ребра, соответствующих двум значениям очередной переменной, а 2 m листьев помечены соответствующими значениями функции.

3.10.2 Бинарные диаграммы решений (БДР )

Бинарная диаграмма решений (BinaryDecisionDiagrams, BDD) – это граф, являющийся модификацией семантического дерева. В БДР узлы с одним и тем же значением функции объединены. Если на каждом уровне БДР все вершины имеют одну и ту же метку (одинаковые переменные), то такая БДР называется упорядоченной (в англоязычной литературе такое представление называется OrdinaryBinaryDecisionDiagrams, или сокращенно OBDD). Будем называть такое представление УБДР. Вершины УБДР расположены по уровням, каждому уровню соответствует одна переменная, которая помечает вершины, находящиеся на этом уровне. Из каждой вершины выходят два ребра: одно соответствует нулевому значению соответствующей переменной (будем его изображать штриховой линией), а другое – единичному значению этой переменной (оно изображается сплошной линией).

На рис. 4 показаны все четыре формы представления функции .

Бинарные диаграммы решений используются как компактная форма представления булевой функции. Такое представление полезно во многих случаях, например, когда нужно многократно вычислять значения функции при различных наборах значений ее аргументов. Для того чтобы получить значение функции f , например, на языке С, вместо хранения громоздкой таблицы истинности можно вычислить оператор: f = q ? ( r ? 0:1): (р? 0:1) , который построен на основании БДР (см. рис. 4). В этом примере использование УБДР позволяет вычислить значение булевой функции, выполнив всего две операции, в то время как при ее вычислении по аналитическому представлению требуется не менее 5 операций.

Рис. 4. Четыре формы представления двоичной функции

f (p, q, r)	Таблица истинности	Семантическое дерево	Бинарная диаграмма решений
p q r f 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 0

Сложность представления функции с помощью УБДР существенно зависит от порядка переменных. Так, например, УБДР для иного порядка переменных, чем на рис. 4, содержит четыре вершины, а не три (рис. 5). Интересной проблемой теоретической информатики является нахождение алгоритма, дающего оптимальный порядок переменных булевой функции с точки зрения представления этой функции упорядоченной БДР.

Рис. 5. УБДР для функции с порядком переменных [p , q , r ]

3.11 Построение логических схем

При синтезе логических схем применяют элементы с одним и несколькими входами. Условия функционирования таких элементов определяются переключательными функциями одной или нескольких переменных.

Входные и выходные сигналы логических схем зависят от времени (одни из них в некоторый момент времени равны 1, в другие моменты времени 0). Логические функции, описывающие работу таких схем, называют переменными . Используют также схемы, для которых во все моменты времени сигналы равны либо 1, либо 0. Логические функции, описывающие работу этих схем, называют постоянными .

Существует только четыре различные переключательные функции одной переменной. Как видно из таблицы 14, только две функции не зависят от переменной А (в этих случаях переменная А фиктивна).

Для функции двух переменных существует шестнадцать различных переключательных функций. Как видно из таблицы 5, только десять функций существенно зависят от переменных А и В .

На рис. 6, 7 приведены обозначения элементов, реализующих некоторые переключательные функции двух переменных.

Каждой элементарной логической операции можно поставить в соответствие элементарную логическую схему или вентиль. На входе и выходе вентиля мы имеем логические сигналы двух видов, что можно ассоциировать с логическим 0 или логической 1.

1. Элемент «И» 2. Элемент «ИЛИ» 3. Элемент «НЕ»

F=x₁ ∙x₂ F=x₁ x₂ F=

Рис. 6. Символическое обозначение вентилей

г) д ) е )

Рис. 7. Условные обозначения переключательных функций двух переменных: а – элемент Шеффера; б – элемент Пирса; в-импликатор; г – запрет; д – равнозначность; е – сложение по модулю 2

В технической литературе используются обозначения элементов, несколько отличающихся друг от друга.

Логическая схема, которая полностью описывается булевыми выражениями или таблицами истинности, называется комбинационной схемой.

Таким образом, комбинационная схема – схема, в которой значения входных переменных в текущий момент времени полностью определяют значения выходных переменных.

Другой класс схем – последовательностные схемы. Это схемы с внутренней памятью. В них значения выходных переменных определяются не только значениями входных переменных в текущий момент времени, но и их значениями в предыдущие моменты времени.

Будем рассматривать только комбинационные схемы.

До сих пор мы рассматривали поведение логической схемы, таблицы истинности и булевы выражения, использованные для описания значений выходной переменной в зависимости от набора значений входных переменных. Но булево выражение содержит сведения и о структуре логической схемы.

Соединив логические элементы в соответствии с булевыми выражениями, получим логическую схему, реализующую данное выражение.

Логическая связь выхода и входов этой схемы описывается исходным булевым выражением. Таким образом, булево изображение – описание логической схемы.

Контрольные вопросы

1. Перечислите все известные формы представления булевых функций.

2. Перечислите основные элементы, используемые при построении логических схем.

3.12 Логические конечные автомат ы

3.12.1 Процессы

Описывая конкретные алгоритмы, мы отмечали, что вычисление по алгоритму можно рассматривать как некоторый процесс, который описывается множеством состояний, начальным состоянием и правилами перехода из состояния в состояние.

Рассмотрим три варианта таких правил и соответственно три в принципе различных процесса:

· процесс, в котором переходы выполняются под влиянием некоторых внешних воздействий. Этот процесс называется автоматом;

· процесс, в котором переходы выполняются под влиянием некоторого случайного механизма. Таких процессов можно придумать много, простейший из них, который будем рассматривать в дальнейшем, называется марковской цепью;

· процесс, в котором переходы выполняются по выбору некоего «одушевленного существа», стремящегося выбрать такой набор или последовательность решений, которые обеспечат ему максимальное значение некоторой функции от траектории процесса. Это управляемые процессы.

Разумеется, кроме таких чистых схем имеются и всякого рода смеси. Однако, чистые схемы интересны тем, что по ним можно увидеть, на что в соответствующей конкретной науке обращается особое внимание, и как сильно традиции этой конкретной науки влияют на изучение одного и того же математического объекта.

3.12.2 Конечные автоматы

М – конечное непустое множество, элементы которого называются состояниями автомата;

А – конечное непустое множество внешних воздействий на автомат (входной алфавит автомата);

В-множество ответов автомата на внешние воздействия (выходной алфавит).

Автомат – это процесс, который рассматривается в дискретные моменты времени (такты работы) и в каждый момент времени получает внешние воздействия. В зависимости от воздействия и текущего состояния процесса переходит в новое состояние и вырабатывает свой ответ.

По сравнению со схемой из функциональных элементов конечный автомат является более точной моделью дискретного преобразователя информации, однако, как и любая модель, понятие конечного автомата связано с рядом упрощающих предположений.

Во-первых, предполагается, что вход (выход) автомата в каждый момент времени может находиться в одном из конечного числа различных состояний. Но у реального преобразователя входной сигнал x ( t ) представляет собой непрерывную величину, и для описания такого преобразователя с помощью модели конечного автомата нужно разделить диапазон изменения x ( t ) на конечное число уровней и произвести квантование.

Во-вторых, предполагается, что время изменяется дискретно. Это означает, что состояния входа и выхода устройства отмечаются только в определенные моменты времени, образующие дискретную последовательность

t ₁ , t ₂ ,…, t_n . Каждый момент времени однозначно определяется его индексом, поэтому с целью упрощения будем считать, что время t принимает значения 1, 2, 3,…, n . Промежуток (n , n +1 ) называется тактом.

Конечный автомат является математической моделью реальных дискретных устройств по переработке информации. Структура теории конечных автоматов определяется теми задачами, которые возникают при производстве и эксплуатации таких устройств.

Теория автоматов – раздел теоретической кибернетики, в котором изучаются математические модели (называемые автоматами, машинами) реально существующих (механических, биологических и т. п.) или принципиально возможных устройств, перерабатывающих дискретную информацию дискретными временными тактами.

Теория автоматов возникла, главным образом, под влиянием запросов техники цифровых вычислительных и управляющих машин, а также внутренней потребности теории алгоритмов и математической логики.

Понятие «автомата» заметно варьируется в зависимости от характера названных устройств, от принятого уровня абстракции и целесообразной степени общности (автоматы конечные, бесконечные, растущие, вероятностные, детерминированные, автономные и т. п.).

Автомат можно рассматривать как частный случай общего понятия управляющей системы. В теории автоматов широко применяется аппарат алгебры, математической логики, комбинаторного анализа (включая теорию графов) и теорию вероятностей.

Конечные и бесконечные автоматы характеризуются соответственно конечностью и бесконечностью объема памяти (число внутренних состояний). Конечными автоматами являются отдельные блоки компьютера и даже компьютер в целом. Мозг тоже можно также рассматривать как конечный автомат. Бесконечные автоматы представляют собой естественную математическую идеализацию, вырастающую из представления об автомате с конечным, но необратимо большим числом состояний.

Анализ автоматов – нахождение по заданному в том или ином виде автомату отображения «вход-выход», осуществляемого этим автоматом; часто такое отображение можно интерпретировать как вычисление предиката, и поскольку каждый предикат характеризуется своим множеством истинности, то задача анализа автомата сводится к нахождению этого множества (говорят, что это множество распознается автоматом).

Для многих классов автоматов хорошо известны классы распознаваемых ими множеств. Например, машины Тьюринга распознают все рекурсивно перечислимые множества, автоматы с магазинной памятью (недетерминированные) – контекстно свободные языки.

Далеко не всегда по заданным автомату и множеству удается определить, распознает ли автомат в точности это множество. В общем виде для произвольного класса автоматов или даже для произвольного конкретного автомата эта проблема является алгоритмически неразрешимой. Если наложить ограничения на способы задания автоматов и на способы задания множеств, то для многих случаев она становится разрешимой. Например, если регулярные события задавать регулярными выражениями, а конечные автоматы – матрицами переходов и выходов, то существует общий конструктивный прием (алгоритм анализа конечных автоматов), позволяющий находить регулярные выражения для событий, представляемых в произвольном конечном автомате.

Синтез автоматов – построение автоматов по заданному поведению «вход-выход». Проблема синтеза наиболее подробно исследовалась для конечных автоматов, поскольку к этому случаю сводятся многие практические задачи, связанные с проектированием разного рода управляющих и вычислительных устройств.

Трудности синтеза автоматов зависят в основном от того, как заданы условия функционирования автомата. Чем выразительнее язык, применяемый для задания условий функционирования аппарата (т. е., чем удобнее он для заказчика), тем сложнее метод синтеза. Во многих случаях может оказаться, что единого метода синтеза не существует. Поэтому для ряда классов автоматов, в частности, для конечных автоматов, разрабатываются специальные языки, с помощью которых удобно задавать условия функционирования автоматов, для которых существуют методы синтеза (регулярные событияи выражения, логический язык для задания автоматов).

Минимизация числа состояний автомата – по произвольному заданному конечному автомату создается автомат с наименьшим возможным числом состояний, обладающий тем же поведением, что и исходный автомат. Решение этой задачи состоит в нахождении эффективного алгоритма минимизации. Оно представляет интерес, как в абстрактной теории автоматов, так и в проектировании реальных автоматов.

Рассмотрим модели, которые представлены в виде некоторого черного ящика, на вход которого поступают некоторые логические переменные x₁ , x₂ ,…, x_n . Объект их перерабатывает, и на выходе получаем некоторые логические функции y₁ , y₂ ,…, y_k .

Рис. 8. Логический конечный автомат

Такие модели называют логически конечными автоматами. Существуют некоторые классы таких автоматов:

— автоматы без памяти (комбинационные)

— автоматы с памятью (последовательностные).

Общая формула, описывающая этот вид автоматов:

, i = 1, 2, …, k.

– в векторной форме

Примером таких автоматов является простая экспертная система профессиональной пригодности, где входные значения – это ответы на n вопросов, а выходные – k выводов о том, может ли человек работать в данной области.

Диагностика неисправностей, заболеваний и т. д.

Пусть функционирование логического автомата описывается формулой:

.

На языке Pascal оператор присваивания, соответствующий этой формуле:

Для более сложной модели получается структура типа запись:

Далее моделируется базис, который будет работать с этими высказываниями. Для каждой логической операции пишем процедуру или функцию.

Functionotr (a: prep; varb: prep; параметры сохранения и т. д.): Boolean;

Function con (a, b: prep; var c: prep; параметрысохраненияи т. д.): Boolean;

Function diz (a, b: prep; var c: prep; параметрысохраненияи т. д.): Boolean;

Отмоделировать функцию Y_i :

Function y1 (x₁ , x₂ , x₃ , x_4: prep; var rez: prep; sohr: Boolean; newnumber: Integer; t: String): Boolean;

I: boolean; a, b, c, d, e,: prep;

I:= con (a, b, c, false, 0);

I:= con (c, x₃ , d, false, 0);

I:= con (c, b, e, false, 0);

I:= diz (d, e, rez, false, 0);

If sohr then begin

Отмоделировать функцию лучше программным путем, т. к. программу довольно просто модифицировать.

3.12.2.2 Конечные автоматы с памятью (последовательностные)

Для таких автоматов характерно наличие вектора внутренних состояний z=(z₁ , z₂ ,…, z_{m ).}

В таких автоматах каждая логическая функция зависит от входных функций x и функций внутреннего состояния z.

Рис. 10. Конечный автомат с памятью

. (8)

Для автоматов с памятью характерно, что они функционируют во времени, и в момент времени t₀ должно быть задано начальное состояние z₀ . В момент времени t₀ определяется выражением (8). В момент времени t₁ =t₀ +tвходной вектор может поменяться, в свою очередь может поменяться вектор состояний Y.

, (9)

где t– такт логического конечного автомата. Считается, что t много больше времени расчета на ЭВМ.

Та же самая экспертная система определения профессиональной пригодности, но с условием, что значение о профессиональной пригодности зависит от ранее полученных ответов. Такие экспертные системы называют самообучающимися, т. к. сразу правильного ответа не дают. Частным случаем конечного автомата с памятью является автомат с обратной связью по выходу. Для него вектор внутренних состояний в момент времени t+t равен вектору выходных сообщений в момент времени t. Пример конечного автомата с памятью и обратной связью по выходу приведен на рис. 11.

Рис. 11. Конечный автомат с памятью и обратной связью по выходу

Экспертная система является примером конечного автомата с памятью с обратной связью по выходу. Программная модель такого автомата базируется на программной модели автомата без памяти, однако, помимо уже накопленного опыта добавляется процедура tact, а также начальные значения входных и выходных переменных.

Vector x = array [1..n] of boolean;

Vector y = array [1..k] of boolean;

Ypred, Y: vector Y;

Procedure tact (v: vector X; var Ypred, Y: vector Y);

Х	А	Условное обозначение	Название функции
	0 1