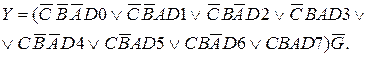Мультиплексоры и демультиплексоры
Цель работы: практическое освоение принципов построения мультиплексоров и демультиплексоров и экспериментальное их исследование на лабораторном стенде.
Мультиплексор – это комбинационная многовходовая схема с одним выходом. Входы мультиплексора подразделяются на информационные Д0, Д1, …, Дn-1 и управляющие (адресные) А0, А1, …, Аk-1. Обычно 2k = n, где k и n – число адресных и информационных входов соответственно. Двоичный код, поступающий на адресные входы, определяет (выбирает) один из информационных входов, значение переменной с которого передается на выход y, т. е. мультиплексор реализует функцию:
, если 
(1)
Таблица функционирования, описывающая работу мультиплексора, имеющего, например, n = 4 информационных (Д0, Д1, Д2, Д3) и k = 2 адресных (А0, А1) входов, представлена в табл. 1.
Вариант схемной реализации мультиплексора “4-1” (“четыре в один”, т. е. коммутирующего данные от одного из четырех входов на единственный выход) и его условное графическое изображение представлены на рис. 1.
Здесь мультиплексор построен как совокупность двухвходовых конъюкторов данных (их число равно числу информационных входов), управляемых выходными сигналами дешифратора, дешифрирующего двоичный адресный код. Выходы конъюкторов объединены схемой ИЛИ.
Рис. 1. Схема мультиплексора с дешифратором (а)
и и его условное графическоеизображение
В интегральном исполнении применяется более простая схема, в которой конъюкторы дешифратора одновременно выполняют и функцию конъюкторов данных. Работа мультиплексора при этом описывается соотношением
(2)
Из (2) следует, что при любом значении адресного кода все слагаемые, кроме одного равны нулю. Ненулевое слагаемое равно Дi, где i – значение текущего адресного кода.
В соответствии с этим соотношением строятся реальные схемы мультиплексоров, одна из которых для мультиплексора “четыре в один” приведена на рис. 2. Как правило, схема дополняется входом разрешения работы – Е (показан пунктирной линией). При отсутствии разрешения работы (Е=0) выход у становится нулевым и не зависит от комбинации сигналов на информационных и адресных входах мультиплексора.
Мультиплексоры 4-1, 8-1, 16-1 выпускаются в составе многих серий цифровых интегральных схем и имеют буквенный код КП. Например, К555КП1 – мультиплексор 2-1 (в данном корпусе размещаются четыре мультиплексора), К555КП12 – мультиплексор 4-1 (в одном корпусе размещаются два мультиплексора) и т. д.
В тех случаях, когда функциональные возможности ИС мультиплексоров не удовлетворяют разработчиков по числу информационных входов, прибегают к их каскадированию с целью наращивания числа входов до требуемого значения. Наиболее универсальный способ наращивания размерности мультиплексора состоит в построении пирамидальной структуры, состоящей из нескольких мультиплексоров. При этом первый ярус схемы представляет собой столбец, содержащий столько мультиплексоров, сколько необходимо для получения нужного числа информационных входов. Все мультиплексоры этого столбца коммутируются одним и тем же адресным кодом, составленным из соответствующего числа младших разрядов общего адресного кода. Старшие разряды адресного кода используются во втором ярусе, мультиплексор которого обеспечивает поочередную работу мультиплексоров первого яруса на общий выход.
Пирамидальная схема, выполняющая функцию мультиплексора “16-1” и построенная на мультиплексорах “4-1”, показана на рис. 3.
Демультиплексор – схема, выполняющая функцию, обратную функции мультиплексора, т. е. это комбинационная схема, имеющая один информационный вход (Д), n информационных выходов (у0, у1, …, уn-1) и k управляющих (адресных) входов (А0, А1, …, Аk-1). Обычно, также как и мультиплексоров, 2k = n. Двоичный код, поступающий на адресные входы, определяет один из n выходов, на который передается значение переменной с информационного входа (Д), т. е. демультиплексор реализует следующие функции:
Таблица функционирования демультиплексора, имеющего n = 4 информационных выходов (у0, у1, у2, у3) и k = 2 адресных входов (А0, А1), представлена в табл. 2.
Уравнения, описывающие работу демультиплексора:
(4)
Схема демультиплексора, построенная по данным уравнениям и его графическое изображение представлены на рис. 4.
Рис. 4. Схема демультиплексора «1-4» (а)
и его условное изображение (б)
Функция демультиплексора легко реализуется с помощью дешифратора, если его вход “Разрешение” (Е) использовать в качестве информационного входа демультиплексора, а входы 1, 2, 4 … — в качестве адресных входов демультиплексора А0, А1, А2, … Действительно, при активном значении сигнала на входе Е избирается выход, соответствующий коду, поданному на адресные входы. Поэтому ИС дешифраторов, имеющих разрешающий вход, иногда называют не просто дешифраторами, а дешифраторами-демультиплексорами (например, К155ИД4, К531ИД7 и др.).
1.3 Применение мультиплексоров и демультиплексоров
1.3.1. Термином “мультиплексирование” называют процесс передачи данных от нескольких источников по общему каналу, а устройство, осуществляющее на передающей стороне операцию сведения данных в один канал, принято называть мультиплексором. Подобное устройство способно осуществлять временное разделение сигналов, поступающих от нескольких источников, и передавать их в канал (линию) связи друг за другом в соответствии со сменой кодов на своих адресных входах.
На приемной стороне обычно требуется выполнить обратную операцию – демультиплексирование, т. е. распределение порций данных, поступивших по каналу связи в последовательные моменты времени, по своим приемникам. Эту операцию выполняет демультиплексор. Совместное использование мультиплексора и демультиплексора для передачи данных от n источников к n приемникам по общей линии иллюстрирует рис. 5. (В общем случае число источников данных не равно числу приемников).
1.3.2. Если в схеме (рис. 5) n различных источников и приемников заменить n-разрядными источником и приемником, например, регистрами RGист. и RGпр. (изображены пунктирными линиями), то схема может быть использована для преобразования n-разрядного параллельного кода на передающей стороне в последовательный код (с помощью мультиплексора) и последовательного кода в параллельный на приемной стороне (с помощью демультиплексора). При подобном применении мультиплексора и демультиплексора в качестве их адресных кодов используются выходные сигналы двоичного счетчика, последовательно формирующего на своих выходах двоичные коды чисел от 0 до n-1.
1.3.3. Мультиплексор можно использовать в качестве универсального логического элемента для реализации любой логической функции от числа аргументов, равного числу адресных входов мультиплексора. Покажем это на примере логической функции, заданной своей таблицей истинности (табл. 3).
Выбираем мультиплексор, имеющий три адресных (по числу аргументов функции) и восемь информационных входов. Для реализации заданной функции информационные входы мультиплексора соединим с уровнями логических “1” и “0” в такой последовательности, которая полностью копирует последовательность единиц и нулей функции в таблице истинности (рис. 6). При этом не требуется ни записи СДНФ, ни ее минимизации. Кстати, функция, заданная табл. 3 (четность числа единиц в трехразрядном слове), не упрощается, поэтому для своей реализации, например, в базисе ЛЭ “И-НЕ” требует четырех ЛЭ “3И-НЕ” и трех инверторов, т. е. в сумме потребуется три ИС. В то же время для реализации схемы по рис. 6 требуется всего одна ИС мультиплексора “8-1”. По этой причине, способ реализации функций трех или большего числа аргументов с помощью ИС мультиплексоров весьма популярен у разработчиков.
2. Задание на лабораторную работу
2.1. Используя ЛЭ, установленные на лабораторном стенде, спроектировать схему мультиплексора и исследовать его работу (снять таблицу истинности). Размерность мультиплексора и тип (базис) ЛЭ задаются табл. 4.
Видео:Шифраторы, дешифраторы. Назначение, принцип работы, типовые схемы.Скачать
Уравнение мультиплексора
Дата добавления: 2014-11-27 ; просмотров: 2715 ; Нарушение авторских прав
Простейший мультиплексор 2–1 применяется довольно часто. Как было показано, его работа описывается уравнением
,
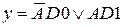
где D0, D1 информационные входы, A – вход управления.
Функционирование мультиплексора, представленного на рис. 3.3,а, описывается уравнением
связывающим сигнал на выходе Y с входными информационными D0,…,D3 и управляющими А, В сигналами.
Для мультиплексора рис. 3.3,б уравнение будет таким
Как видно из этого уравнения, при E = 0 значение выходного сигнала Y будет равно 0, независимо от значений входных и управляющих сигналов.
В интегральном исполнении число информационных входов у мультиплексоров обычно 2, 4, 8 или 16.
На рис. 3.4 представлен мультиплексор 8-1 с инверсным входом разрешения G’, прямым Y и инверсным W выходами (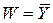 
).
Функционирование мультиплексора, представленного на рис. 3.4, описывается уравнением
Рис. 3.3. Схемы мультиплексоров 4-1:
а) без входа разрешения; б) с входом разрешения Е
 |
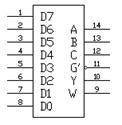Рис. 3.4. Мультиплексор 8-1
| | | следующая лекция ==> | |
| Мультиплексоры | | | Наращивание информационной емкости мультиплексоров |
Не нашли то, что искали? Google вам в помощь!
Видео:Лекция 91. МультиплексорСкачать
Цифровые схемы — мультиплексоры
Мультиплексор — это комбинационная схема, которая имеет максимум 2 n входов данных, n линий выбора и одну выходную линию. Один из этих входов данных будет подключен к выходу на основе значений линий выбора.
Так как есть n строк выбора, будет 2 n возможных комбинаций нулей и единиц. Итак, каждая комбинация выберет только один ввод данных. Мультиплексор также называется Mux .
Видео:Мультиплексоры, принцип действияСкачать
4×1 Мультиплексор
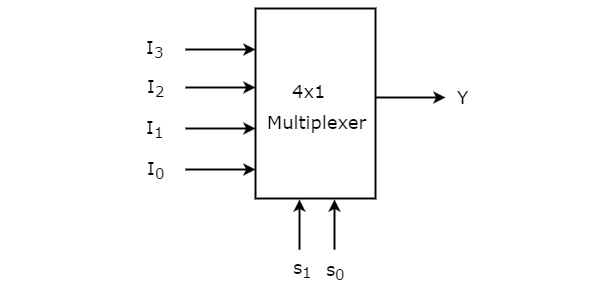
Мультиплексор 4×1 имеет четыре входа данных I 3 , I 2 , I 1 и I 0 , две строки выбора s 1 & s 0 и один выход Y. Блок-схема мультиплексора 4×1 показана на следующем рисунке.
Один из этих 4 входов будет подключен к выходу на основе комбинации входов, присутствующих в этих двух линиях выбора. Таблица истинности мультиплексора 4×1 показана ниже.
| Линии выбора | Выход | |
|---|---|---|
| S 1 | S 0 | Y |
| 0 | 0 | Я 0 |
| 0 | 1 | Я 1 |
| 1 | 0 | Я 2 |
| 1 | 1 | Я 3 |
Из таблицы Truth мы можем напрямую написать булеву функцию для вывода, Y как
Y = S 1 ′ S 0 ′ I 0 + S 1 ′ S 0 I 1 + S 1 S 0 ′ I 2 + S 1 S 0 I 3
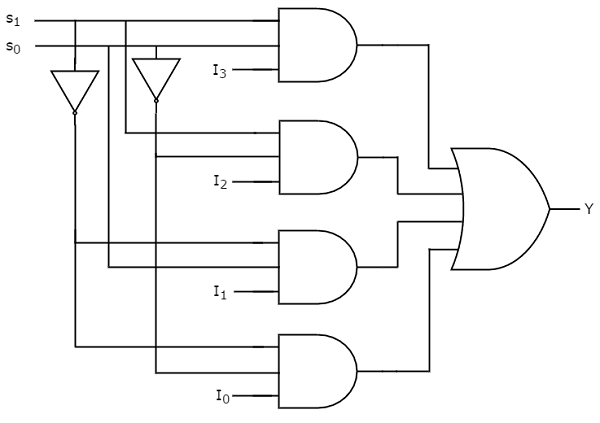
Мы можем реализовать эту булеву функцию с помощью инверторов, вентилей AND и вентиля OR. Принципиальная схема мультиплексора 4×1 показана на следующем рисунке.
Мы можем легко понять работу вышеупомянутой схемы. Аналогично, вы можете реализовать мультиплексор 8×1 и мультиплексор 16×1, следуя той же процедуре.
Видео:4 3 2 Мультиплексоры и демультиплексорыСкачать
Реализация мультиплексоров высшего порядка.
Теперь давайте реализуем следующие два мультиплексора высшего порядка, используя мультиплексоры низкого порядка.
- 8×1 мультиплексор
- 16×1 мультиплексор
8×1 мультиплексор
В этом разделе мы реализуем мультиплексор 8×1, используя мультиплексоры 4×1 и мультиплексор 2×1. Мы знаем, что 4×1 Multiplexer имеет 4 входа данных, 2 строки выбора и один выход. Принимая во внимание, что мультиплексор 8×1 имеет 8 входов данных, 3 строки выбора и один выход.
Итак, нам требуется два мультиплексора 4×1 на первом этапе, чтобы получить 8 входных данных. Поскольку каждый мультиплексор 4×1 производит один выходной сигнал, нам требуется мультиплексор 2×1 на втором этапе, рассматривая выходы первого этапа в качестве входных данных и для получения конечного выхода.
Пусть мультиплексор 8×1 имеет восемь входов данных от I 7 до I 0 , три строки выбора s 2 , s 1 & s0 и один выход Y. Таблица истинности мультиплексора 8×1 показана ниже.
| Выбор входов | Выход | ||
|---|---|---|---|
| S 2 | S 1 | S 0 | Y |
| 0 | 0 | 0 | Я 0 |
| 0 | 0 | 1 | Я 1 |
| 0 | 1 | 0 | Я 2 |
| 0 | 1 | 1 | Я 3 |
| 1 | 0 | 0 | Я 4 |
| 1 | 0 | 1 | Я 5 |
| 1 | 1 | 0 | Я 6 |
| 1 | 1 | 1 | Я 7 |
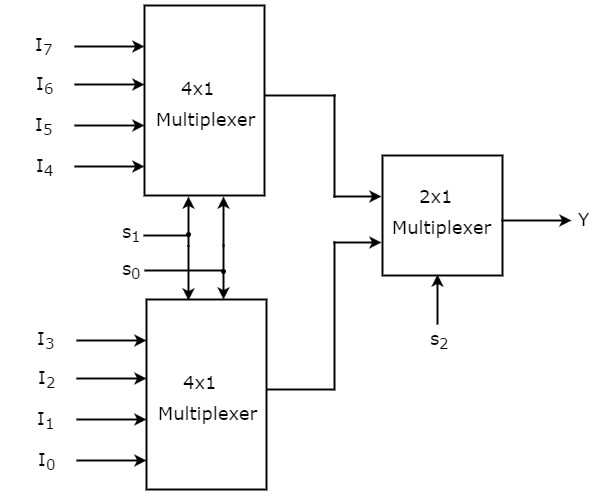
Мы можем легко реализовать мультиплексор 8×1, используя мультиплексоры низкого порядка, рассмотрев приведенную выше таблицу истинности. Блок-схема мультиплексора 8×1 показана на следующем рисунке.
Те же строки выбора, s 1 и s 0 , применяются к обоим мультиплексорам 4×1. Входы данных верхнего мультиплексора 4×1 — от I 7 до I 4, а входы данных нижнего мультиплексора 4×1 — от I 3 до I 0 . Таким образом, каждый мультиплексор 4×1 создает выходной сигнал на основе значений строк выбора, s 1 и s 0 .
Выходы мультиплексоров 4×1 первой ступени применяются в качестве входов мультиплексора 2×1, который присутствует на второй ступени. Другая строка выбора s 2 применяется к мультиплексору 2×1.
Если s 2 равно нулю, то выход мультиплексора 2×1 будет одним из 4 входов от I 3 до I 0 на основе значений линий выбора s 1 & s 0 .
Если s 2 равно единице, то выход мультиплексора 2×1 будет одним из 4 входов от I 7 до I 4 на основе значений линий выбора s 1 & s 0 .
Если s 2 равно нулю, то выход мультиплексора 2×1 будет одним из 4 входов от I 3 до I 0 на основе значений линий выбора s 1 & s 0 .
Если s 2 равно единице, то выход мультиплексора 2×1 будет одним из 4 входов от I 7 до I 4 на основе значений линий выбора s 1 & s 0 .
Таким образом, общая комбинация двух мультиплексоров 4×1 и одного мультиплексора 2×1 работает как один мультиплексор 8×1.
16×1 мультиплексор
В этом разделе мы реализуем мультиплексор 16×1, используя мультиплексоры 8×1 и мультиплексор 2×1. Мы знаем, что мультиплексор 8×1 имеет 8 входов данных, 3 строки выбора и один выход. Принимая во внимание, что мультиплексор 16×1 имеет 16 входов данных, 4 строки выбора и один выход.
Итак, нам требуется два мультиплексора 8×1 на первом этапе, чтобы получить 16 входных данных. Так как каждый мультиплексор 8×1 производит один выход, нам требуется мультиплексор 2×1 на втором этапе, рассматривая выходы первого этапа в качестве входных данных и для получения конечного выхода.
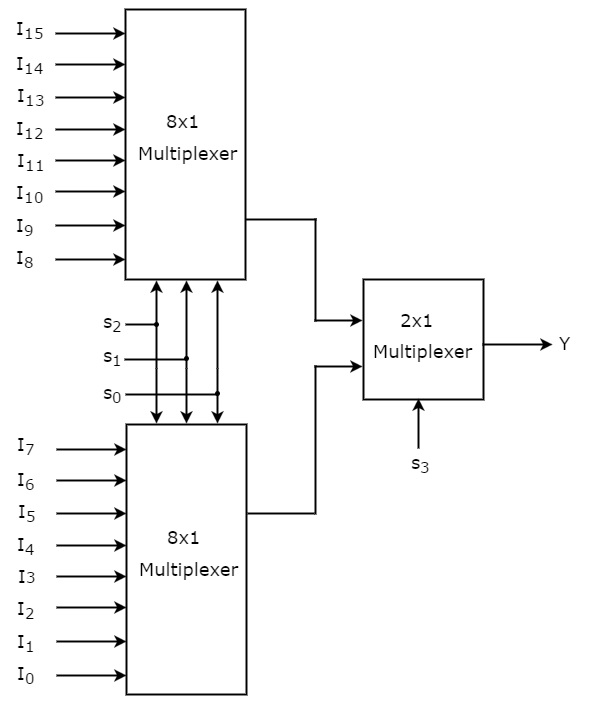
Пусть мультиплексор 16×1 имеет шестнадцать входов данных от I 15 до I 0 , четыре строки выбора от s 3 до s 0 и один выход Y. Таблица истинности мультиплексора 16×1 показана ниже.
| Выбор входов | Выход | |||
|---|---|---|---|---|
| S 3 | S 2 | S 1 | S 0 | Y |
| 0 | 0 | 0 | 0 | Я 0 |
| 0 | 0 | 0 | 1 | Я 1 |
| 0 | 0 | 1 | 0 | Я 2 |
| 0 | 0 | 1 | 1 | Я 3 |
| 0 | 1 | 0 | 0 | Я 4 |
| 0 | 1 | 0 | 1 | Я 5 |
| 0 | 1 | 1 | 0 | Я 6 |
| 0 | 1 | 1 | 1 | Я 7 |
| 1 | 0 | 0 | 0 | Мне 8 |
| 1 | 0 | 0 | 1 | Мне 9 |
| 1 | 0 | 1 | 0 | Мне 10 |
| 1 | 0 | 1 | 1 | Мне 11 |
| 1 | 1 | 0 | 0 | Мне 12 |
| 1 | 1 | 0 | 1 | Мне 13 |
| 1 | 1 | 1 | 0 | Мне 14 |
| 1 | 1 | 1 | 1 | Мне 15 |
Мы можем легко реализовать мультиплексор 16×1, используя мультиплексоры низкого порядка, рассмотрев приведенную выше таблицу истинности. Блок-схема мультиплексора 16×1 показана на следующем рисунке.
Те же строки выбора, s 2 , s 1 и s 0 , применяются к обоим мультиплексорам 8×1. Входы данных верхнего мультиплексора 8×1 — от I 15 до I 8, а входы данных нижнего мультиплексора 8×1 — от I 7 до I 0 . Следовательно, каждый мультиплексор 8×1 создает выходной сигнал на основе значений строк выбора, s 2 , s 1 & s 0 .
Выходы мультиплексоров 8×1 первой ступени применяются в качестве входов мультиплексора 2×1, который присутствует на второй ступени. Другая строка выбора s 3 применяется к мультиплексору 2×1.
Если s 3 равно нулю, то выход мультиплексора 2×1 будет одним из 8 входов от 7 до I 0 на основе значений линий выбора s 2 , s 1 & s 0 .
Если s 3 равен единице, то выход мультиплексора 2×1 будет одним из 8 входов от I 15 до I 8 на основании значений линий выбора s 2 , s 1 & s 0 .
Если s 3 равно нулю, то выход мультиплексора 2×1 будет одним из 8 входов от 7 до I 0 на основе значений линий выбора s 2 , s 1 & s 0 .
Если s 3 равен единице, то выход мультиплексора 2×1 будет одним из 8 входов от I 15 до I 8 на основании значений линий выбора s 2 , s 1 & s 0 .
Таким образом, общая комбинация двух мультиплексоров 8×1 и одного мультиплексора 2×1 работает как один мультиплексор 16×1.
🎥 Видео
Логические элементы И, ИЛИ, Исключающее ИЛИ. История, Теория, Применение.Скачать
Логические выражения, таблицы истинности ,структурная логическая схемаСкачать
Лекция 94. Применение мультиплексораСкачать
3 17 МультиплексорыСкачать
РК6. Схемотехника. МультиплексорыСкачать
Лабораторная работа № 3. Мультиплексоры, демультиплексоры и компараторы кодовСкачать
8 класс. Логические элементыСкачать
Что такое мультиплексор и как он работаетСкачать
11 - Мультиплексор и дешифраторСкачать
Построение таблиц истинностиСкачать
Основы цифровой схемотехники. 07. Мультиплексоры и демультиплексорыСкачать
Построение логических схемСкачать
Лекция 88. ДемультиплексорСкачать
Лекция 85. ДешифраторСкачать
4 1 99 заданиеСкачать
Полусумматоры, сумматоры. Назначение, классификация, принцип работы, типовые схемы.Скачать
