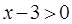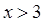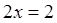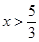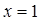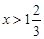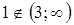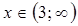Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Логарифмические уравнения и неравенства.
Цель: Закрепить навыки решения логарифмических уравнений и неравенств.
Перед выполнением практической работы необходимо повторить основные методы решения логарифмических уравнений и неравенств.
Учебный элемент № 1
Цель: закрепить решение простейших логарифмических уравнений вида 
Рекомендации к выполнению:
Вспомните определение логарифма.
Повторите схему решения логарифмических уравнений вида
Логарифмическая функция возрастает (или убывает) на промежутке ( 0; + ∞ ) и принимает на этом промежутке все действительные значения. По теореме о корне для любого в данное уравнение имеет единственное решение. Из определения логарифма следует, что а в является таким решением.
Пример: решите уравнение
Решение:
х =1 
Выполните письменную самостоятельную работу (15 мин)

1 . 
2. 
2. 
3. 
3. 
4. 
4. 
5. Lg(2 -5 х ) = 1 (2 б)
Учебный элемент № 2
Цель: закрепить умения решать логарифмические уравнения методом введения новой переменной.
Рекомендации к выполнению:
Внимательно разберите решение примера и выполните задания самостоятельной работы.
Пример. Решите уравнение 

Решение: Введем новую переменную t , t = 
D = (-1) 2 -4∙ 1 (-2) = 9
t 1 = 


Если t = 1 тогда : 
Если t =2, тогда: 

Выполните письменную самостоятельную работу (10 мин)


2. 

2. 

Учебный элемент № 3
Цель: закрепить навыки решения логарифмических уравнений вида 
Рекомендации к выполнению:
Помните, что решение таких уравнений основано на том, что такое уравнение равносильно уравнению f ( x ) = g ( x ) при дополнительных условиях f ( x ) > 0 , g ( x ) > 0.
Можно при решении таких уравнений использовать следующую схему:
f ( x ) = g ( x ) f ( x ) = g ( x )
f ( x ) > 0 или g ( x ) > 0
Внимательно разберите данные ниже решения и выполните задания самостоятельной работы.
Пример: Решите уравнения. 
х 2 — 3х +1 = 2х -3,
Решим уравнение х 2 -3х + 1 = 2х – 3
х 2 – 3х + 1 – 2х + 3 = 0
х 1 = 

x >
Пример: Решите уравнение Lg ( x 2 +75) – Lg ( x -4) =2
Решение: Lg ( x 2 +75) – Lg ( x -4) = 2
Найдем ОДЗ : х 2 +75 > 0
Lg ( x 2 +75)=2 + Lg (х-4)
Lg ( x 2 +75) = Lg 100 + Lg ( x -4)
Lg (x 2 +75) = Lg (100x – 400)
x 2 +75 = 100x – 400
x 2 -100x +75 +400 =0
x 2 -100 x +475 = 0
D = 100 2 – 4 1 475 = 100 000 – 1900 = 8100
x 1 = 
x 2 = 
Выполните самостоятельную работу ( 20 мин).
1. 
1. 
2. Lg (х 2 -17)= Lg (х+3) (3 б)
2.
3. 
3. Lg (х+1) + Lg ( x -1)= Lg 3 2 (4б)
УЧЕБНЫЙ ЭЛЕМЕНТ № 4
Цель : закрепить умения решать простейшие логарифмические неравенства.
Рекомендации к выполнению:
Решение логарифмических неравенств основано на том, что функция у = 
При переходе от простейшего неравенства к равносильным системам неравенств, не содержащих знака логарифма следует учитывать область допустимых значений исходного неравенства.
При решении логарифмических неравенств пользуйтесь следующей схемой:

Видео:Логарифмические уравнения. Практическая часть. 11 класс.Скачать

Урок математики по теме «Решение логарифмических уравнений»
Презентация к уроку
Цели:
- повторить понятия логарифма числа и свойства логарифмов. Ознакомить и закрепить основные методы решения логарифмических уравнений, предупредить появления типичных ошибок.
- Предоставить каждому обучающему возможность проверить свои знания и повысить их уровень.
- Активизировать работу класса через разные формы работы.
- Развивать навыки самоконтроля.
- Воспитывать ответственное отношение к труду, воспитывать волю и настойчивость для достижение конечных результатов.
- создать эмоционально-положительный комфорт (ситуацию успеха)
Задачи урока: Ранее усвоенные знания применять в нестандартных ситуациях.
Знания, умения, навыки и качества, которые актуализируют, закрепят ученики в ходе урока:
- знание понятия логарифма числа, логарифмической функции, свойств логарифмической функции;
- знание основных приёмов решения логарифмических уравнений;
- знание квадратичной функции и её свойств;
- умение выполнять преобразования выражений, содержащих логарифмы;
- умение применять свойства логарифмов при преобразовании выражений, содержащих логарифмы;
- умение решать простейшие логарифмические уравнения и применение основных приёмов при решении более сложных уравнений;
- умение решать квадратные уравнения;
- использовать умение переносить ранее усвоенные знания в новую ситуацию.
Оборудование урока:
- карточки с индивидуальными заданиями для самостоятельной работы;
- карточки с заданиями для домашней работы;
- справочный материал;
- оценочный лист;
- мультимедийный проектор, компьютер.
Формы работы:
- фронтальная;
- работа в парах;
- индивидуальная.
Методы занятия: словесные и практические; контроль и обобщение знаний. При объяснении нового материала: объяснительно-иллюстративный (основное назначение – организация усвоения знаний);частично-поисковый (овладение элементарными навыками поиска знаний, учащиеся привлекаются к самостоятельному решению части проблемы).
План урока:
- Орг.момент.
- Устная работа (морской бой). Найди ошибки. Повторить основные формулы логарифмов.
- Программируемый контроль.
- Из истории математики.
- Изучение нового материала: «Логарифмические уравнения».
- Практическая работа: «Решение логарифмических уравнений».
- Решение проблемной ситуации (если возникнет).
- Итог урока.
- Рефлексия («Что знают», «Чего не знают», «Что получилось?», «Что нет?», «Что необходимо для этого повторить или выучить дома?»).
- Домашнее задание.
Видео:Логарифмические уравнения. 11 класс.Скачать

Ход урока
| Этапы урока | Примечание |
























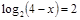 ;
;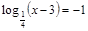 ;
;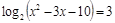 ;
;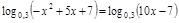 ;
;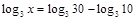 ;
;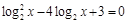 ;
;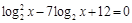 ;
;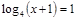 ;
;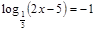 ;
;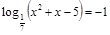 ;
;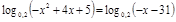 ;
;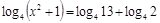 ;
;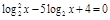 ;
;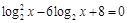 .
.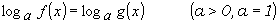 (1)
(1)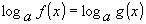 равносильно системе
равносильно системе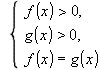 (2)
(2)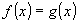 (3)
(3)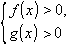 (4),
(4),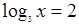 2)
2) 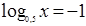 3)
3) 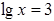
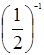 ; x =2 x =1000
; x =2 x =1000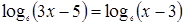 , областью определения логарифмической
, областью определения логарифмической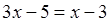 числа, значит,
числа, значит,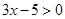 ,
,