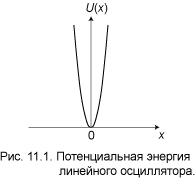
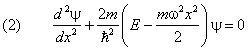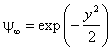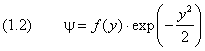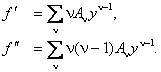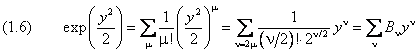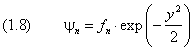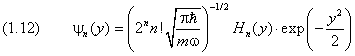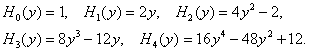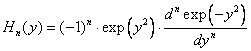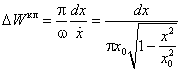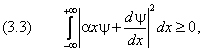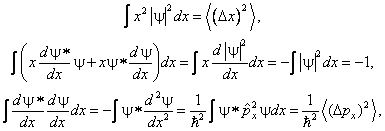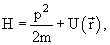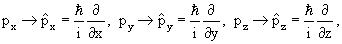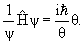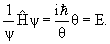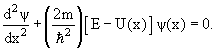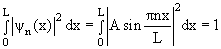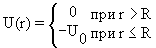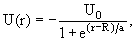Линейным гармоническим осциллятором называется система, потенциальная энергия которой квадратично зависит от координаты:
Здесь m — масса частицы, а ω — собственная частота осциллятора. На рис. 11.1 зависимость (1)
изображена графически. Кривая U ( x ) своей крутизной и бесконечно большой высотой напоминает потенциальную яму. Ниже мы увидим, что линейный осциллятор, действительно, проявляет некоторые свойства частицы в бесконечно высокой потенциальной яме. Например, он имеет бесконечное число дискретных уровней. Но в отличие от отвесных стенок ямы, потенциал осциллятора растёт плавно, и, как следствие, появляется некоторая вероятность обнаружить частицу достаточно далеко от начала координат. Плавная форма потенциала позволяет осциллятору при определённых условиях проявить свойства классической (не квантовой) частицы. Для этого достаточно, чтобы длина волны де Бройля была меньше характерных размеров области изменения потенциала. В случае потенциальной ямы, либо потенциального барьера, такая возможность полностью исключена, так как там потенциал меняется скачком в одной точке. Перейдём к количественному решению задачи.
Напишем одномерное уравнение Шредингера с потенциальной энергией (1):
У него нет естественных граничных условий. Дискретные уровни энергии получаются как следствие ограниченности волновой функции.
Преобразуем уравнение (2): вместо координаты x введём безразмерный аргумент
и вместо E — безразмерную энергию осциллятора
Легко убедиться, что обратная величина подкоренного выражения в (3) равна произведению комптоновской длины волны электрона 
Здесь штрихами обозначено дифференцирование по координате y .
Квантовые свойства осциллятора имеют многочисленные приложения в атомной физике. Ниже мы рассмотрим два из них: влияние нулевых колебаний электромагнитного вакуума на функцию Планка и связанный с ними лэмбовский сдвиг метастабильного уровня атома водорода.
- 11.1 Решение волнового уравнения
- 11.2 Свойства квантового осциллятора
- Линейный гармонический квантовый осциллятор уравнение шредингера и энергетический спектр
- 4.1. Уравнение Шредингера
- Уравнение Шредингера
- 4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
- 4.3. Гармонический осциллятор
- Частица в одномерной потенциальной яме
- 4.4. Частица в поле с центральной симметрией
- 4.5. Орбитальный момент количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Таблица квантовых чисел
- Задачи
- Квантовый гармонический осциллятор
- Конспект лекции (с демонстрациями)
- 🎬 Видео
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

11.1 Решение волнового уравнения
Уравнение (5) решаем методом разложения в ряд с предварительным выделением множителя, быстро убывающего на больших расстояниях от начала координат. Обозначим посредством ψ ∞ волновую функцию при больших значениях аргумента: y ? ε. Ей соответствует асимптотическая форма уравнения Шредингера
Множитель 
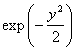
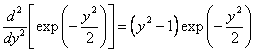
В области больших значений аргумента можно пренебречь единицей по сравнению с y 2 в множителе 
Решение уравнения (5) при произвольных значениях аргумента будем искать в виде
Согласно (5), функция f ( y ) удовлетворяет уравнению
Ищем решение в виде ряда:
Дважды продифференцируем искомую функцию
Подставив эти разложения в (1.3), получим бесконечную цепь линейных уравнений для коэффициентов разложения A ν :
Соберем степени с одинаковыми показателями, для чего индекс первой суммы увеличиваем на два:
Сумма тождественно равна нулю, когда исчезает каждый коэффициент при y ν . Отсюда вытекает рекуррентное соотношение для коэффициентов разложения (1.4):
Задав A0 и A1, мы получим все коэффициенты A n , соответственно, с чётными и с нечётными номерами. Формальное решение задачи получено.
Теперь покажем, что условию ограниченности волновой функции удовлетворяет только конечная сумма, но не бесконечный ряд. Для этого покажем, что ряд, коэффициенты которого подчиняются условию (1.5), растёт быстрее, чем exp ( y 2 /2 ) . Разложим экспоненту в ряд Тейлора:
Здесь ν принимает только чётные значения. Мы ввели обозначение
при больших значениях ν стремится к 1/ ν . В то же время из (1.5) следует:
Теперь ясно, что функция, описываемая соотношением (1.5), растёт быстрее, чем экспонента (1.6). Следовательно, произведение (1.4) при больших значениях аргумента неограниченно возрастает. Поэтому физический смысл имеет только такое решение (1.3), в котором сумма (1.4) содержит лишь конечное число слагаемых.
Покажем, как требование конечности числа слагаемых приводит к дискретному спектру энергетических уровней осциллятора. Пусть n — номер последнего члена ряда (1.4), не равного нулю:
Из (1.5) вытекает связь между величиной энергетического уровня и его номером:
Итак, мы снова получили дискретные уровни энергии. Каждому уровню с номером n соответствует ровно одна волновая функция:
причём нижний предел равен нулю при чётном n и единице — при нечётном. Уровни энергии, согласно (4) и (1.7), принимают дискретный ряд значений:
Обратим внимание на то, что наименьшее из возможных значений энергии, равное
отлично от нуля. Это состояние соответствует так называемым нулевым колебаниям .
Рекуррентное соотношение (1.5) с учётом (1.7) принимает вид
Оно позволяет восстановить все коэффициенты суммы (1.8а) с точностью до общего множителя; последний может быть найден из условия нормировки волновой функции (1.8). Поскольку ν f n является чётной при чётных значениях её номера n , и нечётной — при нечётных n . Она пропорциональна известным в математике полиномам Эрмита H n ( y ). Выпишем для справки нормированную волновую функцию состояния осциллятора с номером n :
Приведём несколько первых полиномов Эрмита:
Исследуем полученное решение.
Видео:Квантовая механика 47 - Стационарное уравнение Шредингера. Гармонический осциллятор.Скачать

11.2 Свойства квантового осциллятора
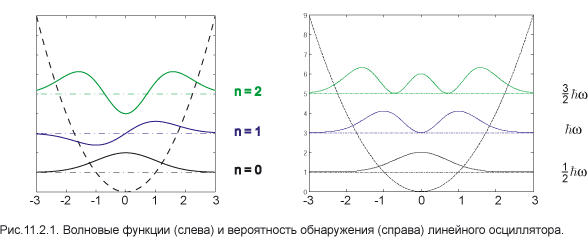
Линейный осциллятор имеет эквидистантную систему уровней: разность энергий двух соседних уровней постоянна и равна ħω. Именно такой квант энергии излучается или поглощается при переходе между соседними уровнями. На рис.11.2.1 слева приведены графики волновой функции для трёх первых значений n . По горизонтальной оси отложены значения безразмерного аргумента y .
Парабола изображает потенциальную функцию, а горизонтальные прямые — значения энергетических уровней. Для удобства восприятия волновые функции сдвинуты по вертикальной оси.
Волновые функции линейного осциллятора и рассмотренной выше задачи о прямоугольной потенциальной яме имеют некоторые сходные черты. Во–первых , у них одинаково количество узлов. Здесь мы ещё раз встречаемся с проявлением осцилляционной теоремы, упомянутой в девятой главе. Так, волновая функция основного состояния ψ0 не обращается в нуль ни в одной точке на прямой, а графики функций ψ1 и ψ2 пересекают горизонтальную ость, соответственно, один и два раза. Для остальных состояний имеет место тот же самый результат. Действительно, из теории специальных функций известно, что полином Эрмита n –го порядка H n имеет ровно n корней. Во–вторых , квантовую частицу можно обнаружить и в области, запрещённой для движения в классической механике, что иллюстрирует график на рис.11.2.1 справа.
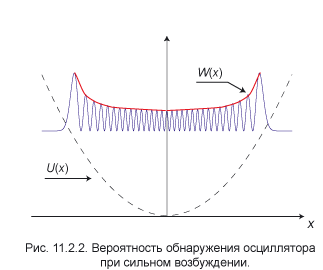
В состояниях с сильным возбуждением квантовый осциллятор приобретает свойства классической частицы. На рис. 11.2.2 схематически изображён график вероятности в
пределе n » 1 . Пунктиром, как и выше, отмечена потенциальная кривая, а синим цветом — вероятность обнаружения. Функция W( x ) быстро осциллирует , причём её огибающая (она обозначена на рисунке красным цветом) монотонно растёт от центра к периферии. Такой рост имеет аналогию в классической механике, когда вероятность обнаружения частицы на отрезке длиной Δ x обратно пропорциональна её скорости V :
В точках поворота скорость обращается в нуль, поэтому там легче всего найти частицу. В самом деле, рассмотрим движение частицы по закону
Классическую вероятность обнаружения частицы на отрезке от x до x + dx определим как отношение времени прохождения отрезка
к половине периода колебаний:
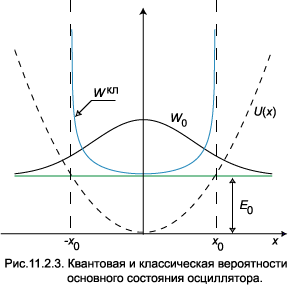
Вероятность значительно увеличивается вблизи точек поворота x = ± x 0 . Для достаточно больших значений n в апертуру прибора с конечной разрешающей способностью попадает много горбов, поэтому осцилляции волновой функции в классическом пределе незаметны. Но для основного состояния квантовая теория и классическая механика дают принципиально разные ответы, что иллюстрирует рис.11.2.3. Зелёная линия на нём
обозначает уровень нулевых колебаний E 0 из (1.10). Классическая вероятность увеличивается по мере приближения к точке x 0, определяемой условием U ( x 0) = E 0, но не может перейти через эту границу. Квантовая теория предсказывает уменьшение вероятности при приближении к границе, причём частица может быть обнаружена в классически недоступной области x > x 0.
11.3. Нулевые колебания
В самом низком состоянии осциллятор имеет отличную от нуля энергию (1.10), определяемую его собственной частотой. Нулевые колебания осциллятора имеют чисто квантовую природу и находят своё объяснение в соотношении неопределённостей. Полная энергия осциллятора равна сумме кинетической и потенциальной

Если частица локализована внутри области размером x , то, согласно принципу Гайзенберга , её импульс не может быть меньше, чем

Таким образом, первое слагаемое в (3.1) уменьшается по мере увеличения x , а второе — растёт:

Полная энергия как функция x имеет минимум в точке


Полученное значение в два раза отличается от результата точного расчёта. Это не удивительно, так как соотношение неопределёностей даёт оценки лишь по порядку величины. Точное выражение для энергии нулевых колебаний получается из упомянутого в главе неравенства для дисперсий момента и координаты:

Формально она выводится следующим образом. Пусть состояние частицы описывается функцией y ( x ), причём средние значения импульса и координаты для простоты вывода предполагаются равными нулю. Напишем очевидное неравенство
где a — действительная постоянная. Далее вычислим три полезных выражения:
Они позволяют преобразовать левую часть (3.3) в квадратичный по a трёхчлен:

Этот трёхчлен не меняет знака ни при каких значениях a , если его дискриминант отрицателен, либо равен нулю. Отсюда вытекает условие
Видео:Микролекция: Гармонический осцилляторСкачать

Линейный гармонический квантовый осциллятор уравнение шредингера и энергетический спектр
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
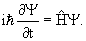 | (4.1) |
где 
в которой 







х → 


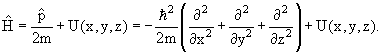 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


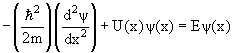
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
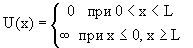 | (4.5) |
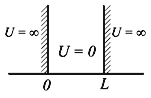
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
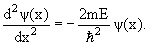 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
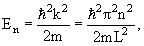 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
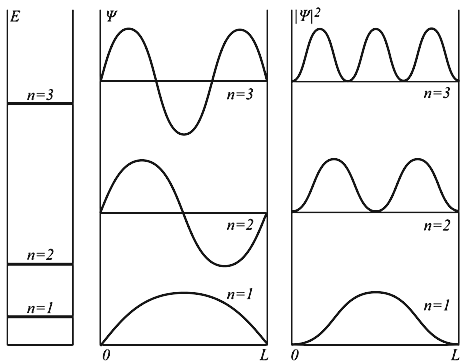
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
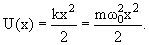 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
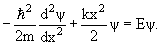 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
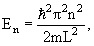

Одномерный гармонический осциллятор:
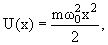
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
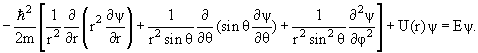 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
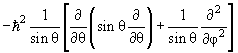 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 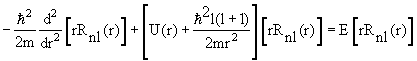 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
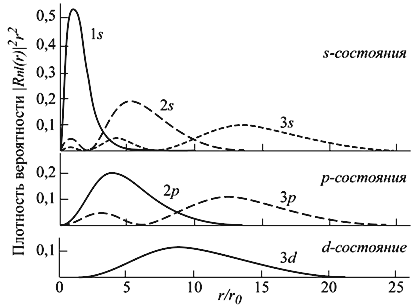
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
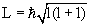 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
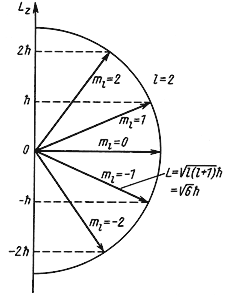
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
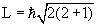
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Видео:Авакянц Л. П. - Введение в квантовую физику - Гармонический осцилляторСкачать

Квантовый гармонический осциллятор
Конспект лекции (с демонстрациями)
Аннотация: изучение качественной стороны решения уравнения Шредингера для гармонического осциллятора, выяснение отличий получаемых результатов от выводов классической механики. (Традиционное изложение темы, дополненное демонстрациями на компьютерных моделях.)
Одна из важных задач о движении микрочастиц – это задача о движении гармонического осциллятора — системе, способной совершать гармонические колебания. 
Рассмотрим одномерный случай. (Трехмерные задачи сложны в математическом отношении, а практически все принципиальные особенности движения микрочастиц можно выявить и на одномерных задачах.) Изменение потенциальной энергии по оси x описывается формулой
Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?
- Колебания маятника с малой амплитудой.
- Другой пример – вертикальные колебания грузика, подвешенного на пружине.
В мире микрочастиц примерами могут быть колебания двухатомной молекулы или колебания атомов в кристаллах. Существенным для всех примеров является ограничение движения некоторой областью значений x. Частица не может покинуть параболическую потенциальную яму, края которой уходят на бесконечность.
Из классической механики известно, что проекция движения частицы на ось x представляет собой синусоидальное колебание около положения равновесия x = 0 с частотой:
Точки a0 и -a0, в которых полная энергия частицы E равна потенциальной энергии, являются для частицы точками поворота. Плотность вероятности обнаружения колеблющейся частицы в различных точках оси x описывается формулой
Минимальна вероятность найти частицу около положения равновесия, где она движется с максимальной скоростью. Вблизи точек поворота частица как бы «зависает», и там вероятность обнаружения максимальна.
Оценка минимальной энергии осциллятора
Посмотрим, к каким выводам о характере движения приводит квантовая механика. Начнем с простой оценки минимального значения энергии осциллятора E. Полная энергия осциллятора E складывается из кинетической и потенциальной энергий:
Используя соотношение неопределенности Гейзенберга, в качестве оценки значения импульса p возьмем p
Для малых значений x кинетическая энергия превышает потенциальную, тогда как при больших значениях x имеет место обратное соотношение между ними. Для основного состояния, где энергия минимальна, найдем минимум функции (2). Значение переменной xmin, соответствующее минимуму, равно:
а соответствующее значение энергии E имеет порядок
Заметим, что оценка энергии основного состояния дает ненулевое(!) значение. Уже простые вычисления приводят к нетривиальному результату.
Решения уравнения Шредингера
Нахождение точного решения требует решения уравнения Шредингера с потенциальной энергией (1), которое имеет вид
Трудности решения связаны со слагаемым, содержащим x 2 . Приведем здесь только результаты вычислений. Анализ показывает, что, как и в случае с прямоугольной потенциальной ямой, волновые функции, являющиеся решением этого уравнения, будут непрерывными и конечными не при всех значениях энергии E, а лишь при дискретном наборе значений:
где n принимает значения 0, 1, 2, . . Отметим, что энергетические уровни гармонического осциллятора в отличие от случая прямоугольной потенциальной ямы расположены на одинаковом энергетическом расстоянии друг от друга ΔE = hυ.
Важной особенностью решения является наличие так называемых нулевых колебаний — колебаний с энергией, соответствующих значению квантового числа n = 0. Отличие от нуля минимальной энергии осциллятора характерно для всех квантовых систем и является следствием соотношения неопределенностей (см. оценку выше). В реальных квантовых системах, например, кристаллах, эти колебания сохраняются, как показывает опыт, даже при температурах, близких к абсолютному нулю, когда, казалось бы, все тепловое движение должно прекратиться. Опыты по рассеянию света кристаллами при низких температурах это подтверждают. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий (пример ниже) и других молекулярных явлений.
Первые три волновых функции гармонического осциллятора выглядят так:
Здесь введено обозначение x0 2 = h/(4π 2 mυ).
Графики этих волновых функций представлены на рисунке ниже.
Пунктиром показаны границы, между которыми совершала бы колебания классическая частица. Значения a0 отличаются для разных n, так как от n зависит энергия Е (
E 1/2 ). Очевидно, что при малых значениях квантового числа n плотность вероятности нахождения частицы, определяемая квадратом модуля волновой функции ψ0(x) 2 , кардинальным образом отличается от плотности вероятности обнаружения классического осциллятора: в основном состоянии максимальное значение вероятности приходится на центр, модуль волновой функции для всех квантовых чисел n имеет наибольшие значения между классическими точками поворота и экспоненциально убывающие «хвосты» вне этих точек.
Определим для основного состояния, как велика вероятность P обнаружения частицы вне пределов классической области, т.е. вне области -a0 Компьютерная модель
Компьютерная модель поможет Вам в исследовании квантового осциллятора. Ее возможности: после того, как Вы зададите порядковый номер атомов Z, из которых состоит молекула (по умолчанию Z=8), компьютер проведет необходимые расчеты и будет готов показать разрешенные значения энергии, соответствующие им волновые функции и распределения плотности вероятности нахождения частицы по координате. Двигайте указатель вдоль оси энергий (мышкой или клавишами со стрелками) и наблюдайте.
- как плотность уровней зависит от массы атомов;
- как энергия частицы зависит от квантового числа n;
- как вероятность обнаружить частицу зависит от x; убедитесь в том, что амплитуда колебаний частицы увеличивается с ростом ее энергии;
- как вероятность обнаружения частицы вне классической области зависит от квантового числа n. Для этого на нижнем графике установите крестик в начало области интегрирования, нажмите клавишу «Enter» и передвиньте крестик в конечную точку. Компьютер рассчитает площадь под кривой, равную вероятности обнаружить частицу в выбранном Вами диапазоне координат;
Смешение состояний (принцип суперпозиции)
Реальные объекты (атомы в молекуле, кристалле. ) редко находятся в основном состоянии. За счет, например, теплового возбуждения реальны состояния с квантовым числом n > 0. Одно из важнейших положений квантовой механики — принцип суперпозиции. Он гласит: если квантовая частица может находиться в состояниях, описываемых функциями Ψ1, Ψ2, . Ψn, то линейная комбинация (суперпозиция) волновых функций Ψi
где сi — произвольные постоянные, также является волновой функцией, описывающей одно из возможных состояний частицы. Коэффициенты сi изменяются во времени. Принцип неопределенности ΔtΔE>h/2π не позволяет определить зависимость от времени этих коэффициентов для конкретного осциллятора (можно, однако, получить средние значения для большого количества осцилляторов).
Для гармонического осциллятора интересен набор состояний, который минимизирует соотношение неопределенности «координата — импульс», т.е. произведение ΔpΔx=h/2π. Впервые он был построен Шредингером в 1926 г. Волновая функция Ψ(x,t) может быть разложена по волновым функциям стационарных состояний осциллятора
Коэффициенты этого разложения
Вероятность осциллятору находиться в состоянии с квантовым числом n равна
т.е. дается распределением Пуассона. Волновая функция Ψ(x,t) представляет нерасплывающийся волновой пакет. Центр пакета движется по классическому закону, ширина пакета не зависит от времени.
Эти состояния называют когерентными, так как они используются для описания когерентных свойств электромагнитного излучения в квантовой теории поля (R. Glauber, Нобелевская премия 2005 года; текст нобелевской лекции, 269 кб). Можно показать, что свободное электромагнитное поле эквивалентно бесконечному набору независимых гармонических осцилляторов.
Со свойствами когерентных состояния гармонического осциллятора можно познакомиться поближе с помощью компьютерной модели (автор L. Kocbach).
Вычисление средних значений
С помощью волновых функций можно найти среднее значение любой величины (если ее можно в принципе измерить экспериментально). Величина |ψ(x)| 2 dx — вероятность нахождения частицы в интервале dx. В случае многократных наблюдений за частицей |ψ(x)| 2 dx — доля частиц, которые находились в этом интервале, т.е. |ψ(x)| 2 является функцией распределения по координате. С ее помощью найдем, что среднее значение координаты
Аналогичным образом находится среднее значение любой функции координаты, например, для потенциальной энергии имеем
В этих формулах, чтобы вычислить среднее значение, мы умножаем значение функции в точке x на вероятность нахождения частицы около x и суммируем по всем возможным значениям x. В качестве примера найдем эти величины для основного состояния гармонического осциллятора
т.к. под интегралом нечетная функция, и
Среднее значение потенциальной энергии равно половине полной энергии этого состояния.
Правило для вычисления средней кинетической энергии отличается от приведенного, т.к. кинетическая энергия является функцией импульса p, а не координаты x:
Для основного состояния гармонического осциллятора
т.е. мы показали, что для основного состояния гармонического осциллятора средние значения потенциальной энергии и кинетической энергии равны между собой и составляют половину полной энергии осциллятора. Можно показать, что это утверждение будет справедливым и для любого другого состояния квантового гармонического осциллятора. Среднее значение потенциальной энергии увеличивается с ростом n, так как при больших значениях n функция ψ(x) заметно отлична от нуля в тех областях оси х, где потенциал U(x) увеличивается. Обратите на это внимание при экспериментах с компьютерной моделью .
Энергия излучения при переходе из одного состояния в другое равна
Набор равноотстоящих энергетических уровней гармонического осциллятора (3) на первый взгляд означает, что осциллятор может поглощать и испускать излучение с частотой, кратной υ, т.е. kυ , где k — разность квантовых чисел начального и конечного уровней осциллятора. Однако, на самом деле это не так. Точный анализ показывает, что если
где n и m квантовые числа начального и конечного состояний, среднее значение координаты не меняется во времени, и такие переходы запрещены.
Проверим выполнение этого условия для гармонического осциллятора. Пусть n=1, а m=0. Опуская постоянные, для интеграла получим выражение
т.к. под интегралом четная функция. Если положить n=2, m=1,
по той же причине. Переходы между соседними уровнями 0↔1 и 1↔2 являются разрешенными. Рассмотрим теперь переход между состояниями n=0 и m=2. Соответствующий интеграл имеет вид
поскольку функция под интегралом нечетная, а пределы симметричны относительно x=0. Следовательно, переходы 0↔2 запрещены. Особенности испускания и поглощения электромагнитного излучения гармоническим осциллятором таковы, что возможны переходы только между соседними уровнями Δn = ± 1. Это правило отбора для гармонического осциллятора.
Трехмерный гармонический осциллятор
В общем случае потенциальная энергия выражается суммой
Уравнение Шредингера допускает разделение переменных. Если решение искать в виде ψ(x,y,z)=X(x)Y(y)Z(z), получается три дифференциальных уравнения, совпадающих по виду с одномерным. Для изотропного случая (kx =ky =kz = k) значения энергии таковы
где квантовые числа n1, n2 и n3 пробегают значения от 0 до бесконечности. Как и в одномерной задаче, налицо дискретность значений энергии, не равная нулю нулевая энергия. Но в трехмерном случае решение определяется тремя квантовыми числами. И особенность: одно и то же значение энергии могут иметь различные состояния, для которых выполнено условие n1+n2+n3 = const. Такие состояния называют вырожденными.
Взаимодействие двух осцилляторов
Существование нулевой энергии (формула (3) при n = 0) сыграло важную роль для объяснения такого загадочного явления, как межатомное взаимодействие у благородных газов. Так как это взаимодействие проявляется в уравнении состояния Ван-дер-Ваальса для реальных газов
оно названо ван-дер-ваальсовским. Если молекулы (атомы) обладают дипольным моментом, то их притяжение обусловлено взаимодействием диполей (качественно и количественно исследованный факт). Но нейтральные молекулы с симметричным в состоянии покоя распределением заряда могут взаимодействовать только при смещении зарядов, вызывающем появление дипольного момента. Такое смещение возникает при не исчезающих ни при каких условиях нулевых колебаний с энергией hυ/2. Появление дипольного момента у одной молекулы индуцирует дипольный момент в другой. Взаимодействие этих быстро меняющихся моментов и обуславливает притяжение.
В качестве простой модели рассмотрим два линейных осциллятора, расположенных на расстоянии R друг от друга и колеблющихся вдоль соединяющей их прямой. Положительные заряды будем считать неподвижными, x1 и x2 — смещение отрицательных частиц (электронов) от положения равновесия.
В отсутствии второго (или при очень большом R) потенциальная энергия каждого осциллятора может быть рассчитана по формуле (1), а частоту колебаний обозначим через υ0
Энергия взаимодействия двух диполей по закону Кулона равна
Первые два слагаемых описывают отталкивание одноименных зарядов разных диполей, а вторые два — притяжение. Всегда R >> x1 и R >> x2. Поэтому разложим дроби в ряды и, удерживая по три члена разложения, получим
Полная энергия двух взаимодействующих осцилляторов равна (здесь p — импульс электрона)
выражение для полной энергии приводится к виду
представляющему сумму энергий двух независимых осцилляторов с несколько отличающимися частотами
Как мы видели, энергия этих осцилляторов имеет квантованные значения (см. (3) выше) и, следовательно, полная энергия нашей системы будет
а для основного состояния (n1 = 0 и n2 = 0)
Теперь надо учесть, что вторые слагаемые под корнями много меньше первых (связь электрона со своим ядром гораздо сильнее связи осцилляторов). Корни квадратные разложим в степенные ряды и ограничимся тремя членами в разложении. Это даст
Последнее выражение равно удвоенной энергии изолированного осциллятора минус небольшая энергия. Поскольку добавка отрицательна, полная энергия взаимодействующих осцилляторов меньше энергии изолированных, для разрыва связи нужно энергию затратить! И, заметим, энергия связи очень быстро убывает с расстоянием
Не было бы нулевых колебаний (чисто квантового эффекта), не существовало бы и связи молекул в основном состоянии.
Ангармонический осциллятор
Гармонический осциллятор — идеализация. Реальные зависимости U(x) выглядят как на рисунке справа. Парабола (штриховая кривая) является хорошим приближением только для малых колебаний вблизи положения равновесия. Для колебаний большой амплитуды формула (3) непригодна, интервалы между верхними уровнями энергии и нижними не одинаковы. Для верхних уровней энергии En потенциальная яма шире параболы, и поэтому интервалы между этими уровнями меньше интервалов между нижними уровнями.
Подведем итоги:
- энергия основного состояния частицы не равна нулю;
- энергия частицы квантована, и значение ее растет линейно с n;
- вероятность обнаружить частицу меняется от точки к точке;
- в трехмерном случае различным состояниям может соответствовать одно и то же значение энергии (вырождение);
- нулевые колебания объясняют происхождение сил притяжения между атомами инертных газов;
- для ангармонического осциллятора уровни не эквидистантны и правило отбора Δn = ± 1 нарушается;
- если значение квантового числа n устремить к бесконечности, решение переходит в классическое.
Если возникли какие-либо вопросы, напишите мне.
🎬 Видео
Гармонический осциллятор. Груз на пружине. 3 метода решения.Скачать

Квантовые гармонический и ангармонический осцилляторы. Жесткий ротатор.Скачать

Введение в квантовый гармонический осциллятор за 9 минутСкачать

Урок 455. Уравнение ШрёдингераСкачать

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Квантовая гармонияСкачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Спектр излучения водорода (видео 12) | Квантовая физика | ФизикаСкачать
Урок 459. Обзор квантовой теории атома водородаСкачать

Парфёнов К. В. - Квантовая теория. Часть 1 - Гармонический осцилляторСкачать

Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

Квантовая физика для чайников!Скачать

Квантовая механика - 1.4 | Квантовый осциллятор | Заиграев Н. М.Скачать

Собственные функции и собственные значения линейного гармонического осциллятораСкачать

Клёнов Н. В. - Атомная физика - Потенциальная яма и гармонический осциллятор (Лекция 5)Скачать