Линейные уравнения и приводимые к ним уравнения с параметрами

Рассмотрим линейные уравнения с параметром вида: $$p(a)x-q(a)=0,$$ где (p(a)) и (q(a))- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все (x) при всех значениях параметра (a). Приведем наше уравнение к виду: $$p(a)x=q(a),$$ Отсюда единственное решение: (x=frac

) при (p(a)≠0.) Если же (p(a)=0) и (q(a)=0), то решением данного уравнения является любое число. И последний случай, когда (p(a)=0),а (q(a)≠0), то уравнение не имеет решений. Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с (x) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились. Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:

Решить уравнение (ax-5a=7x-3) при всех возможных (a).

Перенесем все одночлены с (x) влево, а оставшиеся члены – вправо. И вынесем (x) за скобку, как общий множитель: $$x(a-7)=5a-3;$$ Первый случай, когда ((a-7)≠0). Тогда мы можем поделить все уравнение на (a-7) и выразить: $$x=frac.$$ Второй случай, когда ((a-7)=0), получим уравнение $$x*0=32,$$ которое не имеет решений. Таким образом, мы нашли решения уравнения для всех значений параметра (а). Например, (x=frac) при (a=0,) (x=frac) при (a=1) и т.д.
Ответ: При (a=7) (x∈∅;)
при (a≠7) (x=frac.)

Найдите все (a), при которых корнем уравнения $$ax+5a-2(3x+2)=-5x+a^2$$ будет любое число.

Раскроем скобки и перенесем все члены, содержащие (x), влево, а остальные – вправо. $$ax-6x+5x=-5a+4+a^2$$ Приведем подобные: $$ax-x=a^2-5a+4$$ И вынесем за скобку (x) и разложим квадратный многочлен на множители: $$x(a-1)=a^2-5a+4$$ $$x(a-1)=(a-1)(a-4)$$ Первый случай: ((a-1)=0),т.е. (a=1) $$x*0=(a-1)(a-4)$$ $$x*0=0.$$ Решением уравнения будет любое число.
Второй случай: ((a-1)≠0), т.е. (a≠1) $$x=frac=a-4.$$ Решением данного уравнения будет одно число (x=a-4).
Ответ: (a=1.)

Из ОДЗ видно, что (5a+x≠0) и (x-5a≠0,) таким образом, (x≠±5a.) Приведем уравнение к общему знаменателю (x^2-25a^2) и умножим на него все уравнение: $$x^2-5ax-x^2-10ax-25a^2=-100a^2$$ $$-15ax=-75a^2$$ $$ax=5a^2.$$

После преобразований получили линейное уравнение.

Первый случай: (a=0.) Получаем уравнение (0*x=0.) Решениями этого уравнения будет любое число, кроме (x=0) (ОДЗ (x≠±5a)).

Ответ: При (a=0) решениями уравнения будут все действительные числа, кроме (x=0.) Если (a≠0,) то решений нет.

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

II. Линейные уравнения с параметрами уравнения приводимые к линейным

Оглавление

II. Линейные уравнения с параметрами уравнения приводимые к линейным. 4

III. Примеры простейших линейных уравнений с параметром. 6

IV. Линейные уравнения с параметром, имеющие стандартный канонический вид 9

V. Уравнения, приводимые к линейным уравнениям с параметром. 111

I. Введение

Уравнения и неравенства с параметрами являются традиционно наиболее трудными задачами курса математики. Чаще всего они встречаются в заданиях повышенной сложности, а также ученики довольно часто сталкиваются с такими заданиями на ОГЭ и ЕГЭ. В прошлом году только 13,4 % девятиклассников смогли выполнить задание 23 части С. На следующий год нам тоже предстоит сдавать ОГЭ, а данная тема вызывает наибольшее затруднение. Именно поэтому мы выбрали эту тему.

Цель

Изучение решения линейных уравнений с параметрами.

Задачи

1.Познакомиться с понятием параметра.

2.Изучить общий принцип и метод решения линейных уравнений с параметрами.

3.Рассмотреть различные виды уравнений с параметрами.

4.Научиться решать уравнения с параметрами.

Актуальность

Тема «Решение и исследование уравнений с параметрами» присутствует в материалах ОГЭ и Единого государственного экзамена. Данная тема является одной из самых трудных в курсе алгебры.. Совершенно очевидно, что к «встрече» с такими задачами надо специально готовиться.

Предмет исследования:линейные уравнения с параметром.

Объект исследования:алгоритм решения линейных уравнений с параметрами.

II. Линейные уравнения с параметрами уравнения приводимые к линейным

Параметр (от греческого “parametron” – отмеривающий) – величина, значения которой служат для различения элементов некоторого множества между собой. С использованием параметров проводятся исследования многих систем и процессов реальной жизни. В частности, в физике в качестве параметров могут выступать температура, время и др. В математике параметры вводятся для обозначения некоторой совокупности объектов. Так, уравнение + = с параметрами а, b и с определяет совокупность всех окружностей; уравнение + = 1 – всех единичных окружностей; уравнение + = – совокупность концентрических окружностей с центром в начале координат. Рассмотрим с точки зрения алгебры, как определяется уравнение с параметром.

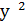
Определение.Уравнение вида Аx=В , где А и В зависят от параметра, то есть А=А(а), В=В(а) называется линейным уравнением с параметром а.

Замечание. Уравнение, которое с помощью тождественных преобразований сводится к уравнению Аx=В, также называется линейным.

Более примитивно линейное уравнение с параметром определяется как уравнение, в запись которого, кроме неизвестных, входят числа, обозначенные буквами.

В отношении уравнений с параметром чаще всего встречаются две постановки задачи:

1) Для каждого значения параметра найти все решения заданного уравнения;

2) Найти все значения параметра, при каждом из которых решения урав- нения удовлетворяют заданным требованиям.

В качестве примера рассмотрим уравнение

1) Пусть , тогда уравнение примет вид

Решим его:

2) Пусть , тогда уравнение примет вид , решением которого является любое действительное значение .

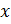
3) Пусть , тогда уравнение примет вид . Решив его, получим, что . В этом случае уравнение не имеет решения.

Следовательно, сам факт существования решения зависит от значения

параметра .

Определение. Исследовать и решить уравнение с параметром это значит :

— найти все системы значений параметров, при которых данное уравнение имеет решение;

— найти все решения для каждой найденной системы значений параметров, т.е. для неизвестного и параметра должны быть указаны свои области допустимых значений.

Видео:Уравнения с параметром. Алгебра 7 класс.Скачать

Подготовка к ЕГЭ №18 Линейные уравнения с параметрами

Решение линейных уравнений с параметрами. Принцип и примеры с решениями.

Просмотр содержимого документа
«Подготовка к ЕГЭ №18 Линейные уравнения с параметрами»

Линейные уравнения и приводимые к ним уравнения с параметрами

Линейным уравнением называется уравнение вида 𝑎𝑥 = 𝑏, где 𝑎, 𝑏 — некоторые действительные числа, x – переменная. В зависимости от коэффициента а, зависит и решение этого уравнения

Если а=0, возникает два вопроса значениях b:

Если а=0, b=0, то уравнение принимает вид 0х=b, значит уравнение имеет бесконечно много решений, решением является любое действительно число.

Если а=0, 𝑏 ≠ 0, то уравнение принимает вид 0х=b, значит уравнение не имеет корней, т.к. нет такого числа, которое при умножении на нуль даст результат, отличный от нуля.

При а≠0 мы можем обе части уравнения разделить на а, имеем единственный корень, равный 𝑥 = 𝑏/а

Ответ: при 𝑎 ≠ 0 единственное решение 𝑥 = 𝑏/ 𝑎 ;

при а=0, b=0 х – любое число;

при а=0, 𝑏 ≠ 0 нет решений;

при 𝑎 ≠ 0 единственное решение 𝑥 = 𝑏 /𝑎 .

Алгоритм решения линейных уравнений с параметром аналитическим способом:

1. Привести уравнение к виду ax = b

2. Найти контрольные значения параметра а.

3. Подставить контрольные значения в уравнение ax = b и выяснить, сколько решений имеет уравнение.

4. Записать, при каких значениях параметра а уравнение имеет единственное решение.

5. Нанести все решения на ось параметров.

6. Записать правильно ответ .

Задача №1. Для каждого значения параметра а решить уравнение 𝑥 − a = 𝑥 + 1

1) Приведем уравнение к виду 𝑎𝑥 = 𝑏, для этого члены, содержащие х, перенесем в левую часть уравнения.

2) Найдем контрольные значения параметра, при которых коэффициент при x обращается в нуль

(𝑎 − 1)(𝑎 + 1) = 0 𝑎 = 1 или 𝑎 = −1

3) Если 𝑎 = 1, то уравнение принимает вид 0 ∙ 𝑥 = 2, т.е. при 𝑎 = 1 уравнение не имеет решений.

4) Если 𝑎 = −1, то уравнение принимает вид 0 ∙ 𝑥 = 0, 𝑥 ∈ Z

5) Если 𝑎 ≠ 1; 𝑎 ≠ −1, то уравнение имеет единственное решение: 𝑥 = ; х= ;

Ответ: при 𝑎 = −1, x – любое; при 𝑎 = 1, решений нет; при 𝑎 ≠ 1; 𝑎 ≠ −1, один корень х= 1/(а−1)

Задача №3. При всех значениях a решите уравнение = 3(𝑥 + 1) +

Решение. Обращаем внимание на то, что параметр находится в знаменателе. А знаменатель дроби не должен быть равен нулю (т.е. параметр имеет область допустимых значений). Контрольными значения параметра, при котором знаменатель дроби равен 0.

1)При a=0 уравнение не имеет корней..

Умножим обе части уравнения на 𝑎 ≠ 0, получим линейное уравнение с параметром.

2ax+2x-3ax-3a=7 2x-ax=7+3a (2-a)x=7+3a

Получим уравнение вида ax=b

контрольные значения параметра: 2-a=0 a=2 Если a=2, то 0∙x=13 уравнение не имеет корней. Если 𝑎 ≠ 2, то уравнение имеет единственное решение 𝑥 = (7+3𝑎) /(2-а)

Ответ: при 𝑎 ≠ 0 и 𝑎 ≠ 2, единственное решение x= (3𝑎+7 ) / (2−𝑎)

при 𝑎 = 0 или 𝑎 = 2, нет корней

Линейные уравнения с параметром при наличии дополнительных условий к корням уравнения.

Задача №4. При каких значениях параметра а уравнение ( − 1) ∙ х = − 2𝑎 − 3 имеет единственное решение, принадлежащее лучу [−1;+∞).

• Найдем контрольные значения параметра, при которых коэффициент при х обращается в нуль:

2) Если а=1, то уравнение принимает вид 0х= -4, т.е. при а=1 уравнение не имеет решений, и условие задачи не выполняется

3) Если а=-1, то уравнение принимает вид 0х=0, 𝑥 ∈ 𝑅. Условие задачи не выполняется.

4) Если а ≠ 1; а ≠ −1 , то уравнение имеет единственное решение: х = −2а−3)/ (−1) х = (а+1)(а−3)/ (а+1)(а−1) х = ( а−3 )/ (а-1 )

Тогда, (а−3) / (а−1) ≥ −1 ( 𝑎−3+𝑎−1) / (𝑎−1) ≥ 0 (2𝑎−4) / (𝑎−1) ≥ 0 (𝑎−2) / (𝑎−1) ≥ 0

Ответ: при 𝑎 ∈ (−∞; −1) ∪ (−1; 1) ∪ [2; +∞ ]

Дробно — рациональные уравнения, сводящиеся к линейным.

Задача №1. Решите уравнение + =

Решение. 1) О.Д.З.: (𝑚 − 1)(𝑥 + 3) ≠ 0 Отсюда 𝑚 ≠ 1; 𝑥 ≠ −3

2) При m=1 , уравнение не имеет корней.

3) При 𝑚 ≠ 1 : Преобразуем исходное уравнение: + = | ∙ (𝑚 − 1)(𝑥 + 3) ≠ 0

3𝑚𝑥 − 5 + (3𝑚 − 11)(𝑥 + 3) = (2𝑥 + 7)(𝑚 − 1)

3𝑚𝑥 − 5 + 3𝑚𝑥 + 9𝑚 − 11𝑥 − 33 = 2𝑥𝑚 − 2𝑥 + 7𝑚 − 7

Получим уравнение вида ax=b (4m-9)𝑥 = 31 − 2m

Контрольные значения параметра: 4𝑚 − 9 = 0 𝑚 =

Если 𝑚 = 2,25 , то 0 ∙ 𝑥 = 31 − 4,5 0 ∙ 𝑥 = 26,5

уравнение не имеет решений.

Если 𝑚 ≠ , то 𝑥 = – единственное решение

4) Учтем О.Д.З.: Найдем значение параметра m, при котором этот корень принимает значение -3

Имеем: = −3 −3(4𝑚 − 9) = 31 − 2𝑚

− 12𝑚 + 27 = 31 − 2𝑚 −10𝑚 = 4 𝑚 = − 0,4

При 𝑚 = − 0,4 уравнение не имеет решений

Ответ: при m = −0,4 ; m = 1; m = 2,25 решений нет;

при m ∈ (−∞; − 2 5 ) ∪ (− 2 5 ; 1) ∪ (1; 9 4 ) 𝑥 = .

Задача №2. При каких значениях параметра а

не имеет решений уравнение − =

Решение. 1) О.Д.З.: 𝑎 ∈ 𝑅, 𝑥 ≠ 2 и 𝑥 ≠ −2

2) На О.Д.З. преобразуем исходное уравнение:

2𝑥 − 𝑎𝑥 + 2𝑥 = 2𝑎 + 1 4𝑥 − 𝑎𝑥 = 2𝑎 + 1

(4 − 𝑎) ∙ 𝑥 = 2𝑎 + 1 Получим уравнение вида ax=b

Контрольные значения параметра: 4 − 𝑎 = 0 𝑎 = 4

Если 𝑎 = 4, то уравнение 0 ∙ 𝑥 = 9 не имеет решений. Если 𝑎 ≠ 4, то 𝑥 = – единственное решение

3) Вернемся к области допустимых значений.

Найдем значения параметра а, при которых этот корень принимает значения 2 и -2.

💡 Видео

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

8 класс, 39 урок, Задачи с параметрамиСкачать

Уравнения с параметрами, приводимые к линейным. Часть 1.Скачать

Уравнения с параметром. Алгебра, 8 классСкачать

10 Линейные уравнения с параметром.Скачать

Линейные уравнения с параметром 7-8 ые классыСкачать

Очень сложное уравнение с модулем. Алгебра 7 класс.Скачать

Линейные уравнения с параметромСкачать

Линейное уравнение с одной переменнойСкачать

#1 ЕГЭ. ПАРАМЕТРЫ С НУЛЯ. Что такое параметры? Линейные уравнения с параметрами.Скачать

Параметры с нуля до уровня ЕГЭ. Линейные уравнения. Математик МГУСкачать

#2 РЕШАЕМ УСЛОЖНЕННЫЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМСкачать

Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать

Линейные уравнения с параметрами. Пример 4. Параметры.Скачать

линейное уравнение с параметромСкачать

Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Линейные уравнения с параметрами. Пример 3. Параметры.Скачать

Линейные уравнения с параметром. Задание №17 в ЕГЭ по математикеСкачать