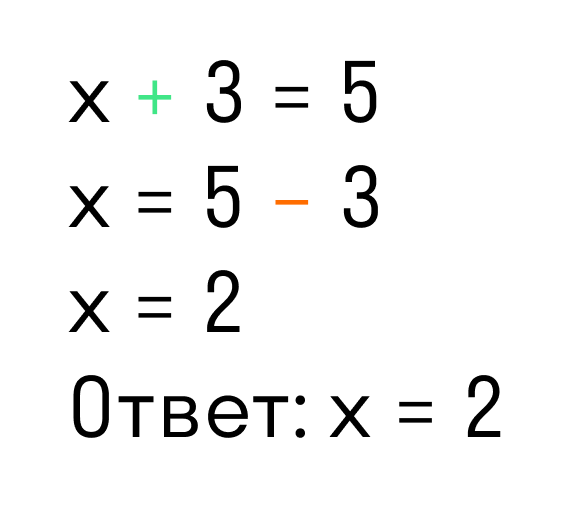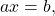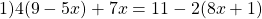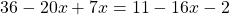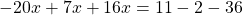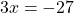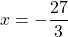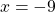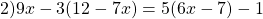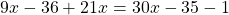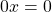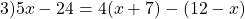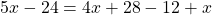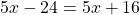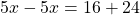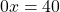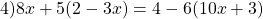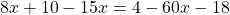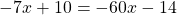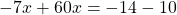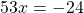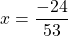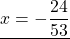Линейные уравнения для 7 класса с решением и ответами

О чем эта статья:

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

если а = 0 — уравнение корней не имеет;

если а и b равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

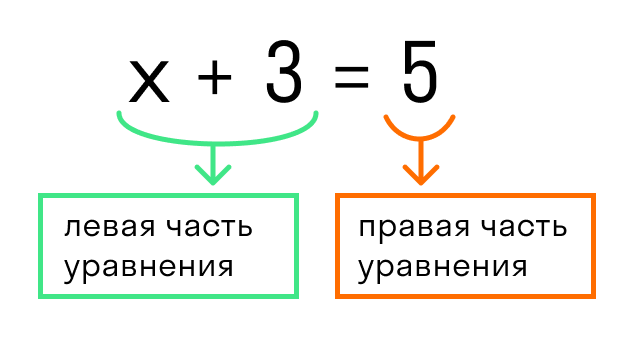
Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

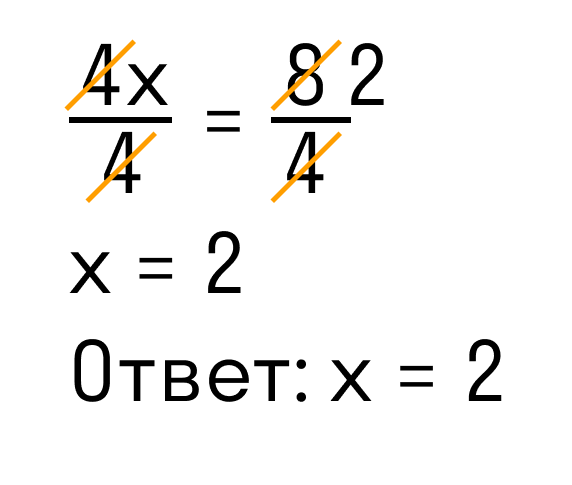
Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

-4x = 12 | : (-4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Видео:Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

Видео:7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Тренировочные упражнения по алгебре на тему: «Линейные уравнения» (7 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Линейные уравнения. Тренировочные упражнения для 7 классов.

Собранный материал содержит тренировочные упражнения, позволяющие научить учащихся 7 классов решать линейные уравнения и уравнения, сводящиеся к линейным. При решении линейных уравнений вида ах=в следует обратить внимание на то, что если а не равно 0, то уравнение ах=в называется уравнением первой степени с одной переменной и имеет один корень, а линейное уравнение может не иметь корней, иметь один корень или бесконечно много. Данные задания могут быть использованы учителем на любом этапе урока в зависимости от целей и задач. Количество времени, отведённое на работу с упражнениями, также зависит от того, на каком этапе они используются, а также от типа школы и контингента учащихся.

№ 1. Решите уравнение:

а) х + 12 = 67; г) 15 — у = 8; ж)14 – х= –11; к) 65+к=54;

б) z + 35 = 87; д) 83 – а = 43; з) у – 33= –8; л) –15+а=22;

в) y – 93 = 18: е) m + 23 = 92; и) х +17= 13; м) 97 –х=100.

№ 2. Найдите корень уравнения:

а) 5х = 60; г) 6у = -18; ж)13у=78; к) –12к= –1,44;

б) 9у = 72; д) -2х = 10; з)1,7с= –0,34; л) 14у= –10;

в) 10 z = 15; е) 11у = 0; и) –7,4х= –1,48; м) 31с=93.

№ 3. Решите уравнение:

а) 4х + х = 70; г) 8х – 7х + 8 =12;

б) 4 · 25 · х = 800; д) у · 5 ·20 = 500;

в) 13у + 15у – 24 = 60; е) 6 z + 5 z – 44 =0.

№ 4. Решите уравнение:

а) 55 : х + 9 =20; г) 48 : (9х – х) =2; ж) 3х+14=35; к) 3=4·(к+2);

б) 88 : х – 24 = 64; д) (у + 6) – 2 = 15; з) 5·(у-9)=-2; л) 5·(с+5)= -7;

в) р · 38 – 76 = 38; е) 2 (а – 5) = 24; и) 3( у–33)=3; м) 2( х – 7)=3.

№ 5. Найдите корень уравнения:

а) (х + 15) – 8 = 17; г) 32 – х = 32 + х; ж) 2х+9=13 –х; к)1,2с+1=1–с;

б) (у – 35) + 12 = 32; д) х – 35 – 64 = 16; з) 14–у=19 –11у; л)3х–8=х+6;

в) 55 – (х – 15) = 30; е) 28 – у +35 = 53; и) 0,5а+11=4–3а; м)х–4х=27.

№ 6. Найдите корень уравнения:

а) 35х = 175; г) 2· (х – 5) =36;

б) m : 35 = 18; д) (у + 25) : 8 =16;

в) ( n -12) · 8 = 56; е) 24 · ( z + 9) = 288.

№ 7. Решите уравнение:

а) 2–3(х+2) = 5–2х; г) 0,4х = 0,4-2(х+2);

б) 0,2 – 2(х+1) = 0,4х; д) 5(2+1,5х)-0,5х=24;

в) 3-5(х+1) = 6-4х; е) 3(0,5х-4)+8,5х=18.

№ 8. Решите уравнение:

а) 4х — 5,5 = 5х — 3(2х-1,5); г) 7·(-3+2х)=-6х-1; ж) 4·(2-3х)=-7х+10;

б) 4 – 5(3х + 2,5) = 3х + 9,5; д) 2·(7+9к)=-6к+2; з) -4·(-к+7)=к+17;

в) 0,4(6х – 7) = 0,5(3х + 7); е) 6·(5-3с)=-8с-7; и) -5·(3а+1)-11=-16.

Видео:Алгебра 7 класс. 11 сентября. Решение линейных уравнений #1Скачать

Линейные уравнения 7 класс

Линейные уравнения, решение которых начинается в курсе алгебры (7 класс) — это уравнения вида

где a и b — числа, x — переменная.

Уравнения, сводящиеся к виду ax=b при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей на число, отличное от нуля (то есть при помощи равносильных преобразований), также часто называют линейными (правильнее называть их уравнениями, сводящимися к линейным).

Рассмотрим примеры уравнений, сводящихся к линейным, которые встречаются в начале курса алгебры 7 класса.

Раскрываем скобки. Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках. Если перед скобками стоит знак «+», знаки не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:

Неизвестные слагаемые переносим в одну сторону, известные — в другую. При переносе знаки слагаемых меняем на противоположные:

Обе части уравнения делим на число, стоящее перед иксом:

Неизвестные слагаемые перенесём в левую часть, известные — в правую. Знак каждого слагаемого при переносе из одной части уравнения в другую меняем на противоположный:

(Обратите внимание: хотя сумма слагаемых с переменной равна нулю, результат записываем не как 0, а как 0x).

Какое бы число мы не подставили в это уравнение вместо x, получим верное равенство.

Ответ: x — любое число.

Можно сначала привести подобные слагаемые, чтобы упростить уравнение:

а уже потом перенести: неизвестные — в одну сторону, известные — в другую:

Это уравнение не имеет корней.

Ответ: нет корней.

Приводим подобные слагаемые:

Переносим неизвестные слагаемые в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

В следующий раз рассмотрим сводящиеся к линейным уравнениям уравнения с дробями.

14 комментариев

А в третьем уравнении ошибку вы допустилтхи. Перенесли неправильно 60х. Ответ должен быть х=24/53.

Спасибо, Маша! Ошибка исправлена.

Мария,всмсле!Там нет ошибок.У меня тоже ответ -24/53.Так как иксы в одну чторону,а числа в другую.Точнее если посмотреть на обычное линейное уравнение, например: x-3=0.
x=0+3
x=3.Обратите внимание,что решая любое уравнение иксы в левой части,а числа в правой (x=3);опять же иксы в левой части,а числа в правой и следовательно мы рассуждаем так во всех уравнениях

я возможно ошибаюсь , но
в уравнении №1) 4(9 — 5x) + 7x = 11 — 2(8x + 1)
ответ будет не -9 , а 9.
т к
3х=-27
х= -27/-3
х=9 , потому что если и в делителе и в знаменателе имеются знаки минуса , оно (как в умножении)становится положительным .

Полли, мы обе части уравнения делим на число, стоящее перед иксом: 3х=-27; х=-27:3, то есть знаки делимого и делителя разные, поэтому ответ со знаком «-«.

Да админ прав, делаем проверку 3X(-9)=-27

Х=-9 Потаму что если в делитиле и в знаментаиле имеются как вы сказали знаки минуса оно как в умножении не меняется.

Нет
Т.к. — делёный на + будет —

Спасибо за понятное изложение темы. Перерыв десяток сайтов и только на вашем нашел ответ на вопрос » как решать линейные уравнения «. Вам + 5 в карму:)

mne tut vse ponjatno. u menja problema s sostavleniem uravnenij/kak zapisatj zada4u matemati4eskim jazikom/ kombinatorika!

🔥 Видео

Уравнения с дробями. Алгебра 7 класс.Скачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Алгебра 7 класс (Урок№43 - Решение линейных уравнений с одним неизвестным.)Скачать

Как решать линейные уравнения Решите уравнение 5 класс 6 класс 7 класс Как решать простое уравнениеСкачать

Линейные уравненияСкачать

№7 Линейное уравнение (5х+4)/2+3=9x/5 Простое уравнение с дробями Решите уравнение с дробью ОГЭ ЕГЭСкачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Решение уравнений, сводящихся к линейным | Алгебра 7 класс #18 | ИнфоурокСкачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

КАК РЕШИТЬ УРАВНЕНИЕ С ДРОБЯМИ, СВОДЯЩЕЕСЯ К ЛИНЕЙНОМУ? Примеры | АЛГЕБРА 7 классСкачать

Алгебра 7 класс (Урок№44 - Решение задач с помощью линейных уравнений.)Скачать

Линейные уравнения с одной переменной . Алгебра . 7 класс .Скачать