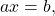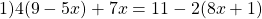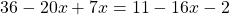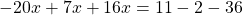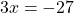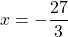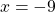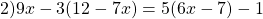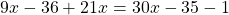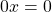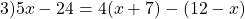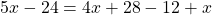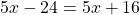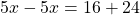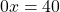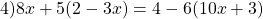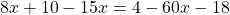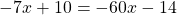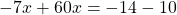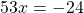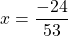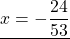О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Понятие уравнения
- Какие бывают виды уравнений
- Как решать простые уравнения
- Примеры линейных уравнений
- Линейные уравнения 7 класс
- 14 комментариев
- Линейное уравнение с одной переменной
- Содержание
- Что такое уравнение
- Приведем пример
- Рассмотрим пример
- Что такое линейное уравнение
- Коэффициенты и решение линейных уравнений
- Свойства линейных уравнений
- 🎦 Видео
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Видео:Алгебра 7 класс с нуля | Математика | УмскулСкачать

Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Видео:7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Линейные уравнения 7 класс
Линейные уравнения, решение которых начинается в курсе алгебры (7 класс) — это уравнения вида
где a и b — числа, x — переменная.
Уравнения, сводящиеся к виду ax=b при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей на число, отличное от нуля (то есть при помощи равносильных преобразований), также часто называют линейными (правильнее называть их уравнениями, сводящимися к линейным).
Рассмотрим примеры уравнений, сводящихся к линейным, которые встречаются в начале курса алгебры 7 класса.
Раскрываем скобки. Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках. Если перед скобками стоит знак «+», знаки не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:
Неизвестные слагаемые переносим в одну сторону, известные — в другую. При переносе знаки слагаемых меняем на противоположные:
Обе части уравнения делим на число, стоящее перед иксом:
Неизвестные слагаемые перенесём в левую часть, известные — в правую. Знак каждого слагаемого при переносе из одной части уравнения в другую меняем на противоположный:
(Обратите внимание: хотя сумма слагаемых с переменной равна нулю, результат записываем не как 0, а как 0x).
Какое бы число мы не подставили в это уравнение вместо x, получим верное равенство.
Ответ: x — любое число.
Можно сначала привести подобные слагаемые, чтобы упростить уравнение:
а уже потом перенести: неизвестные — в одну сторону, известные — в другую:
Это уравнение не имеет корней.
Ответ: нет корней.
Приводим подобные слагаемые:
Переносим неизвестные слагаемые в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
В следующий раз рассмотрим сводящиеся к линейным уравнениям уравнения с дробями.
14 комментариев
А в третьем уравнении ошибку вы допустилтхи. Перенесли неправильно 60х. Ответ должен быть х=24/53.
Спасибо, Маша! Ошибка исправлена.
Мария,всмсле!Там нет ошибок.У меня тоже ответ -24/53.Так как иксы в одну чторону,а числа в другую.Точнее если посмотреть на обычное линейное уравнение, например: x-3=0.
x=0+3
x=3.Обратите внимание,что решая любое уравнение иксы в левой части,а числа в правой (x=3);опять же иксы в левой части,а числа в правой и следовательно мы рассуждаем так во всех уравнениях
я возможно ошибаюсь , но
в уравнении №1) 4(9 — 5x) + 7x = 11 — 2(8x + 1)
ответ будет не -9 , а 9.
т к
3х=-27
х= -27/-3
х=9 , потому что если и в делителе и в знаменателе имеются знаки минуса , оно (как в умножении)становится положительным .
Полли, мы обе части уравнения делим на число, стоящее перед иксом: 3х=-27; х=-27:3, то есть знаки делимого и делителя разные, поэтому ответ со знаком «-«.
Да админ прав, делаем проверку 3X(-9)=-27
Х=-9 Потаму что если в делитиле и в знаментаиле имеются как вы сказали знаки минуса оно как в умножении не меняется.
Нет
Т.к. — делёный на + будет —
Спасибо за понятное изложение темы. Перерыв десяток сайтов и только на вашем нашел ответ на вопрос » как решать линейные уравнения «. Вам + 5 в карму:)
mne tut vse ponjatno. u menja problema s sostavleniem uravnenij/kak zapisatj zada4u matemati4eskim jazikom/ kombinatorika!
Видео:Алгебра 7 класс. 11 сентября. Решение линейных уравнений #1Скачать

Линейное уравнение с одной переменной
Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Содержание
Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Что такое уравнение
Для изучения темы линейного уравнения вспомним, что уравнением называют равенство, в составе которого есть неизвестное число. Это неизвестное число-переменную нам и нужно найти.
К примеру, не будут уравнениями выражения $3n-4$ или $d + 8$. Ведь в них не требуется найти значение переменной и отсутствует знак равенства. Это просто буквенные выражения. А вот записи: $4y-7 = 13$ или $-5x = 6x-2$ являются уравнениями.
Чаще всего уравнения используют, чтобы решить задачу.
Приведем пример
Папе и сыну вместе $45$ лет, при этом известно, что отец старше на $19$ лет. Найдем, сколько лет каждому из них?
Обозначим возраст сына за $x$, тогда папе будет $x+19$ лет. Получим уравнение: $x + (x + 19) = 45$, так как по условию вместе им $45$ лет. Решим:
после раскрытия скобок: $2x + 19 = 45$,
То есть с помощью составления уравнения мы выяснили, что сыну $13$ лет. Отцу тогда $32$ года $(13 + 19)$. И вместе им действительно $45$ лет: $$13 + 32 = 45$$
Таким образом, записав по условию задачи уравнение, мы смоделировали алгебраическую модель ситуации.
Неизвестная переменная может обозначаться в уравнении не только буквами $x$ или $y$, но и любыми другими латинскими буквами.
Когда от нас требуется решить уравнение, мы должны найти все его корни либо показать, что их нет.
Корень уравнения – это значение неизвестной переменной, превращающее уравнение в верное равенство.
Рассмотрим пример
Выясним, является ли корнем этого уравнения $x = 4$. Подставим $4$ вместо $x$ и получим: $$-1 = 5$$$$12-1 = 5$$$$11 = 5$$
При решении мы поняли, что $x ≠ 4$, так как $11 ≠ 5$. То есть число $4$ не может быть корнем данного в задании уравнения. Посчитайте самостоятельно, какой корень у этого уравнения?
Корней может быть несколько, один или не быть совсем. В последнем случае говорят обычно, что уравнение не имеет решения или не имеет корней.
В примере с папой и сыном корень уравнения единственный: $x = 13$. Ведь нет других вариантов решения, при которых будут выполнены все условия и получится верное равенство. Проверьте сами?
Видео:Как решать линейные уравнения Решите уравнение 5 класс 6 класс 7 класс Как решать простое уравнениеСкачать

Что такое линейное уравнение
Если числа в конечном уравнении $2x = 26$ к нашему первому примеру заменить на буквы $a$ и $b$, мы получим уравнение вида $ax = b$.
Подобные уравнения и называются линейными.
Уравнения вида $ax = b$, где $x$ — переменная, $a$ и $b$ — некоторые числа, называются линейными уравнениями с одной переменной
Когда уравнения содержат, к примеру, степень: $$x^2 + 3 = 7$$ или неизвестная переменная находится в знаменателе дроби: $$frac — 3 = 0$$ они не будут называться линейными.
Иногда в составе уравнения есть несколько переменных, это тоже не наш случай: такие уравнения будут изучаться позже.
Видео:ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Коэффициенты и решение линейных уравнений
Числа $a$ и $b$ в линейном уравнении называют коэффициентами. Они могут быть выражены любыми числами, в том числе отрицательными или дробными. При этом $a$ называют коэффициентом при неизвестной переменной, а коэффициент $b$ свободным.
В наших примерах у уравнений был единственный корень. Наверное, вы заметили, что в них коэффициенты $a$ и $b$ были равны числам, отличным от нуля. Подобные уравнения решаются по простому алгоритму: $$x = frac $$
Посмотрим, когда линейное уравнение никак не может иметь корней (или верного решения).
Попробуем взять коэффициент $a$, равный $0$, а коэффициент $b$ — любое число, не равное $0$. Тогда получим уравнение: $$0times x = b$$ При умножении $x$ на ноль всегда будет ноль, но у нас $b ≠ 0$. Следовательно, правая и левая части такого уравнения между собой не равны, и при $a = 0$, а $b ≠ 0$ линейное уравнение не имеет верного решения.
Но линейное уравнение может иметь и множество решений. Рассмотрим такой случай. Например, что будет, если оба коэффициента равны нулю: $a = 0$ и $b = 0$? $$0times x + 0 = 0$$ Ясно, что любое подобное уравнение с обоими коэффициентами, равными нулю, имеет бесконечно много корней. Почему? Потому что любое число при умножении на 0 дает ноль. Какое бы число вместо $x$ мы не подставили, равенство будет верным.
Таким образом, при решении линейных уравнений мы пришли к трем общим ситуациям:
| Величины $a$ и $b$ | $a ≠ 0$, $b$ — любое | $a = b = 0$ | $a = 0$, $b ≠ 0$ |
| Корни уравнения $ax = b$ | $x = frac $ | $x$ — любое | корней нет |
Видео:ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Свойства линейных уравнений
Цель любого линейного уравнения – выразить $x$ и понять, чему он будет равен.
До того, как начать решать уравнение, над ним необходимо произвести все доступные арифметические действия, например, сложение/вычитание, раскрытие скобок, умножение/деление отдельно для свободных коэффициентов и отдельно для членов уравнения с неизвестной переменной.
Для упрощения дальнейшего решения с уравнениями можно произвести те же действия, что применяются к другим математическим выражениям.
Свойства линейных уравнений:
- Любой член можно перенести из одной части линейного уравнения в другую, но при этом нужно не забыть заменить знак на противоположный.
В процессе решения надо так преобразовать уравнение, чтобы все известные члены оказались с одной стороны равенства, а неизвестные — с другой.
Например: $5x = 30-3x$. Для решения перенесем $-3x$ в левую часть с противоположным знаком и получим $5x + 3x = 30$.
- В ходе решения обе части уравнения можно одновременно делить или умножать на какое-то одно и то же число, отличающееся от $0$. При этом равенство будет оставаться верным.
Часто второе свойство применяется в уравнениях с дробями. Например, нужно решить уравнение: $$frac times x = 8$$ Чтобы избавиться от дроби, попробуем и правую и левую части уравнения умножить на $2$. Тогда мы получим: $$2times frac times x = 2times 8$$ После умножения уравнение примет следующий вид: $$5x = 16$$
Согласитесь, такое уравнение решить намного легче. При этом после подобных преобразований равенство не нарушается, и мы получаем равносильные уравнения.
🎦 Видео
ЛИНЕЙНЫЕ УРАВНЕНИЯ с одной переменной. §2 алгебра 7 классСкачать

Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Алгебра 7 класс (Урок№44 - Решение задач с помощью линейных уравнений.)Скачать

7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

Алгебра 7 Линейное уравнение с двумя переменными и его графикСкачать

Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать

Линейные уравнения с одной переменной . Алгебра . 7 класс .Скачать

Уравнения с дробями. Алгебра 7 класс.Скачать

Решение уравнений, сводящихся к линейным | Алгебра 7 класс #18 | ИнфоурокСкачать