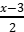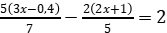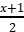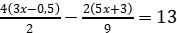Линейные уравнения 10 класс самостоятельная работа (6 видео)

Самостоятельная работа по теме «Линейные уравнения и неравенства» 24 варианта

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

1,2x + 0,8 = 3x – 1 – 1,8x + 1,8

5 – x = 1 – 2x + 4 – 2x

1,2x + 0,8 = 3x – 1 – 1,8x + 1,8

5 – 2x = 1 – x + 4 – x

9x – 15 = 21x – 24

0,6x + 4 + 2x = 4 + 1,6x

1,5x – 3 > 0,2x + 10

27x – 3 = 25 + 27x

12 — 5x + 4 = — 5x + 16

13x + 0,5 = 2,7 + 13x

5 – 3x + 8 = 13 – 3x

7 – 2x = 3 – x + 4 – x

7x – 15 = 19x – 24

0,7x + 4 + 2x = 4 + 1,7x

1,6x – 3 > 0,3x + 10

25x – 3 = 25 + 25x

15 – 5x + 4 = – 5x + 19

1,2x + 1,8 = 3x – 1 – 1,8x + 2,8

5 + 2x = 1 – 2x + 4 + 4x

0,2x + 0,8 = 2x – 1 – 1,8x + 1,8

6 – 2x = 2 – x + 4 – x

7x – 15 = 19x – 24

2,6x + 4 + x = 4 + 3,6x

1,4x – 3 > 0,1x + 10

17x – 3 = 25 + 17x

10 — 5x + 4 = — 5x + 14

10x + 0,5 = 2,7 + 10x

7 – 3x + 8 = 15 – 3x

3,2x + 0,8 = 5x – 1 – 1,8x + 1,8

7 – 3x = 3 – 2 x + 4 – x

5x – 15 = 17x – 24

1,7x + 4 + x = 4 + 2,7x

1,6x – 2 > 0,3x + 11

15x – 3 = 25 + 15x

15 – 7x + 4 = – 7x + 19

Содержание

Краткое описание документа:
Дистанционное обучение как современный формат преподавания
Математика: теория и методика преподавания в образовательной организации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
Самостоятельная работа «Линейные уравнения с одной переменной» 7 класс
Проверочные работы по алгебре 10 класс
📺 Видео

Краткое описание документа:

Это материал для зачета по теме «Линейные уравнения и неравенства» в 24 однотипных вариантах. Каждый вариант содержит однотипные уравнения, начиная с самых простых и заканчивая уравнениями и неравенствами с модулем. Применять можно с 6 класса (только уравнения), с 8 класса — уравнения и неравенства. С 10 класса уже полностью весь вариант.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 949 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 567 721 материал в базе

Другие материалы

18.07.2017
16260
810

17.07.2017
988
0

17.07.2017
265
0

17.07.2017
650
5

17.07.2017
921
0

17.07.2017
1623
1

17.07.2017
420
0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

18.07.2017 3345
DOCX 92.5 кбайт
37 скачиваний
Рейтинг: 4 из 5
Оцените материал:

Настоящий материал опубликован пользователем Агаджанова Ирина Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 5 лет и 3 месяца
Подписчики: 1
Всего просмотров: 50319
Всего материалов: 16

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.

Время чтения: 2 минуты

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Онлайн-конференция о создании школьных служб примирения

Время чтения: 3 минуты

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Самостоятельная работа «Линейные уравнения с одной переменной» 7 класс

Самостоятельная работа. Вариант 1

Линейные уравнения с одной переменной

№1 Выберите уравнение, не имеющее корней:

а) — 2х =7 б) 0х = 4 в) 0х =0 г) 5х = 0

№2 Укажите корень уравнения 4х = 12

а) 2 б) 3 в) 4 г) 6

№3 Решите уравнение: 5 – х = –13

№4 Найдите корень уравнения: а) 6х + 3,6 = 0

б) 7х – 15 = 4х – 3

№5 Найдите, при каком значении переменной значение выражения 23 – 10х равно –7

№6 Решите уравнения: а) 7х – ( 8 – х ) = 6х + 2

б) 10х – 2 (4х – 1 ) = 19

№7 Найдите корень уравнения:

4,2 – 5 (0,2х – 0,5) = 4 (0,5х + 1)

№8 Найдите, при каком значении переменной значение выражения на 3 больше значения выражения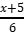

№9 Примените формулы сокращенного умножения и решите уравнение: 2 (х+1) 2 – ( х – 3 )(х + 3) = 7 + х 2

№10 Найдите корень уравнения:

Самостоятельная работа. Вариант 2

Линейные уравнения с одной переменной

№1 Выберите уравнение, не имеющее корней:

а) — 3х =8 б) 0х = 5 в) 3х =0 г) 0х = 0

№2 Укажите корень уравнения 5х = 20

а) 2 б) 3 в) 4 г) 6

№3 Решите уравнение: 6 – х = –11

№4 Найдите корень уравнения: а) 8х + 4,8 = 0

б) 10х – 12 = 7х – 3

№5 Найдите, при каком значении переменной значение выражения 23 – 10х равно –1

№6 Решите уравнения: а) 5х – ( 7 – х ) = 4х – 9

б) 13 – х = 6 ( 9 – х )

№7 Найдите корень уравнения:

2,9 – 5 (0,6х + 0,5) = 2 (0,5х +3)

№8 Найдите, при каком значении переменной значение выражения на 3 меньше значения выражения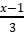

№9 Примените формулы сокращенного умножения и решите уравнение: 2 (х – 2)(х + 2) – (х – 1) 2 = х 2 – 5

№10 Найдите корень уравнения:

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Проверочные работы по алгебре 10 класс

Самостоятельная работа по теме «Решение уравнений и систем уравнений (повторение).»

1); 2); 3)

Самостоятельная работа по теме «Решение уравнений и систем уравнений (повторение)»

1); 2); 3)

Самостоятельная работа по теме «Решение неравенств». Повторение.

1); 2); 3); 4); 5).

Самостоятельная работа по теме «Решение неравенств». Повторение.

1); 2); 3); 4); 5).

Самостоятельная работа по теме «Функция». Повторение.

Дана функция

а) Найдите , , , .

б) Постройте график данной функции.

в) Укажите для данной функции D(y), E(y), промежутки знакопостоянства.

Самостоятельная работа по теме «Функция». Повторение.

Дана функция

а) Найдите , , , .

б) Постройте график данной функции.

в) Укажите для данной функции D(y), E(y), промежутки возрастания и убывания.

Самостоятельная работа по теме «Функция». Повторение.

Дана функция

а) Найдите , , , .

б) Постройте график данной функции.

в) Укажите для данной функции D(y), E(y), промежутки знакопостоянства.

Самостоятельная работа по теме «Функция». Повторение.

Дана функция

а) Найдите , , , .

б) Постройте график данной функции.

в) Укажите для данной функции D(y), E(y), промежутки возрастания и убывания.

Самостоятельная работа по теме «Функция». Повторение.

Дана функция

а) Найдите , , , .

б) Постройте график данной функции.

в) Укажите для данной функции D(y), E(y), промежутки знакопостоянства.

Самостоятельная работа по теме «Функция». Повторение.

Дана функция

а) Найдите , , , .

б) Постройте график данной функции.

в) Укажите для данной функции D(y), E(y), промежутки возрастания и убывания.

Контрольная работа по теме «Повторение материала курса алгебры VII—IX классов»

1. Решите уравнение .

2. Найдите область определения функции .

3. Решить систему уравнений:

4. Решить совокупность неравенств:

Дополнительное задание. Решить систему уравнений:

Контрольная работа по теме «Повторение материала курса алгебры VII—IX классов»

1. Решите уравнение .

2. Найдите область определения функции .

3. Решить систему уравнений:

4. Решить систему неравенств:

Дополнительное задание. Решить систему уравнений:

Контрольная работа по теме «Повторение материала курса алгебры VII—IX классов»

1. Решите уравнение .

2. Найдите область определения функции .

3. Решить систему уравнений:

4. Решить совокупность неравенств:

Дополнительное задание. Решить систему уравнений:

Контрольная работа по теме «Повторение материала курса алгебры VII—IX классов»

1. Решите уравнение .

2. Найдите область определения функции .

3. Решить систему уравнений:

4. Решить систему неравенств:

Дополнительное задание. Решить систему уравнений:

Самостоятельная работа по теме «Показательная функция»

1. Сравнить числа: а) и ; б) и ; в) и .

2. Построить эскиз графиков функций: а); б); в).

3. Построить графики функций: а); б); в).

Самостоятельная работа по теме «Показательная функция»

1. Сравнить числа: а) и ; б) и ; в) и .

2. Построить эскиз графиков функций: а); б); в).

3. Построить графики функций: а); б); в).

Самостоятельная работа по теме «Показательные уравнения»

1); 2); 3) .

Самостоятельная работа по теме «Показательные уравнения»

1); 2); 3) .

Самостоятельная работа по теме «Показательные неравенства»

1) ; 2); 3).

Самостоятельная работа по теме «Показательные неравенства»

1) ; 2); 3).

Контрольная работа по теме «Показательная функция»

1. Построить график функции .

2. Решить уравнения: а), б).

3. Решить неравенства: а); б) .

4. Решить систему уравнений:

Контрольная работа по теме «Показательная функция»

1. Построить график функции .

2. Решить уравнения: а), б).

3. Решить неравенства: а); б) .

4. Решить систему уравнений:

Самостоятельная работа по теме «Понятие логарифма»

1. Вычислите: а); б); в); г).

2. Решить уравнения: а); б).

Самостоятельная работа по теме «Понятие логарифма»

1. Вычислите: а); б); в); г).

2. Решить уравнения: а); б).

Самостоятельная работа по теме «Основные свойства логарифма»

1. Найти , если известно, что .

2. Вычислить: а); б).

Самостоятельная работа по теме «Основные свойства логарифма»

1. Найти , если известно, что .

2. Вычислить: а); б).

Самостоятельная работа по теме «Логарифмическая функция»

Найдите область определения каждой из функций:

1); 2); 3).

Самостоятельная работа по теме «Логарифмическая функция»

Найдите область определения каждой из функций:

1); 2); 3).

Самостоятельная работа по теме «График логарифмической функции»

Построить график функции:

1), 2), 3), 4).

Самостоятельная работа по теме «График логарифмической функции»

Построить график функции:

1), 2), 3), 4).

Самостоятельная работа по теме «Обратная функция»

1),

2), ,

3).

а) Найдите функцию, обратную данной,

б) Укажите область определения и область значений обратной функции,

в) Постройте графики данной функции и обратной в одной системе координат.

Самостоятельная работа по теме «Обратная функция»

1),

2), ,

3).

а) Найдите функцию, обратную данной,

б) Укажите область определения и область значений обратной функции,

в) Постройте графики данной функции и обратной в одной системе координат.

Самостоятельная работа по теме «Обратная функция»

1),

2), ,

3).

а) Найдите функцию, обратную данной,

б) Укажите область определения и область значений обратной функции,

в) Постройте графики данной функции и обратной в одной системе координат.

Самостоятельная работа по теме «Обратная функция»

1),

2), ,

3).

а) Найдите функцию, обратную данной,

б) Укажите область определения и область значений обратной функции,

в) Постройте графики данной функции и обратной в одной системе координат.

Контрольная работа по теме: «Логарифм».

1. Вычислить: а); б) ; в); г); д); е).

2. Найти х, если .

3. Найти область определения функции: .

4. Построить график функции: .

5. Найти функцию, обратную к функции , . Указать область определения и область значений обратной функции.

Контрольная работа по теме: «Логарифм».

1. Вычислить: а); б) ; в); г); д); е).

2. Найти х, если .

3. Найти область определения функции: .

4. Построить график функции: .

5. Найти функцию, обратную к функции , . Указать область определения и область значений обратной функции.

Самостоятельная работа по теме «Логарифмические уравнения»

1), 2), 3), 4).

Самостоятельная работа по теме «Логарифмические уравнения»

1), 2), 3), 4).

Самостоятельная работа по теме «Логарифмические неравенства»

1), 2), 3),

4), 5).

Самостоятельная работа по теме «Логарифмические неравенства»

1) , 2), 3),

4), 5).

Контрольная работа по теме «логарифмические уравнения и неравенства»

1. Решите уравнения: а); б); в).

2. Решить систему уравнений:

3. Решить неравенства: а); б).

4. Решить уравнение: .

Контрольная работа по теме «логарифмические уравнения и неравенства»

1. Решите уравнения: а); б); в).

2. Решить систему уравнений:

3. Решить неравенства: а); б).

4. Решить уравнение: .

Самостоятельная работа по теме «Основы тригонометрии»

1. Выразите в радианной мере величины углов 640; 1600.

2. Выразите в градусной мере величины углов , .

3. Укажите знак числа: а); б).

4. Дано: , . Найдите и .

Самостоятельная работа по теме «Основы тригонометрии»

1. Выразите в радианной мере величины углов 560; 1700.

2. Выразите в градусной мере величины углов , .

3. Укажите знак числа: а); б).

4. Дано: , . Найдите и .

Самостоятельная работа по теме «Основы тригонометрии»

1. Выразите в радианной мере величины углов 720; 1400.

2. Выразите в градусной мере величины углов , .

3. Укажите знак числа: а); б).

4. Найдите и, если известно, что и не лежит во второй четверти.

Самостоятельная работа по теме «Основы тригонометрии»

1. Выразите в радианной мере величины углов 420; 1300.

2. Выразите в градусной мере величины углов , .

3. Укажите знак числа: а); б).

4. Найдите и, если известно, что и не лежит во первой четверти.

Самостоятельная работа по теме «Повторение основных тригонометрических формул»

1. Упростить выражение: .

2. Упростите выражение: .

3. Докажите тождество: .

Самостоятельная работа по теме «Повторение основных тригонометрических формул»

1. Упростить выражение: .

2. Упростите выражение: .

3. Докажите тождество: .

Самостоятельная работа по теме «Повторение основных тригонометрических формул»

1. Упростить выражение: .

2. Упростите выражение: .

3. Докажите тождество: .

Самостоятельная работа по теме «Повторение основных тригонометрических формул»

1. Упростить выражение: .

2. Упростите выражение: .

3. Докажите тождество: .

Самостоятельная работа по теме «Сумма и разность тригонометрических функций»

1. Вычислите: .

2. Докажите тождество: .

3. Преобразуйте в произведение: .

Самостоятельная работа по теме «Сумма и разность тригонометрических функций»

1. Вычислите: .

2. Докажите тождество:.

3. Преобразуйте в произведение:.

Самостоятельная работа по теме «Сумма и разность тригонометрических функций»

1. Вычислите: .

2. Докажите тождество: .

3. Преобразуйте в произведение: .

Самостоятельная работа по теме «Сумма и разность тригонометрических функций»

1. Вычислите:.

2. Докажите тождество:.

3. Преобразуйте в произведение: .

Контрольная работа по теме «Тригонометрические преобразования»

1. Упростите выражение: .

2. Вычислите .

3. Вычислите .

4. Вычислите .

5. Преобразуйте в произведение .

1. Дано: . Найдите и наибольшее значение .

2. Начертите график функции .

Контрольная работа по теме «Тригонометрические преобразования»

1. Упростите выражение: .

2. Упростите выражение: .

3. Вычислить .

4. Вычислите .

5. Преобразовать в произведение .

1. Дано: . Найдите и наименьшее значение .

2. Начертите график функции .

Контрольная работа по теме «Тригонометрические преобразования»

1. Вычислите .

2. Вычислите .

3. Вычислите .

4. Вычислите .

5. Преобразовать в произведение .

1. Дано: . Найдите и наибольшее значение .

2. Начертите график функции .

Контрольная работа по теме «Тригонометрические преобразования»

1. Вычислите .

2. Упростите выражение: .

3. Вычислите .

4. Вычислите .

5. Преобразовать в произведение: .

1. Дано: . Найдите и наименьшее значение .

2. Начертите график функции .

Самостоятельная работа по теме «Уравнение cosx=a»

1), 2), 3)

Самостоятельная работа по теме «Уравнение cosx=a»

1), 2), 3)

Самостоятельная работа по теме «Уравнение cosx=a»

1), 2), 3)

Самостоятельная работа по теме «Уравнение cosx=a»

1), 2), 3)

1); 2); 3).

Самостоятельная работа по теме «Тригонометрические уравнения»

1), 2), 3), 4).

Самостоятельная работа по теме «Тригонометрические уравнения»

1), 2), 3), 4).

Контрольная работа по теме «Тригонометрические уравнения и неравенства»

1. Решите уравнение: а) ; б); в).

2. Решите неравенство: .

3. Решите систему уравнений:

4. Решите неравенство: .

Контрольная работа по теме «Тригонометрические уравнения и неравенства»

1. Решите уравнение: а) ; б); в).

2. Решите неравенство: .

3. Решите систему уравнений:

4. Решите неравенство: .

Контрольная работа по теме «Тригонометрические уравнения и неравенства»

1. Решите уравнение: а) ; б); в).

2. Решите неравенство: .

3. Решите систему уравнений:

4. Решите неравенство: .

Контрольная работа по теме «Тригонометрические уравнения и неравенства»

1. Решите уравнение: а) ; б); в).

2. Решите неравенство: .

3. Решите систему уравнений:

4. Решите неравенство: .

Самостоятельная работа по теме «Четность и нечетность тригонометрических функций»

Исследуйте функции на четность:

1) ; 2); 3); 4).

Самостоятельная работа по теме «Четность и нечетность тригонометрических функций»

Исследуйте функции на четность:

1) ; 2); 3); 4).

Самостоятельная работа по теме «Периодичность тригонометрических функций»

1. Найдите наименьший положительный период функции:

а); б); в); г).

2. — нечетная функция, определена на , периодическая с главным периодом 6. При этом

Постройте ее график на .

Самостоятельная работа по теме «Периодичность тригонометрических функций»

1. Найдите наименьший положительный период функции:

а); б); в); г).

2. — нечетная функция, определена на , периодическая с главным периодом 6. При этом

Постройте ее график на .

Контрольная работа по теме «Тригонометрические функции»

1. Найдите область определения функции .

2. Найдите область значений функции . Укажите, при каких значениях аргумента функция достигает наибольшего и наименьшего значения (если таковые существуют).