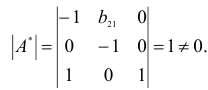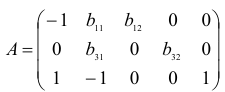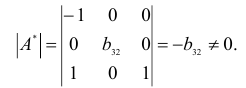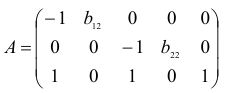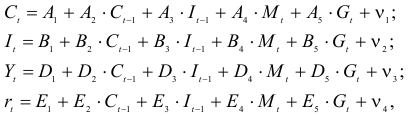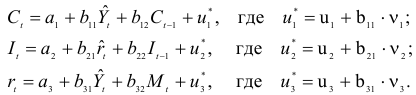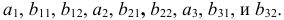Эконометрика как учебная дисциплина на современном этапе благодаря своей универсальности и возможности практического использования для анализа реальных экономических объектов является одним из базовых курсов в системе высшего экономического образования.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
- Эконометрика
- Виды систем эконометрических уравнений
- Проблема идентификации
- Решение эконометрических уравнений
- Пример задачи с уравнением №4.2.1.
- Пример задачи с уравнением №4.2.2.
- Пример задачи с уравнением №4.2.3.
- Пример задачи с уравнением №4.2.4.
- ПРИМЕНЕНИЕ ЭЛЕМЕНТОВ ЛИНЕЙНОЙ АЛГЕБРЫ К РЕШЕНИЮ ЭКОНОМИЧЕСКИХ ЗАДАЧ
- 🔍 Видео
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Эконометрика
Эконометрика — это статистико-математический анализ экономических отношений.
Сущность эконометрики заключается в модельном описании функционирования конкретной экономической системы (экономики данной страны, спроса-предложения в данное время в данном месте и т.д.). Одним из основных этапов эконометрических исследований является анализ устойчивости построенной модели, отражающей взаимосвязи между экономическими показателями, и проверка ее на адекватность реальным экономическим данным и процессам.
Виды систем эконометрических уравнений
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений.
Различают несколько видов систем уравнений, применяемых в эконометрике:
• система независимых уравнений — когда каждая зависимая переменная 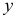
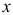
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый к каждому уравнению в отдельности;
• система рекурсивных уравнений — когда зависимая переменная 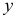
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый последовательно к каждому уравнению в отдельности;
• система взаимосвязанных (совместных) уравнений — когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а другие в правую:
Такая система уравнений называется структурной формой модели. Для построения таких систем и нахождения их параметров используются косвенный и двухшаговый методы наименьших квадратов.
Возможно эта страница вам будет полезна:
Введем следующие определения:
- Эндогенные переменные — взаимозависимые переменные, которые определяются внутри системы (модели)
.
- Экзогенные переменные — независимые переменные, которые определяются вне системы
.
- Лаговые эндогенные переменные — эндогенные переменные за предыдущие моменты времени.
- Предопределенные переменные — экзогенные и лаговые эндогенные переменные системы.
- Коэффициенты
и
при переменных — структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы — приведенная форма модели:
где 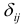
Проблема идентификации
При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация -это единственность соответствия между приведенной и структурной формами модели.
С позиции идентифицируемости структурные модели можно подразделить на три вида:
- идентифицируемые;
- неидентифицируемые;
- сверхидентифицируемые.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
Модель еверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы.
Сверхидентифицируемая модель, в отличие от неидентифицируемой, модели практически решаема, но требует для этого специальных методов исчисления параметров.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой.
Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.
Обозначим через 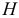
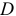
- уравнение идентифицируемо, если
;
- уравнение сверхидентифицируемо, если
;
- уравнение неидентифицируемо, если
.
Если необходимое условие выполнено, то далее проверяется достаточное условие идентификации.
Достаточное условие идентификации — определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифицированных -двухшаговый метод наименьших квадратов.
Косвенный МНК состоит в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым МНК, и находят расчетные значения этих эндогенных переменных по соответствующим уравнениям приведенной системы;
• обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части уравнения.
Решение эконометрических уравнений
Пример задачи с уравнением №4.2.1.
Рассматривается модель протекционизма Сальватора (упрощенная версия):
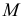
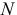
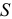
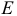
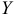
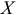
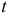
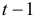
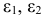
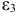
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 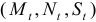
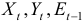
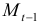
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает три эндогенные переменные 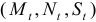
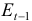
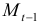
Это уравнение включает три эндогенные переменные 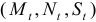
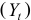
Это уравнение включает три эндогенные переменные 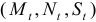
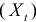
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее, чем число эндогенных переменных модели минус 1, т.е. в данной задаче больше или равен 3-1=2.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
Следовательно, для 1 уравнения достаточное условие выполняется, это уравнение точно идентифицируемо. 2 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
так как она содержит отличный от нуля минор второго порядка
Следовательно, для 2 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо. 3 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы 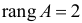
Следовательно, для 3 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо.
- Таким образом, система в целом сверхидентифицируема, для оценки ее параметров можно применить двухшаговый метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
Пример задачи с уравнением №4.2.2.
Рассматривается структурная модель вида:
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
- Исходя из приведенной формы модели уравнений
найти структурные коэффициенты модели.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 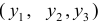
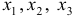
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 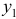
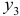
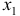
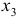
Это уравнение включает три эндогенные переменные 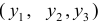
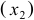
Это уравнение включает две эндогенные переменные (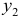
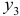
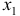
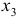
Для этого составим матрицу коэффициентов при переменных модели:
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для первого уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для второго уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для третьего уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
- Все уравнения системы точно идентифицируемы, следовательно, система в целом точно идентифицируема, для оценки ее параметров может быть применен косвенный метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
- Вычисление структурных коэффициентов модели:
1) из третьего уравнения приведенной формы выразим 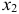
Данное выражение содержит переменные 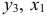
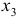
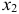
Откуда получим первое уравнение СФМ в виде
2) во втором уравнении СФМ нет переменных 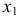

Первый этап: выразим 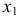
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует 

Подставим его в выражение для
Второй этап: аналогично, чтобы выразить 
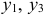
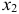

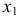
Подставим полученные 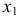

В результате получаем второе уравнение СФМ
3) из второго уравнения ПФМ выразим 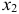
Подставим полученное выражение в третье уравнение ПФМ
В результате получаем третье уравнение СФМ
Таким образом, СФМ примет вид
Пример задачи с уравнением №4.2.3.
Изучается модель вида
где 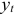
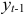
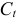
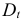
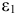
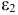
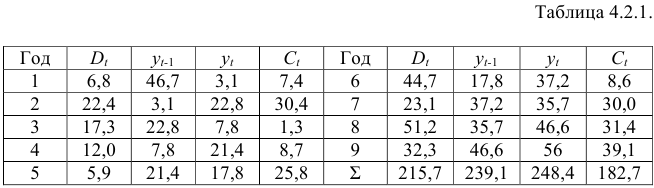
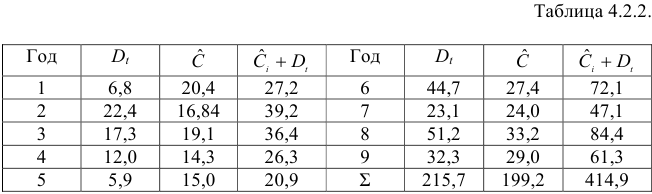
Информация за девять лет о приросте всех показателей дана в таблице 4.2.1.
Для данной модели была получена система приведенных уравнений
- Применив необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое из уравнений модели.
- Рассчитать параметры первого уравнения структурной модели.
Решение:
- В данной модели две эндогенные переменные (
и
) и две экзогенные переменные (
и
). Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1 + 1.
Первое уравнение сверхидентифицировано, так как в нем на параметры при 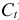
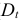
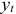
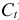
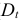
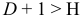
- Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.
Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной 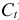
подставим значения 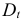
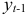
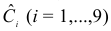
Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения 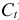
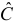
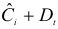
Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную 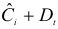
Пример задачи с уравнением №4.2.4.
Рассматривается следующая модель:
— расходы на потребление в период
;
— совокупный доход период
:
— инвестиции в период
;
— процентная ставка в период
;
— денежная масса в период
;
— государственные расходы в период
;
— расходы на потребление в период
;
— инвестиции в период
;
— текущий период;
— предыдущий период;
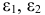
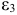
В предположении, что имеются временные ряды данных по всем переменным модели, предложить способ оценки ее параметров.
Как изменится ваш ответ на вопрос п. 1, если из модели исключить тождество дохода?
Решение:
- Модель представляет собой систему одновременных уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает четыре эндогенные переменные 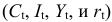
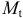
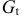
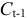
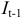
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 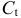
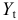
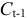
Это уравнение включает две эндогенные переменные 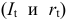
3-е уравнение тоже включает две эндогенные переменные 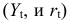
Это уравнение представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет.
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее числа эндогенных переменных модели минус 1, т. е. 4-1=3.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 1-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 2-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен трем, так как имеется квадратная подматрица 3×3 этой матрицы, определитель которой не равен нулю.
Достаточное условие идентификации для 3-го уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицированы. Для оценки параметров каждого из уравнений будем применять двухшаговый МНК.
Шаг 1. Запишем приведенную форму модели в общем виде
где 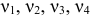
Определим параметры каждого из приведенных выше уравнений в отдельности обычным МНК. Затем найдем расчётные значения эндогенных переменных 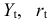
Шаг 2. В исходных структурных уравнениях заменим эндогенные переменные, выступающие в качестве факторных признаков, их расчетными значениями
Применяя к каждому из полученных уравнений в отдельности обычный МНК, определим структурные параметры
Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на 1 (из модели будет исключена переменная 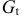
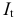
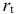
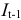
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

ПРИМЕНЕНИЕ ЭЛЕМЕНТОВ ЛИНЕЙНОЙ АЛГЕБРЫ К РЕШЕНИЮ ЭКОНОМИЧЕСКИХ ЗАДАЧ
Аннотация: в работе рассмотрены способы применения линейной алгебры при решении многих экономических задач. Экономика и линейная алгебра неразрывно связаны между собой. Тем самым применение различных математических методов значительно упрощает решение многих задач экономики.
Ключевые слова: линейная алгебра, экономика, матрицы, системы линейных алгебраических уравнений, метод Гаусса.
APPLICATION OF LINEAR ALGEBRA WITH THE SOLUTION OF THE ECONOMIC PROBLEMS
Verevkina D.S., student I -IEF-3, Smirnovа L.N., docent, SamGTU
State technical university, Samara
Annotation: Work examines the methods of application of linear algebra with the solution of many economic problems. The economy and linear algebra is inseparably connected together. Thus the application of different mathematical methods considerably simplifies the solution of many problems of the economy.
Keywords: linear algebra, the economy, matrix, the system of linear algebraic equations, the method of Gauss. Математика всегда была неразрывно связана с другими науками. Такая связь, прежде всего, обуславливается благодаря тому, что сама математика разделена на ряд отдельных и самостоятельных областей. Законы окружающего нас мира сами по себе универсальны. Математический язык тоже по-своему универсален.
На развитие и функционирование нашего общества влияет ряд основных причин. Эти причины рассматривает такая наука, как экономика. Экономика применяет различные количественные характеристики, а потому включает в себя множество математических методов. Одним из таких является линейная алгебра[1].
В линейной алгебре имеются различные методы решения задач. Основным и наиболее актуальным на сегодняшний день методом является применение элементов алгебры матриц. Особенно широко и часто его используют при разработке и использовании баз данных, в которых весь материал содержится и обрабатывается исключительно в форме матриц. Это делает задачи более простыми, а материал указан в более компактной и удобной матричной форме.
Таким образом, применение элементов линейной алгебры в значительной степени упрощает и делает более понятными методы решения многих задач экономики. Матрицей называется прямоугольная таблица чисел, в которой указываются её размеры в виде пары чисел m, n, где m – число строк в матрице, а n – число столбцов. Матрицы обозначается заглавной латинской буквой. Записывается матрица в следующих скобках: (A), [A], ║A║. Матрицы часто применяют во многих областях самых различных наук. Одна из таких наук — экономика. На примерах мы наглядно увидим преимущество использования матриц при решении многих экономических задач [3,4].
Данная задача наглядно показывает, что применение матриц упрощает решение подобных задач в несколько раз. Однако стоит учитывать, что в данном примере указаны всего несколько видов продукции и два вида сырья, тогда как на предприятиях количество видов продукции или сырья могут достигать значительных величин.
Кроме применения матриц, в экономике многие задачи решают с помощью системы линейных алгебраических уравнений (СЛАУ).
Один из методов решения СЛАУ — это метод Гаусса[3] или метод последовательного исключения переменных. Система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
У предприятия имеется определенный тип материала, из которого по плану необходимо выкроить 360 заготовок штор типа А (бязь), 300 заготовок типа B (шелк) и 675 заготовок штор типа C (органза). Для этого можно использовать три различных способа раскроя. На основе данных составляем таблицу:
🔍 Видео
Решение системы уравнений методом Крамера.Скачать

Решение системы уравнений методом ГауссаСкачать

Матричный метод решения систем уравненийСкачать

Решение систем уравнений методом подстановкиСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Решение системы уравнений в ExcelСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Математика это не ИсламСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Экономика. Альтернативные издержки. Построение КПВ, уравнение КПВ, сложение линейных КПВСкачать

10. Метод Крамера решения систем линейных уравнений.Скачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать


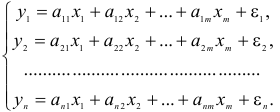
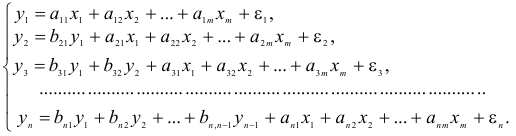
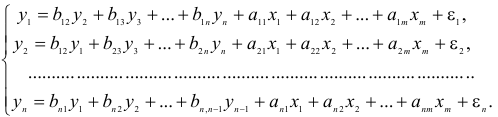
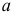 и
и 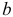 при переменных — структурные коэффициенты модели.
при переменных — структурные коэффициенты модели.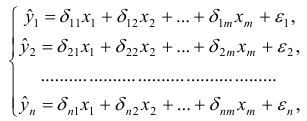
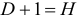 ;
;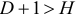 ;
;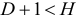 .
.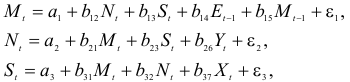

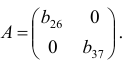
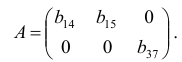
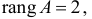
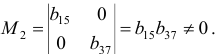
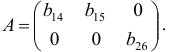
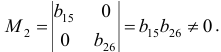
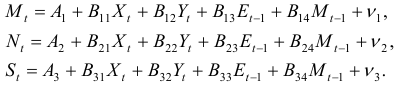
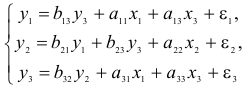
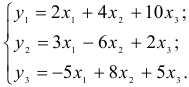

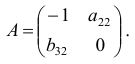
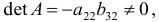
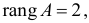
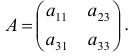
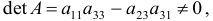
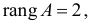
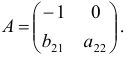
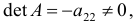
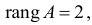
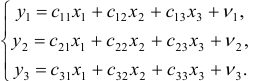
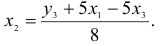
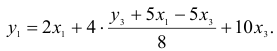
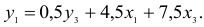
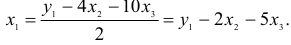
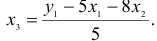
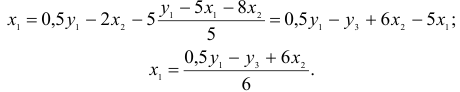
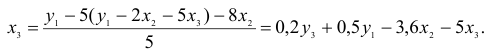
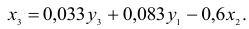
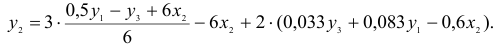
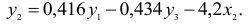
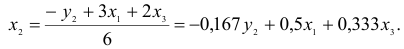
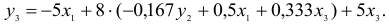
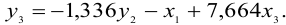
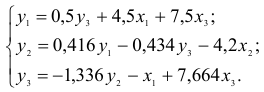
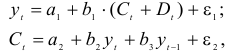
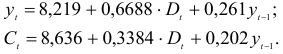
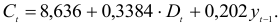
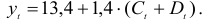
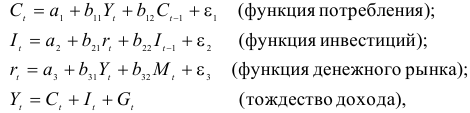
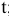 ;
;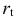 — процентная ставка в период
— процентная ставка в период 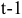 ;
;