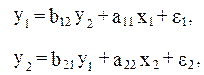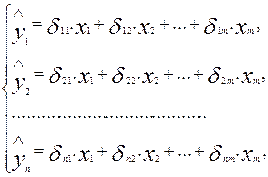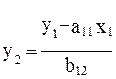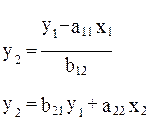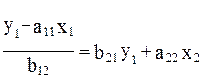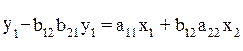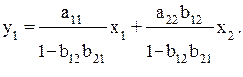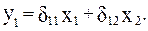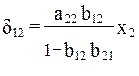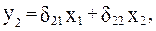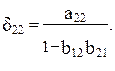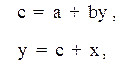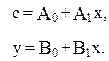Линейные модели из одновременных уравнений

Видео:Системы одновременных эконометрических уравненийСкачать

Система линейных одновременных уравнений. Структурная и приведенная формы эконометрической модели.

Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные обозначены в приведенной ранее системе одновременных уравнений как у. Это зависимые переменные, число которых равно числу уравнений в системе.

Экзогенные переменные обозначаются обычно как x. Это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них.

Простейшая структурная форма модели имеет вид:

где y – эндогенные переменные;

x – экзогенные переменные.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные).

Так, потребление текущего года (y_t) может зависеть не только от ряда экономических факторов, но и от уровня потребления в предыдущем году (y_t-1)

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

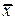
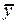
Структурная форма модели в правой части содержит при эндогенных и экзогенных переменных коэффициенты b_i и a_j, (b_i – коэффициент при эндогенной переменной, a_j – коэффициент при экзогенной переменной), которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонения от уровня, т. е. под x подразумевается x- а под y — соответственно у- . Поэтому свободный член в каждом уравнении системы отсутствует.

Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные структурных коэффициентов модели структурная коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

где 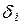— коэффициенты приведенной формы модели.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели ( ) через коэффициенты структурной модели (a_j и b_i). Для упрощения в модель не введены случайные переменные.

Для структурной модели вида

и (4.1)

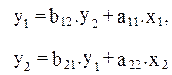
Приведенная форма модели имеет вид

и (4.2)

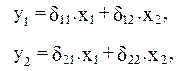
В которой y₂ из первого уравнения структурной модели можно выразить следующим образом:

Тогда система одновременных будет представлена как

Отсюда имеем равенство:

Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения приведенной формы модели:

Из уравнения следует, что коэффициенты приведенной формы модели представляют собой нелинейные соотношения коэффициентов структурной модели, т. е.

и

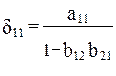
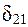
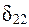
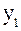
Аналогично находятся и коэффициенты приведенной формы модели второго уравнения системы ( и ) также нелинейно связаны с коэффициентами структурной модели. Для этого выразим переменную из второго структурного уравнения и подставим во второе.

Что соответствует уравнению приведенной формы модели:

и

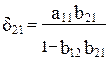
Эконометрические модели обычно включают в систему не только уравнения, отражающие взаимосвязи еменную им турнвязаны с коэффодели второго уравнения системы ()дели в виде уравнения приведенной формы модели:

между отдельными переменными, но и выражения тенденции развития явления, а также разного рода тождества. Так, в 1947 г., исследуя линейную зависимость потребления (c) от дохода (y), Т. Хавельмо предложил одновременно учитывать тождество дохода. В этом случае модель имеет вид:

где х – инвестиции в основной капитал и запасы экспорта и импорта;

a и b – параметры линейной зависимости c от y.

Их оценки должны учитывать тождество дохода в отличие от параметров обычной линейной регрессии.

В этой модели две эндогенные переменные – c и y и одна экзогенная переменная x. Система приведенных приведенных уравнений составит:

Она позволяется получить значения эндогенной переменной с через переменную х. Рассчитав коэффициенты приведенной формы модели (A₀, A₁, B₀, B₁), можно перейти к коэффициентам структурной модели a и b, подставляя в первое уравнение приведенной формы выражение переменной x из второго уравнения приведенной формы модели. Приведенная форма модели хотя и значения экзогенных переменных, аналитически уступает структурной форме модели, так в ней отсутствуют оценки взаимосвязи между эндогенными переменными.

Дата добавления: 2016-05-16 ; просмотров: 1370 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Система одновременных эконометрических уравнений

Вы будете перенаправлены на Автор24

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Общие сведения о системе одновременных эконометрических уравнений

Система одновременных экономических уравнений – это совокупность уравнений, которые позволяют исследователям установить наличие и степень связи (взаимозависимости) между эконометрическими переменными.

Выделяют две группы экономических переменных, из которых образуют эконометрические уравнения:

• эндогенные переменные, чьи значения определяют в результате функционирования изучаемой экономической системы (эндогенные переменные зависят как от экзогенных, так и от других эндогенных переменных);
• экзогенные переменные, чьи значения задаются извне (т.е. определяются вне эконометрической модели) и являются основой для определения значений эндогенных переменных (экзогенные переменные являются независимыми).

Функционирование сложных экономических систем может быть объяснено благодаря построению изолированных уравнений регрессии и измерению на их основе тесноты связи между переменными. Однако истинное влияние отдельных признаков на вариацию результирующей переменной не может быть описано одним отдельно взятым уравнением регрессии. В связи с этим в изучении экономических процессов важное значение приобрело структурирование связей между системой переменных.

В качестве примера системы одновременных эконометрических уравнений можно привести простейшую макроэкономическую (кейнсианскую) модель, которая состоит из двух уравнений:

В данной модели эндогенными переменными являются C (расходы на потребление) и Y (доход), а экзогенной переменной – I (инвестиции). b представляет собой коэффициент, который выражает предельную склонность к потреблению.

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Характеристика структурной и приведенной форм системы уравнений

Данная система от всех других систем уравнения отличается наличием определенной структурной формы эконометрической модели. Это форма предполагает, что в правых и левых частях разных уравнений системы находятся одни и те же экономические переменные. Структурная форма системы одновременных эконометрических уравнений в случае переноса всех эндогенных переменных в левую часть может быть представлено в следующем матричном виде: YA = XB + E.

Готовые работы на аналогичную тему

Кроме структурной также выделяют приведенную (прогнозную) форму системы. По сути она есть представление системы, в котором эндогенные переменные выражены через экзогенные, то есть в каждом уравнении имеется только одна эндогенная переменная. Тогда она выглядит так: Y = XП + U.

Приведенную форму системы всегда можно получить, если задана структурная форма. Однако обратное действие не всегда возможно, а если оно и возможно, то не всегда получается однозначный результат.

Если через коэффициенты приведенной формы можно выразить коэффициенты структурного уравнения, то оно называется идентифицируемым (в противном случае оно – неидентифицируемое). Точная индентифицируемость свойственна ситуации, когда способ подобного выражения является единственным. Если же их несколько, то говорят о сверхидентифицируемости.

Чтобы имела место идентифицируемость, требуется выполнение такого необходимого условия, как непревышение количества переменных правой части уравнения над количеством всех экзогенных переменных системы. Формулировка этого условия может отличаться. Так, часто говорят: количество экзогенных переменных, которые исключены из данного уравнения, должно быть не меньше количества эндогенных переменных, которые включены в уравнение, за вычетом единицы.

Также выделяют условие, достаточное для признания идентифицируемости системы. Оно заключается в том, чтобы общее число эндогенных переменных системы за вычетом единицы не превышало ранг матрицы, который составлен из коэффициентов (в других уравнениях) при переменных, отсутствующих в данном уравнении.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Методы оценки систем одновременных эконометрических уравнений

Для того, чтобы оценить представленные в структурной форме уравнения системы, нецелесообразно непосредственно применять обычный метод наименьших квадратов. Это связано с тем, что подобное применение нарушит важнейшее условие регрессионного анализа — экзогенность (предопределенность, независимость) факторов. Тогда будут получены смещённые и несостоятельные оценки параметров.

Поэтому системы одновременных эконометрических уравнений оценивают посредством применения следующих методов:

• косвенный метод наименьших квадратов – подстановка в аналитическое выражение зависимости структурных коэффициентов от их приведённых оценок, которые получают в результате применения обычного метода наименьших квадратов;
• двухшаговый метод наименьших квадратов – оценивание сначала зависимости эндогенных переменных от всех экзогенных (первый шаг), а затем – структурной формы модели, в которой эндогенные переменные заменены на их оценки, полученные на первом шаге (второй шаг);
• трехшаговый метод наименьших квадратов – предыдущий метод дополняется третьим шагом, с помощью которого оценивают ковариационную матрицу вектора случайных ошибок системы уравнений;
• методы максимального правдоподобия – использование всей информации об ограничениях на приведённую форму эконометрической модели.

Видео:09 05 Общая линейная модельСкачать

Эконометрика, её задача и метод. Эконометрические модели и два принципа их спецификации (стр. 22 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Это так называемая неограниченная приведённая форма. Структурную форму можно записать следующим образом:

Это так называемая ограниченная приведённая форма, то есть приведённая форма с ограничением на коэффициенты следующего вида: .

Если задана структурная форма, то всегда можно получить ограниченную приведённую форму (предполагается, что матрица А невырождена). Однако, обратное не всегда возможно, а если возможно, то не всегда однозначно.

Структурное уравнение называется идентифицируемым, если его коэффициенты можно выразить через коэффициенты приведённой формы. Если это можно сделать единственным способом, то говорят о точной индентифицируемости, если несколькими способами — о сверхидентифицируемости. В противном случае оно называется неидентифицируемым. Сверхидентифицируемость фактически означает, что на коэффициенты приведённой формы наложены некоторые ограничения (сверхидентифицирующие). В полной приведённой форме участвуют все экзогенные переменные и на коэффициенты не налагается никаких ограничений.

Необходимое условие идентифицируемости структурного уравнения (порядковое условие): количество переменныхправой части уравнения должно быть не больше количества всех экзогенных переменных системы. В канонической форме (когда «левой» и «правой» частей нет) данное условие иногда формулируют следующим образом: количество исключенных из данного уравнения экзогенных переменных должно быть не меньше количества включенных эндогенных переменныхуравнения минус единица. Если данное условие не выполнено, то уравнение неидентифицируемо. Если выполнено со знаком равенства, то, вероятно, точно идентифицируемо, иначе — сверхидентифицируема.

Достаточное условие идентифицируемости структурного уравнения: ранг матрицы, составленной из коэффициентов (в других уравнениях) при переменных, отсутствующих в данном уравнении, не меньше общего числа эндогенных переменных системы минус единица.

Простейшая макроэкономическая (кейнсианская) модель

Здесь C и Y — потребление (потребительские расходы) и доход — эндогенные переменные модели, I — инвестиции — экзогенная переменная модели, b — предельная склонность к потреблению

Приведённая форма модели имеет вид:

Величина называется мультипликатором инвестиций (единица увеличения инвестиций приводит к существенно большему изменению дохода).

Можно проверить порядковое условие идентифицируемости. В первом уравнении в правой части 1 эндогенная переменная и нет экзогенных переменных (без учета константы). Всего экзогенных переменных в модели — 1 (тоже без константы). Таким образом, порядковое (необходимое) условие идентифицируемости выполнено.

Видно, что приведённая форма является ограниченной с двумя ограничениями и .

40. Эконометрические модели из одновременных уравнений. Нарушение предпосылки теоремы Гаусса-Маркова о некоррелированности объясняющих переменных и случайных возмущений как источник несостоятельности мнк-оценок параметров (на примере простой кейнсианской модели формирования доходов).

Существуют несколько методов вычисления состоятельных оценок параметров линейной модели множественной регрессии в условиях нарушения четвертой предпосылки теоремы Гаусса-Маркова.

Наиболее практичный метод — метод применения инструментальных переменных. В его основе лежит понятие инструментальной переменной.

Определение. Пусть имеется модель линейной множественной регрессии

(1)

в которой объясняющие переменные коррелируют в пределе со случайными возмущениями .То есть не выполняется условие состоятельности МНК-оценок параметров модели о том, что существует и равен предел по вероятности: ). Переменные называются инструментальными для модели (1), если они удовлетворяют двум требованиям:

1. Существует предел

2. Существует невырожденная матрица:

Из определения следует, что инструментальные переменные в пределе коррелируют с исходными регрессорами , но не коррелируют в пределе со случайными возмущениями. Z и Х матрицы размерностью n×K, составленные по результатам наблюдений за соответствующими переменными.

Теорема. Процедура доставляет состоятельные оценки параметров модели (1).

41. Использование инструментальных переменных при идентификации поведенческих уравнений модели в структурной форме.

В основе метода применения инструментальных переменных для вычисления состоятельных оценок параметров линейной модели множественной регрессии в условиях нарушения четвертой предпосылки теоремы Гаусса-Маркова лежит понятие инструментальной переменной. Определение. Пусть имеется модель линейной множественной регрессии

Yt=a1x1t + a2x2t + akxkt + ut

M(ut) = 0; σ2(ut) = σ2u

В которой объясняющие переменные коррелируют в пределе со случайными возмущениями ut. Переменные (z1t, z2t,…,zkt) называются инструментальными для модели, приведенной выше, если они соответствуют двум требованиям:

Plimn→∞((1/n)ZTu) = 0

Существует невырожденная матрица:

Заметим, что инструментальные переменные в пределе коррелируют с исходными регрессорами, но не коррелируют со случайными возмущениями.

доставляет состоятельные оценки параметров модели 1.

Таким образом, инструментальные переменные используются в косвенном методе наименьших квадратов и двухшаговом методе наименьших квадратов для идентификации поведенческих уравнений модели в их структурной форме.

41.52. Эконометрические модели из одновременных уравнений. Процедура двухшагового метода наименьших квадратов оценивания уравнения модели.

Если система одновременных уравнений сверхидентифицируема, то КМНК не используется, так как он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).

Алгоритм двухшагового метода наименьших квадратов реализуется в четыре этапа.

1. На основе структурной формы системы одновременных уравнений составляется ее приведенная форма.

2. Неизвестные коэффициенты каждого уравнения приведенной формы системы одновременных уравнений оцениваются традиционным методом наименьших квадратов.

3. Рассчитываются значения тех эндогенных переменных, которые выступают в качестве факторных переменных в сверхидентифицированном уравнении.

4. С помощью традиционного метода наименьших квадратов определяются все структурные коэффициенты уравнений системы через предопределенные переменные, входящие в это уравнение в качестве факторов, и значения эндогенных переменных, полученных на предыдущем шаге.

Метод получил название двухшагового МНК потому, что МНК используется дважды: на первом шаге при определении приведенной формы модели и на четвертом шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным расчетных значений эндогенных переменных.

🔍 Видео

Модель Леонтьева. Теория и решение задачи.Скачать

Парная регрессия: линейная зависимостьСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Линейная модель международной торговлиСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Алгебра 7 класс. Системы уравнения как модели реальных ситуацийСкачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Эконометрия_л9Скачать

ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Математика это не ИсламСкачать

Параметры с нуля до уровня ЕГЭ. Линейные уравнения. Математик МГУСкачать