Линейные и квадратные уравнения и неравенства и методы их решения

В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.

Видео:ЛИНЕЙНЫЕ НЕРАВЕНСТВА - Как решать линейные неравенства // Подготовка к ЕГЭ по МатематикеСкачать

Что представляет собой квадратное неравенство

Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.

Квадратное неравенство – это такое неравенство, которое имеет вид a · x 2 + b · x + c 0 , где a , b и c – некоторые числа, причем a не равно нулю. x – это переменная, а на месте знака может стоять любой другой знак неравенства.

Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида y = a · x 2 + b · x + c .

Приведем пример квадратного неравенства:

Возьмем 5 · x 2 − 3 · x + 1 > 0 . В этом случае a = 5 , b = − 3 и c = 1 .

Или вот такое неравенство:

− 2 , 2 · z 2 − 0 , 5 · z − 11 ≤ 0 , где a = − 2 , 2 , b = − 0 , 5 и c = − 11 .

Покажем несколько примеров квадратных неравенств:

Здесь коэффициенты этого квадратного неравенства есть ; 1 2 3 · x 2 — x + 5 7 0 , в этом случае a = 1 2 3 , b = — 1 , c = 5 7 .

Особое внимание нужно обратить на тот факт, что коэффициент при x 2 считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида b · x + c > 0 , так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты b и c могут быть равны нулю как вместе, так и по отдельности.

Пример такого неравенства x 2 − 5 ≥ 0 .

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Способы решения квадратных неравенств

Основным метода три:

• графический;
• метод интервалов;
• через выделение квадрата двучлена в левой части.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Графический метод

Метод предполагает проведение построения и анализа графика квадратичной функции y = a · x 2 + b · x + c для квадратных неравенств a · x 2 + b · x + c 0 ( ≤ , > , ≥ ) . Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.

Видео:8 класс, 40 урок, Решение линейных неравенствСкачать

Метод интервалов

Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a · x 2 + b · x + c при их наличии.

Для неравенства a · x 2 + b · x + c 0 решениями являются промежутки со знаком минус, для неравенства a · x 2 + b · x + c > 0 , промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.

Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Выделение квадрата двучлена

Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида ( x − p ) 2 q ( ≤ , > , ≥ ) , где p и q – некоторые числа.

Видео:Решение квадратных неравенств | МатематикаСкачать

Неравенства, сводящиеся к квадратным

К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.

Приведем пример. Рассмотрим равносильное преобразование неравенства 5 ≤ 2 · x − 3 · x 2 . Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида 3 · x 2 − 2 · x + 5 ≤ 0 .

Необходимо найти множество решений неравенства 3 · ( x − 1 ) · ( x + 1 ) ( x − 2 ) 2 + x 2 + 5 .

Решение

Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:

3 · ( x − 1 ) · ( x + 1 ) − ( x − 2 ) 2 − x 2 − 5 0 , 3 · ( x 2 − 1 ) − ( x 2 − 4 · x + 4 ) − x 2 − 5 0 , 3 · x 2 − 3 − x 2 + 4 · x − 4 − x 2 − 5 0 , x 2 + 4 · x − 12 0 .

Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.

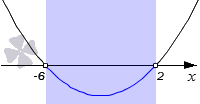
D ’ = 2 2 − 1 · ( − 12 ) = 16 , x 1 = − 6 , x 2 = 2

Построив график, мы можем увидеть, что множеством решений является интервал ( − 6 , 2 ) .

Ответ: ( − 6 , 2 ) .

Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2 · x 2 + 5 x 2 + 6 · x + 14

равносильно квадратному неравенству x 2 − 6 · x − 9 0 , а логарифмическое неравенство log 3 ( x 2 + x + 7 ) ≥ 2 – неравенству x 2 + x − 2 ≥ 0 .

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Линейные, квадратные и простейшие кубические уравнения. Примеры

Определение

Уравнение (с одной переменной) — это некоторое равенство двух выражений, содержащее неизвестную (переменную). [f(x)=g(x) qquad qquad (1)] Пусть для определенности все дальнейшие уравнения содержат переменную, обозначенную буквой (x) .

Замечание

Заметим, что (x) — это просто некоторое число, значение которого неизвестно.

Определение

Областью определения (или областью допустимых значений, сокращенно ОДЗ) любого уравнения вида ((1)) будем называть множество значений переменной (x) , при которых определены (то есть не теряют смысла) функции (f(x)) и (g(x)) .

Пример

Уравнение (dfrac =5) определено при всех значениях переменной (x) , кроме (x=1) , потому что в этом случае знаменатель дроби в левой части равенства обращается в ноль. Значит, ОДЗ уравнения (xin (-infty;1)cup(1;+infty)) .

Определение

Корнем уравнения называется то числовое значение (x) , при котором уравнение обращается в верное равенство.
Иногда корни уравнения называют решением этого уравнения.

Например, корнем уравнения из предыдущего примера является число (x=3) , потому как тогда уравнение принимает вид (dfrac=5) или, что то же самое, (5=5) , что является верным равенством.

Замечание

1) Заметим, что уравнение может как иметь корни, так и не иметь корней. Например, уравнение (dfrac 1x=0) ни при каких значениях (x) не может быть верным, потому что дробь равна нулю, когда ее числитель равен нулю, а знаменатель при этом не теряет смысла. У нашей дроби числитель (1ne 0) .

2) Фраза “решить уравнение” означает найти все корни данного уравнения или доказать, что корней нет.

Определение

Два уравнения равносильны (или эквивалентны), если они имеют одинаковые решения.
Например, уравнения (x=3) и (3x=6+x) эквивалентны, т.к. оба имеют единственное решение (x=3) .

Эквивалентность уравнений обозначается так: (x=3 quad Leftrightarrow quad 3x=6+x) .

Свойства уравнений

1. В любом уравнении можно переносить слагаемые из одной части равенства в другую, при этом меняя их знак на противоположный. При этом полученное уравнение равносильно исходному.
Например, уравнение (x+4=2x^2) можно переписать в виде (x+4-2x^2=0) .

2. В любом уравнении можно правую и левую части умножать или делить на одно и то же число, не равное нулю. При этом полученное уравнение равносильно исходному.
Например, уравнение (0,5x=-2) равносильно уравнению (x=-4) , которое получено из исходного путем умножения обеих частей на (2) .

3. В любом уравнении можно к правой и левой частям прибавлять одно и то же число. При этом полученное уравнение равносильно исходному.
Например, уравнение (x+2=5x^2) после прибавления к обеим частям (-2) примет вид (x=5x^2-2) .

[<Large<text>>] Линейное уравнение – это уравнение вида [ax + b = 0qquad qquad (2)] где (ane 0,b) – числа, или уравнение, к нему сводящееся.

ОДЗ линейного уравнения ((2)) — все (x inmathbb) .

Линейное уравнение (ax+b=0) преобразуется в (ax=-b) и всегда имеет единственное решение (x=-dfrac ba) .
Например, (2x-4=0) имеет корень (x=2) . Замечание: при переносе слагаемых из одной части равенства в другую знак слагаемого меняется на противоположный. Например, выражение (x-5=8) преобразуется в выражение (x=8+5) .
Знак, стоящий перед слагаемым – это и есть его знак, то есть в выражении (x-5) два слагаемых: (x) и (-5) . Если перед слагаемым не стоит никакого знака, то подразумевается, что перед ним стоит знак “ (+) ”.

[<Large<text>>] Квадратное уравнение – это уравнение вида [ax^2+bx+c=0 qquad qquad (3)] где (a, b, c) – числа, причем (ane 0) , или уравнение, к нему сводящееся.

Число (a) называется старшим (первым) коэффициентом, число (b) – вторым коэффициентом, число (c) – свободным членом.

Замечание

1) Заметим, что если (a=0) , то уравнение ((3)) становится линейным; именно поэтому в определении (ane 0) .

2) Выражение (ax^2+bx+c) называется квадратичным (квадратным) трехчленом.

ВАЖНО! Обращаем ваше внимание на то, что, например, в квадратном трехчлене (7-x^2+2x) коэффициент (a=-1) , (b=2) и (c=7) ! Так как (7-x^2+2x=-x^2+2x+7) , а по определению (a) – коэффициент перед (x^2) , (b) – коэффициент перед (x) , (c) – свободный член.

Определение

Дискриминантом квадратного уравнения ((3)) называется выражение (D=b^2-4ac) .

Корни квадратного уравнения

1) Если дискриминант квадратного уравнения больше нуля ( (D>0) ), то оно имеет два различных корня [x_1=dfrac qquad text qquad x_2=dfrac]

2) Если дискриминант квадратного уравнения равен нулю ( (D=0) ), то оно имеет два совпадающих корня (часто говорят, что оно имеет один корень) [x=-dfrac b]

3) Если дискриминант квадратного уравнения меньше нуля ( (D ), то оно не имеет корней.

Пример:
Решите уравнение [3x^2 — 33x + 90 = 0.]

Решение.
Найдём дискриминант данного уравнения: [D = 33^2 — 4cdot 3cdot 90 = 9] Следовательно, уравнение имеет два различных корня, равных [x_1=dfrac = 6 qquad text qquad x_2=dfrac = 5]

Теорема Виета

Пусть квадратное уравнение (ax^2 + bx + c = 0) , (aneq 0) , имеет два корня (x_1) и (x_2) (возможно, совпадающих), то есть (Dgeqslant 0) . Тогда их сумма равна [x_1+x_2=-dfrac] а их произведение равно [x_1cdot x_2=dfrac]

Доказательство

Определение

Квадратное уравнение называется приведенным, если старший коэффициент (a=1) .
Любое квадратное уравнение можно сделать приведенным: для этого необходимо разделить уравнение на (a) .

Следствие

Для приведенного квадратного уравнения (x^2+px+q=0) теорема Виета выглядит следующим образом: [x_1+x_2=-p, qquad qquad x_1cdot x_2=q]

Теорема: разложение на множители квадратного трехчлена

Пусть уравнение (ax^2 + bx + c = 0) , (aneq 0) , имеет два корня (возможно, совпадающих), то есть (Dgeqslant 0) . Тогда при любом значении (x) выполнено [ax^2 + bx + c = a(x — x_1)(x — x_2),] где (x_1) и (x_2) – корни уравнения (ax^2 + bx + c = 0) (возможно, совпадающие).

Доказательство

Сделаем преобразования: [begin &a(x-x_1)(x-x_2)=aleft(x — dfrac<-b + sqrt>right)left(x — dfrac<-b — sqrt>right) =aleft(x^2 — xleft(dfrac<-b + sqrt> + dfrac<-b — sqrt>right) + dfracright)=\[2ex] &=aleft(x^2-xcdot left(-dfrac baright)+dfracright) =a(x^2+dfrac ba x+dfrac ca)=ax^2+bx+c end]

Пример

Разложить на множители квадратный трехчлен (3x^2-2x-1) .

Решение.
Рассмотрим уравнение (3x^2-2x-1=0) и найдем его корни.
(D=(-2)^2-4cdot 3cdot (-1)=16) , значит

Таким образом, (3x^2-2x-1=3(x-1)(x+frac13)=(x-1)(3x+1)) .

[<Large<text>>] (bullet) Кубический корень из числа (a) – это такое число (b) , которое при возведении в куб равно (a) : [sqrt[3] a=bquad textquad a=b^3] (bullet) Таблица кубов чисел от 1 до 10: [begin hline 1^3=1 & quad6^3=216 \ 2^3=8 & quad7^3=343\ 3^3=27 & quad8^3=512\ 4^3=64 & quad9^3=729\ 5^3=125 & quad10^3=1000\ hline end] (bullet) Простейшие кубические уравнения – уравнения, сводящиеся к виду [x^3=a] Для любого числа (a) такие уравнения имеют единственный корень [x=sqrt[3]a] Пример:
1) решением уравнения (x^3=-8) является (x=sqrt[3]=-2) .
2) решением уравнения (x^3=64) является (x=4) .

Теория линейных и квадратных уравнений традиционно изучается школьниками Москвы и других городов в 8 классе. И хотя данная тема рассматривается в рамках образовательного курса достаточно подробно, и ей отводится немало времени, с заданиями из этого раздела выпускники не всегда справляются с легкостью. Именно поэтому, готовясь к сдаче ЕГЭ, учащимся непременно стоит освежить в памяти теорию и разобраться в решении задач с линейными и квадратными уравнениями.

Сделать это легко, оперативно и эффективно вам позволит образовательный портал «Школково». Всю необходимую теорию по теме «Квадратные и линейные уравнения» для подготовки к ЕГЭ вы можете найти в соответствующем разделе. Весь базовый материал составлен нашими специалистами на основе многолетнего опыта и представлен в максимально доступной форме. Изучив определения, формулы и основные свойства линейных и квадратных уравнений, учащиеся смогут не только вспомнить всею необходимую теорию, но и грамотно объяснить принцип решения задач ЕГЭ. Закрепить усвоенный материал вам помогут упражнения в разделе «Каталог». Здесь вы можете найти как простые, так и более сложные задачи по данной теме. Для каждого задания на сайте наши специалисты прописали подробный алгоритм решения и правильный ответ.

Изучить теорию по теме «Линейные и квадратные уравнения» и попрактиковаться в выполнении упражнений можно в режиме онлайн. При необходимости любое задание можно сохранить в «Избранное», чтобы в дальнейшем можно было к нему вернуться или обсудить с преподавателем.

Видео:Линейные и квадратные неравенстваСкачать

Повторение и систематизация курса алгебры 7-9 класса. Уравнения, неравенства и их системы. Часть 1. Решение линейных и квадратных уравнений

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы повторим и систематизируем наши знания об уравнениях, неравенствах и их системах, а также о методах их решениях.

🎦 Видео

Как решать неравенства? 9 - 11 класс. Вебинар | Математика TutorOnlineСкачать

Как решать линейные и квадратные уравненияСкачать

Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Как решать неравенства? Часть 1| МатематикаСкачать

КВАДРАТНЫЕ НЕРАВЕНСТВА ПОНЯТНЫМ ЯЗЫКОМСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

ЧТО ТАКОЕ МЕТОД ИНТЕРВАЛОВ? ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэ #методинтерваловСкачать

Алгебра 9. Урок 4 - Неравенства линейные - решение.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Алгебра 10 класс (Урок№3 - Квадратные уравнения, неравенства и их системы.)Скачать