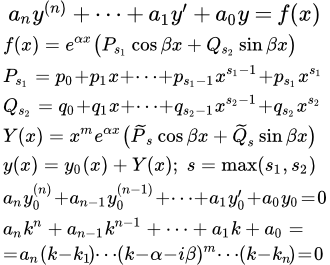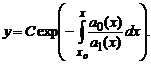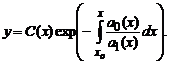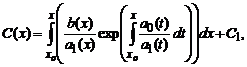Дифференциальное уравнение называется линейным, если в нём функция и все её производные содержатся только в первой степени, отсутствуют и их произведения.
Общий вид линейного дифференциального уравнения первого порядка таков:
,
где 
и 
— непрерывные функции от x.
Как решить линейное дифференциальное уравнение первого порядка?
Интегрирование такого уравнения можно свести к интегрированию двух двух дифференциальных уравнений первого порядка с разделяющимися переменными. Великие математики доказали, что нужную функцию, то есть решение уравнения, можно представить в виде произведения двух неизвестных функций u(x) и v(x). Пусть y = uv, тогда по правилу дифференцирования произведения функций
и линейное дифференциальное уравнения первого порядка примет вид
. (*)
Выберем функцию v(x) так, чтобы в этом уравнении выражение в скобках обратилось в нуль:
,
то есть в качестве функции v берётся одно из частных решений этого уравнения с разделяющимися переменными, отличное от нуля. Разделяя в уравнении переменные и выполняя затем его почленное интегрирование, найдём функцию v. Так как функция v — решение уравнения, то её подстановка в уравнение даёт
.
Таким образом, для нахождения функции u получили дифференциальное уравнение первого порядка с разделяющимися переменными. Найдём функцию u как общее решение этого уравнения.
Теперь можем найти решение исходного линейного дифференциального уравнения первого порядка. Оно равно произведению функций u и v, т. е. y = uv. u и v уже нашли.
Пример 1. Решить линейное дифференциальное уравнение первого порядка
.
Решение. Как было показано в алгоритме, y = uv. Подставляя выражения для 
и y в уравнение вида (*), получим
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
или 
.
После разделения переменных это уравнение принимает вид
.
Почленное интегрирование даёт
Подставив найденное значение функции v в равенство (* *), получим
.
и, интегрируя находим u:
Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:
Как видим, всё решение выполняется точным следованием алгоритму, приведённому в начале статьи. Меняются лишь виды функций в уравнениях. Степени, корни, экспоненты и т.д. Это чтобы алгоритм отпечатался в памяти и был готов к разным случаям, которые только могут быть на контрольной и экзамене. А кому стало скучно, наберитесь терпения: впереди ещё примеры с интегрированием по частям!
Важное замечание. При решении заданий не обойтись без преобразований выражений. Для этого требуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Пример 2. Решить линейное дифференциальное уравнение первого порядка
.
Решение. Подставляя выражения для и y в уравнение вида (*), получим
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
.
После разделения переменных это уравнение принимает вид
.
Почленное интегрирование даёт
Подставив найденное значение функции v в равенство (* *), получим
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные:
и, интегрируя находим u:
Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:
В следующем примере — обещанная экспонента.
Пример 3. Решить линейное дифференциальное уравнение первого порядка
.
Решение. Подставляя выражения для и y в уравнение вида (*), получим
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
или 
.
После разделения переменных это уравнение принимает вид
.
Почленное интегрирование даёт
Подставив найденное значение функции v в равенство (* *), получим
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находимu:
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
Любители острых ощущений дождались примера с интегрированием по частям. Таков следующий пример.
Пример 4. Решить линейное дифференциальное уравнение первого порядка
.
Решение. В этом случае сначала нужно добиться, чтобы производная «игрека» ни на что не умножалась. Для этого поделим уравнение почленно на «икс» и получим
.
Подставляя выражения для и y в уравнение вида (*), получим
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
или 
.
После разделения переменных это уравнение принимает вид
.
Почленное интегрирование даёт
Подставив найденное значение функции v в равенство (* *), получим
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируем по частям.
В интеграле 
, 
.
Тогда 
.
Интегрируем и находим u:
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
И уж совсем странной статья о дифференциальных уравнениях была бы без примера с тригонометрическими функциями.
Пример 5. Решить линейное дифференциальное уравнение первого порядка
.
Решение. Подставляя выражения для и y в уравнение вида (*), получим
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
или 
.
После разделения переменных это уравнение принимает вид
.
Почленное интегрирование даёт
Подставив найденное значение функции v в равенство (* *), получим
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
В последних двух примерах требуется найти частное решение уравнения.
Пример 6. Найти частное решение линейного дифференциальное уравнение первого порядка
при условии 
.
Решение. Чтобы производная «игрека» ни на что не умножалась, разделим уравнение почленно на 
и получим
.
Подставляя выражения для и y в уравнение вида (*), получим
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
или 
.
После разделения переменных это уравнение принимает вид
.
Почленное интегрирование даёт
Подставив найденное значение функции v в равенство (* *), получим
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
Найдём частное решение уравнения. Для этого в общее решение подставим 
и 
и найдём значение C:
Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:
.
Пример 7. Найти частное решение линейного дифференциального уравнения первого порядка
при условии 
.
Перенесём функцию «игрека» в левую часть и получим
.
Подставляя выражения для и y в уравнение вида (*), получим
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
или 
.
После разделения переменных это уравнение принимает вид
.
Почленное интегрирование даёт
Подставив найденное значение функции v в равенство (* *), получим
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:
.
Первый интеграл равен 
, второй находим интегрированием по частям.
В нём 
, 
.
Тогда 
, 
.
Находим второй интеграл:
.
В результате получаем функцию u:
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
Найдём частное решение уравнения. Для этого в общее решение подставим 
и 
и найдём значение C:
Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:
.
Выводы. Алгоритм решения линейных дифференциальных уравнений первого порядка достаточно однозначен. Трудности чаще всего возникают при интегрировании и это означает, что следует повторить этот обширный раздел математического анализа. Кроме того, что особенно видно из примеров ближе к концу статьи, очень важно владеть приёмами действий со степенями и дробями, а это школьные темы, и если они подзабыты, то их тоже следует повторить. Совсем простых «демо»-примеров ждать на контрольной и на экзамене не стоит.
- Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью
- Определение общего решения по известному частному решению
- Метод решения линейных ДУ с постоянными коэффициентами со специальной неоднородной частью
- Установление вида частного решения
- Частные случаи
- Неоднородность в виде многочлена
- Неоднородность в виде произведения экспоненты и многочлена
- Неоднородность в виде суммы произведений многочленов на косинус и синус
- Линейные уравнения первого порядка
- 🎥 Видео
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью
Видео:Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать
Определение общего решения по известному частному решению
Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) ,
где – действительные числа; – действительная функция. Если известно частное (любое) решение уравнения (1), то можно найти его общее решение по формуле:
,
где – общее решение однородного уравнения:
.
Если неоднородная часть может быть представлена в виде суммы функций:
,
то частное решение также может быть представлено в виде суммы частных решений:
,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций :
.
Как правило, легче найти частные решения от более простых неоднородных частей, а затем получить частное решение для всего уравнения суммированием полученных частных решений.
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать
Метод решения линейных ДУ с постоянными коэффициентами со специальной неоднородной частью
Рассмотрим линейное неоднородное уравнение со специальной неоднородной частью в виде комбинации многочленов, экспоненты, синусов и косинусов:
(2) ,
где – многочлены степеней и , соответственно:
;
;
– известные коэффициенты.
Это уравнение можно решить общим методом понижения порядка. Однако существует более простой способ, основанный на том, что частное решение такого уравнения имеет определенный вид. Суть этого метода заключается в следующем.
Вначале ищем общее решение однородного уравнения:
(3) .
Далее устанавливаем вид частного решения исходного уравнения (2). Оно выражается через многочлены, экспоненту, синусы и косинусы, которые входят в частное решение с неизвестными коэффициентами. Установив вид частного решения, подставляем в уравнение (2). Приравнивая левую и правую части, находим неизвестные коэффициенты.
После этого общее решение исходного уравнения (2) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
.
Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать
Установление вида частного решения
Установим вид частного решения уравнения (2). Для этого вначале ищем решение однородного уравнения (3) в виде . В результате, для k , получаем уравнение, которое называется характеристическим уравнением:
(4) .
Решаем это уравнение. Получаем n корней . Тогда характеристическое уравнение (4) можно представить в виде произведения множителей:
(5) .
Часть корней (или все) в (5) могут быть комплексными. Поэтому выразим корень через действительную и мнимую части:
.
Для действительного корня .
Некоторые корни в (5) могут быть кратными:
.
Здесь p – кратность корня. Кратный корень кратности p входит в произведение (5) в виде множителя .
Если среди корней характеристического уравнения (4) нет корня со значением
,
то частное решение уравнения (2) имеет вид:
,
где – наибольшее из и .
,
– многочлены степени s с неизвестными коэффициентами , которые подлежат определению подстановкой в уравнение (2).
Если среди корней характеристического уравнения (4) есть корень кратности p со значением
то частное решение уравнения (2) имеет вид:
,
где также – наибольшее из и .
,
– многочлены степени s с неизвестными коэффициентами .
Когда вид частного решения установлен, подставляем Y в уравнение (2) и находим неизвестные коэффициенты , приравнивая левую и правую части уравнения. После чего получаем общее решение уравнения (2):
.
Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать
Частные случаи
Неоднородность в виде многочлена
Теперь рассмотрим некоторые более простые виды специальной неоднородности. Начнем с неоднородной части в виде многочлена:
,
где – многочлен степени s . Этот случай принадлежит к общему виду специальной неоднородности (2), в котором . Основываясь на вышеизложенном, получаем следующие правила составления вида частного решения.
Если среди корней характеристического уравнения (4) нет нулевого корня
,
то частное решение имеет вид:
.
То есть оно является многочленом степени s с неопределенными коэффициентами .
Если характеристическое уравнение (4) имеет нулевой корень кратности p :
,
то частное решение имеет вид:
.
Неоднородность в виде произведения экспоненты и многочлена
Теперь рассмотрим неоднородную часть в виде произведения многочлена степени s и экспоненты:
.
Этот случай принадлежит к общему виду (2), в котором .
Если среди корней характеристического уравнения нет действительного корня со значением α :
,
то частное решение является произведением многочлена степени s и экспоненты:
.
Если характеристическое уравнение (4) имеет действительный корень α кратности p :
,
то частное решение имеет вид:
.
Неоднородность в виде суммы произведений многочленов на косинус и синус
Наконец рассмотрим неоднородную часть в виде суммы произведений многочленов степеней на косинус и синус:
.
Этот случай принадлежит к общему виду (2), в котором .
Если среди корней характеристического уравнения нет чисто мнимого корня со значением iβ :
,
то частное решение является суммой произведений многочленов, косинуса и синуса:
,
где – наибольшее из и .
,
– многочлены степени s с неизвестными коэффициентами .
Если характеристическое уравнение (4) имеет чисто мнимый корень iβ кратности p :
,
то частное решение имеет вид:
.
То есть частное решение как и в предыдущем случае, но умноженное на .
Автор: Олег Одинцов . Опубликовано: 30-07-2013 Изменено: 14-09-2020
Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать
Линейные уравнения первого порядка
Назначение сервиса . Онлайн калькулятор можно использовать для проверки решения однородных и неоднородных линейных дифференциальных уравнений вида y’+y=b(x) .
- Решение онлайн
- Видеоинструкция
Теорема. Пусть a1(x) , a0(x) , b(x) непрерывны на отрезке [α,β], a1≠0 для ∀x∈[α,β]. Тогда для любой точки (x0, y0), x0∈[α,β], существует единственное решение уравнения, удовлетворяющее условию y(x0) = y0 и определенное на всем интервале [α,β].
Рассмотрим однородное линейное дифференциальное уравнение a1(x)y’+a0(x)y=0 .
Разделяя переменные, получаем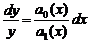 
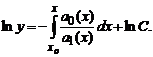
, или, интегрируя обе части, 
Последнее соотношение, с учетом обозначения exp(x) = e x , записывается в форме
Попытаемся теперь найти решение уравнения в указанном виде, в котором вместо константы C подставлена функция C(x) то есть в виде
Подставив это решение в исходное, после необходимых преобразований получаем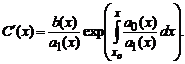 
Интегрируя последнее, имеем
где C1— некоторая новая константа. Подставляя полученное выражение для C(x), окончательно получаем решение исходного линейного уравнения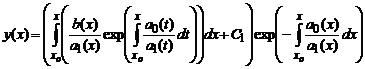 
.
Описанный метод решения называется методом Лагранжа или методом вариации произвольной постоянной (см. также Метод вариации произвольной постоянной решения линейных неоднородных уравнений).
Пример . Решить уравнение y’ + 2y = 4x . Рассмотрим соответствующее однородное уравнение y’ + 2y = 0 . Решая его, получаем y = Ce -2 x . Ищем теперь решение исходного уравнения в виде y = C(x)e -2 x . Подставляя y и y’ = C'(x)e -2 x — 2C(x)e -2 x в исходное уравнение, имеем C'(x) = 4xe 2 x , откуда C(x) = 2xe 2 x — e 2 x + C1 и y(x) = (2xe 2 x — e 2 x + C1)e -2 x = 2x — 1 + C1e -2 x — общее решение исходного уравнения. В этом решении y1(x) = 2x-1 — движение объекта под действием силы b(x) = 4x, y2(x) = C1e -2 x -собственное движение объекта.
Пример №2 . Найти общее решение дифференциального уравнения первого порядка y’+3 y tan(3x)=2 cos(3x)/sin 2 2x.
Это неоднородное уравнение. Сделаем замену переменных: y=u•v, y’ = u’v + uv’.
3u v tg(3x)+u v’+u’ v = 2cos(3x)/sin 2 2x или u(3v tg(3x)+v’) + u’ v= 2cos(3x)/sin 2 2x
Решение состоит из двух этапов:
1. u(3v tg(3x)+v’) = 0
2. u’v = 2cos(3x)/sin 2 2x
1. Приравниваем u=0, находим решение для 3v tg(3x)+v’ = 0
Представим в виде: v’ = -3v tg(3x)
Интегирируя, получаем:
ln(v) = ln(cos(3x))
v = cos(3x)
2. Зная v, Находим u из условия: u’v = 2cos(3x)/sin 2 2x
u’ cos(3x) = 2cos(3x)/sin 2 2x
u’ = 2/sin 2 2x
Интегирируя, получаем: 
Из условия y=u•v, получаем:
y = u•v = (C-cos(2x)/sin(2x)) cos(3x) или y = C cos(3x)-cos(2x) ctg(3x)
🎥 Видео
Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать
Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать
13. Как решить дифференциальное уравнение первого порядка?Скачать
Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать
Дифференциальные уравнения, 9 урок, Линейные дифференциальные уравнения высших порядковСкачать
ЛОДУ 2 порядка c постоянными коэффициентамиСкачать
9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать
Спецкурс по диффурам 10 (17.11.23) — ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И МАТРИЧНАЯ ЭКСПОНЕНТАСкачать
10. Уравнения БернуллиСкачать
Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать
Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
