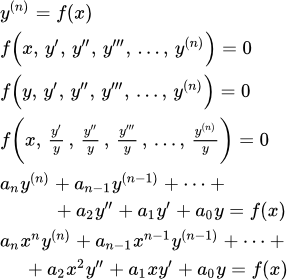Линейные дифференциальные уравнения четвертого порядка

Можно выделить 5 возможных метода для определения y₀ — общего решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами:

1. В случае, когда все решения характеристического уравнения являются действительными и различными, значит, линейно независимые частные решения принимают вид:

,

а общее решение линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами записывают так:

.

Найти общее решение ЛОДУ 3-го порядка с постоянными коэффициентами:

.

Для начала записываем характеристическое уравнение и находим его корни, перед этим произведя разложение многочлена в левой части равенства на множители методом группировки:

Каждый из трех корней характеристического уравнения являются действительными и различными, значит, общее решение линейного однородного дифференциального уравнения 3-го порядка с постоянными коэффициентами принимает вид:

.

2. Когда каждое решение характеристического уравнения оказывается действительными и одинаковыми, т.е.,

,

значит, линейно независимые частные решения ЛОДУ n-ого порядка с постоянными коэффициентами принимают вид:

,

а общее решение линейного однородного дифференциального уравнения (ДУ) принимает вид:

Найти общее решение ДУ

.

Характеристическое уравнение этого линейного однородного дифференциального уравнения 4-го порядка выглядит так:

.

Обратившись к формуле бинома Ньютона, переписываем характеристическое уравнение как , из чего видим четырехкратный корень k₀ = 2.

Т.о., общим решением заданного ЛОДУ с постоянными коэффициентами является:

.

3. Когда решениями характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами оказываются разные комплексно сопряженные пары , n=2m, тогда линейно независимые частные решения такого линейного однородного дифференциального уравнения принимает вид:

а общее решение записывается так:

Проинтегрировать ЛОДУ 4-го порядка с постоянными коэффициентами .

Характеристическое уравнение этого линейного однородного дифференциального уравнения:

.

Произведя некоторые несложные преобразования и группирования имеем:

Откуда находим 2 пары комплексно сопряженных корней характеристического уравнения и . Тогда, общим решением заданного ЛОДУ n-ого порядка с постоянными коэффициентами является:

4. Когда решениями характеристического уравнения оказываются совпадающие комплексно сопряженные пары , тогда линейно независимые частные решения ЛОДУ n-ого порядка с постоянными коэффициентами выглядят так:

,

а общим решением этого линейного однородного дифференциального уравнения является:

Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами:

.

Первым шагом записываем характеристическое уравнение этого ЛОДУ с постоянными коэффициентами и определяем его корни:

Т.е., решением характеристического уравнения является двукратная комплексно сопряженная пара . Тогда общее решение заданного ЛОДУ с постоянными коэффициентами будет:

.

5. Могут возникнуть любые комбинации случаев, описанных выше, т.е., некоторые корни характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами являются действительными и различными, некоторые являются действительными и совпадающими, некоторые являются различными комплексно сопряженными парами и некоторые совпадающими комплексно сопряженными парами.

Найти общее решение ДУ

.

Характеристическое уравнение этого ЛОДУ с постоянными коэффициентами выглядит так:

.

Многочлен в левой части равенства можно разложить на множители. Из делителей свободного члена вычисляем двукратный корень k₁=k₂=2 и корень k₃=-3. Далее, применяя схему Горнера, приходим к разложению:

.

Из квадратного уравнения находим оставшиеся корни .

Т.о., общее решение заданного ЛОДУ с постоянными коэффициентами выглядит как:

.

Видео:Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами

Ниже разберем способы, как решить линейные однородные и неоднородные дифференциальные уравнения порядка выше второго, имеющих постоянные коэффициенты. Подобные уравнения представлены записями y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , в которых f 0 , f 1 , . . . , f n — 1 — являются действительными числами, а функция f ( x ) является непрерывной на интервале интегрирования X .

Оговоримся, что аналитическое решение подобных уравнений иногда неосуществимо, тогда используются приближенные методы. Но, конечно, некоторые случаи дают возможность определить общее решение.

Видео:Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Общее решение ЛОДУ и ЛДНУ

Мы зададим формулировку двух теорем, показывающих, какого вида общих решений ЛОДУ и ЛНДУ n -ого порядка следует искать.

Общим решением y 0 ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 на интервале
X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) будет линейная комбинация
n линейно независимых частных решений ЛОДУ y j , j = 1 , 2 , . . . , n , содержащая произвольные постоянные коэффициенты C j , j = 1 , 2 , . . . , n , то есть y 0 = ∑ j = 1 n C j · y j .

Общим решением y ЛНДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) на интервале X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) и функцией f ( x ) будет являться сумма y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 , а y

— некоторое частное решение исходного ЛНДУ.

Итак, общее решение линейного неоднородного дифференциального уравнения, содержащего постоянные коэффициенты y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , нужно искать, как y = y 0 + y

— некоторое его частное решение, а y 0 = ∑ j = 1 n C j · y j – общее решение соответствующего однородного дифференциального уравнения y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

В первую очередь рассмотрим, как осуществлять нахождение y 0 = ∑ j = 1 n C j · y j — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами, а потом научимся определять частное решение y

линейного неоднородного дифференциального уравнения n -ого порядка при постоянных коэффициентах.

Алгебраическое уравнение n -ого порядка k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 носит название характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка, содержащего постоянные коэффициенты, записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

Возможно определить n частных линейно независимых решений y 1 , y 2 , . . . , y n исходного ЛОДУ, исходя из значений найденных n корней характеристического уравнения k 1 , k 2 , . . . , k n .

Видео:Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Методы решения ЛОДУ и ЛНДУ

Укажем все существующие варианты и приведем примеры на каждый.

1. Когда все решения k 1 , k 2 , . . . , k n характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 действительны и различны, линейно независимые частные решения будут выглядеть так:
   y 1 = e k 1 · x , y 2 = e k 2 · x , . . . , y n = e k n · x . Общее же решение ЛОДУ n -ого порядка при постоянных коэффициентах запишем как: y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x + . . . + C n · e k n · x .

Пример 1

Задано ЛОДУ третьего порядка, содержащее постоянные коэффициенты y ‘ ‘ ‘ — 3 y » — y ‘ + 3 y = 0 . Определите его общее решение.

Решение

Cоставим характеристическое уравнение и найдем его корни, разложив предварительно многочлен из левой части равенства на множители, используя метод группировки:
k 3 — 3 k 2 — k + 3 = 0 k 2 ( k — 3 ) — ( k — 3 ) = 0 ( k 2 — 1 ) ( k — 3 ) = 0 k 1 = — 1 , k 2 = 1 , k 3 = 3

Ответ: найденные корни являются действительными и различными, значит общее решение ЛОДУ третьего порядка с постоянными коэффициентами запишем как: y 0 = C 1 · e — x + C 2 e x + C 3 · e 3 x .

1. Когда решения характеристического уравнения являются действительными и одинаковыми ( k 1 = k 2 = . . . = k n = k 0 ) , линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами буду иметь вид: y 1 = e k 0 · x , y 2 = x · e k 0 · x , . . . , y n = x n — 1 · e k 0 · x .

Общее же решение ЛОДУ будет выглядеть так:
y 0 = C 1 · e k 0 · x + C 2 · e k 0 · x + . . . + C n · x n — 1 · e k 0 · x = = e k 0 · x · C 1 + C 2 · x + . . . + C n · x n — 1

Задано дифференциальное уравнение: y ( 4 ) — 8 k ( 3 ) + 24 y » — 32 y ‘ + 16 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 8 k 3 + 24 k 2 — 32 k + 16 = 0 .

Преобразуем данное характеристическое уравнение, используя формулу бинома Ньютона, оно примет вид: k — 2 4 = 0 . Отсюда мы выделим его четырехкратный корень k 0 = 2 .

Ответ: общим решением заданного ЛОДУ станет: y 0 = e 2 x · C 1 + C 2 · x + C 3 · x 2 + C 4 · x 3

1. Когда решения характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка при постоянных коэффициентах — различные комплексно сопряженные пары α 1 ± i · β 1 , α 2 ± i · β 2 , . . . , α m ± i · β m , n = 2 m , линейно независимые частные решения такого ЛОДУ будут иметь вид:
   y 1 = e α 1 x · cos β 1 x , y 2 = e α 1 x · sin β 1 x , y 3 = e α 2 x · cos β 2 x , y 4 = e α 2 x · sin β 2 x , … y n — 1 = e α m x · cos β m x , y n = e α m x · sin β m x

Общее же решение запишем так:

y 0 = e α 1 x · C 1 · cos β 1 x + C 2 · sin β 1 x + + e α 2 x · C 3 · cos β 2 x + C 4 · sin β 2 x + . . . + + e α m x · C n — 1 · cos β m x + C n · sin β m x

Задано ЛОДУ четвертого порядка при постоянных коэффициентах y ( 4 ) — 6 y ( 3 ) + 14 y » — 6 y ‘ + 13 y = 0 . Необходимо его проинтегрировать.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 . Осуществим преобразования и группировки:

k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 k 4 + k 2 — 6 k 3 + k + 13 k 2 + 1 = 0 k 2 + 1 k 2 — 6 k + 13 = 0

Из полученного результата несложно записать две пары комплексно сопряженных корней k 1 , 2 = ± i и k 3 , 4 = 3 ± 2 · i .

Ответ: общее решение заданного линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами запишется как:
y 0 = e 0 · C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x = = C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x

1. Когда решения характеристического уравнения — это совпадающие комплексно сопряженные пары α ± i · β , линейно независимыми частными решениями линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами будут записи:
   y 1 = e α · x · cos β x , y 2 = e α · x · sin β x , y 3 = e α · x · x · cos β x , y 4 = e α · x · x · sin β x , … y n — 1 = e α · x · x m — 1 · cos β x , y n = e α · x · x m — 1 · sin β x

Общим решением ЛОДУ будет:

y 0 = e α · x · C 1 · cos β x + C 2 · sin β x + + e α · x · x · C 4 · cos β x + C 3 · sin β x + . . . + + e α · x · x m — 1 · C n — 1 · cos β x + C n · sin β x = = e α · x · cos β x · C 1 + C 3 · x + . . . + C n — 1 · x m — 1 + + e α · x · sin β x · C 2 + C 4 · x + . . . + C n · x m — 1

Задано линейное однородное дифференциальное уравнение с постоянными коэффициентами y ( 4 ) — 4 y ( 3 ) + 14 y » — 20 y ‘ + 25 y = 0 . Необходимо определить его общее решение.

Решение

Составим запись характеристического уравнения, заданного ЛОДУ, и определим его корни:

k 4 — 4 k 3 + 14 k 2 — 20 k + 25 = 0 k 4 — 4 k 3 + 4 k 2 + 10 k 2 — 20 k + 25 = 0 ( k 2 — 2 k ) 2 + 10 ( k 2 — 2 k ) + 25 = 0 ( k 2 — 2 k + 5 ) 2 = 0 D = — 2 2 — 4 · 1 · 5 = — 16 k 1 , 2 = k 3 , 4 = 2 ± — 16 2 = 1 ± 2 · i

Таким образом, решением характеристического уравнения будет двукратная комплексно сопряженная пара α ± β · i = 1 ± 2 · i .

Ответ: общее решение заданного ЛОДУ: y 0 = e x · cos 2 x · ( C 1 + C 3 · x ) + e x · sin 2 x · ( C 2 + C 4 · x )

1. Встречаются различные комбинации указанных случаев: некоторые корни характеристического уравнения ЛОДУ n -ого порядка с постоянными коэффициентами являются действительными и различными, некоторые — действительными и совпадающими, а какие-то — комплексно сопряженными парами или совпадающими комплексно сопряженными парами.

Пример 5

Задано дифференциальное уравнение y ( 5 ) — 9 y ( 4 ) + 41 ( 3 ) + 35 y » — 424 y ‘ + 492 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = 0 .

Левая часть содержит многочлен, который возможно разложить на множители. В числе делителей свободного члена определяем двукратный корень k 1 = k 2 = 2 и корень k 3 = — 3 .

На основе схемы Горнера получим разложение: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = k + 3 k — 2 2 k 2 — 8 k + 41 .

Квадратное уравнение k 2 — 8 k + 41 = 0 дает нам оставшиеся корни k 4 , 5 = 4 ± 5 · i .

Ответ: общим решением заданного ЛОДУ с постоянными коэффициентами будет: y 0 = e 2 x · C 1 + C 2 x + C 3 · e — 3 x + e 4 x · C 4 · cos 5 x + C 5 · sin 5 x

Таким образом, мы рассмотрели основные случаи, когда возможно определить y 0 — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами.

Следующее, что мы разберем – это ответ на вопрос, как решить линейное неоднородное дифференциальное уравнение n -ого порядка с постоянными коэффициентами записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) .

Общее решение в таком случае составляется как сумма общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ: y = y 0 + y

. Поскольку мы уже умеем определять y 0 , остается разобраться с нахождением y

, т.е. частного решения ЛНДУ порядка n с постоянными коэффициентами.

Приведем все способы нахождения y

согласно тому, какой вид имеет функция f ( x ) , находящаяся в правой части рассматриваемого ЛНДУ.

Когда f ( x ) представлена в виде многочлена n -ой степени f ( x ) = P n ( x ) , частным решением ЛНДУ станет: y

= Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом степени n , а r – указывает, сколько корней характеристического уравнения равно нулю.
Когда функция f ( x ) представлена в виде произведения многочлена степени n и экспоненты f ( x ) = P n ( x ) · e α · x , частным решением ЛНДУ второго порядка станет: y

= e α · x · Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом n —ой степени, r указывает, сколько корней характеристического уравнения равно α .
Когда функция f ( x ) записана как f ( x ) = A 1 cos ( β x ) + B 1 sin ( β x ) , где А 1 и В 1 – числа, частным решением ЛНДУ станет запись y

= A cos β x + B sin β x · x γ . Здесь где А и В являются неопределенными коэффициентами, r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно ± i β .
Когда f ( x ) = e α x · P n ( x ) sin β x + Q k x cos β x , то y

= e α x · L m x sin β x + N m x cos β x · x γ , где r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно α ± i β , P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , m и m соответственно, m = m a x ( n , k ) .

Коэффициенты, которые неизвестны, определяются из равенства y

( n — 1 ) + . . . + f 1 y

Подробности нахождения решений уравнений в каждом из указанных случаев можно изучить в статье линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, поскольку схемы решения ЛНДУ степени выше второй полностью совпадают.

Когда функция f ( x ) имеет любой иной вид, общее решение ЛНДУ возможно определить, используя метод вариации произвольных постоянных. Его разберем подробнее.

Пусть нам заданы y j , j = 1 , 2 , . . . , n — n линейно независимые частные решения соответствующего ЛОДУ, тогда, используя различные вариации произвольных постоянных, общим решением ЛНДУ
n -ого порядка с постоянными коэффициентами будет запись: н = ∑ j = 1 n C j ( x ) · y j . В нахождении производных функций C j ( x ) , j = 1 , 2 , . . . , n поможет система уравнений:

∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0

а собственно функции C j ( x ) , j = 1 , 2 , . . . , n найдем при последующем интегрировании.

Задано ЛНДУ с постоянными коэффициентами: y ‘ ‘ ‘ — 5 y » + 6 y ‘ = 2 x . Необходимо найти его общее решение.

Решение

Составим характеристическое уравнение: k 3 — 5 k 2 + 6 k = 0 . Корни данного уравнения: k 1 = 0 , k 2 = 2 и k 3 = 3 . Таким образом, общим решением ЛОДУ будет запись: y 0 = C 1 + C 2 · e 2 x + C 3 · e 3 x , а частные линейно независимые решения это: y 1 = 1 , y 2 = e 2 x , y 3 = e 3 x .

Варьируем произвольные постоянные: y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x .

Чтобы определить C 1 ( x ) , C 2 ( x ) и C 3 ( x ) , составим систему уравнений:

C ‘ 1 ( x ) · y 1 + C ‘ 2 ( x ) · y 2 + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · y ‘ 1 + C ‘ 2 ( x ) · y ‘ 2 + C ‘ 3 ( x ) · y ‘ 3 = 0 C ‘ 1 ( x ) · y » 1 + C ‘ 2 ( x ) · y » 2 + C ‘ 3 ( x ) · y » 3 = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · 1 ‘ + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · e 3 x ‘ = 0 C ‘ 1 ( x ) · 1 ‘ ‘ + C ‘ 2 x · e 2 x ‘ ‘ + C ‘ 3 ( x ) · e 3 x ‘ ‘ = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x + C ‘ 3 ( x ) · e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 2 e 2 x + C ‘ 3 ( x ) · 3 e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 4 e 2 x + C ‘ 3 ( x ) · 9 e 3 x = 2 x

Решаем, используя метод Крамера:

∆ = 1 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 0 4 e 2 x 9 e 3 x = 18 e 2 x · e 3 x — 12 e 2 x · e 3 x = 6 e 5 x ∆ C 1 ‘ ( x ) = 0 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 2 x 4 e 2 x 9 e 3 x = e 5 x · 2 x ⇒ C ‘ 1 ( x ) = ∆ C 1 ‘ ( x ) ∆ = e 5 x · 2 x 6 e 5 x = 1 6 · 2 x ∆ C 2 ‘ ( x ) = 1 0 e 3 x 0 0 3 e 3 x 0 2 x 9 e 3 x = — 3 e x · 2 x ⇒ C ‘ 2 ( x ) = ∆ C 2 ‘ ( x ) ∆ = — 3 e 3 x · 2 x 6 e 5 x = — 1 2 · e — 2 x · 2 x ∆ C 3 ‘ ( x ) = 1 e 2 x 0 0 2 e 2 x 0 0 4 e 2 x 2 x = 2 e 2 x · 2 x ⇒ C ‘ 3 ( x ) = ∆ C 3 ‘ ( x ) ∆ = 2 e 2 x · 2 x 6 e 5 x = 1 3 · e — 3 x · 2 x

Интегрируем C ‘ 1 ( x ) = 1 6 · 2 x с помощью таблицы первообразных, а
C ‘ 2 ( x ) = — 1 2 · e — 2 x · 2 x и C ‘ 3 ( x ) = 1 3 · e — 3 x · 2 x при помощи метода интегрирования по частям, получим:
C 1 ( x ) = 1 6 · ∫ 2 x d x = 1 6 · 2 x ln 2 + C 4 C 2 ( x ) = — 1 2 · ∫ e — 2 x · 2 x d x = — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 C 3 ( x ) = 1 3 · ∫ e — 3 x · 2 x d x = 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6

Ответ: искомым общим решением заданного ЛОДУ с постоянными коэффициентами будет:

y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x = = 1 6 · 2 x ln 2 + C 4 + — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 · e 2 x + + 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6 · e 3 x

где C 4 , C 5 и C 6 – произвольные постоянные.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения высших порядков

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Уравнения, содержащие переменную и старшую производную

Разрешенные относительно старшей производной

Рассмотрим дифференциальное уравнение следующего вида:
.
Интегрируем n раз.
;
;
и так далее. Так же можно использовать формулу:
.
См. Дифференциальные уравнения, решающиеся непосредственным интегрированием

Разрешенные относительно переменной

Рассмотрим дифференциальное уравнение, в котором независимая переменная x является функцией от старшей производной:
.
Это уравнение можно решить параметрическим методом. Для этого вводим параметр . В результате получаем:
;
.
Из последнего уравнения . Интегрируя, получаем зависимость производной от x в параметрическом виде:
.
Продолжая интегрирование аналогичным образом, получим зависимость y от x в параметрическом виде.

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только независимую переменную и старшую производную общего вида:
.
Его можно решить в квадратурах в параметрическом виде, если удастся подобрать такие функции и , для которых .

Если такие функции найдены, то положим . Тогда исходное уравнение выполняется автоматически. Дифференцируя первую функцию, находим связь между дифференциалами переменных x и t : . Тогда
.
Интегрируя последнее соотношение, получаем решение для производной более низкого порядка в параметрическом виде. Продолжая действовать подобным способом, получим общее решение в квадратурах.

Уравнения, содержащие только производные порядков n и n-1

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Тогда положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению .

Тогда
;
.
Интегрируя эти уравнения, получим параметрическое представление производной порядка n – 2 . Продолжая подобным образом, получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Уравнения, содержащие только производные порядков n и n-2

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению.

Тогда
;
;
;
;
.
Интегрируя, получим параметрическое представление производных порядка n, n – 1 и n – 2 . Далее интегрируем как в предыдущем случае ⇑. В результате получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Видео:Дифференциальные уравнения, 9 урок, Линейные дифференциальные уравнения высших порядковСкачать

Дифференциальные уравнения высших порядков, допускающие понижение порядка

Уравнения, не содержащие зависимую переменную y в явном виде

Подстановка приводит к понижению порядка уравнения на единицу. Здесь – функция от .
См. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде

Уравнения, не содержащие независимую переменную x в явном виде

Для решения этого уравнения, делаем подстановку
.
Считаем, что является функцией от . Тогда
.
Аналогично для остальных производных. В результате порядок уравнения понижается на единицу.
См. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде

Однородные дифференциальные уравнения высших порядков

Уравнения, однородные относительно функции и ее производных

Дифференциальное уравнение

является однородным относительно функции и ее производных, если оно обладает свойством:
.
Здесь t – число или любая функция; число p называют показателем однородности.

Чтобы распознать такое уравнение, нужно сделать замену
.
Если после преобразований t сократится, то это однородное уравнение.

Для его решения делаем подстановку
,
где – функция от . Тогда
.
Аналогично преобразуем производные и т.д. В результате порядок уравнения понижается на единицу.
См. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков

Обобщенно однородные уравнения относительно переменных

Теперь рассмотрим дифференциальные уравнения, которые не меняют вида, если сделать замену переменных: , где c – постоянная; s – измерение однородности для переменной y. При такой замене производная порядка m умножается на :
.
Если записать исходное уравнение в общем виде:
,
то оно является обобщенно однородным относительно переменных, если обладает свойством:
,
где t – число или любая функция; p – показатель однородности.

При подобные уравнения можно назвать однородными дифференциальными уравнениями относительно переменных.

Порядок такого уравнения можно понизить на единицу, если искать решение в параметрическом виде, и перейти от зависимой переменной (функции) y к новой зависимой переменной (новой функции) с помощью подстановок:
, где t – параметр.
В результате для функции получим дифференциальное уравнение n — го порядка, которое не содержит переменную t в явном виде. Далее понижаем порядок изложенным выше методом ⇑.
См. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков

Дифференциальные уравнения с полной производной

Это уравнения, которые можно привести к полной производной:
.
Отсюда сразу получаем первый интеграл:
.
Он представляет собой дифференциальное уравнение, на единицу меньшего порядка по сравнению с исходным уравнением .

В качестве примера рассмотрим дифференциальное уравнение второго порядка:
.
Разделим его на . Тогда
.
Отсюда получаем первый интеграл, который является дифференциальным уравнением первого порядка:
.
См. Дифференциальные уравнения высших порядков с полной производной.

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Линейные дифференциальные уравнения высших порядков

Рассмотрим линейное однородное дифференциальное уравнение n-го порядка:
(1) ,
где – функции от независимой переменной . Пусть есть n линейно независимых решений этого уравнения. Тогда общее решение уравнения (1) имеет вид:
(2) ,
где – произвольные постоянные. Сами функции образуют фундаментальную систему решений.
Фундаментальная система решений линейного однородного уравнения n-го порядка – это n линейно независимых решений этого уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка:
.
Пусть есть частное (любое) решение этого уравнения. Тогда общее решение имеет вид:
,
где – общее решение однородного уравнения (1).

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Линейные дифференциальные уравнения с постоянными коэффициентами и приводящиеся к ним

Линейные однородные уравнения с постоянными коэффициентами

Это уравнения вида:
(3) .
Здесь – действительные числа. Чтобы найти общее решение этого уравнения, нам нужно найти n линейно независимых решений , которые образуют фундаментальную систему решений. Тогда общее решение определяется по формуле (2):
(2) .

Ищем решение в виде . Получаем характеристическое уравнение:
(4) .

Если это уравнение имеет различные корни , то фундаментальная система решений имеет вид:
.

Если имеется комплексный корень
,
то существует и комплексно сопряженный корень . Этим двум корням соответствуют решения и , которые включаем в фундаментальную систему вместо комплексных решений и .

Кратным корням кратности соответствуют линейно независимых решений: .

Кратным комплексным корням кратности и их комплексно сопряженным значениям соответствуют линейно независимых решений:
.

Линейные неоднородные уравнения со специальной неоднородной частью

Рассмотрим уравнение вида
,
где – многочлены степеней s 1 и s 2 ; – постоянные.

Сначала мы ищем общее решение однородного уравнения (3). Если характеристическое уравнение (4) не содержит корень , то ищем частное решение в виде:
,
где
;
;
s – наибольшее из s 1 и s 2 .

Если характеристическое уравнение (4) имеет корень кратности , то ищем частное решение в виде:
.

После этого получаем общее решение:
.

Линейные неоднородные уравнения с постоянными коэффициентами

Здесь возможны три способа решения.

1) Метод Бернулли.
Сначала находим любое, отличное от нуля, решение однородного уравнения
.
Затем делаем подстановку
,
где – функция от переменной x . Получаем дифференциальное уравнение для u , которое содержит только производные от u по x . Выполняя подстановку , получаем уравнение n – 1 — го порядка.

2) Метод линейной подстановки.
Сделаем подстановку
,
где – один из корней характеристического уравнения (4). В результате получим линейное неоднородное уравнение с постоянными коэффициентами порядка . Последовательно применяя такую подстановку, приведем исходное уравнение к уравнению первого порядка.

3) Метод вариации постоянных Лагранжа.
В этом методе мы сначала решаем однородное уравнение (3). Его решение имеет вид:
(2) .
Далее мы считаем, что постоянные являются функциями от переменной x . Тогда решение исходного уравнения имеет вид:
,
где – неизвестные функции. Подставляя в исходное уравнение и накладывая на некоторые ограничения, получаем уравнения, из которых можно найти вид функций .

Уравнение Эйлера

Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
.
Однако, для решения уравнения Эйлера, делать такую подстановку нет необходимости. Можно сразу искать решение однородного уравнения в виде
.
В результате получим такие же правила, как и для уравнения с постоянными коэффициентами, в которых вместо переменной нужно подставить .

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 13-06-2017 Изменено: 11-05-2021

🎥 Видео

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Видеоурок "Линейные однородные диф. уравнения n-го порядка"Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

Операционное исчисление. Решение дифференциального уравнения четвертого порядка.Скачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать