Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.
- Определение понятия регрессии
- Какие бывают типы связей между переменными
- Виды регрессий
- Гиперболическая, линейная и логарифмическая
- Множественная и нелинейная
- Обратные и парные виды регрессий
- Понятие корреляции
- Методы
- Корреляция для множественной регрессии
- Метод наименьших квадратов
- Параметры уравнений
- Сгруппированные данные
- Множественное парное уравнение регрессии: оценка важности связи
- Какие факторы необходимо учитывать при построении множественной регрессии
- Методы построения
- Методы многомерного анализа
- Оценка параметров линейных уравнений регрессии
- Множественная регрессия
- Множественная линейная регрессия в скалярной и векторной формах
- Метод наименьших квадратов и предпосылки его применения для множественной линейной регрессии
Видео:Множественная регрессияСкачать

Определение понятия регрессии
В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).
Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

Какие бывают типы связей между переменными
В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.
Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.
Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.
Видео:Множественная регрессия в ExcelСкачать

Виды регрессий
На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Гиперболическая, линейная и логарифмическая
Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.
Видео:Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Множественная и нелинейная
Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х1 , х2 . хс)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.
Видео:Парная регрессия: линейная зависимостьСкачать

Обратные и парные виды регрессий
Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.
Видео:Выбор факторов, влияющих на результативный показательСкачать

Понятие корреляции
Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.
Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать

Методы
Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.
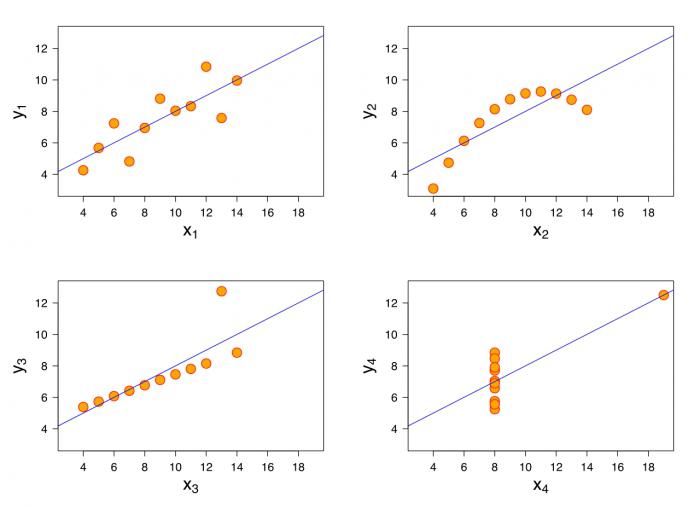
Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.
В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.
Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).
Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Корреляция для множественной регрессии
Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.
Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.
Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Метод наименьших квадратов
Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.
Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.
Видео:Эконометрика. Линейная парная регрессияСкачать

Параметры уравнений
Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.
Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.
Видео:Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Сгруппированные данные
Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.
Видео:Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Множественное парное уравнение регрессии: оценка важности связи
Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x1,x2,…,xm)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.
Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.
Линейная функция изображается в форме такой взаимосвязи: у = а0 + a1х1 + а2х2,+ . + amxm. При этом а2, am, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.
Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах1 b1 х2 b2 . xm bm . В данном случае показатели b1, b2. bm – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.
Видео:Уравнение множественной регрессии в ExcelСкачать

Какие факторы необходимо учитывать при построении множественной регрессии
Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.
Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:
- Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
- Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
- В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Методы построения
Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:
- Способ исключения.
- Способ включения.
- Пошаговый анализ регрессии.
Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.
Видео:09 Множественная регрессияСкачать

Методы многомерного анализа
Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.
Видео:РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать

Оценка параметров линейных уравнений регрессии
Спецификация модели
+наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов
-раздел экономической теории, связанный с анализом статистической информации
-специальный раздел математики, посвященный анализу экономической информации
-наука, которая осуществляет качественный анализ взаимосвязей экономических явлений и процессов
#Основной задачей эконометрики является…
+исследование взаимосвязей экономических явлений и процессов
-отражение особенностей социального развития общества
-установление связей между различными процессами в обществе и технических процессом
— анализ технического прогресса на примере социально–экономических показателей
#При выборе спецификации модели парная регрессия используется в случае, когда …
+среди множества факторов, влияющих на результат можно выделить доминирующий фактор
-среди множества факторов, влияющих на результат нельзя выделить доминирующий фактор
-среди множества факторов, влияющих на результат можно выделить несколько факторов
-среди множества факторов, влияющих на результат можно выделить лишь случайные факторы
#Объем выборки должен превышать число рассчитываемых параметров при исследуемых факторах …
#К ошибкам спецификации относится …
+неправильный выбор той или иной математической функции
-однородность выбранной совокупности
-учет в модели случайных факторов
— учет в модели существенных факторов
#Относительно формы зависимости различают …
+линейную и нелинейную регрессии
-простую и множественную регрессии
-непосредственную и косвенную регрессии
-положительную и отрицательную регрессии
#Относительно количества факторов, включенных в уравнение регрессии различают …
+простую и множественную регрессии
-линейную и нелинейную регрессии
-непосредственную и косвенную регрессии
— множественную и многофакторную регрессии
#Простая линейная регрессия предполагает …
+наличие одного фактора и линейность уравнения регрессии
-наличие двух и более факторов и линейность уравнения регрессии
-наличие одного фактора и нелинейность уравнения регрессии
-наличие двух и более факторов и нелинейность уравнения регрессии
#Объем выборки определяется …
+числом параметров при независимых переменных
-числом результативных переменных
-объемом генеральной совокупности
-числовыми значениями переменных отбираемых в выборку
#Дано уравнение регрессии 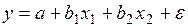
+линейное уравнение множественной регрессии
-линейное уравнение простой регрессии
-полиномиальное уравнение множественной регрессии
— полиномиальное уравнение парной регрессии
#Выбор формы зависимости экономических показателей и определение количества факторов в модели называется _____________ эконометрической модели.
#Коэффициент парной корреляции характеризует …
+тесноту линейной связи между двумя переменными
-тесноту нелинейной связи между двумя переменными
-тесноту линейной связи между несколькими переменными
-тесноту нелинейной связи между несколькими переменными
#Мультиколлинеарность факторов эконометрической модели подразумевает …
+наличие линейной зависимости между более чем двумя факторами
-наличие линейной зависимости между двумя факторами
-отсутствие зависимости между факторами
-наличие нелинейной зависимости между двумя факторами
#Взаимодействие факторов эконометрической модели означает, что …
+факторы дублируют влияние друг друга на результат
-влияние одного из факторов на результирующий признак не зависит от значений другого фактора
-влияние факторов на результирующий признак усиливается, начиная с определенного уровня значений факторов
— влияние факторов на результирующий признак зависит от значений другого неколлинеарного им фактора
#Отбор факторов в модель множественной регрессии при помощи метода включения основан на сравнении значений …
+остаточной дисперсии до и после включения фактора в модель
-общей дисперсии до и после включения фактора в модель
-дисперсии до и после включения результата в модель
-остаточной дисперсии до и после включения случайных факторов в модель
#Величина остаточной дисперсии при включении существенного фактора в модель …
— будет равна нулю
#В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между …
-параметрами и переменными
-переменными и случайными факторами
#Матрица парных коэффициентов корреляции строится для выявления коллинеарных и мультиколлинеарных …
#Факторы эконометрической модели являются коллинеарными, если коэффициент …
+корреляции между ними по модулю больше 0,7
-детерминации между ними по модулю больше 0,7
-корреляции между ними по модулю меньше 0,7
-детерминации между ними по модулю меньше 0,7
#Из пары коллинеарных факторов в эконометрическую модель включается тот фактор …
+который при достаточно тесной связи с результатом имеет меньшую связь с другими факторами
-который при который при отсутствии связи с результатом имеет меньшую связь с другими факторами
-который при отсутствии связи с результатом имеет максимальную связь с другими факторами
-который при достаточно тесной связи с результатом имеет наибольшую связь с другими факторами
#Величина коэффициента детерминации при включении существенного фактора в эконометрическую модель …
-существенно не изменится
— будет равна нулю
#Основным требованием к факторам, включаемым в модель множественной регрессии, является …
+отсутствие взаимосвязи между факторами
-наличие тесной взаимосвязи между факторами
-отсутствие взаимосвязи между результатом и фактором
-отсутствие линейной взаимосвязи между факторами
#Фиктивными переменными в уравнении множественной регрессии являются …
+качественные переменные, преобразованные в количественные
-дополнительные количественные переменные, улучшающие решение
-комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели
-переменные, представляющие простейшие функции от уже включенных в модель переменных
#В качестве фиктивных переменных в модель множественной регрессии включаются факторы, …
+не имеющие количественных значений
-имеющие количественные значения
-не имеющие качественных значений
— имеющие вероятностные значения
#При включении фиктивных переменных в модель им присваиваются …
#Исходные значения фиктивных переменных предполагают значения …
#Проводится исследование зависимости выработки работника предприятия от ряда факторов. Примером фиктивной переменной в данной модели будет являться ____________ работника
#Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является __________ потребителя
#Факторные переменные уравнения множественной регрессии, преобразованные из качественных в количественные называются …
#Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков …
#Фиктивные переменные включаются в уравнения __________ регрессии
#Одним из методов присвоения числовых значений фиктивным переменным является …
-нахождение среднего значения
-выравнивание числовых значений по убыванию
-выравнивание числовых значений по возрастанию
#Методом присвоения числовых значений фиктивным переменным не является …
+нахождение среднего значения
-присвоение цифровых меток
-присвоение количественных значений
#Величина коэффициента регрессии показывает …
+среднее изменение результата при изменении фактора на одну единицу
-характер связи между фактором и результатом
-тесноту связи между фактором и результатом
-тесноту связи между исследуемыми факторами
#Величина параметра a в уравнении парной линейной регрессии 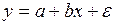
+результирующей переменной при нулевом значении фактора
-факторной переменной при нулевом значении результата
-результирующей переменной при нулевом значении случайной величины
-факторной переменной при нулевом значении случайного фактора
#Уравнение регрессии, которое связывает результирующий признак с одним из факторов при зафиксированном на среднем уровне значении других переменных называется …
#В линейном уравнении парной регрессии 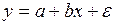
#Линейное уравнение множественной регрессии имеет вид 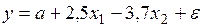
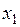
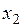
+по этому уравнению нельзя ответить на поставленный вопрос, так как коэффициенты регрессии несравнимы между собой
— 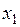
— 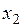
-оказывают одинаковое влияние
#В стандартизованном уравнении множественной регрессии 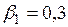
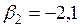
+ 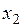
— 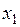
-по этому уравнению нельзя ответить на поставленный вопрос, так как стандартизованные коэффициенты регрессии несравнимы между собой
-по этому уравнению нельзя ответить на поставленный вопрос, так как неизвестны значения «чистых» коэффициентов регрессии
#Построена модель парной регрессии зависимости предложения от цены 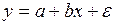
+случайной величины ε
-посредством константы ε
-случайной величины x
-посредством параметра b
#Для модели зависимости дохода населения (р.) от объема производства (млн. р.) получено уравнение у = 0,003х + 1200 + ε. При изменении объема производства на 1 млн. р. доход в среднем изменится на …
#В стандартизованном уравнении множественной регрессии переменными являются …
-средние значения исходных переменных
#Показатель, характеризующий на сколько сигм изменится в среднем результат при изменении соответствующего фактора на одну сигму, при неизменном уровне других факторов называется __________ коэффициентом регрессии
#В стандартизованном уравнении свободный член …
-равен коэффициенту множественной корреляции
-равен коэффициенту множественной детерминации
Оценка параметров линейных уравнений регрессии
#Метод наименьших квадратов используется для оценивания …
+параметров линейной регрессии
-величины коэффициента корреляции
-величины коэффициента детерминации
-средней ошибки аппроксимации
#Метод наименьших квадратов не применимдля …
+уравнений нелинейных по оцениваемым параметрам
-линейных уравнений множественной регрессии
-линейных уравнений парной регрессии
-полиномиальных уравнений множественной регрессии
#В основе метода наименьших квадратов лежит …
+минимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
-равенство нулю суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
-максимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
-минимизация суммы квадратов отклонений фактических значений результативного признака от его средних значений
#Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить …
-методом первых разностей
-методом скользящего среднего
#В исходном соотношении МНК сумма квадратов отклонений фактических значений результативного признака от его теоретических значений …
-приравнивается к нулю
-приравнивается к системе нормальных уравнений
#Метод наименьших квадратов позволяет оценить _____________ уравнений регрессии
-параметры и переменные
-переменные и случайные величины
#Оценки параметров уравнений регрессии при помощи метода наименьших квадратов находятся на основании решения …
+решения системы нормальных уравнений
-решения двойственной задачи
-решения уравнения регрессии
-решения системы нормальных неравенств
#Оценки параметров линейного уравнения множественной регрессии можно найти при помощи метода …
+метода наименьших квадратов
-метода наибольших квадратов
-метода средних квадратов
-метода нормальных квадратов
#Метод наименьших квадратов применяется для оценки …
+параметров линейных уравнений регрессии
-качества линейных уравнений регрессии
-уравнений регрессии, нелинейных по параметрам
-качества уравнений, нелинейных по параметрам
#Система нормальных уравнений метода наименьших квадратов строится на основании …
+таблицы исходных данных
-предсказанных значений результативного признака
-отклонений фактических значений результативного признака от его теоретических значений
-отклонений фактических значений объясняющей переменной от ее теоретических значений
#Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является …
-равенство нулю средних значений результативной переменной
-равенство нулю средних значений факторного признака
#Несмещенность оценки характеризует …
+равенство нулю математического ожидания остатков
-наименьшую дисперсию остатков
-увеличение точности ее вычисления с увеличением объема выборки
-ее зависимость от объема выборки
#Если оценка параметра эффективна, то это означает …
+наименьшую дисперсию остатков
-равенство нулю математического ожидания остатков
-максимальную дисперсию остатков
-уменьшение точности с увеличением объема выборки
#Состоятельность оценки характеризуется .
+увеличением ее точности с увеличением объема выборки
-независимостью от объема выборки значения математического ожидания остатков
-уменьшением ее точности с увеличением объема выборки
-зависимостью от объема выборки значения математического ожидания остатков
#Несмещенность оценки на практике означает …
+что при большом числе выборочных оцениваний остатки не будут накапливаться
-что найденное значение коэффициента регрессии нельзя рассматривать как среднее значение из возможного большого количества несмещенных оценок
-невозможность перехода от точечного оценивания к интервальному
-уменьшение точности с увеличением объема выборки
#Эффективность оценки на практике характеризуется …
+возможностью перехода от точечного оценивания к интервальному
-отсутствием накапливания значений остатков при большом числе выборочных оцениваний
-невозможностью перехода от точечного оценивания к интервальному
-уменьшением точности с увеличением объема выборки
#Свойствами оценок МНК являются …
+эффективность, состоятельность и несмещенность
-эффективность, состоятельность и смещенность
-эффективность, несостоятельность и смещенность
-эффективность, несостоятельность и несмещенность
#Увеличение точности оценок с увеличением объема выборки описывает свойство _______ оценки.
#Математическое ожидание остатков равно нулю, если оценки параметров обладают свойством …
#Минимальная дисперсия остатков характерна для оценок, обладающих свойством …
#Переход от точечного оценивания к интервальному возможен, если оценки являются …
+ эффективными и несмещенными
-эффективными и несостоятельными
-неэффективными и состоятельными
-состоятельными и смещенными
#При примени метода наименьших квадратов исследуются свойства …
+оценок параметров уравнения регрессии
-оценок переменных уравнения регрессии
-оценок случайных величин уравнения регрессии
-оценок переменных и параметров уравнения регрессии
+одинаковую дисперсию остатков при каждом значении фактора
-рост дисперсии остатков с увеличением значения фактора
-уменьшение дисперсии остаток с уменьшением значения фактора
-максимальную дисперсию остатков при средних значениях фактора
#Предпосылкой метода наименьших квадратов является то, что…
+остаточные величины имеют случайный характер
-остаточные величины имеют неслучайный характер
-при увеличении моделируемых значений результативного признака значение остатка увеличивается
-при уменьшении моделируемых значений результативного признака значение остатка уменьшается
+зависимость дисперсии остатков от значения фактора
-постоянство дисперсии остатков независимо от значения фактора
-независимость математического ожидания остатков от значения фактора
-зависимость математического ожидания остатков от значения фактора
#Предпосылкой метода наименьших квадратов является то, что остатки…
+подчиняются закону нормального распределения
-не подчиняются закону нормального распределения
-подчиняются закону больших чисел
-не подчиняются закону больших чисел
#Предпосылки метода наименьших квадратов исследуют поведение …
-параметров уравнения регрессии
-переменных уравнения регрессии
#Предпосылкой метода наименьших квадратов является …
+отсутствие автокорреляции в остатках
-присутствие автокорреляции в остатках
-отсутствие корреляции между результатом и фактором
-присутствие автокорреляции между результатом и фактором
#Предпосылкой метода наименьших квадратов не является условие …
+неслучайного характера остатков
-отсутствия автокорреляции в остатках
-случайного характера остатков
#Случайный характер остатков предполагает …
+независимость остатков от величины предсказанных по модели значений результативного признака
-зависимость остатков от величины предсказанных по модели значений результативного признака
-зависимость предсказанных по модели значений результативного признака от значений факторного признака
-независимость предсказанных по модели значений результативного признака от значений факторного признака
#Отсутствие автокорреляции в остатках предполагает, что значения ______ не зависят друг от друга
#Оценки параметров, найденные при помощи метода наименьших квадратов обладают свойствами эффективности, состоятельности и несмещенности, если предпосылки метода наименьших квадратов …
-можно не учитывать
#Если предпосылки метода наименьших квадратов нарушены, то …
+оценки параметров могут не обладать свойствами эффективности, состоятельности и несмещенности
-коэффициент регрессии является несущественным
-коэффициент корреляции является несущественным
-полученное уравнение статистически незначимо
#Обобщенный метод наименьших квадратов применяется в случае…
#Обобщенный метод наименьших квадратов используется для корректировки…
+гетероскедастичности остатков в уравнении регрессии
-автокорреляции между независимыми переменными
-параметров нелинейного уравнения регрессии
-точности определения коэффициента множественной корреляции
#Обобщенный метод наименьших квадратов подразумевает …
-линеаризацию уравнения регрессии
-двухэтапное применение метода наименьших квадратов
-переход от множественной регрессии к парной
#Обобщенный метод наименьших квадратов рекомендуется применять в случае …
-нормально распределенных остатков
-автокорреляции результативного признака
#При применении метода наименьших остатков уменьшить гетероскедастичность остатков удается путем …
-введения дополнительных факторов в модель
-введения дополнительных результатов в модель
#На основании преобразования переменных при помощи обобщенного метода наименьших квадратов получаем новое уравнение регрессии, которое представляет собой …
+взвешенную регрессию, в которой переменные взяты с весами
-нелинейную регрессию, в которой переменные взяты с весами
-взвешенную регрессию, в которой переменные взяты с весами
-нелинейную регрессию, в которой переменные взяты с весами
#Обобщенный метод наименьших квадратов не используется для моделей с _______ остатками
-автокоррелярованными и гетероскедастичными
#Что преобразуется при применении обобщенного метода наименьших квадратов?
+исходные уровни переменных
-дисперсия результативного признака
-дисперсия факторного признака
-стандартизованные коэффициенты регрессии
#Обобщенный метод наименьших квадратов отличается от обычного МНК тем, что при применении ОМНК…
+преобразуются исходные уровни переменных
-уменьшается количество наблюдений
-остатки приравниваются к нулю
-остатки не изменяются
#После применения обобщенного метода наименьших квадратов удается избежать ______ остатков
-равенства нулю суммы
#Метод оценки параметров моделей с гетероскедастичными остатками называется …методом наименьших квадратов
Видео:Математика #1 | Корреляция и регрессияСкачать

Множественная регрессия
Видео:РЕГРЕССИОННЫЙ АНАЛИЗ общая идея | АНАЛИЗ ДАННЫХ #16Скачать

Множественная линейная регрессия в скалярной и векторной формах
Уравнение множественной регрессии отражает корреляционную связь результативной (зависимой) переменной у и нескольких объясняющих (независимых) 

где у – результативная переменная (зависимая, объясняемая); 



Если в качестве функции в формуле (2.1) выбрана линейная, уравнение регрессии называется уравнением множественной линейной регрессии и имеет вид
где 
В ряде случаев удобнее пользоваться матричной записью этого уравнения
где X – матрица значений независимых переменных
Первый столбец этой матрицы состоит из единиц, которые рассматриваются как значения дополнительной переменной, на которую умножается свободный член. В матрицу X входит р независимых переменных, принимающих п значений.


Векторы Y и ε включают в себя по п значений зависимой переменной и случайных остатков, вектор а состоит из значений 


Видео:Множественная линейная регрессия, часть 1Скачать

Метод наименьших квадратов и предпосылки его применения для множественной линейной регрессии
Для определения значений параметров уравнения множественной регрессии используют числовую информацию, которая рассматривается как выборочная. Поэтому рассчитанные на ее основе величины называют оценками параметров,
подчеркивая тем самым их возможную неточность из-за неполноты информации. Оценки параметров могут меняться от выборки к выборке, поэтому они рассматриваются как случайные величины.
Далее будем различать обозначения параметров и случайных остатков, полученных по выборке (т.е. по имеющимся у исследователя данным), и значения параметров и случайных остатков по генеральной совокупности. Для обозначения выборочных значений будут использоваться латинские буквы: 



Так как найденные параметры являются лишь выборочными оценками неизвестных параметров по генеральной совокупности, то возникает вопрос об их качестве. Характеристиками качества полученных оценок параметров регрессии являются их несмещенность, эффективность и состоятельность.
Оценка параметра является несмещенной, если ее математическое ожидание равно оцениваемому параметру. Например, математическое ожидание оценки коэффициента регрессии аj равно его значению в генеральной совокупности 
Оценка параметра является эффективной, если она имеет наименьшую дисперсию среди всех возможных оценок данного параметра по выборкам одного и того же объема:
где 




Оценка параметра является состоятельной, если с увеличением числа наблюдений она стремится к значению параметра в генеральной совокупности:
Простейшим методом оценки параметров множественной регрессии является МНК. МНК-оценки будут несмещенными, эффективными и состоятельными при выполнении определенных требований, называемых предпосылками МНК. Эти требования касаются статистических свойств исходных данных:
- – независимые переменные являются неслучайными величинами, не связанными между собой;
- – зависимая переменная является случайной величиной, не ограниченной сверху или снизу;
- – для каждого набора значений независимых переменных результативная переменная рассматривается как отдельная случайная величина
. Ее распределение описывается нормальным законом с математическим ожиданием, равным выровненному значению зависимой переменной:
Например, в модели с тремя независимыми переменными имеется наблюдение номер десять 


Вторая характеристика нормального распределения – среднее квадратическое отклонение σY может быть любым, однако оно должно быть одинаковым для всех случайных величин 
– разные случайные величины 

Линейная модель регрессии, для которой выполняются эти условия, называется классической нормальной линейной моделью.
Так как случайная величина 




1. Математическое ожидание случайного остатка равно нулю:

2. Дисперсия случайных остатков одинакова для различных і и j.

3. Случайные остатки не зависят друг от друга (не автокоррелированы):

4. Случайные остатки не зависят от значений независимых переменных, входящих в модель регрессии:

5. Случайные остатки распределены по нормальному закону распределения.
Метод наименьших квадратов основывается на принципе минимизации квадратов отклонений фактических значений результативного признака у от его выровненных значений у, рассчитанных по уравнению регрессии

Для множественной линейной регрессии выражение (2.6) будет иметь вид
Для нахождения экстремума по каждому из неизвестных параметров 


После преобразований система уравнений (2.7) имеет вид

Система (2.8) называется системой нормальных уравнений. В матричной форме применение МНК приводит к следующему результату:

Пример
Имеются статистические данные о значениях четырех показателей в разрезе 48 субъектов РФ, которые приведены в табл. 2.1.
- 1. Поступление налогов, сборов и иных обязательных платежей в консолидированный бюджет РФ (без поступлений ЕСН) в 2009 г., млн. руб.
- 2. Количество занятых в Российской Федерации в 2009 г., тыс. человек.
- 3. Объем отгруженных товаров собственного производства, выполненных работ и оказанных услуг собственными силами по виду экономической деятельности «Обрабатывающие производства» в Российской Федерации в 2009 г., млн руб.
- 4. Объем отгруженных товаров собственного производства, выполненных работ и услуг собственными силами по виду экономической деятельности «Производство и распределение электроэнергии, газа и воды» в Российской Федерации в 2009 г., млн руб.
Предположим, что зависимой переменной y в данном случае является «поступление налогов, сборов и иных обязательных платежей в консолидированный бюджет РФ». Для краткости будем называть эту переменную «поступление налогов». Независимыми переменными являются остальные три переменные, которые мы будем называть и обозначать как «количество занятых» 



Таблица 2.1. Некоторые экономические показатели деятельности субъектов РФ в 2009 г.
Субъект РФ
Поступление налогов, млн руб.
Количество занятых, тыс. человек
Отгрузка в обрабатывающих производствах, млн руб.
Производство энергии, млн руб.
Еврейская автономная область
Республика Северная Осетия – Алания
Чукотский автономный округ
Республика Марий Эл
Источник: данные Росстата.
Применяя к исходным данным (см. табл. 2.1) МНК, оценим параметры регрессии. Система нормальных уравнений для нашего примера имеет вид
После вычислений получаем уравнение
Из уравнения регрессии следует, что между сбором налогов и независимыми переменными, входящими в модель, наблюдается прямая связь. Напомним, что коэффициенты при независимых переменных называются коэффициентами регрессии. Они являются абсолютными показателями силы связи и характеризуют среднее изменение зависимой переменной при единичном изменении независимой переменной – сомножителя данного коэффициента при условии неизменности остальных независимых переменных, включенных в уравнение (модель) регрессии.
В частности, можно сделать вывод, что с изменением количества занятых на 1 тыс. человек поступление налогов в среднем изменится в ту же сторону на 12,45 млн руб. при неизменном объеме отгрузки в обрабатывающих производствах и производстве энергии.
Изменение объема отгрузки в обрабатывающих производствах на 1 млн руб. приведет к изменению поступления налогов в среднем на 0,06 млн руб. при неизменных значениях количества занятых и производства энергии.
При изменении производства энергии на 1 млн руб. поступление налогов в среднем изменится на 0,31 млн руб. при неизменных значениях количества занятых и объема отгрузки в обрабатывающих производствах.
Величины коэффициентов регрессии определяются не только силой связи между показателями, но и масштабом их измерения, и поэтому несравнимы между собой. Для сопоставления независимых переменных по силе их влияния на результативную используют относительные показатели силы связи – коэффициенты эластичности.
Общая формула коэффициента эластичности по переменной Xj имеет вид
где 



Отметим, что коэффициенты эластичности могут быть рассчитаны для любой функции – как линейной, так и нелинейной. Например, для множественной линейной регрессии коэффициент эластичности по переменной х; будет равен

Из формулы (2.10) следует, что коэффициент эластичности для линейной функции зависит от конкретных значений независимых переменных, включенных в модель. Так как коэффициент эластичности измеряет влияние переменной xj на переменную y, то значения остальных независимых переменных принято фиксировать на их среднем уровне:
Таким образом, при фиксированных значениях других переменных существует целый ряд коэффициентов эластичности по переменной 



Как следует из МНК для линейной регрессии, выражение в знаменателе (2.11) равно среднему значению зависимой переменной, что позволяет упростить формулу:
Коэффициенты эластичности показывают, на сколько процентов в среднем изменится зависимая переменная при изменении переменной 

Рассмотрим средние коэффициенты эластичности для регрессии, полученной в примере 2.1.
Для характеристики силы связи количества занятых и поступления налогов рассчитаем коэффициент эластичности
Следовательно, с изменением количества занятых на 1% от среднего уровня поступление налогов в среднем изменится в ту же сторону на 0,32% своего среднего уровня при неизменном объеме отгрузки в обрабатывающих производствах и производстве энергии.
Коэффициенты эластичности для переменных «объем отгрузки в обрабатывающих производствах» и «производство энергии» рассчитываются и интерпретируются аналогично. Они равны
Сопоставляя полученные коэффициенты эластичности, можно сделать вывод о том, что наиболее сильное влияние на сбор налогов оказывает число занятых.
Другими относительными показателями силы связи являются стандартизованные коэффициенты регрессии. В отличие от коэффициентов эластичности, они рассчитываются только для случая множественной линейной регрессии по формуле
Для примера 2.1 стандартизованные коэффициенты регрессии равны
Стандартизованные коэффициенты регрессии могут быть проинтерпретированы. Величина 




Сопоставление стандартизованных коэффициентов регрессии для примера 2.1 приводит к другим, чем по коэффициентам эластичности, выводам о том, какая переменная оказывает более сильное влияние на результативную переменную. В данном случае это 
где 


Стандартизованные коэффициенты регрессии являются коэффициентами в функции регрессии, построенной на основе стандартизованных переменных – переменных, полученных в результате преобразования исходных данных по формулам
где 



Уравнение регрессии, включающее стандартизованные переменные, называют уравнением регрессии в стандартизованном масштабе (форме, виде):

где 
Так как уравнение 
Особенностью уравнения регрессии в стандартизованном масштабе является отсутствие в нем свободного члена. Это свойство является следствием двух утверждений:
- – среднее значение стандартизованной переменной равно нулю;
- – свободный член уравнения множественной линейной регрессии равен
Таким образом, прямая, построенная на основе уравнения регрессии в стандартизованном масштабе, всегда проходит через начало координат. Этим же свойством обладает уравнение регрессии, построенное на основе центрированных переменных, которые рассчитываются по формулам

При использовании центрированных переменных коэффициенты регрессии и случайные остатки равны коэффициентам регрессии и случайным остаткам уравнения в натуральном масштабе:

На рис. 2.1 дана геометрическая интерпретация МНК для множественной линейной регрессии. Каждую переменную, образующую столбец матрицы X, можно рассматривать как вектор-столбец 











Так как вектор 

Рис. 2.1. Геометрическая интерпретация ΜΗΚ
Из последнего выражения следует, что вектор параметров а или равен нулю (нулевая проекция, вектор Υ ортогонален векторам X, переменная / не зависит от переменных х), или
Таким образом, на основе геометрической интерпретации мы получили ту же формулу для оценки параметров регрессии, что и аналитическим путем.
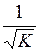
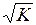







 . Ее распределение описывается нормальным законом с математическим ожиданием, равным выровненному значению зависимой переменной:
. Ее распределение описывается нормальным законом с математическим ожиданием, равным выровненному значению зависимой переменной:




















