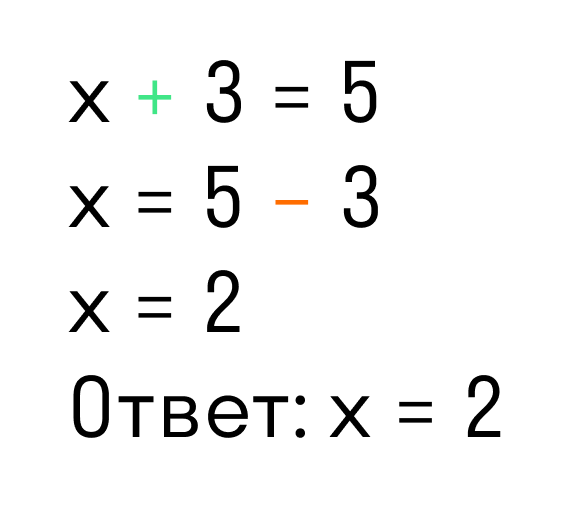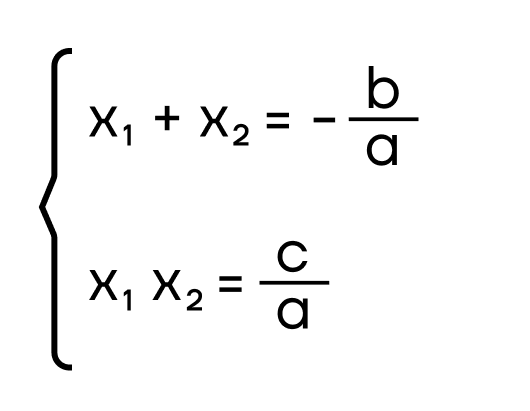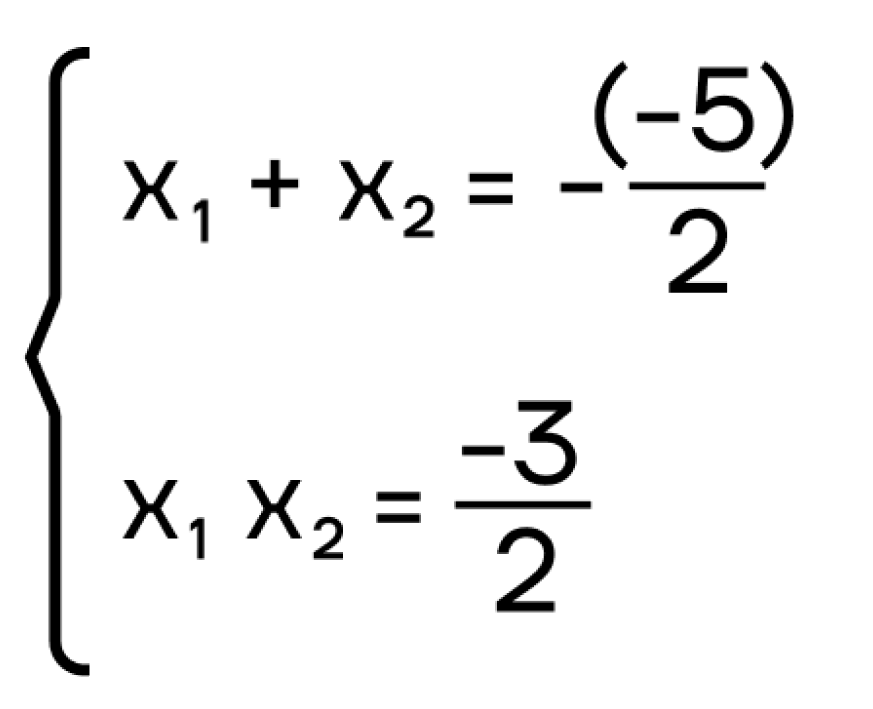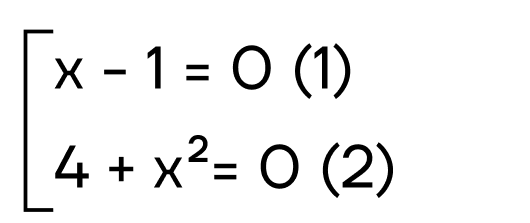Линейное уравнение это уравнение вида где и числа неизвестное

Линейные уравнения — относительно несложная математическая тема, довольно часто встречающаяся в заданиях по алгебре. Разберемся, что это такое, и как решаются линейные уравнения.

Как правило, линейное уравнение — это уравнение вида ax + c = 0, где а и с — произвольные числа, или коэффициенты, а х — неизвестное число.

К примеру, линейным уравнением будет:

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Решение линейных уравнений.

Как решать линейные уравнения?

Решаются линейные уравнения совсем несложно. Для этого используются такой математический прием, как тождественное преобразование. Разберем, что это такое.

Пример линейного уравнения и его решение.

Пусть ax + c = 10, где а = 4, с = 2.

Таким образом, получаем уравнение 4х + 2 = 10.

Для того чтобы решить его было проще и быстрее, воспользуемся первым способом тождественного преобразования — то есть, перенесем все цифры в правую часть уравнения, а неизвестное 4х оставим в левой части.

Таким образом, уравнение сводится к совсем простенькой задачке для начинающих. Остается лишь воспользоваться вторым способом тождественного преобразования — оставив в левой части уравнения х, перенести в правую часть цифры. Получим:

4х + 2 = 10, где х = 2.

График линейного уравнения.

При решении линейных уравнений с двумя переменными также часто используется метод построения графика. Дело в том, что уравнение вида ах + ву + с = 0, как правило, имеет много вариантов решения, ведь на место переменных подходит множество чисел, и во всех случаях уравнение остается верным.

Поэтому для облегчения задачи выстраивается график линейного уравнения.

Чтобы построить его, достаточно взять одну пару значений переменных — и, отметив их точками на плоскости координат, провести через них прямую. Все точки, находящиеся на этой прямой, и будут вариантами переменных в нашем уравнении.

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Решение простых линейных уравнений

О чем эта статья:

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

если а = 0 — уравнение корней не имеет;

если а и b равны нулю, то корнем уравнения является любое число.

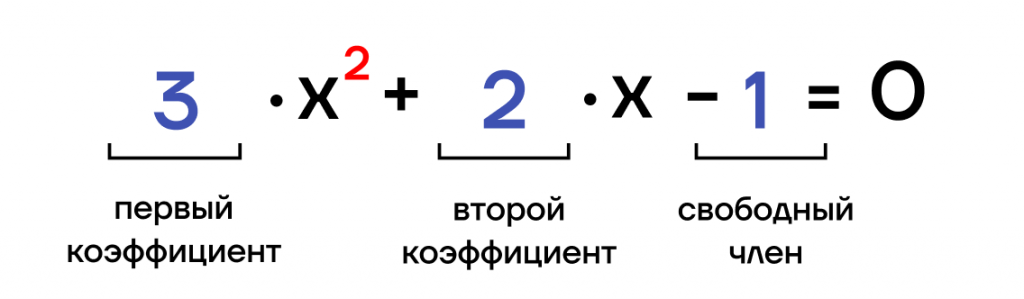
Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:Уравнение. 5 класс.Скачать

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

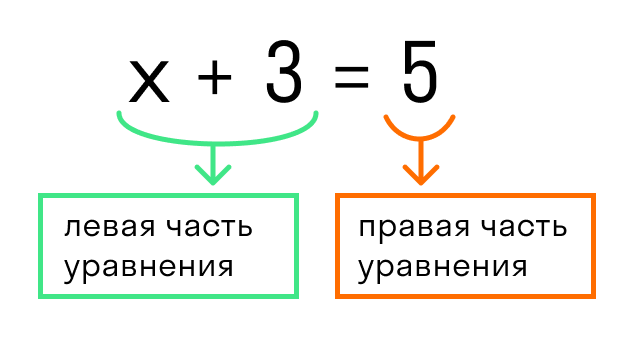
Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

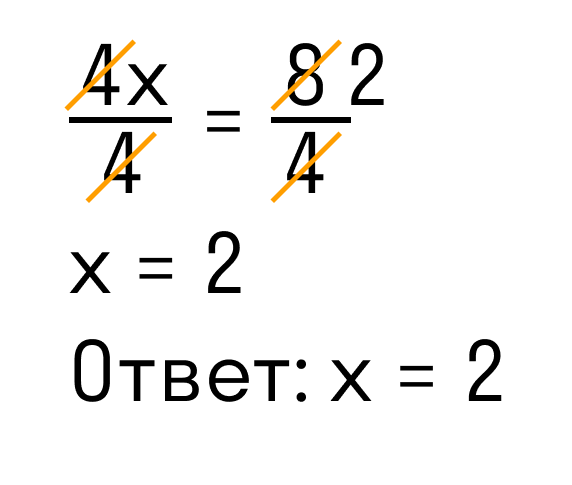
Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

-4x = 12 | : (-4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Линейные, квадратные и кубические уравнения

На этой странице вы узнаете:

• Почему неизвестное обозначают через x?
• Как находить корни квадратного уравнения, не считая их?
• Как дискриминант может повлиять на количество корней уравнения?

Видео:Линейное уравнение с одним неизвестным.Скачать

Понятие уравнения

Главный секрет математики в том, что любую задачу можно решить уравнением. А решить уравнение – значит найти все его корни или доказать, что их нет.

Давай разберемся как это сделать.

Уравнение – это равенство, содержащее неизвестное, обозначенное буквой.

Корнем уравнения называется такое значение неизвестного, при котором уравнение становится верным равенством.

Например, число 8 будет корнем уравнения 2x — 3 = 5 + x, потому что равенство 2 * 8 — 3 = 5 + 8 верное.

Видео:Алгебра 7 класс (Урок№43 - Решение линейных уравнений с одним неизвестным.)Скачать

Линейные уравнения

Что же такое линейное уравнение?

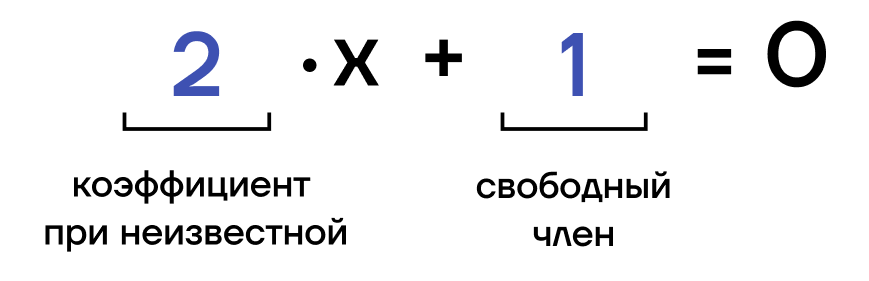
Линейное уравнение – это уравнение, в котором неизвестная находится в степени 1.

Вид линейного уравнения:

ax + b=0 , где
х – неизвестная
а – коэффициент при неизвестной
b – свободный член

Стоит отметить, что а и b в таком уравнение известны, также оба этих числа можно называть коэффициентами.

Как же решить такое уравнение?

Для решения линейного уравнения нужно выразить х и найти числовое значение, то есть сделать такие преобразования, чтобы в одной части уравнения осталась только неизвестная, а в другой собралось все остальное.

Преобразования, которые можно совершать:

1. Переносить слагаемое в другую часть уравнения с противоположным знаком.

x — 5 = 0
x = 0 + 5
x = 5

1. Умножать или делить обе части уравнение на одно и то же число или выражение, которое не равно нулю.

Давайте рассмотрим решение линейного уравнения на следующем примере

2(x + 5) — 4x + 2 = 0

1. Сначала раскроем скобки
   2x + 10 — 4x + 2 = 0

1. Для упрощения сложим подобные слагаемые
   -2x + 12 = 0

1. Теперь перенесем слагаемое без неизвестной в правую часть и разделим обе части уравнения на коэффициент при неизвестной, то есть выразим х
   -2x = -12 | : (-2)
   x = 6

Значение неизвестной найдено, а значит единственное решение данного уравнения 6

С линейными уравнениями можно столкнуться и в жизни.

Допустим, нам нужно приготовить 570 грамм теста на пирожки.

Обозначим вес одной части за x. Составим и решим уравнение для получения этого количества теста:

12x + 6x + x = 570
19x = 570
x = 30

Мы узнали, что одна часть — это 30 грамм. Теперь посчитаем сколько грамм продуктов нам потребуется.

• Мука: 12 * 30 = 360 грамм
• Вода: 6 * 30 = 180 грамм
• Растительное масло: 1 * 30 = 30 грамм

Видео:Линейное уравнение. Что это?Скачать

Квадратные уравнения

Мы уже знаем, что такое линейное уравнение. Но как же выглядит квадратное?

Квадратное уравнение – это уравнение, в котором неизвестная находится в степени 2.

Вид квадратного уравнения:

ax 2 + bx + c = 0 , где
х — неизвестная
а и b – коэффициенты при неизвестной
с – свободный член

Стоит отметить, что а, b и с – известные числа.

Какими бывают квадратные уравнения?

Эти виды квадратных уравнений отличаются тем, что у полного квадратного уравнения есть оба коэффициента и свободный член, а у неполного может отсутствовать или второй коэффициент, или свободный член.

Решение несколько неполных квадратных уравнений на примере:

x 2 + 2x = 0 x * (x + 2) = 0 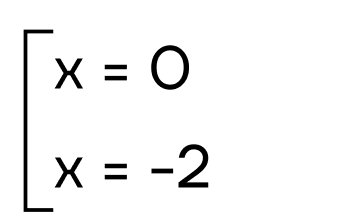Ответ: 0 и -2

x 2 — 4 = 0 x 2 = 4 x = ±2 Ответ: 2 и -2

Полное квадратное уравнение может иметь 2 корня, 1 корень или не иметь корней. Количество корней зависит от дискриминанта

Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Что такое дискриминант?

Дискриминант в квадратном уравнении — это выражение, которое ищется по следующей формуле, где а, b и с берутся из уравнения:

D = b 2 — 4 ⋅ a ⋅ c

Как дискриминант может повлиять на количество корней уравнения? Если D > 0, то уравнение имеет 2 корня. Если D = 0, то уравнение имеет 1 корень. Если D Дискриминант нужен не только для определения количества корней, но и для их нахождения одним из способов. Способы решения квадратных уравнений: Решение через дискриминант Корни квадратного уравнения находятся по этим формулам, где а и b берутся из уравнения, а D – это дискриминант: По теореме Виета Как находить корни квадратного уравнения, не считая их? По теореме Виета корни нужно подбирать, поэтому она удобна для нахождения рациональных корней. Данная теорема заключается в связывании корней уравнения и коэффициентов многочлена системой двух уравнений. где а, b и с – коэффициенты квадратного уравнения x1 и x2 – корни квадратного уравнения Давайте рассмотрим решение квадратного уравнения на следующем примере 1 способ: D = (-5) 2 — 4 ⋅ 2 ⋅ (-3) = 25 + 24 = 49 Дискриминант больше нуля, следовательно, у уравнения 2 корня, найдем их Решениями уравнения являются числа 3 и -12. 2 способ: Запишем систему по теореме Виета Теперь подберем такие два числа, чтобы их сумма была (frac), а произведение -(frac), это будут числа 3 и -12. 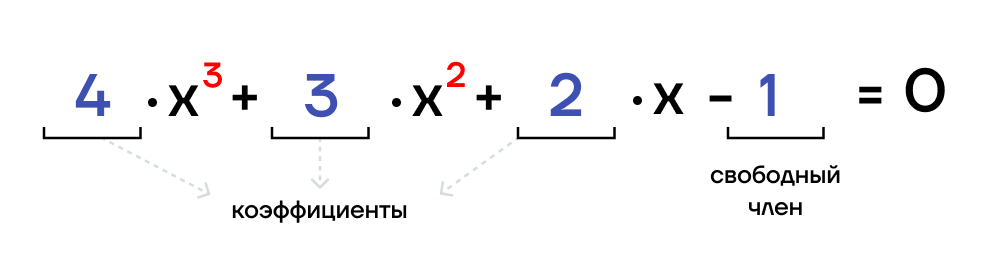Значит, решениями уравнения являются числа 3 и -12. Видео:ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать Кубические уравнения Перейдем к последнему виду уравнений. Что же такое кубическое уравнение и как оно выглядит? Кубическое уравнение – это уравнение, в котором неизвестная находится в степени 3. Вид кубического уравнения: ax 3 + bx 2 + cx + d = 0, где х — неизвестная а, b и с – коэффициенты при неизвестной d – свободный член Стоит отметить, что а, b, с и d – известные числа. Преобразования, которые можно совершать в кубических уравнениях: Вынесение общего множителя за скобки. Вынесение общего множителя за скобки можно сравнить с делением фруктов в обеих тарелках на одинаковые части и вынесением такой части в отдельную тарелку. Алгоритм: Разложить каждое слагаемое на множители. Вынести за скобку множители, которые есть в обоих слагаемых. Вынести скобку, как общий множитель. x 3 — 2x 2 — 3x = x * x * x — 2 * x * x — 3 * x = x * (x 2 — 2x — 3) Группировка Алгоритм: Объединить слагаемые в пары. Вынести общий множитель из каждой скобки, чтобы получились одинаковые скобки. 6x 3 + 9x 2 + 8x + 12 = (6x 3 + 9x 2 ) + (8x + 12) = 3x 2 * (2x + 3) + 4 * (2x + 3) = = (3x 2 +4) * (2x+3) Рассмотрим решение кубического уравнения 4x + x 3 = x 2 + 4 Перенесем все слагаемые в левую часть 4x + x 3 — x 2 — 4 = 0 Заметим, что удобнее группировать 1 и 2 слагаемые и 3 и 4 слагаемые (4x + x 3 ) — (x 2 + 4) = 0 Вынесем общий множитель х из первой скобки x * (4 + x 2 ) — (x 2 + 4) = 0 Вынесем ещё один общий множитель x 2 + 4 за скобки (x — 1) * (4 + x 2 ) = 0 Чтобы произведение было равно 0, один из множителей должен быть равен 0, запишем совокупность Решим каждое уравнение отдельно x — 1 = 0 x = 1 4 + x 2 = 0 x 2 = -4 Нет решений, так как x 2 ≥ 0 верно для любого х Из этого следует, что у данного уравнения есть только одно решение x=1 Видео:Как решить уравнение #россия #сша #америка #уравненияСкачать Фактчек В линейном уравнении неизвестная находится в степени 1. Для решения такого уравнения в одной части уравнения нужно оставить только неизвестную, а в другой собрать все остальное. В кубическом уравнении неизвестная в квадрате, то есть в степени 2. Решать такое уравнение можно через дискриминант или по теореме Виета В кубическом уравнении неизвестная находится в кубе, то есть в степени 3. Для решения такого уравнения используется вынесение общего множителя за скобки и способ группировки. Видео:СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать Проверь себя Задание 1. Найдите корень уравнения (2x + 4) ⋅ 3 — 2x = 0 Задание 2. Сколько корней будет у уравнения x 2 + x — 2 = 0? Нет корней Один корень Два корня Три корня Задание 3. Найдите корни уравнения x 2 + 4x — 5 = 0 Задание 4. Найдите корни уравнения x 2 — 5x = 0 Задание 5. Найдите корни уравнения 12x + 4 — 12x 3 — 4x 2 =0 Ответы: 1. — 4; 2. — 3; 3. — 2; 4. -1; 5. — 3 🔍 Видео Уравнения. 5 классСкачать 7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать Решение уравнений, 6 классСкачать Как решать линейные уравнения #математика #математика7классСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства