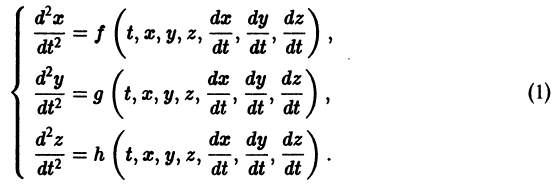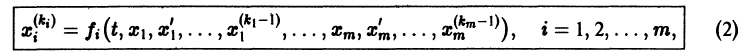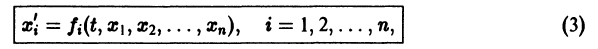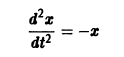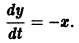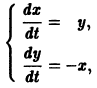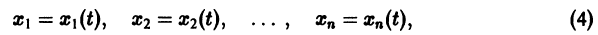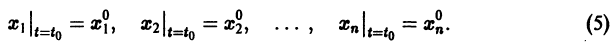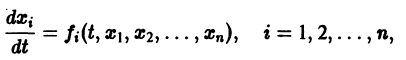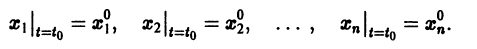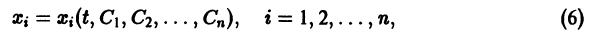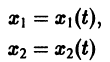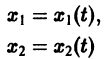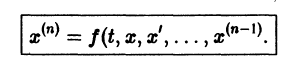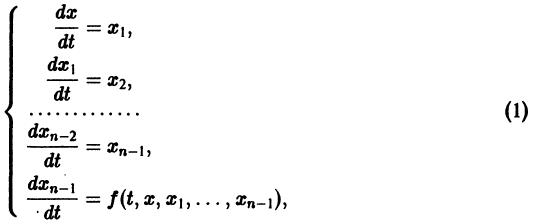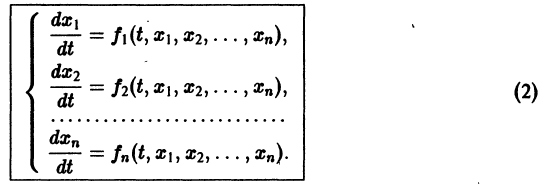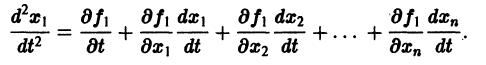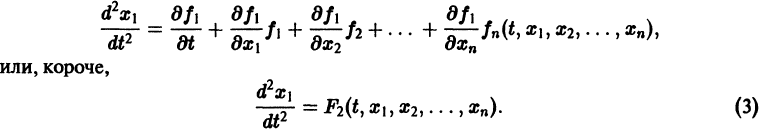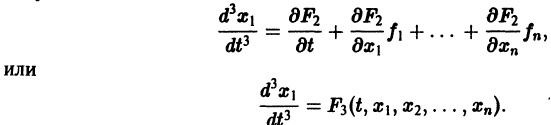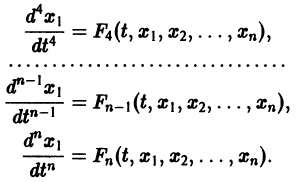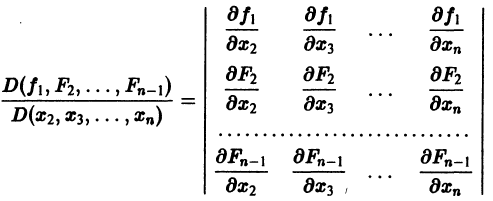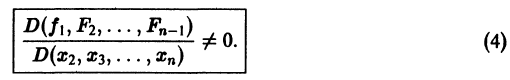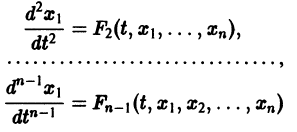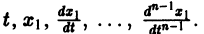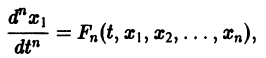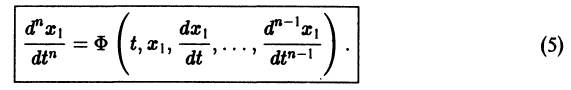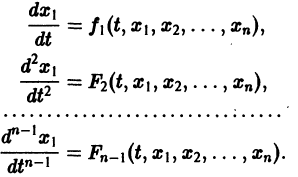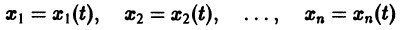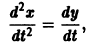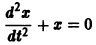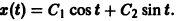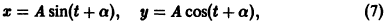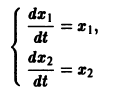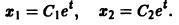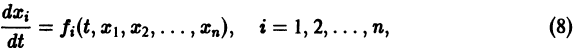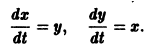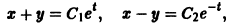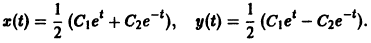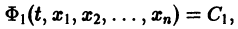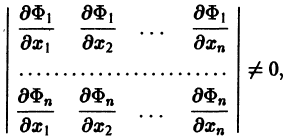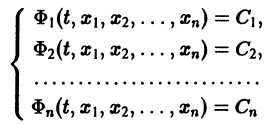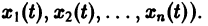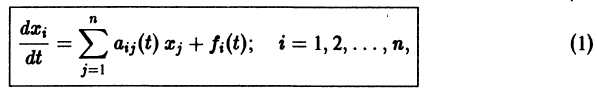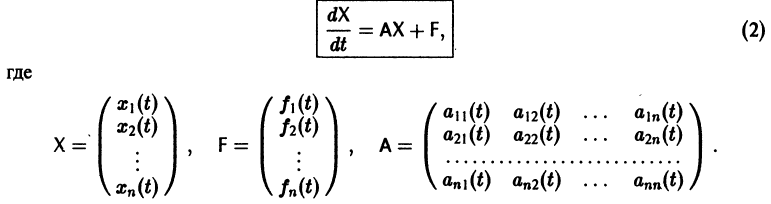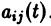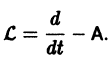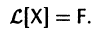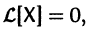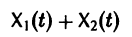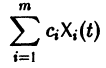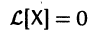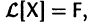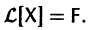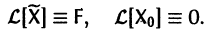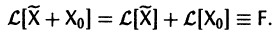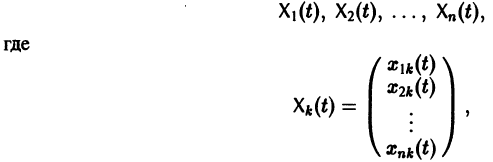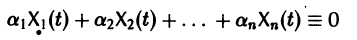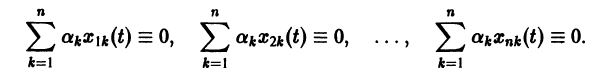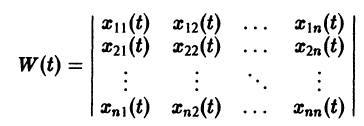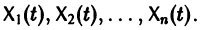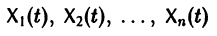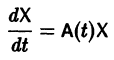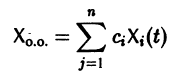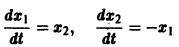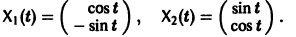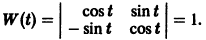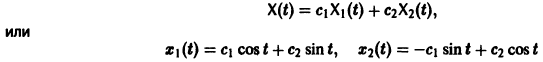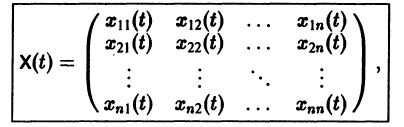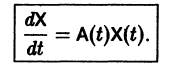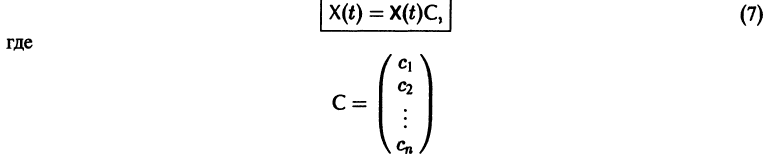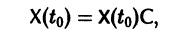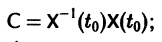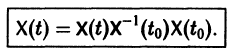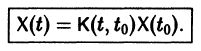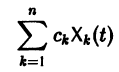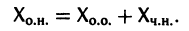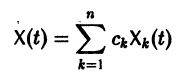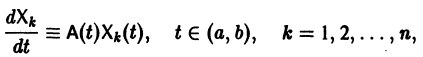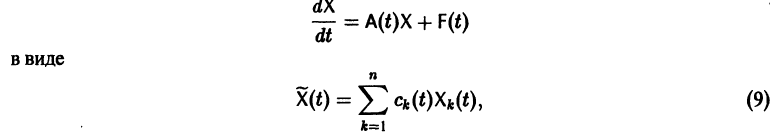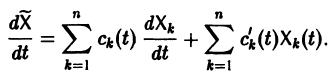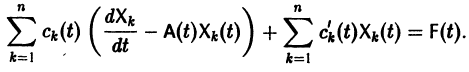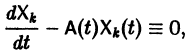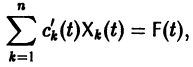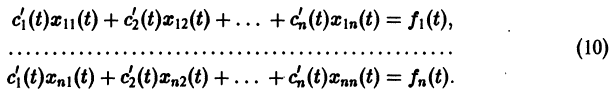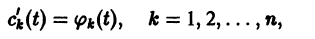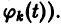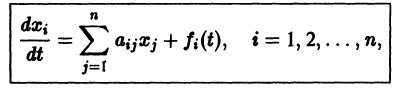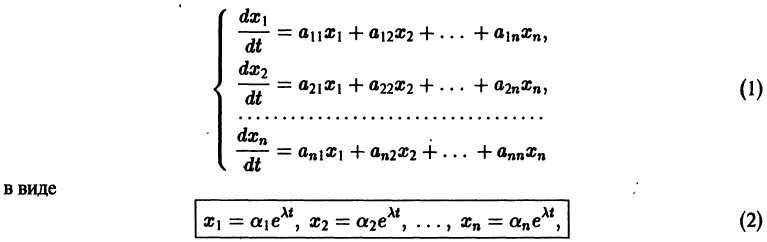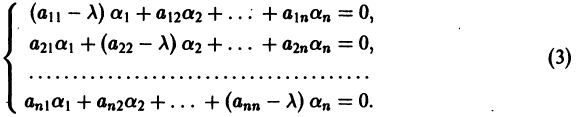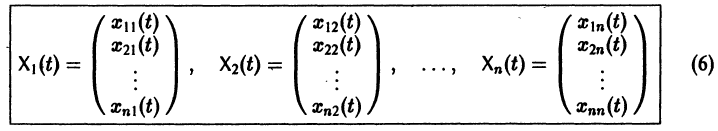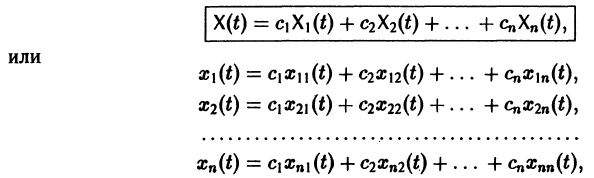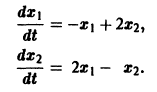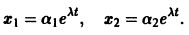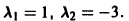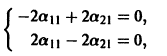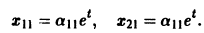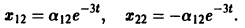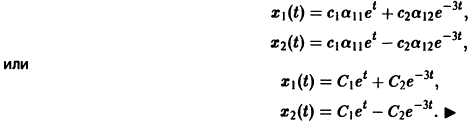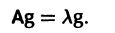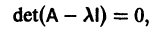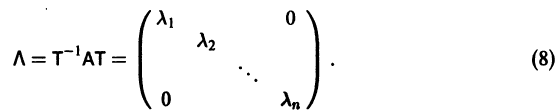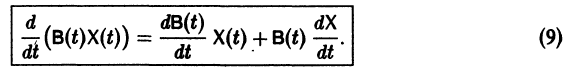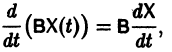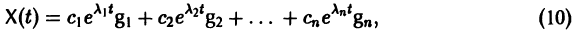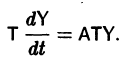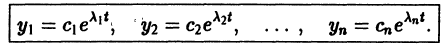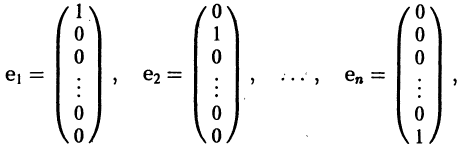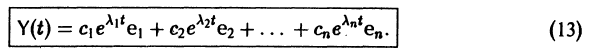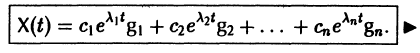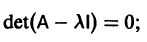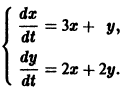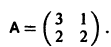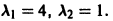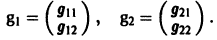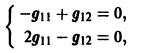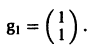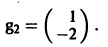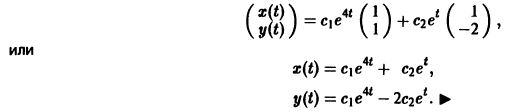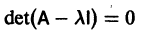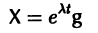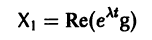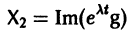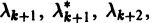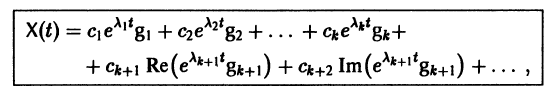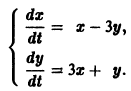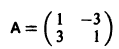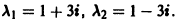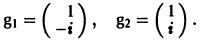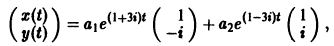По этой ссылке вы найдёте полный курс лекций по математике:
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы дифференциальных уравнений с помощью подходящим образом выбранной функции v(t, 2], 22. ж„) — так называемой функции Ляпунова, причем делается это без предварительного построения решения системы; в этом неоценимое преимущество метода. Ограничимся рассмотрением автономных систем для которых , есть точка покоя. Идея метода состоит в следующем.
Предположим, что на устойчивость исследуется точка покоя системы (1). Если бы с возрастанием t точки всех траекторий приближались к началу координат или хотя бы не удалялись от него, то рассматриваемая точка покоя была бы устойчивой. Проверка выполнения этого условия не требует знания решений системы. Действительно, если р — расстояние от точки траектории , до начала координат (производная вдоль траектории); Правая часть в (2) есть известная функция от ж„, и можно .исследовать ее знак.
Если окажется, что $0, тоточкннавс^с тдаедориях^удадоютая откачала координат щ>иэозрастрйии иточкапокояж, , устойчива. Однако точка покоя может бьггь устойчивой и при немоно» трнном пркбдажрда £ точе* траекторий (например, в случае, когда траектории — эллипсы). Поэтому А. М.Ляпунов вместо функции р рассматривал функции являющиеся в некотором смысле «обобщенным расстоянием» of начала координат. Определение 1.
Функция определенная в некоторой окрестности начала координат, называется знакоопределенной (знакоположительной или знакоотрица-телъной), если в области G где h — достаточно малое положительное число, она может принимать значения только одного определенного знака и обращается в нуль лишь при Так, в случав п = 3 функции Метод функций Ляпунова теорема Липунова об асимптотической устойчивости Устойчивость по первому (линейному) приближению будут знакоположительными, причем здесь величина может быть взята сколь угодно большой. Определение 2.
Функция называется знакопостоянной (положительной или отрицательной), если она в области G может принимать значения только одного определенного знака, но может обращаться в нуль и при . Например, функция будет знакопостоянной (положительной). В самом деле, функцию ) можно представить так: отсюда видно, что она неотрицательна всюду, но обращается в нуль и при , а именно при и любых Х|, XI таких, что Пусть — дифференцируемая функция своих аргументов, и пусть являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1).
Тогда для полной производной функции t; по времени имеем Определение 3. Величина ^, определяемая формулой (3), называется полной производной функции v по времени, составленной в силу системы уравнений (1). Определение 4. Функций .у обладающую свойствами: дифференцируема в некоторой окрестности О начала координат; 3) полная производная £ функции срставденная в силу системы (1), . всюду в П, называют функцией Ляпунова. Теорема 3 (теорема Липуноеа об устойчиюстм).
Если для системы дифференциальных уравнений существует дифференцируемая знакоопределенная функция полная производная J которой по времени, составленная в силу системы (1), есть знакопостоянная функция (знака, противоположного с v) или тождественно обращается в ноль, то точка покоя ) системы (1) устойчива. Приведем идею доказательства.
Возможно вам будут полезны данные страницы:
Пусть для определенности есп» знакоположительная функция, для которой как причем v = 0 лишь при то начало координат есть точка строгого минимума функции хп). В окрестности начала координат поверхности уровня функции v являются, как можно показать, замкнутыми поверхностями, внутри которых находится начало координат. Чтобы картина стала нагляднее, остановимся на случае . Так как v0 для малых только для то поверхность в общих чертах напоминает параболоид, вогнутый вверх (рис. 19).
Линии уровня = С представляют собой семейство замкнутых кривых, окружающих начало координат. При этом если то линия уровня целиком лежит внутри области, ограниченной линией v = С2. Зададим е > 0. Придо-статочно малом С линия уровня v = С целиком лежит в £-окрестности начала координат, но не проходит через начало. Следовательно, можно выбрать 6 > 0 такое, что окрестность начала координат целиком лежит внутри области, ограниченной линией v = Су причем в этой окрестности .
Рассмотрим траекторию системы (1), выходящую в начальный момент времени t = to из какой-нибудь точки -окрестнрсти начала координат.
Эта траектория при возрастании t никогда не пересечет ни одной из линий v(x,x2) изнутри наружу. В самом деле, если бы такое пересечение было возможным в какой-нибудь точке, то в этой точке или в ее окрестности функция необходимо имела бы положительную производную t так как при переходе от какой-нибудь линии v = С к другой линии этого семейства, охватывающей первую, функция v(x, х<) возрастает. Но это невозможно в силу того, что по условию .
Значит, если в начальный момент времени какая-нибудь траектория находилась внутри области, ограниченной линией v = С, тоона и в дальнейшем будет все время оставаться внугри этой области. Отсюда ясно, что для всякого е > 0 существует 6 > 0 такое, что любая траектория системы, выходящая в начальный момент времени t = to из ^-окрестности начала координат, для всех t ^ t0 будет содержаться в £-окрестности начала. Это и означает устойчивость точки покоя я, системы (1).
Теорема 4 (теорема Ляпунова об асимптотической устойчивости). Если для системы дифференциальных уравнений существует дифференцируемая знакоопределенная функция , полная производная которой по времени, составленная в силу системы, есть также знакоопреде-ленная функция знака, противоположного с v, то точка покоя п, системы (1) асимптотически устойчива. Пример. Исследовать на устойчивость точку покоя 0(0,0) системы 4
Выберем в качестве функции функцию Метод функций Ляпунова теорема Липунова об асимптотической устойчивости Устойчивость по первому (линейному) приближению Эта функция знакоположительная. В силу системы ) найдем Из теоремы 3 следует1, что точка покоя системы устойчива (центр). Асимптотической устойчивости нет, так как траектория системы — окружности. Пример 2. Исследовать на устойчивость точку покоя 0(0,0) системы Беря опять найдем
Таким образом, £ есть знакоотрицательная функция. В силу теоремы 4 точка покоя системы устойчива асимптотически. Теорема 5 (о неустойчивости). Пусть для системы дифференциальных уравнений существует дифференцируемая в окрестности начала координат функция такая, что Если ее полная производная составленная в силу системы (4), есть знакоположительная функция и сколь угодно близко от начала координат имеются точки, в которых функция принимает положительные значения, то точка покоя системы (4) неустойчива.
Пример 3. Исследовать не устойчивость точку покоя системы Возьмем функцию Для нее функция знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > 0 (например, вдоль прямой , то выполнены все условия теоремы 5 и точка покоя неустойчива (седло). Метод функций Ляпунова оказывается универсальным и эффективным для широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно общего конструктивного способа построения функций Ляпунова пока нет.
| В простейших случаях функцию Ляпунова |
можно искать в виде — Устойчивость по первому (линейному) приближению Пусть имеем систему дифференциальных уравнений и пусть естьточка покоя системы, Будем предполагать, что функций дифференцируемы в окрестности начала координат достаточное число раз. Применяя формулу Тейлора, разложим функциипо х в Ькрестности качала координат: или, учитывая (2), где . а слагаемые Я, содержат члены не ниже второго порядка малости относительно .
Система дифференциальных уравнений (1) примет вид Так как понятие устойчивости точки покоя связано с малой окрестностью начала координат в фазовом пространстве, то естественно ожидать, что поведение решения (1) будет определяться главными линейными членами разложения функций fi по ж. Поэтому наряду с системой (3) рассмотрим систему называемую системой уравнений первого (линейного) приближения для системы (3). Вообще говоря, строгой связи между системами (3) и (4) нет.
Рассмотрим, например, уравнение Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид Решение x(t) = 0 уравнения (6) является устойчивым. Оно же, будучи решением исходного уравнения (5), не является для него устойчивым. В самом деле, каждое действительное решение уравнения (5), удовлетворяющее начальному условию имеет вид и перестает существовать при t = — (решение непродолжаемо вправо). Теорема 6.
Если все корни характеристического уравнения имеют отрицательные действительные части, то точка покоя ,. системы (4) и системы (3) асимптотически устойчива. При выполнении условий теоремы возможно исследование на устойчивость по первому приближению. Теорема 7. Если хотя бы один корень характеристического уравнения (7) имеет положительную действительную часть, то точка покоя ж, = 0 системы (4) и системы (3) неустойчива.
В этом случае также возможно исследование на устойчивость по первому приближению. Наметим идею доказательства теорем 6 и 7. -4 Пусть для простоты корни „ характеристического уравнения (7) — действительные и различные. В этом случае существует такая невырожденная матрица Т с постоянными элементами, что матрица Т-‘AT будет диагональной: Система (3) при том же преобразовании перейдет в систему причем в R< опять входят члены не ниже второго порядка малости относительно Рассмотрим следующие возможности:
Все корни — отрицательные, Положим тогда производная £ в силу системы () будет иметь вид при — малая более высокого порядка, чем квадратичная Таким образом, в достаточно малой окрестности fi точки функция |, знакоположительна, а производная ^f — знакоотрицательна, и, значит, точка покоя асимптотически устойчива. 2. Некоторые из корней (например, положительные, а остальные — отрицательные. Положим тогда Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например, такие, у которых .
Что касается производной то, поскольку отрицательны, производная — знакоположительная функция. В силу теоремы 5 точка покоя 0(0,0. 0) неустойчива. В критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (3) начинают влиять нелинейные члены Ri и исследование на устойчивость по первому приближению становится невозможным.
Пример 1. Исследовать на устойчивость по первому приближению точку покоя системы Система первого приближения имеет вид Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем характеристическое уравнение для системы Корни характеристического уравнения . Поскольку , нулевое решение системы неустойчиво. Пример 2. Исследуем на устойчивость точку покоя 0(0, 0) системы « Точка покоя системы асимптотически устойчива, так как для этой оистемы функция Ляпунова удовлетворяет условиям теоремы Ляпучора об асимптотической устойчивости. В частности.
В то же время точка покоя системы неустойчива. В самом деле, для функции в силу системы (»») имеем функция знакоположительная. Сколь угодно близко от начала координат 0(0,0) имеются точки, в которых В силу теоремы 5 заключаем о неустойчивости точки покоя 0(0,0) системы (*»). Для системы (*) и (**) система первого приближения одна и та же: Характеристическое уравнение для системы () имеет чисто мнимые корни — критический случай (действительные части корней характеристического уравнения равны нулю).
Для системы первого приближения ( качало координат является устойчивой точкой покоя — центром. Системы ) получаются малым возмущением правых частей в окрестности начала координат. Однако эти малые возмущения приводят к тому, что для системы (*) точка покоя ) становится асимптотически устойчивой, а для системы (*t) — неустойчивой. Этот пример показывает, что в критическом случае нелинейные члены могут влиять на устойчивость точки покоя. Задам.
Исследовать на устойчивость точку покоя 0(0,0) системы где функция /(х, у) разлагается в сходящийся отеленной ряд и Упражнения Метод функций Ляпунова теорема Липунова об асимптотической устойчивости Устойчивость по первому (линейному) приближению Пользуясь определением, исследуйте на устойчивость решения уравнений: Установите характер точки покоя системы и нарисуйте расположение траекторий в окрестности этой точки:
Методом функций Ляпунова исследуйте на устойчивость точку покоя 0(0,0) систем: Исследуйте на устойчивость по первому (линейному) приближению точку покоя 0(0,0) . систем: 1. Асимптотически устойчиво. 2. Неустойчиво. 3. Устойчиво. 4. Устойчивый узел. 5. Седло. 6. Устойчивый фокус. 7. Центр. 8. Асимптотически устойчива, v = 7х2 + у2. 9. Устойчива, v = х2 + у2. 10. Неустойчива, х2 — у2. 11. Асимптотически устойчива. 12. Неустойчива.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
- Устойчивость решений ДУ по первому приближению
- Устойчивость решений ДУ по отношению к изменению правых частей уравнений
- Системы дифференциальных уравнений с примерами решения и образцами выполнения
- Решение систем дифференциальных уравнений
- Методы интегрирования систем дифференциальных уравнений
- Метод исключения
- Метод интегрируемых комбинаций
- Системы линейных дифференциальных уравнений
- Фундаментальная матрица
- Квадратная матрица
- Метод вариации постоянных
- Системы линейных дифференциальных уравнений с постоянными коэффициентами
- Метод Эйлера
- Матричный метод
- Понятие о системах дифференциальных уравнений
- 🔥 Видео
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Устойчивость решений ДУ по первому приближению
Пусть имеем систему дифференциальных уравнений
и пусть , есть точка покоя системы (1), т.е. . Будем предполагать, что функции дифференцируемы в начале координат достаточное число раз.
Разложим функции по формуле Тейлора по в окрестности начала координат:
здесь , а — члены второго порядка малости относительно .
Тогда исходная система (1) запишется так:
Вместо системы (2) рассмотрим систему
называемую системой уравнений первого приближения для системы (1).
Справедливы следующие предложения.
1. Если все корни характеристического уравнения
имеют отрицательные вещественные части , то нулевое решение , системы (3) и системы (2) асимптотически устойчивы .
2. Если хотя бы один корень характеристического уравнения (4) имеет положительную вещественную часть, то нулевое решение системы (3) и системы (2) неустойчиво .
Говорят, что в случаях 1 и 2 возможно исследование на устойчивость по первому приближению.
В критических случаях, когда вещественные части всех корней характеристического уравнения (4) неположительны, причем вещественная часть хотя бы одного корня равна нулю, исследование на устойчивость по первому приближению, вообще говоря, невозможно (начинают влиять нелинейные члены ).
Пример 1. Исследовать на устойчивость по первому приближению точку покоя системы
Решение. Системы первого приближения
Нелинейные члены удовлетворяют нужным условиям: их порядок больше или равен двум. Составим характеристическое уравнение для системы (6):
Корни характеристического уравнения (7) вещественные и 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADkAAAATBAMAAADYAbjmAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwB1kQYWh8DHg0VFNsKFOAAAA2ElEQVQoz2NgwA+YhbGLszSAqRwDrJJlkWBpHQFssuoGzEUgmvEQXIgjCc6MYWA4Crb4MEKHYwaMNZGBQRJEM51CMtBNBMo4yMAgA2bINCBJq0mDKSaQrAKIZRMA5CGkJ4OdDJJ1ADll+gQG1YUI3aqrkWUt204zKAWiyTJATWY+zXKMgQEhq7oYTBUyMIiDbDVgmK6AkFWDSDLkMDAANTED/RxjAJdVg/nIx4HlCAMDTwIw1ARgso4i8MgpNgeGPwfIcw5QWaSQZFA2QrAD8UVy43RhBpIBABPuJMc3pUukAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />. Следовательно, нулевое решение системы (5) неустойчиво.
Пример 2. Исследовать на устойчивость по первому приближению точку покоя систем
Решение. Точка покоя системы (8) асимптотически устойчива, так как для этой системы функция удовлетворяет всем условиям теоремы Ляпунова об асимптотической устойчивости. В частности,
В то же время точка покоя системы (9) неустойчива в силу теоремы Четаева: взяв , будем иметь .
Системы (8) и (9) имеют одну и ту же систему первого приближения
Характеристическое уравнение для системы (10)
имеет чисто мнимые корни, так что действительные части корней характеристического уравнения равны нулю.
Для системы первого приближения (10) начало координат является центром. Системы (8) и (9) получаются малым возмущением правых частей системы (10) в окрестности начала координат. Однако эти малые возмущения приводят к тому, что замкнутые траектории превращаются в спирали, в случае (8) приближающиеся к началу координат и образующие в точке устойчивый фокус, а в случае (9) — удаляющиеся от начала координат и образующие в точке неустойчивый фокус. Таким образом, в критическом случае нелинейные члены могут влиять на устойчивость точки покоя.
Пример 3. Рассмотрим замкнутый контур с линейными элементами (рис. 44); уравнение контура
Здесь — заряд конденсатора и, следовательно, — ток в цепи; — сопротивление; — индуктивность; — емкость; — нелинейные члены, имеющие степень не ниже второй, .
Решение. Уравнение (11) эквивалентно системе
для которой начало координат , есть точка покоя.
Рассмотрим систему первого приближения
Характеристическое уравнение для системы (13) имеет вид
Если , т.е. , то уравнение (14) имеет комплексные корни с отрицательной действительной частью и, значит, начало координат для системы (13) и (12) асимптотически устойчиво.
Если frac» png;base64,iVBORw0KGgoAAAANSUhEUgAAAFEAAAAsBAMAAADvHUkaAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAmIEBQRBl6MDRIDBRsUCjJh5DAAAB1ElEQVQ4y2NgoCIwNjYgQpUaAwPL////NxBUyPIJSBh9NCZsZDhIJccXIiwXBKm0LyaskOUKSKX/BcIqI0NAKvUTCKuUAfuon7DPuS+AVDJ/JxycFgtAKln+MjBwKSAJs+mhK2TOVFL8ocXABFTNhOzUOy8F0JUucXH76AoOznAkB3DX8PzGtN8EaJ79ZwbWiUhirN18/zAUsjr+OBoiX+cmDoklViUlJbUFQIeWYqjkUlLSegSUVoJ4iNX3x5HEj0C3HCAYGEzfGJjlE1i7CccExy8GBnkFxg27wdoO41EJSivzE2SVwIayaibjVukvwMD2l7ujowHibM1UnCr15fzEkWKLNVMVl8p+JfVq1FiUwq4QmFZYy9EiXBRELRREAqAgZAGGZT9KwmI+gakyARqc/w2IsR0YnCzIKplx+Yg5vtiA5T/rBLjX1XF53f///wus8xNheQUj5Jn3eDHsgjANgCUEyymYBCOaQlb1iZrapcQUXzunGDDcn0CEQu7KAAaG/QJEqAwHWWxPOOWC0i1IZQBhlVz/QYpYiLCc6S+xBTfHJ6JVgrNvArEquYgJJMZvQILXgQiVXOVAv4sR407m41OMPRKI8hKX+Hcp4jzPjKiKAKp5cVgk81juAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, то начало координат также асимптотически устойчиво (все параметры положительны).
Асимптотическая устойчивость точки покоя видна из физических соображений: при положительном омическом сопротивлении с возрастанием ток неизбежно исчезает.
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Устойчивость решений ДУ по отношению к изменению правых частей уравнений
Рассмотрим дифференциальные уравнения
где функции и непрерывны в замкнутой области плоскости и функция имеет в этой области непрерывную частную производную .
Пусть в области выполняется неравенство . Если и есть решения уравнений (1) и (2) соответственно, удовлетворяющие одному и тому же начальному условию , то
Из оценки (3) видно, что если возмущение правой части (1) достаточно мало в области , то на конечном интервале изменения разность решений уравнений (1) и (2) будет малой по абсолютной величине. Это позволяет приближенно решать сложные дифференциальные уравнения путем замены их разумно выбранными уравнениями, решаемыми проще. Последнее обстоятельство может быть использовано при решении дифференциальных уравнений, связанных с задачами физики или техники.
Пример 4. В квадрате найти приближенное решение уравнения
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Системы дифференциальных уравнений с примерами решения и образцами выполнения
Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.
Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Решение систем дифференциальных уравнений
К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 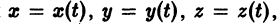
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 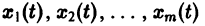
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
Если 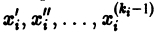
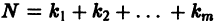
Например, одно уравнение
является мастным случаем канонической системы. Положив 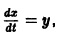
В результате получаем нормальную систему уравнений
эквивалентную исходному уравнению.
Определение:
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций
дифференцируемых на интервале а
Теорема:
Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений
и пусть функции 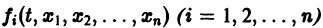
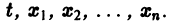

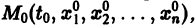

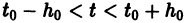
Определение:
Система n функций
зависящих от t и n произвольных постоянных 

1) при любых допустимых значениях 
2) в области 
Решения, получающиеся из общего при конкретных значениях постоянных 
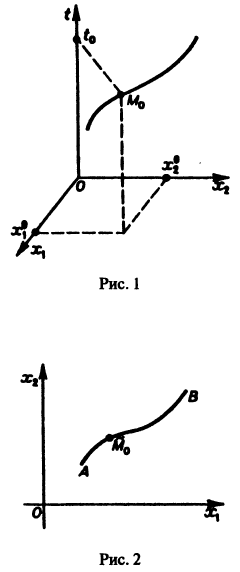
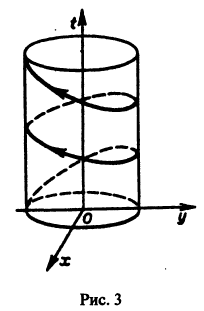
Обратимся для наглядности к нормальной системе двух уравнений,
Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 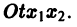
системы (7), принимающее при 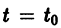
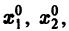
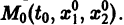
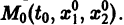
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение
системы — как параметрические уравнения кривой на плоскости 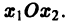
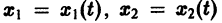
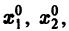
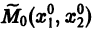
Методы интегрирования систем дифференциальных уравнений
Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной
Введя новые функции 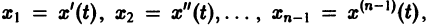
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему
Продифференцируем первое из уравнений (2) по t. Имеем
Заменяя в правой части производные 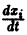
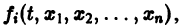
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим
Продолжая этот процесс, найдем
Предположим, что определитель
(якобиан системы функций 
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
будет разрешима относительно неизвестных 

Внося найденные выражения в уравнение
получим одно уравнение n-го порядка
Из самого способа его построения следует, что если 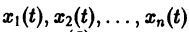
Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 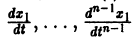
от t в систему уравнений
По предположению эту систему можно разрешить относительно 

Можно показать, что так построенная система функций
составляет решение системы дифференциальных уравнений (2). Пример:
Требуется проинтегрировать систему
Дифференцируя первое уравнение системы, имеем
откуда, используя второе уравнение, получаем
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид
В силу первого уравнения системы находим функцию
Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.
Функции x(t), y(t) можно представить в виде
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 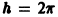
Исключая в формулах (7) параметр t, получаем уравнение
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.
При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.
Замечание:
Может оказаться, что функции 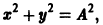
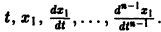
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример:
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:
Мы нашли два конечных уравнения
из которых легко определяется общее решение системы:
Одна интегрируемая комбинация дает возможность получить одно уравнение
связывающее независимую переменную t и неизвестные функции 
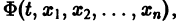
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций 
то задача интефирования системы (8) решена (так как из системы
определяются все неизвестные функции
Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
или, в матричной форме,
Теорема:
Если все функции 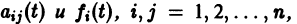
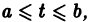
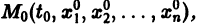
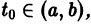
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, 
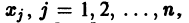
Введем линейный оператор
Тогда система (2) запишется в виде
Если матрица F — нулевая, т. е. 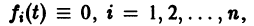
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема:
Если X(t) является решением линейной однородной системы
то cX(t), где с — произвольная постоянная, является решением той же системы.
Теорема:
двух решений 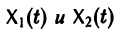
Следствие:
с произвольными постоянными коэффициентами сi решений 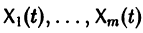
является решением той же системы.
Теорема:
Если 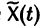
a Xo(t) — решение соответствующей однородной системы
будет решением неоднородной системы
Действительно, по условию,
Пользуясь свойством аддитивности оператора 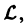
Это означает, что сумма 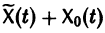
Определение:
называются линейно зависимыми на интервале a
при 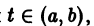

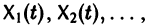
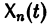
Заметим, что одно векторное тождество (5) эквивалентно n тождествам:
называется определителем Вронского системы векторов
Определение:
Пусть имеем линейную однородную систему
где 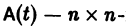
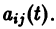
линейной однородной системы (6), линейно независимых на интервале а
с непрерывными на отрезке 
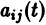
(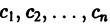
Пример:
имеет, как нетрудно проверить, решения
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
Общее решение системы имеет вид
(с1, с2 — произвольные постоянные).
Фундаментальная матрица
Квадратная матрица
столбцами которой являются линейно независимые решения 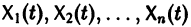
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем
Матрица 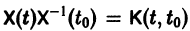
Теорема:
О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 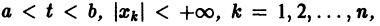
с непрерывными на отрезке 
соответствующей однородной системы и какого-нибудь частного решения 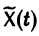
Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).
есть общее решение однородной системы (6), тогда
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
где 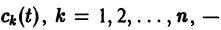
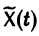
Подставляя 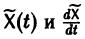
то для определения 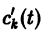
или, в развернутом виде,
Система (10) есть линейная алгебраическая система относительно 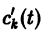
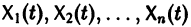
где 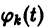
Подставляя эти значения 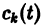
(здесь под символом 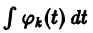
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
в которой все коэффициенты 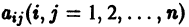
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Метод Эйлера
Будем искать решение системы
где 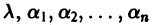
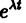
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 
Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно 


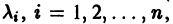
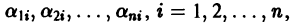
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид
где 
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример:
Ищем решение в виде
имеет корни
Система (3) для определения a1, а2 выглядит так:
Подставляя в (*) 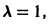
откуда а21 = а11. Следовательно,
Полагая в 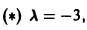
Общее решение данной системы:
Матричный метод
Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

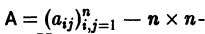
Напомним некоторые понятия из линейной алгебры. Вектор 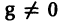
Число 
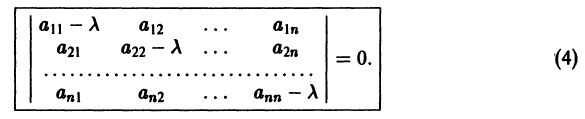
где I — единичная матрица.
Будем предполагать, что все собственные значения 
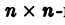
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.
Введем еще следующие понятия. Пусть В(t) — 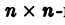








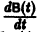
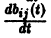
Пусть B(t) — n х n-матрица,
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы
В частности, если В — постоянная матрица, то
так как 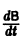
Теорема:
Если собственные значения 
где g1, g2,…, gn — собственные векторы-столбцы матрицы А, 
Введем новый неизвестный вектор-столбец Y(t) по формуле
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему
Умножая обе части последнего соотношения слева на 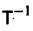
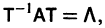
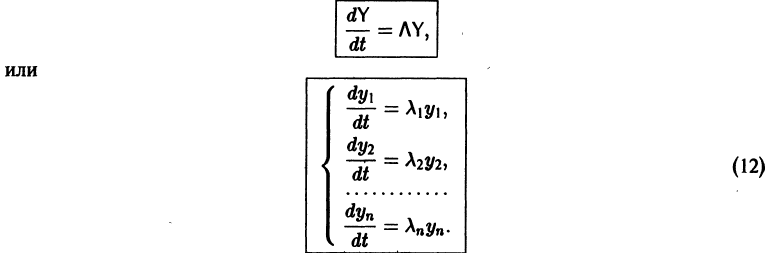
Мы получили систему из n независимых уравнений, которая без труда интегрируется:
Здесь 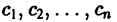
Вводя единичные n-мерные векторы-столбцы
решение Y(t) можно представить в виде
В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 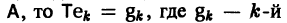
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения 
2) находим все собственные векторы g1, g2,…, gn;
3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).
Пример:
Матрица А системы имеет вид
1) Составляем характеристическое уравнение
Корни характеристического уравнения
2) Находим собственные векторы
Для 
откуда g11 = g12, так что
Аналогично для 
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 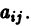
будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем 




При комплексном 
системы (7) также будет комплексным. Действительная часть
этого решения являются решениями системы (7). Собственному значению 



Пусть 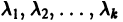
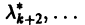
где сi — произвольные постоянные.
Пример:
1) Характеристическое уравнение системы
Его корни
2) Собственные векторы матриц
3) Решение системы
где а1, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
Следовательно, всякое действительное решение системы имеет
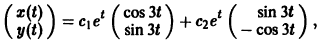
где с1, с2 — произвольные действительные числа.
Видео:Системы дифференциальных уравненийСкачать

Понятие о системах дифференциальных уравнений




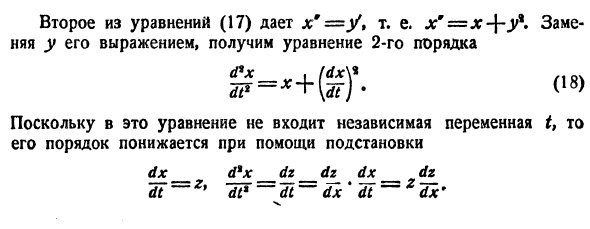

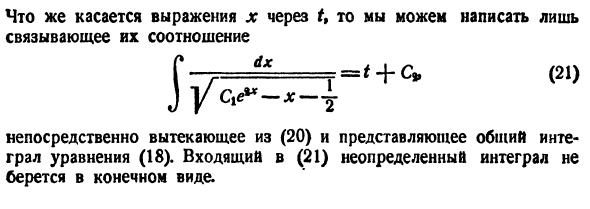

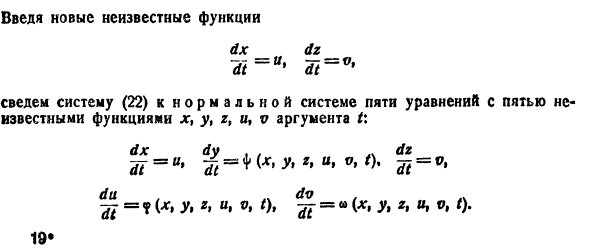
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🔥 Видео
Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Системы дифференциальных уравнений. Часть 2Скачать

Линейные системы дифференциальных уравненийСкачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Устойчивость 5 Устойчивость по первому приближению Теорема ПримерыСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать