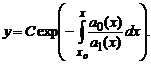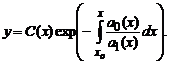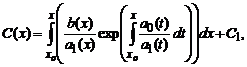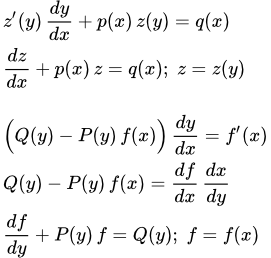Линейное дифференциальное уравнение относительно x

Назначение сервиса . Онлайн калькулятор можно использовать для проверки решения однородных и неоднородных линейных дифференциальных уравнений вида y’+y=b(x) .

• Решение онлайн
• Видеоинструкция

Теорема. Пусть a₁(x) , a₀(x) , b(x) непрерывны на отрезке [α,β], a₁≠0 для ∀x∈[α,β]. Тогда для любой точки (x₀, y₀), x₀∈[α,β], существует единственное решение уравнения, удовлетворяющее условию y(x₀) = y₀ и определенное на всем интервале [α,β].
Рассмотрим однородное линейное дифференциальное уравнение a₁(x)y’+a₀(x)y=0 .
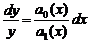
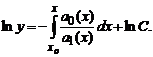
Разделяя переменные, получаем , или, интегрируя обе части, Последнее соотношение, с учетом обозначения exp(x) = e x , записывается в форме

Попытаемся теперь найти решение уравнения в указанном виде, в котором вместо константы C подставлена функция C(x) то есть в виде

Подставив это решение в исходное, после необходимых преобразований получаем 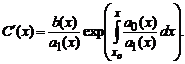Интегрируя последнее, имеем

где C₁— некоторая новая константа. Подставляя полученное выражение для C(x), окончательно получаем решение исходного линейного уравнения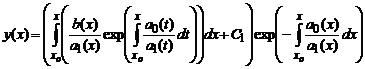
.

Описанный метод решения называется методом Лагранжа или методом вариации произвольной постоянной (см. также Метод вариации произвольной постоянной решения линейных неоднородных уравнений).

Пример . Решить уравнение y’ + 2y = 4x . Рассмотрим соответствующее однородное уравнение y’ + 2y = 0 . Решая его, получаем y = Ce -2 x . Ищем теперь решение исходного уравнения в виде y = C(x)e -2 x . Подставляя y и y’ = C'(x)e -2 x — 2C(x)e -2 x в исходное уравнение, имеем C'(x) = 4xe 2 x , откуда C(x) = 2xe 2 x — e 2 x + C₁ и y(x) = (2xe 2 x — e 2 x + C₁)e -2 x = 2x — 1 + C₁e -2 x — общее решение исходного уравнения. В этом решении y₁(x) = 2x-1 — движение объекта под действием силы b(x) = 4x, y₂(x) = C₁e -2 x -собственное движение объекта.

Пример №2 . Найти общее решение дифференциального уравнения первого порядка y’+3 y tan(3x)=2 cos(3x)/sin 2 2x.
Это неоднородное уравнение. Сделаем замену переменных: y=u•v, y’ = u’v + uv’.
3u v tg(3x)+u v’+u’ v = 2cos(3x)/sin 2 2x или u(3v tg(3x)+v’) + u’ v= 2cos(3x)/sin 2 2x
Решение состоит из двух этапов:
1. u(3v tg(3x)+v’) = 0
2. u’v = 2cos(3x)/sin 2 2x
1. Приравниваем u=0, находим решение для 3v tg(3x)+v’ = 0
Представим в виде: v’ = -3v tg(3x)

Интегирируя, получаем:

ln(v) = ln(cos(3x))
v = cos(3x)
2. Зная v, Находим u из условия: u’v = 2cos(3x)/sin 2 2x
u’ cos(3x) = 2cos(3x)/sin 2 2x
u’ = 2/sin 2 2x
Интегирируя, получаем:
Из условия y=u•v, получаем:
y = u•v = (C-cos(2x)/sin(2x)) cos(3x) или y = C cos(3x)-cos(2x) ctg(3x)

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Дифференциальные уравнения первого порядка, приводящиеся к линейным

Видео:Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Метод решения

К линейным уравнениям первого порядка приводится уравнения вида:
(1) ,
где z – функция от y ; p и q – функции от x .
Действительно, по правилу дифференцирования сложной функции:
.
Подставляя в (1), получаем уравнение, линейное относительно z :
.

Видео:8. Дифференциальные уравнения, линейные относительно х и х'Скачать

Дифференциальные уравнения, линейные относительно переменной x

Ранее мы рассматривали уравнения, линейные относительно переменной y . То есть мы считали, что x является независимой переменной, а y является зависимой переменной. Однако, всегда стоит иметь в виду, что возможен противоположный подход. То есть можно считать переменную y независимой переменной, а x – зависимой переменной. На практике часто встречаются задачи, в которых уравнение линейно относительно переменной x , а не y . В общем виде такое уравнение можно записать так:
(2) ,
где P, Q, R –функции от y .

Покажем, что это уравнение линейно относительно переменной x . Для этого выполняем преобразования. Представим производную в виде отношения дифференциалов:
.
Тогда уравнение (2) примет вид:
.
Умножаем на и выполняем алгебраические преобразования:
;
.
Разделив на R ( y ) , приводим уравнение к виду:
,
где .
Это – линейное относительно x дифференциальное уравнение.

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Пример решения дифференциального уравнения, приводящегося к линейному уравнению первого порядка

Решить уравнение:
(П.1) .

Подставим в (П.1):
.
Считаем, что y – это независимая переменная, а x – зависимая. То есть x – это функция от y . Умножим на :
(П.2) .
Делаем подстановку:
.
Здесь z – сложная функция от y , .
Дифференцируем по y . По правилу дифференцирования сложной функции:
.
Подставляем в (П.2):
;
.
Это линейное, относительно z , дифференциальное уравнение. Решаем его с помощью интегрирующего множителя. Умножаем уравнение на интегрирующий множитель e y :
;
;
.
Интегрируем по частям:

;

;
;
.
Переходим к переменной x :
;
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 05-08-2012 Изменено: 26-06-2015

Видео:Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

🎦 Видео

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Курс по ОДУ: Уравнения, не разрешённые относительно производной | Занятие 7Скачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения высших порядков, допускающие понижение порядкаСкачать

Линейное неоднородное дифференциальное уравнение 2 способаСкачать

#Дифуры I. Урок 4. Линейные дифференциальные уравнения. Метод вариации произвольной постояннойСкачать

Дифференциальные уравнения не разрешенные относительно производной | poporyadku.schoolСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Jah Khalib, Maruv - По льду (Текст/лирик)Скачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать