Линейно зависимые и линейно независимые системы уравнений

Видео:Линейная зависимость и линейная независимость векторов.Скачать

Линейная зависимость и независимость векторов

Набор векторов называется системой векторов .

Система из векторов называется линейно зависимой , если существуют такие числа , не все равные нулю одновременно, что

Система из векторов называется линейно независимой, если равенство (1.1) возможно только при , т.е. когда линейная комбинация в левой части равенства (1.1) тривиальная.

1. Один вектор тоже образует систему: при — линейно зависимую, а при — линейно независимую.

2. Любая часть системы векторов называется подсистемой .

Видео:Линейная зависимость и линейная независимость. ТемаСкачать

Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора , то она линейно зависима.

4. Система из 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAiXFYMbEhAcBBoPDQoeAQ0I3cqgAAALZJREFUKM+VktsSwyAIRDWKiFf+/2uLSZvEhkxaXnTGs7KsGvN3UYrwC+ffa3D8zCMlxo+QlyfcNmg7v7A/t7VBux/jzkOe54lJURw8ZrHvop0UdM8P+3axGc89aqQ7XuxbjzybMkEUqPLAIPP6/u0g1OYUHnMpTQs02KLxq/0p0Y1O0al+RvqOCcv51CeZF1UeJBjhacoT6PJehTd9k/R7gdgPul7ei3itcWeYPp/sqv4fRhnzAuOaBpbDogV3AAAAAElFTkSuQmCC» /> векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов линейно независима, а после присоединения к ней вектора оказывается линейно зависимой, то вектор можно разложить по векторам , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

Докажем, например, последнее свойство. Так как система векторов — линейно зависима, то существуют числа , не все равные 0, что . В этом равенстве . В самом деле, если , то . Значит, нетривиальная линейная комбинация векторов равна нулевому вектору, что противоречит линейной независимости системы . Следовательно, и тогда , т.е. вектор есть линейная комбинация векторов . Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения и , причем не все коэффициенты разложений соответственно равны между собой (например, ).

Тогда из равенства получаем .

Следовательно, линейная комбинация векторов равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере ), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов . Полученное противоречие подтверждает единственность разложения.

Пример 1.3. Параллелограмм построен на векторах и ; точки и — середины сторон и соответственно (рис. 1.11). Требуется:

а) найти линейные комбинации векторов

б) доказать, что векторы , , линейно зависимы.

а) Так как , то по правилу треугольника: .

Рассуждая аналогично, получаем: . Построим вектор . Из равенства треугольников и следует, что . Тогда .

б) Учитывая, что и , получаем: .

Перенося векторы в левую часть, приходим к равенству , т.е. нетривиальная линейная комбинация векторов , , равна нулевому вектору. Следовательно, векторы , , линейно зависимы, что и требовалось доказать.

Видео:Линейная зависимость векторовСкачать

Линейно зависимые и линейно независимые вектора.

Определение. Линейной комбинацией векторов a ₁, . a_n с коэффициентами x ₁, . x_n называется вектор

Видео:Линейная зависимость векторов. РангСкачать

Свойства линейно зависимых векторов:

Видео:Линейная зависимость строк и определитель матрицыСкачать

Примеры задач на линейную зависимость и линейную независимость векторов:

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

Это векторное уравнение можно записать в виде системы линейных уравнений

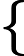	x 1 + x 2 = 0
	x 1 + 2 x 2 — x 3 = 0
	x 1 + x 3 = 0

Решим эту систему используя метод Гаусса

1 1 0 0 1 2 -1 0 1 0 1 0

из второй строки вычтем первую; из третей строки вычтем первую:

1 1 0 0 1 — 1 2 — 1 -1 — 0 0 — 0 1 — 1 0 — 1 1 — 0 0 — 0

1 1 0 0 0 1 -1 0 0 -1 1 0

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 0 1 — 1 0 — (-1) 0 — 0 0 1 -1 0 0 + 0 -1 + 1 1 + (-1) 0 + 0

1 0 1 0 0 1 -1 0 0 0 0 0

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x ₁, x ₂, x ₃ таких, что линейная комбинация векторов a , b , c равна нулевому вектору, например:

а это значит вектора a , b , c линейно зависимы.

Ответ: вектора a , b , c линейно зависимы.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

Это векторное уравнение можно записать в виде системы линейных уравнений

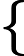	x 1 + x 2 = 0
	x 1 + 2 x 2 — x 3 = 0
	x 1 + 2 x 3 = 0

Решим эту систему используя метод Гаусса

1 1 0 0 1 2 -1 0 1 0 2 0

из второй строки вычтем первую; из третей строки вычтем первую:

1 1 0 0 1 — 1 2 — 1 -1 — 0 0 — 0 1 — 1 0 — 1 2 — 0 0 — 0

1 1 0 0 0 1 -1 0 0 -1 2 0

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 0 1 — 1 0 — (-1) 0 — 0 0 1 -1 0 0 + 0 -1 + 1 2 + (-1) 0 + 0

1 0 1 0 0 1 -1 0 0 0 1 0

из первой строки вычтем третью; к второй строке добавим третью:

1 — 0 0 — 0 1 — 1 0 — 0 0 + 0 1 + 0 -1 + 1 0 + 0 0 0 1 0

1 0 1 0 0 1 0 0 0 0 1 0

Данное решение показывает, что система имеет единственное решение x ₁ = 0, x ₂ = 0, x ₃ = 0, а это значит вектора a , b , c линейно независимые.

Ответ: вектора a , b , c линейно независимые.

Видео:Линейная зависимость и независимость систем векторовСкачать

Линейно зависимые и линейно независимые функции. Примеры исследования функций на линейную зависимость по определению.

Функции $y_1(x),;y_2(x),;y_3(x),ldots,y_n(x)$ называются линейно зависимыми на некотором множестве $T$, если существуют такие константы $alpha_1,;alpha_2,;alpha_3,ldots,alpha_n$, что $forall xin T$ выполняется следующее равенство:

$$ begin alpha_1cdot y_1+alpha_2cdot y_2+ldots+alpha_ncdot y_n=0 end $$

Примечание к терминологии: показатьскрыть

В определении использован термин «равенство», хотя можно было бы воспользоваться термином «тождество». Фразы «для каждого значения переменной $xin T$ выполняется равенство $a(x)=b(x)$» и «на множестве $T$ верно тождество $a(x)equiv b(x)$» равносильны. Например, фраза «равенство $sin^2x=1-cos^2x$ выполнено для $forall xin R$», равносильна такой: «на множестве $R$ верно тождество $sin^2x=1-cos^2x$». Т.е. вместо слов о том, что «$forall xin T$ выполняется следующее равенство: $alpha_1cdot y_1+alpha_2cdot y_2+ldots+alpha_ncdot y_n=0$» можно сказать так: «на множестве $T$ верно тождество $alpha_1cdot y_1+alpha_2cdot y_2+ldots+alpha_ncdot y_nequiv 0$». Некоторые авторы предпочитают использовать именно термин «тождество».

Условие (2) можно изложить и в такой формулировке: среди коэффициентов $alpha_i$ есть хотя бы один, не равный нулю.

Несложно убедиться в равносильности формулировок. Равенство $alpha_^+alpha_^+ldots+alpha_^=0$ возможно в том и только в том случае, когда $alpha_1=alpha_2=ldots=alpha_n=0$. Если же $sum_^alpha_^neq 0$, то равенство $alpha_1=alpha_2=ldots=alpha_n=0$ не выполнено, т.е. хотя бы один из коэффициентов $alpha_i$ отличен от нуля.

Если же равенство (1) возможно лишь при условии:

то функции $y_1(x),;y_2(x),;y_3(x),ldots,y_n(x)$ именуют линейно независимыми на множестве $T$. По сути, условие (3) равносильно такому: все коэффициенты $alpha_i$ равны нулю.

Для двух функций несложно вывести простое правило: если $forall xin T$ $fracneq const$ на некотором интервале $T=(a;b)$, то функции $y_1(x)$ и $y_2 (x)$ линейно независимы на $T$. Если же $forall xin T$ $frac= const$ на $T$, то функции $y_1(x)$ и $y_2 (x)$ линейно зависимы на $T$.

Обоснование этого правила: показатьскрыть

Допустим, что $fracneq const$ на $T$, однако функции $y_1(x)$ и $y_2 (x)$ линейно зависимы. Если функции линейно зависимы, то существуют такие константы $alpha_1$ и $alpha_2$, не равные нулю одновременно, что выполняется равенство: $alpha_1cdot y_1+alpha_2cdot y_2=0$. Пусть, к примеру, $alpha_1neq 0$. Тогда, с учетом $y_2 (x)neq 0$ на $T$, получим: $frac=-frac=const$, что противоречит допущению $fracneq const$.

Если же $frac= const$, то $y_1(x)-Ccdot y_2(x)=0$ на $T$, т.е. $alpha_1=1;;alpha_2=-C$. При этом $alpha_^+alpha_^=1+C^2neq 0$, т.е. функции $y_1(x)$ и $y_2 (x)$ линейно зависимы на $T$.

Все примеры, указанные в этой теме, будут опираться на определения и свойство, приведенные выше. Естественно, что в общем случае применение таких определений несколько затруднительно. Существует несколько критериев, которые позволяют упростить процесс проверки функций на линейную зависимость. На сайте рассмотрены два таких способа: с помощью определителя Вронского и определителя Грама.

Выяснить, являются ли функции $y_1(x)=x^2+2x-4$, $y_2(x)=-4x^2+7x-1$, $y_3(x)=-5x^2+20x-14$ линейно зависимыми или линейно независимыми на множестве $R$.

Рассмотрим линейную комбинацию этих функций: $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3$. Если $forall xin R$ равенство $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ выполняется только при $alpha_1=alpha_2=alpha_3=0$, то рассматриваемые функции линейно независимы. Если же $forall xin R$ равенство $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ возможно при условии, что хотя бы один из коэффициентов $alpha_i$ не равен нулю, то функции линейно зависимы.

Подставим в выражение $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ заданные функции:

Раскроем скобки и перегруппируем слагаемые:

$$ alpha_1cdot x^2+2alpha_1cdot x-4alpha_1-4alpha_2cdot x^2+7alpha_2cdot x-alpha_2-5alpha_3cdot x^2+20alpha_3cdot x-14alpha_3=0; $$ $$(alpha_1-4alpha_2-5alpha_3)cdot x^2+(2alpha_1+7alpha_2+20alpha_3)cdot x+(-4alpha_1-alpha_2-14alpha_3)=0.$$

Последнее равенство возможно лишь в том случае, когда коэффициенты при степенях переменной $x$ одновременно равны нулю, т.е.:

Мы получили однородную систему линейных уравнений. Нам нет необходимости в её решении, нужно лишь установить количество решений. Если решение лишь одно – нулевое (или, в иной терминологии, тривиальное), т.е. $alpha_1=alpha_2=alpha_3=0$, то функции линейно независимы. Если же есть иные решения, кроме нулевого, то функции линейно зависимы. Найдем ранг матрицы системы $A= left( begin 1 & -4& -5\ 2 & 7& 20 \ -4& -1& -14 end right)$ и ранг расширенной матрицы системы: $tilde= left( begin 1 & -4& -5& 0\ 2 & 7& 20 & 0 \ -4& -1& -14 & 0 end right)$, а затем применим теорему Кронекера-Капелли.

Отсюда получаем решение: $left< begin&alpha_1=-3alpha_3;\&alpha_2=-2alpha_3;\&alpha_3=alpha_3;;alpha_3 in R end right.$ Например, подставив $alpha_3=-1$, получим: $alpha_1=3;; alpha_2=2$. Несложно убедиться непосредственной проверкой, что равенство $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ при найденных коэффициентах будет выполнено $forall xin R$:

$$ 3cdot y_1+2cdot y_2-y_3=3cdot(x^2+2x-4)+2cdot(-4x^2+7x-1)-(-5x^2+20x-14)=0. $$

Итак, существуют такие константы $alpha_1;;alpha_2;;alpha_3$ (например, $alpha_1=3;;alpha_2=2;;alpha_3=-1$), не все одновременно равные нулю, что на $R$ выполняется тождество $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3equiv 0$. Следовательно, рассматриваемые функции линейно зависимы.

Исследовать на линейную зависимость такие функции: $y_1(x)=xln(x+4);;y_2(x)=ln^2(x+4)$.

Исследование проведем в интервале $T=(-4;+infty)$, который представляет собой область определения заданных функций. Применим правило для определения линейной зависимости двух функций, указанное в начале страницы. Так как при $xin(-4;+infty)$ имеем: $frac=fracneq const$, то данные функции линейно независимы на $T=(-4;+infty)$.

Исследовать на линейную зависимость функции: $y_1(x)=1$, $y_2(x)=x$, $y_3(x)=x^2$, $y_4(x)=x^3$, $y_5(x)=x^4$.

Область определения этих функций есть вся числовая прямая, т.е. $x in R$. Рассмотрим равенство:

$$ begin alpha_1cdot 1+alpha_2cdot x+alpha_3cdot x^2+alpha_4cdot x^3+alpha_5cdot x^4=0 end $$

Если равенство (4) для всех $xin R$ возможно лишь при условии $alpha_1=alpha_2=alpha_3=alpha_4=alpha_5=0$, то заданные функции линейно независимы. Если же равенство (4) $forall xin R$ выполняется на наборе констант $alpha_1$, $alpha_2$, $alpha_3$, $alpha_4$, $alpha_5$, среди которых хотя бы одна отлична от нуля, то заданные функции линейно зависимы. Итак, нужно исследовать равенство (4).

В левой части равенства (4) расположен многочлен, порядок (или, в иной терминологии, степень) которого не превышает $4$. Например, если $alpha_1=2; ;alpha_2=0;;alpha_3=0;;alpha_4=7;;alpha_5=0$, то получим многочлен третьего порядка:

$$alpha_1cdot 1+alpha_2cdot x+alpha_3cdot x^2+alpha_4cdot x^3+alpha_5cdot x^4=7x^3+2.$$

Т.е. в левой части равенства (4) может быть многочлен четвертого, третьего, второго, первого и нулевого порядков.

Рассмотрим случай, когда в левой части равенства (4) расположен многочлен, порядок которого не равен нулю (среди констант $alpha_2;;alpha_3;;alpha_4;;alpha_5$ хотя бы одна не равна нулю). Любой многочлен первого порядка может обратиться в ноль только в одной точке (т.е. существует только одно значение $x$, при котором многочлен первого порядка равен нулю). Многочлен второго порядка равен нулю не более, чем в двух точках; многочлен третьего порядка – не более, чем в трёх точках; многочлен четвертого порядка обращается в ноль не более, чем в четырёх точках. Т.е. если среди констант $alpha_2;;alpha_3;;alpha_4;;alpha_5$ есть хотя бы одна, отличная от нуля, то равенство (4) может быть выполнено не более, чем при четырёх значениях $x$ (а не для всех $xin R$).

Рассмотрим ситуацию, когда среди констант $alpha_2;;alpha_3;;alpha_4;;alpha_5$ нет ни одной, отличной от нуля, т.е. $alpha_2=alpha_3=alpha_4=alpha_5=0$. В этом случае в левой части равенства (4) получим многочлен нулевого порядка:

$$alpha_1cdot 1+alpha_2cdot x+alpha_3cdot x^2+alpha_4cdot x^3+alpha_5cdot x^4=alpha_1$$

А само равенство (4) станет таким: $alpha_1=0$. Следовательно, для многочлена нулевого порядка выполнение равенства (4) возможно лишь при $alpha_1=alpha_2=alpha_3=alpha_4=alpha_5=0$.

Подведём итоги: если в правой части равенства (4) стоит многочлен ненулевого порядка, то равенство (4) не может быть выполнено при всех $xin R$. Равенство (4) может быть выполнено для всех $xin R$ только когда в правой части стоит многочлен нулевого порядка, однако это означает $alpha_1=alpha_2=alpha_3=alpha_4=alpha_5=0$. Так как равенство (4) выполняется для всех $xin R$ только при условии $alpha_1=alpha_2=alpha_3=alpha_4=alpha_5=0$, то заданные функции линейно независимы на $R$.

Исследовать на линейную зависимость функции: $y_1(x)=4$, $y_2(x)=arcsin$, $y_3(x)=arccos$ на отрезке $[-1;1]$.

Так как $arcsin x+arccos x=frac ; forall x in [-1;1]$ то:

$$arcsin x+arccos x=fraccdot4; ; arcsin x+arccos x-fraccdot4=0; ; 1cdot y_1+1cdot y_2+left(-fracright)cdot y_3=0$$

Итак, существует такой набор констант $alpha_1; ; alpha_2;; alpha_3$ (например, $alpha_1=1;; alpha_2=1;; alpha_3=-frac$), среди которых есть хотя бы одна константа, отличная от нуля, что равенство $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ будет выполнено для всех $xin[-1;1]$. Это означает, что функции $y_1(x)=4$, $y_2(x)=arcsin$, $y_3(x)=arccos$ линейно зависимы на отрезке $[-1;1]$.

Исследовать на линейную зависимость функции: $y_1(x)=x;; y_2(x)=|x|$ в их области определения.

Областью определения заданных функций есть все множество действительных чисел, т.е. $xin R$. Функции будут линейно зависимыми, если существует такой набор констант $alpha_1$ и $alpha_2$, что для всех значений $xin R$ выполнено равенство $alpha_1cdot y_1+alpha_2cdot y_2=0$ (т.е. $alpha_1cdot x+alpha_2cdot |x|=0$), причем хотя бы один из коэффициентов ($alpha_1$ или $alpha_2$) не равен нулю. Если же выполнение равенства $alpha_1cdot y_1+alpha_2cdot y_2=0$ при $forall xin R$ возможно лишь при $alpha_1=alpha_2=0$, то заданные функции будут линейно независимыми. Рассмотрим равенство $alpha_1cdot x+alpha_2cdot |x|=0$ подробнее.

Если $x≥ 0$, то $|x|=x$, поэтому равенство $alpha_1cdot x+alpha_2cdot |x|=0$ станет таким: $alpha_1cdot x+alpha_2cdot x=0$, $xcdot(alpha_1+alpha_2)=0$. Равенство $xcdot(alpha_1+alpha_2)=0$ должно быть выполнено при всех $x≥ 0$, поэтому $alpha_1+alpha_2=0$.

Итак, чтобы равенство $alpha_1cdot x+alpha_2cdot |x|=0$ было верным для всех $xin R$, требуется выполнение двух условий:

Полученная система имеет лишь тривиальное (нулевое) решение: $alpha_1=alpha_2=0$. Итак, выполнение равенства $alpha_1cdot x+alpha_2cdot |x|=0$ при $forall xin R$ возможно лишь в случае $alpha_1=alpha_2=0$, поэтому функции линейно независимы на R.

Исследование на линейную зависимость с помощью определителей Вронского и Грама указаны в дальнейших темах сайта.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

🎥 Видео

Линейно зависимые векторы: как доказать?Скачать

Линейная комбинация. Линейная зависимость (независимость) матриц.Скачать

Практика 10 Линейная зависимость функцийСкачать

Овчинников А. В. - Аналитическая геометрия - Линейно зависимые и линейно независимые векторыСкачать

Линейная зависимость векторов на примерахСкачать

Примеры линейной зависимости векторов.Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Линейная алгебра, 6 урок, Ранг матрицыСкачать

Линейная зависимость и линейная независимость строк столбцов матрицы. Часть 1.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Линейная зависимость векторов. Линейная алгебра. Лекция 2Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Линейная зависимость и независимость векторов. Базис.Скачать

§44 Линейная независимость векторовСкачать