Линейная зависимость и системы линейных уравнений связь ранга матрицы с базисом системы векторов

Видео:Примеры Линейная зависимость векторов Базис и ранг системы векторовСкачать

Определение.

Мы будем называть матрицей размеров (m times n) совокупность (mn) чисел, расположенных в виде таблицы из (m) строк и (n) столбцов:
$$
begin
a_^& a_^& ldots & a_^\
a_^& a_^& ldots & a_^\
ldots&ldots&ldots&ldots\
a_^& a_^& ldots& a_^
endnonumber
$$
Числа, составляющие матрицу, мы будем называть элементами матрицы. Если число строк в матрице равно числу столбцов, то матрица называется квадратной, а число строк — её порядком. Остальные матрицы носят название прямоугольных.

Можно дать и такое определение матрицы. Рассмотрим два множества целых чисел (I=) и (J=). Через (I times J) обозначим множество всех пар вида ((i, j)), где (i in I), a (j in J). Матрицей называется числовая функция на (I times J), то есть закон, сопоставляющий каждой паре ((i, j)) некоторое число (a_^).

Для читателя, знакомого с программированием, заметим, что матрица — это в точности то же, что и двумерный массив.

Две матрицы называются равными, если они имеют одинаковые размеры, и равны их элементы, стоящие на одинаковых местах.

Рассматривая произвольные матрицы, мы будем обозначать их элементы буквами с двумя индексами. Если оба индекса расположены внизу, то первый из них обозначает номер строки, а второй — номер столбца; если один из индексов расположен сверху, как в написанной выше матрице, то этот индекс обозначает номер строки. Не следует путать верхние индексы с показателями степени.

Матрицу размеров (1 times n), состоящую из одной строки, мы будем называть строкой длины (n) или просто строкой. Матрицу размеров (m times 1) называют столбцом высоты (m) или просто столбцом. Столбцы и строки мы будем обозначать полужирными буквами.

Рассмотрим матрицу (A) размеров (m times n) и выберем какие-нибудь (r) номеров строк (i_, ldots, i_) и (s) номеров столбцов (j_, ldots, j_), причем будем предполагать, что номера выбраны в порядке возрастания: (i_ Определение.

Матрица (A) называется симметричной или симметрической, если (A^=A). Для такой матрицы (a_=a_) при всех (i) и (j) — элементы, расположенные симметрично относительно главной диагонали, равны.

Матрица (A) называется кососимметричной или антисимметричной, если (A^=-A). Для такой матрицы (a_=-a_) при всех (i) и (j) — элементы, расположенные симметрично относительно главной диагонали, отличаются знаком. Диагональные элементы равны нулю.

Матрица (A) называется верхней треугольной, если ее элементы, расположенные ниже главной диагонали, равны нулю: (a_=0) при (i > j). Аналогично определяется нижняя треугольная матрица: (a_=0) при (i Определение.

Матрица (A) называется диагональной, если у нее равны нулю все недиагональные элементы: (a_=0) при (i neq j).

Другие частные виды матриц будем определять по мере необходимости.

Видео:Линейная зависимость и линейная независимость векторов.Скачать

Сложение и умножение на число.

Пусть (A) и (B) — матрицы размеров (m times n). Мы можем сопоставить им третью матрицу (C) размеров (m times n), элементы которой (c_) связаны с элементами и матриц (A) и (B) равенствами
$$
c_=a_+b_ (i=1, ldots, m, j=1, ldots, n).label
$$

Матрица (C), определяемая по (A) и (B) формулой eqref, называется их суммой и обозначается (A+B).

Матрица (C), элементы которой (c_) равны произведениям элементов (a_) матрицы (A) на число (alpha), называется произведением (A) на (alpha) и обозначается (alpha A). Мы имеем
$$
c_=alpha a_ (i=1, ldots, m, j=1, ldots, n).label
$$

Из свойств сложения и умножения чисел легко вытекает наше первое утверждение.

Для любых матриц (A, B, C) и любых чисел (alpha) и (beta) выполнены равенства:

Матрица, все элементы которой равны нулю, называется нулевой матрицей. Если (O) — нулевая матрица размеров (m times n), то для любой матрицы тех же размеров
$$
A+O=A.nonumber
$$

Матрицу ((-1)A) называют противоположной матрице (A) и обозначают (-A). Она обладает тем свойством, что
$$
A+(-A)=O.nonumber
$$

Сумма матриц (B) и (-A) называется разностью матриц (B) и (A) и обозначается (B-A). Мы видим, что сформулированные выше свойства линейных операций с матрицами совпадают со свойствами линейных операций с векторами. Используя линейные операции, мы можем составлять из матриц одинаковых размеров (A_, ldots, A_) и чисел (alpha_, ldots, alpha_), выражения вида
$$
alpha_A_+ldots+alpha_A_.nonumber
$$

Такие выражения называются линейными комбинациями матриц. Если какая-то матрица представлена как линейная комбинация других матриц, то говорят, что она по ним разложена.

Пусть (boldsymbol

_, ldots, boldsymbol

_), — столбцы одинаковой высоты (n). Тогда столбец (boldsymbol) той же высоты по ним разложен, если при некоторых коэффициентах (alpha_, ldots, alpha_)
$$
boldsymbol=alpha_boldsymbol

_+ldots+alpha_boldsymbol

_,nonumber
$$
или, в более подробной записи,
$$
begin q^\
vdots\
q^
end=alpha_
begin p_^\
vdots\
p_^ end+ldots+alpha_ begin p_^\
vdots\
p_^ end.nonumber
$$
В силу определения линейных операций это матричное равенство равносильно (n) числовым равенствам
$$
begin
q^=alpha_p_^+ldots+alpha_p_^,\
ldots\
q^=alpha_p_^+ldots+alpha_p_^.
endnonumber
$$

Видео:Линейная зависимость векторов. РангСкачать

Линейная зависимость матриц.

Какова бы ни была система матриц фиксированных размеров (m times n), нулевая матрица тех же размеров раскладывается по этим матрицам в линейную комбинацию с нулевыми коэффициентами. Такую линейную комбинацию называют тривиальной. Как и для векторов, введем понятие линейной независимости.

Система матриц (A_, ldots, A_) линейно независима, если нулевая матрица раскладывается по ней однозначно, то есть из
$$
alpha_A_+ldots+alpha_A_=O.label
$$
следует (alpha_=ldots=alpha_=0).

В противном случае, то есть если существуют (k) чисел (alpha_, ldots, alpha_), одновременно не равных нулю и таких, что выполнено равенство eqref(3), система матриц называется линейно зависимой.

Столбцы
$$
boldsymbol_=begin 1\ 0\ vdots\ 0 end, boldsymbol_=begin 0\ 1\ vdots\ 0 end, ldots, boldsymbol_=begin 0\ 0\ vdots\ 1 endlabel
$$
(в столбце (boldsymbol_) на (i)-м месте стоит 1, а остальные элементы равны нулю) являются линейно независимыми. Действительно, равенство (alpha_boldsymbol_+ldots+alpha_boldsymbol_=boldsymbol) можно записать подробнее так:
$$
alpha_ begin 1\ 0\ vdots\ 0 end+alpha_ begin 0\ 1\ vdots\ 0 end+ldots+alpha_ begin 0\ 0\ vdots\ 1 end=begin alpha_\ alpha_\ vdots\ alpha_ end=begin 0\ 0\ vdots\ 0 end.nonumber
$$
Отсюда видно, что (alpha_=alpha_=ldots=alpha_=0).

Это равенство показывает также, что произвольный столбец высоты (n) может быть разложен по столбцам (boldsymbol_, ldots, boldsymbol_). Действительно, в качестве коэффициентов линейной комбинации нужно взять элементы раскладываемого столбца.

Квадратная матрица порядка (n), состоящая из столбцов eqref:
$$
E=begin
1& 0& ldots& 0\
0& 1& ldots& 0\
ldots&ldots&ldots&ldots\
0& 0& ldots& 1 end,nonumber
$$
называется единичной матрицей порядка (n) или просто единичной матрицей, если порядок известен.

Строки единичной матрицы отличаются от ее столбцов только формой записи.

Столбцы (строки) единичной матрицы линейно независимы и обладают тем свойством, что каждый столбец (строка) с тем же числом элементов раскладывается по ним.

Укажем несколько свойств линейно зависимых и линейно независимых систем матриц.

Система из (k > 1) матриц линейно зависима тогда и только тогда, когда хотя бы одна из матриц есть линейная комбинация остальных.

В самом деле, пусть система линейно зависима. По определению выполнено равенство вида eqref, где хотя бы один коэффициент отличен от нуля. Допустим для определенности, что это (alpha_). Тогда мы можем представить первую матрицу как линейную комбинацию
$$
A_=-frac<alpha_><alpha_>A_-ldots-frac<alpha_><alpha_>A_.
$$
Обратно, если одна из матриц разложена по остальным, то это разложение преобразуется к виду eqref, где один из коэффициентов равен 1.

Если некоторые из матриц (A_, ldots, A_) составляют сами по себе линейно зависимую систему, то вся система (A_, ldots, A_) линейно зависима.

Действительно, пусть существует нетривиальная линейная комбинация некоторых из матриц системы, равная нулевой матрице. Если мы добавим к ней остальные матрицы с нулевыми коэффициентами, то получится равная нулевой матрице нетривиальная линейная комбинация всех матриц.

В частности, если в систему матриц входит нулевая матрица, то система линейно зависима.

Любые матрицы, входящие в линейно независимую систему матриц, сами по себе линейно независимы.

В самом деле, в противном случае мы пришли бы к противоречию на основании предыдущего утверждения.

Если матрица (B) разложена по линейно независимой системе матриц (A_, ldots, A_), то коэффициенты разложения определены однозначно.

Действительно, пусть мы имеем два разложения
$$
B=alpha_A_+ldots+alpha_A_ mbox B=beta_A_+ldots+beta_A_.nonumber
$$
Вычитая одно разложение из другого, мы получаем
$$
O=(alpha_-beta_)A_+ldots+(alpha_-beta_)A_.nonumber
$$
Матрицы (A_, ldots, A_) линейно независимы, значит, (alpha_-beta_=0) для всех (i=1, ldots, k). Итак, коэффициенты обоих разложений совпадают.

Видео:Как разложить вектор по базису - bezbotvyСкачать

Линейная зависимость векторов. Базис системы векторов

Определение линейной зависимости системы векторов

Система векторов A₁, A₂. A_n называется линейно зависимой, если существует ненулевой набор чисел λ_1, λ₂. λ_n, при котором линейная комбинация векторов λ₁*A₁+λ₂*A₂+. +λ_n*A_n равна нулевому вектору, то есть система уравнений: A₁x₁+A₂x₂+. +A_nx_n =Θ имеет ненулевое решение.
Набор чисел λ_1, λ₂. λ_n является ненулевым, если хотя бы одно из чисел λ_1, λ₂. λ_n отлично от нуля.

Определение линейной независимости системы векторов

Система векторов A₁, A₂. A_n называется линейно независимой, если линейная комбинация этих векторов λ₁*A₁+λ₂*A₂+. +λ_n*A_n равна нулевому вектору только при нулевом наборе чисел λ_1, λ₂. λ_n, то есть система уравнений: A₁x₁+A₂x₂+. +A_nx_n =Θ имеет единственное нулевое решение.

Проверить, является ли линейно зависимой система векторов

Решение:

1. Составляем систему уравнений:

2. Решаем ее методом Гаусса. Преобразования Жордано системы приведены в таблице 1. При расчете правые части системы не записываются так как они равны нулю и при преобразованиях Жордана не изменяются.

3. Из последних трех строк таблицы записываем разрешенную систему, равносильную исходной системе:

4. Получаем общее решение системы:

5. Задав по своему усмотрению значение свободной переменной x₃ =1, получаем частное ненулевое решение X=(-3,2,1).

Ответ: Таким образом, при ненулевом наборе чисел (-3,2,1) линейная комбинация векторов равняется нулевому вектору -3A₁+2A₂+1A₃=Θ. Следовательно, система векторов линейно зависимая.

Свойства систем векторов

Свойство (1)
Если система векторов линейно зависимая, то хотя бы один из векторов разлагается по остальным и, наоборот, если хотя бы один из векторов системы разлагается по остальным, то система векторов линейно зависимая.

Свойство (2)
Если какая-либо подсистема векторов линейно зависимая, то и вся система линейно зависимая.

Свойство (3)
Если система векторов линейно независимая, то любая ее подсистема линейно независимая.

Свойство (4)
Любая система векторов, содержащая нулевой вектор, линейно зависимая.

Свойство (5)
Система m-мерных векторов всегда является линейно зависимой, если число векторов n больше их размерности (n>m)

Видео:Линейная алгебра, 6 урок, Ранг матрицыСкачать

Базис системы векторов

Базисом системы векторов A₁ , A₂ . A_n называется такая подсистема B₁, B₂ . B_r (каждый из векторов B₁,B₂. B_r является одним из векторов A₁ , A₂ . A_n)_, которая удовлетворяет следующим условиям:
1. B₁,B₂. B_r линейно независимая система векторов;
2. любой вектор A_j системы A₁ , A₂ . A_n линейно выражается через векторы B₁,B₂. B_r

r — число векторов входящих в базис.

Теорема «о единичном базисе системы векторов»

Если система m-мерных векторов содержит m различных единичных векторов E₁ E₂ . E_m , то они образуют базис системы.

Алгоритм нахождения базиса системы векторов

Для того, чтобы найти базис системы векторов A₁ ,A₂ . A_n необходимо:

• Составить соответствующую системе векторов однородную систему уравнений A₁x₁+A₂x₂+. +A_nx_n =Θ
• Привести эту систему

Видео:Линейная зависимость векторовСкачать

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 — x 1 ) · e ( 1 ) + ( x

2 — x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 — x 2 ) , . . . , ( x

n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 — 1 1 3 2 — 5 2 1 — 3

1 — 1 1 0 5 — 8 0 3 — 5

1 — 1 1 0 5 — 8 0 0 — 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x

1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x

1 ∆ = — 1 — 1 = 1 ∆ x

2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x

2 ∆ = — 1 — 1 = 1 ∆ x

3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Видео:Линейная зависимость и линейная независимость. ТемаСкачать

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

💥 Видео

Образуют ли данные векторы базисСкачать

Линейная зависимость и линейная независимость строк столбцов матрицы. Часть 1.Скачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

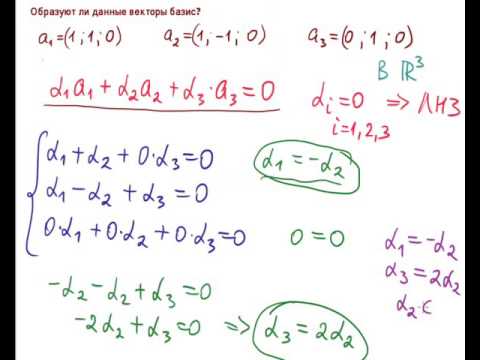
Линейная зависимость векторов на примерахСкачать

Линейная зависимость векторов. Линейная алгебра. Лекция 2Скачать

Система векторов: линейная зависимость и независимость, базис, ранг | 5 | Константин Правдин | ИТМОСкачать

Линейная зависимость и независимость систем векторовСкачать

Линейная оболочка. Базис и размерностьСкачать

Линейная комбинация. Линейная зависимость (независимость) матриц.Скачать

Линейная алгебра. Тема 6. Базис и ранг системы векторовСкачать