Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Высшая математика
Рассмотрим линейное однородное дифференциальное уравнение
Справедливо следующее этого уравнения.
Решения y 1( x ), y 2( x ), . y n( x ) линейного однородного дифференциального уравнения линейно независимы на отрезке [ a ; b ] тогда и только тогда, когда определитель Вронского этих функций W ( x ; y 1( x ), y 2( x ), . y n( x )) не обращается в нуль ни в одной точке отрезка [ a ; b ] .
Для определителя Вронского W ( x ; y 1( x ), y 2( x ), . y n( x )) решений y 1( x ), y 2( x ), . y n( x ) линейного однородного дифференциального уравнения с непрерывными на [ a ; b ] коэффициентами, справедлива формула Остроградского–Лиувилля:
Из формулы Остроградского-Лиувилля, в частности, следует:
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Лекция 20.
Линейная зависимость и независимость системы функций. Определитель Вронского, его свойства. Фундаментальная система решений однородного линейного дифференциального уравнения. Общее решение однородного уравнения.
Определение 20.1. Функции у1(х), у2(х),…, уп(х) называются линейно зависимыми на некотором отрезке [a,b], если существуют такие числа α1, α2,…, αп, хотя бы одно из которых не равно нулю, что
на рассматриваемом отрезке. Если же равенство (20.1) справедливо только при всех αi=0, функции у1(х), у2(х),…, уп(х) называются линейно независимымина отрезке [a,b].
- Функции 1, x, x², …, x n линейно независимы на любом отрезке, так как равенство α1 + α2x + α3x² + … + αn+1x n = 0 справедливо только при всех αi= 0. Иначе в левой части равенства стоял бы многочлен степени не выше п, который может обращаться в нуль не более, чем в п точках рассматриваемого отрезка.
- Линейно независимой на любом отрезке является система функций
. Если предположить, что эта система линейно зависима, то существуют такие числа α1, α2,…, αп(пусть для определенности
), что
. Разделим полученное равенство на
и продифференцируем:
. Проделав эту операцию п-1 раз, придем к равенству
, что невозможно, так как по предположению
.
- Подобным образом можно доказать линейную независимость системы функций
Определение 20.2. Определитель вида
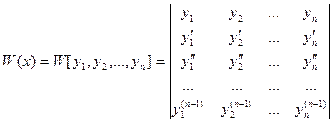
называется определителем Вронскогосистемы функций у1, у2,…, уп.
Теорема 20.1. Если функции у1, у2,…, уп линейно зависимы на отрезке [a,b], то их определитель Вронского на этом отрезке тождественно равен нулю.
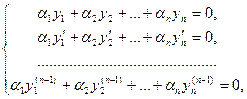
Теорема 20.2. Если линейно независимые функции у1, у2,…, уп являются решениями линейного однородного уравнения (19.2) с непрерывными на отрезке [a,b] коэффициентами, то определитель Вронского для этих функций не может обратиться в нуль ни в одной точке отрезка [a,b].
Пусть 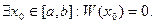
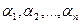
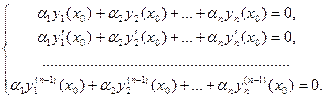
(Определитель этой системы, неизвестными в которой считаем 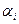
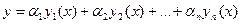
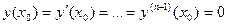
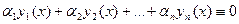
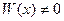
Замечание. В теореме 20.2 важно, что функции у1, у2,…, уп – решения уравнения (19.2). Для произвольной системы функций утверждение теоремы не справедливо.
Теорема 20.3. Общим решением на [a,b] уравнения (19.2) с непрерывными коэффициентами pi является линейная комбинация 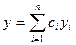
Доказательство. Для доказательства теоремы с учетом теоремы существования и единственности достаточно показать, что можно подобрать постоянные ci так, чтобы удовлетворялись произвольно заданные начальные условия:
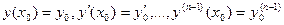
Подставив в равенства (20.6) выражение для у вида (20.5), получим линейную систему из п уравнений относительно неизвестных с1, с2,…, сп:
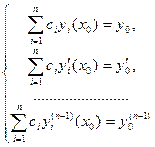
определителем которой является определитель Вронского для выбранных п линейно независимых решений рассматриваемого уравнения, который по теореме 20.2 не равен нулю. Следовательно, по правилу Крамера система имеет решение при любых правых частях. Теорема доказана.
Следствие. Максимальное число линейно независимых решений однородного уравнения (19.2) равно его порядку.
Определение 20.3. Любые п линейно независимых решений однородного линейного уравнения (19.2) называются его фундаментальной системой решений.
Таким образом, общее решение уравнения (19.2) является линейной комбинацией любой его фундаментальной системы решений.
Однородные линейные дифференциальные уравнения с постоянными коэффициентами. Построение фундаментальной системы решений. Неоднородные линейные дифференциальные уравнения. Частное и общее решения.
Определим вид частных решений однородного линейного уравнения
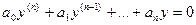
в котором коэффициенты ai постоянны. Можно показать, что они имеют вид 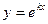
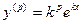
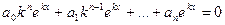
или, после сокращения на e kx ,
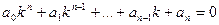
так называемое характеристическое уравнение для уравнения (21.1). Числа k, являющиеся его решениями, при подстановке в функцию 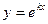
- Все корни уравнения (21.2) действительны и различны: k1, k2,…, kn . Тогда они задают максимально возможное количество линейно независимых решений уравнения (21.1) (их линейная независимость показана в примере 2 лекции 20), то есть определяют фундаментальную систему решений. Следовательно, в этом случае общее решение уравнения (21.1) может быть записано в виде:
. Пример. Общее решение уравнения
можно найти, решив характеристическое уравнение
. Разложим левую часть на множители:
. Следовательно, корни характеристического уравнения:
. Поэтому общее решение исходного уравнения имеет вид:
.
- Корни уравнения (21.2) различны, среди них есть комплексные. При этом, как было показано ранее, они образуют пары комплексно сопряженных чисел. При этом решения уравнения (21.1), соответствующие паре комплексно сопряженных решений уравнения (21.2)
и
, имеют вид
и
и могут быть заменены двумя действительными решениями: действительной и мнимой частями указанных решений. Следовательно, так как
, решениями уравнения (21.1) будут
и
. Пример.
- Характеристическое уравнение имеет кратные корни. В этом случае число линейно независимых решений предыдущих типов меньше п, и для получения фундаментальной системы нужно найти дополнительные решения иного вида. Докажем, что при наличии у характеристического уравнения корня ki кратности αiтакими решениями будут
Предположим вначале, что выбранный кратный корень ki = 0. Тогда характеристическое уравнение имеет вид:
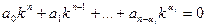
а соответствующее дифференциальное уравнение:
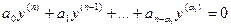
Очевидно, что частными решениями такого уравнения будут функции 1,x, x²,…, 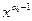
Пусть теперь корень характеристического уравнения ki кратности αi не равен нулю. Сделаем замену переменной: 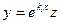
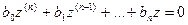
При этом корни характеристического уравнения
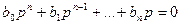
отличаются от корней уравнения
на слагаемое –ki, так как при 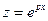
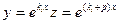
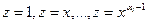
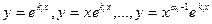
Таким образом, каждый кратный корень уравнения (21.2) задает серию линейно независимых частных решений уравнения (21.1), количество которых равно его кратности. Следовательно, вновь построена фундаментальная система решений.
Замечание. Кратные комплексно сопряженные корни задают частные решения вида 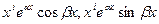
1. Характеристическое уравнение для уравнения 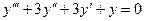
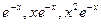
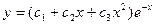
2. Для уравнения 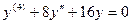
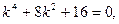
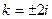
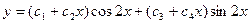
Видео:Видеоурок "Однородные системы линейных уравнений"Скачать

Определение общего решения СЛУ. Базисные и свободные неизвестные.
Системой уравнений называется общим решением совместная система A1x1+A2x2+…+Anxn=B (1), если выполняется следующее условие:
A1’x1+A2’x2+…+An’xn=B (2)
система (2) общее решение сист. (1)
условия:1)система (1) и (2) должны быть равносильны
2)система векторов A1,A2. An в сист. уравнений (2) явл. Разрешённой системой векторов
Набор неизвестных системы уравнения (1) называются базисными, если векторы при этих неизвестных образуют базис системы A1A2…An
не базисные неизвестные принято называть свободными.
Однородные СЛУ. Свойства однородной СЛУ. Теорема о нулевом и ненулевом решении СЛУ,
Однородная система — система, у которой все свободные члены равны нулю.
Однородная система—всегда совместна, так как x1=x2=x3=. =xn=0является решением системы.
Теоремы о ненулевых решениях однородной системы :
- Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т. е. r
а) вектора F1,F2..Fk линейно-независимы
б) k=n-r(A) – число решений равно разности количества неизвестных и ранга системы
Теорема об условии существования ФСР однородной СЛУ
Любое линейное однородное дифференциальное уравнение n -го порядка с непрерывными коэффициентами имеет фундаментальную систему решений, т.е. систему из n линейно независимых решений.
💥 Видео
Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Линейная зависимость векторов. РангСкачать

Линейная зависимость и линейная независимость векторов.Скачать

§41 Решение систем линейных однородных уравненийСкачать

Линейная зависимость и линейная независимость. ТемаСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Линейная зависимость векторовСкачать

Теорема о существовании фундаментальной системы решений системы линейных однородных уравнений.Скачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Решение однородных линейных систем. ТемаСкачать

Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Фундаментальная система решений для однородной системы линейных уравненийСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Линейно зависимые векторы: как доказать?Скачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Однородная система слау. Тривиальное решение. Ненулевое решениеСкачать



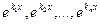 . Если предположить, что эта система линейно зависима, то существуют такие числа α1, α2,…, αп(пусть для определенности
. Если предположить, что эта система линейно зависима, то существуют такие числа α1, α2,…, αп(пусть для определенности 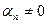 ), что
), что 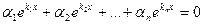 . Разделим полученное равенство на
. Разделим полученное равенство на 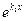 и продифференцируем:
и продифференцируем: 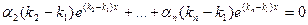 . Проделав эту операцию п-1 раз, придем к равенству
. Проделав эту операцию п-1 раз, придем к равенству 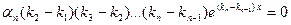 , что невозможно, так как по предположению
, что невозможно, так как по предположению 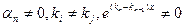 .
.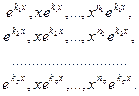
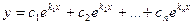 . Пример. Общее решение уравнения
. Пример. Общее решение уравнения 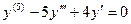 можно найти, решив характеристическое уравнение
можно найти, решив характеристическое уравнение 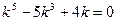 . Разложим левую часть на множители:
. Разложим левую часть на множители: 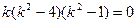 . Следовательно, корни характеристического уравнения:
. Следовательно, корни характеристического уравнения: 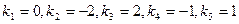 . Поэтому общее решение исходного уравнения имеет вид:
. Поэтому общее решение исходного уравнения имеет вид: 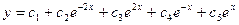 .
.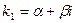 и
и 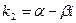 , имеют вид
, имеют вид 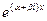 и
и 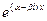 и могут быть заменены двумя действительными решениями: действительной и мнимой частями указанных решений. Следовательно, так как
и могут быть заменены двумя действительными решениями: действительной и мнимой частями указанных решений. Следовательно, так как 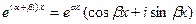 , решениями уравнения (21.1) будут
, решениями уравнения (21.1) будут 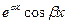 и
и 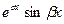 . Пример.
. Пример. 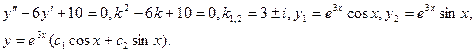

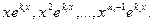 Предположим вначале, что выбранный кратный корень ki = 0. Тогда характеристическое уравнение имеет вид:
Предположим вначале, что выбранный кратный корень ki = 0. Тогда характеристическое уравнение имеет вид: