Линеаризующие преобразования для некоторых нелинейных уравнений регрессии (2 видео)

Тема 11. Нелинейные регрессии и их линеаризация

Аннотация.Данная тема раскрывает особенности построения нелинейных моделей регрессии.

Ключевые слова.Нелинейная регрессия, индекс корреляции, коэффициент эластичности, подход Бокса-Кокса.

Методические рекомендации по изучению темы

· Тема содержит лекционную часть, где даются общие представления по теме.

· В качестве самостоятельной работы предлагается ознакомиться с решениями типовых задач, выполнить практические задания и ответить на вопросы для самоконтроля.

· Для проверки усвоения темы имеется тест для самоконтроля.

· Для подготовки к экзамену имеется контрольный тест.

Рекомендуемые информационные ресурсы:

2. Эконометрика: [Электронный ресурс] Учеб. пособие / А.И. Новиков. — 3-e изд., испр. и доп. — М.: ИНФРА-М, 2014. — 272 с.: (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=1#none) С. 41-45.

3.Уткин, В. Б. Эконометрика [Электронный ресурс] : Учебник / В. Б. Уткин; Под ред. проф. В. Б. Уткина. — 2-е изд. — М.: Издательско-торговая корпорация «Дашков и К°», 2012. — 564 с.

(http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С. 383-399.

4. Эконометрика. Практикум: [Электронный ресурс] Учебное пособие / С.А. Бородич. — М.: НИЦ ИНФРА-М; Мн.: Нов. знание, 2014. — 329 с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С.172-174.

Глоссарий

Бокса-Кокса подход – способ подбора линеаризующего преобразования.

Индекс корреляции—показатель корреляции, который определяется для нелинейных регрессий.

Коэффициент эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 процент.

Линеаризация нелинейных моделей – процедура, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований.

Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду.

Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции.

Вопросы для изучения

1. Классы и виды нелинейных регрессий.

2. Линеаризация нелинейных моделей. Выбор формы модели.

3. Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса).

Классы и виды нелинейных регрессий. Различают два класса нелинейных регрессий: регрессии, нелинейные относительно включенных в анализ объясняющих переменных; регрессии, нелинейные по оцениваемым параметрам. Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду. Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции. При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации.

Линеаризация нелинейных моделей. Выбор формы модели. В нелинейных зависимостях, не являющихся классическими полиномами, обязательно проводится предварительная линеаризация, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований. Рассмотрим некоторые классы таких зависимостей.

Рис. 11.1. Способы линеаризации

Замена переменных заключается в замене нелинейных объясняющих переменных новыми линейными переменными и сведении нелинейной регрессии к линейной. Логарифмирование обеих частей уравнения применяется обычно, когда мультипликативную модель необходимо привести к линейному виду. К классу степенных функций относятся: кривые спроса и предложения, производственная функция Кобба-Дугласа, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения и выпуска нового вида изделий, зависимость валового национального дохода от уровня занятости.

Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса). Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:

Здесь — общая дисперсия результативного признака y, — остаточная дисперсия, определяемая по уравнению нелинейной регрессии . По-другому можно записать так:

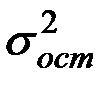
Следует обратить внимание на то, что разности в соответствующих суммах и берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. Величина R находится в границах , и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

Если разные модели используют разные функциональные формы для зависимой переменной, то проблема выбора модели становится более сложной, так как нельзя непосредственно сравнивать коэффициенты R 2 или суммы квадратов отклонений. Например, нельзя сравнивать эти статистики для линейного и логарифмического вариантов. Пусть в линейной модели в качестве зависимой переменной используется заработок, а в нелинейной – логарифм заработка. Тогда R 2 в одном уравнении измеряет объясненную регрессией долю дисперсии заработка, а в другом — объясненную регрессией долю дисперсии логарифма заработка. В случае, если значения R 2 для двух моделей близки друг к другу, проблема выбора усложняется. Здесь следует использовать тест Бокса – Кокса. При сравнении моделей с использованием в качестве зависимой переменной y и lny проводится такое преобразование масштаба наблюдений y, при котором можно непосредственно сравнивать суммы квадратов отклонений в линейной и логарифмической моделях. Здесь выполняются следующие шаги. Вычисляется среднее геометрическое значений y в выборке. Оно совпадает с экспонентой среднего арифметического логарифмов y. Все значения y пересчитываются делением на среднее геометрическое, получаем значения y*. Оцениваются две регрессии: для линейной модели с использованием y* в качестве зависимой переменной и для логарифмической модели с использованием ln y* вместо ln y. Во всех других отношениях модели должны оставаться неизменными. Теперь значения СКО для двух регрессий сравнимы, и модель с меньшей остаточной СКО обеспечивает лучшее соответствие исходным данным. Для проверки, обеспечивает ли одна из моделей значимо лучшее соответствие, можно вычислить величину (n/2)lnz, где z – отношение значений остаточной СКО в перечисленных регрессиях. Эта статистика имеет распределение хи – квадрат с одной степенью свободы. Если она превышает критическое значение при выбранном уровне значимости α, то делается вывод о наличии значимой разницы в качестве оценивания.

Величина коэффициента эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 %:

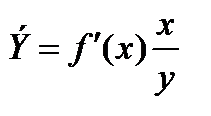
В заключение приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии:

Вид уравнения регрессии	Коэффициент эластичности

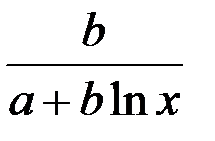Вопросы и задания для самоконтроля

1. Какие модели являются нелинейными относительно: а) включаемых переменных; б) оцениваемых параметров?

2. Какие преобразования используются для линеаризации нелинейных моделей?

3. Чем отличается применение МНК к моделям, нелинейным относительно включаемых переменных, от применения к моделям, нелинейным по оцениваемым параметрам?

4. Как определяются коэффициенты эластичности по разным видам регрессионных моделей?

5. Какие показатели корреляции используются при нелинейных соотношениях рассматриваемых признаков?

6. В каких случаях используют обратные и степенные модели?

Задача 1.По группе предприятий, производящих однородную продукцию известно, как зависит себестоимость единицы продукции (Y) от факторов, приведенных в таблице:

Признак-фактор	Уравнение парной регрессии	Среднее значение фактора
Объем производства, млн. руб.
Трудоемкость единицы продукции, чел/час
Оптовая цена за 1т энергоносителя, , млн. руб.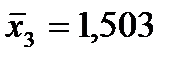
Доля прибыли, изымаемая государством, ,%

1) определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат;

2) ранжировать факторы по силе влияния на результат.

Задача 2. По группе из 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции (тыс. руб) от уровня технической оснащенности (тыс. руб.)

Доля остаточной дисперсии в общей составила 0,19.

1) определить коэффициент эластичности, предполагая, что стоимость активных производственных фондов составляет 200 тыс. руб.;

2) вычислить индекс корреляции;

3) оценить значимость уравнения регрессии с помощью критерия.

Содержание

Линеаризация нелинейных моделей регрессии
Понятие регрессии
Нелинейные модели регрессии
Готовые работы на аналогичную тему
Линеаризация нелинейных моделей регрессии
Нелинейные модели, поддающиеся линеаризации. Подход Бокса-Кокса подбора линеаризующего преобразования
курсовая2.doc
📹 Видео

Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Линеаризация нелинейных моделей регрессии

Вы будете перенаправлены на Автор24

Видео:Эконометрика. Нелинейная регрессия. Степенная функция.Скачать

Понятие регрессии

Регрессия – это односторонняя зависимость, которая устанавливает соответствие между случайными величинам.

Сущность регрессии заключается в том, чтобы через математическое выражение установить связь между зависимой и независимыми переменными. Ее отличительной особенностью от функциональной зависимости является тот факт, что каждому значению независимой соответствует одно определенное значение зависимой. В регрессионной связи одной и той же величине могут соответствовать абсолютно разные величины.

Впервые регрессию стали использовать в конце девятнадцатого века. Она была применена для установления зависимости между параметрами человека. Регрессию смогли перенести на плоскость. Точки легли на одну прямую, поэтому ее назвали линейной.

Построение линейной регрессии подразумевает, что ошибок в ней нет. Тогда распределение величин происходит под влиянием нормального закона. То есть, среднее значение равно нулю, а отклонение постоянно.

Чтобы вычислить параметры модели часто применяют программное обеспечение. Оно позволяет обрабатывать большие массивы информации с минимальными ошибками. Существуют специальные методы, позволяющие проверить величину отклонения. Ошибки необходимы для того, чтобы находить доверительные интервалы и проверять выдвинутые в начале исследования гипотезы. Например, в статистике используется критерий Стьюдента, позволяющий сопоставить средние значения двух выборок.

Самое простое представление регрессии состоит из зависимости между соотношениями случайной и независимой величины. Этот подход необходим для установления функциональной связи, если величины не случайны. В практической деятельности коэффициенты неизвестны, поэтому их исследуют с помощью экспериментальных данных.

Видео:Парная нелинейная регрессияСкачать

Нелинейные модели регрессии

Построение нелинейной регрессии осуществляется для того, чтобы провести анализ. В нем экспериментальные данные записываются в функциональную зависимость, описывающей нелинейную комбинацию, представляющую модель, которая зависит от одной или нескольких переменных. Чтобы приблизить полученные данные к практическим величинам используется метод последовательных приближений.

Готовые работы на аналогичную тему

Этот метод заключается в следующем. Исследователем определяются корни уравнения или системы уравнений для того, чтобы упростить решаемую задачу, либо определить неизвестные параметры.

Структура нелинейной регрессии состоит из независимых и зависимых переменных. Для каждой переменной устанавливается случайная величина со средним значением. Погрешность может появиться, но есть ее обрабатывать, то она выйдет за пределы модели. В случае, если переменные не свободны, то модель становится ошибочной, поэтому для исследования становится непригодной.

Вот некоторые примеры нелинейных функций:

Показательные.
Логарифмические.
Тригонометрические.
Степенные.
Функция Гаусса.
Кривые Лоуренца.

В некоторых случаях регрессионный анализ может быть сведен к линейному, но данный способ должен применяться с осторожностью. Чтобы получить наилучший вариант расчета применяются оптимизационные алгоритмы. На практике могут применяться оценочные значения совместно с методиками оптимизации. В результате надо найти глобальный минимум суммы квадратов.

Нелинейная регрессия чаще всего применяется, как статистика линейной. Это позволяет сместить статистику, поэтому полученные данные интерпретируются с осторожностью.

Видео:Парная регрессия: линейная зависимостьСкачать

Линеаризация нелинейных моделей регрессии

Линеаризация – это преобразование. Оно осуществляется для того, чтобы упростить определенные модели и вычисления. Например, применение логарифма к обеим частям линейной регрессии позволяет оценить неизвестные параметры более простым способом.

Но использование нелинейного изменения уравнения требует осторожности. Это связано с тем, что данные будут изменяться. Поэтому появятся ошибки модели. Их интерпретация может привести к ошибочному суждению о гипотезе. Обычно в нелинейных уравнениях используется модель Гаусса для исследования ошибок, что необходимо учитывать при проверке.

В которых случаях применяется уравнение Лайнуивер – Берк, либо обобщенная линейная модель.

Чтобы уточнить построенную модель и снизить вероятность ошибок, независимая переменная разбивается на классы. Вследствие этого линейная регрессия разбивается посегментно. Она может дать результат, в котором будет видно, как ведет себя параметр в зависимом положении. Отображение изменений производится графически.

То есть сущность линеаризации заключается в том, что исследователь применяет особые методики для того, чтобы провести преобразования исходных данных. Это позволяет исследовать нелинейную зависимость. Переменные нелинейного уравнения преобразуются с помощью специальных методик в линейные. Это может привести к ошибкам, что необходимо учитывать в процессе преобразования уравнения. Метод может быть опасным, так как влияет на результат вычислений.

Сущность метода заключается в том, что нелинейные переменные заменяются линейными. Регрессия сводится к линейной. Такой подход часто используется для полиномов. Далее применяются известные и простые оценки исследования линейных регрессии. Но изменение полиномов должно так же проводиться с осторожностью. Чем выше порядок полинома, тем сложнее удержаться в рамках реалистичной интерпретации коэффициентов регрессии.

В логарифмических моделях составляется линейная модель с новыми переменными. Оценка результата происходит с помощью метода наименьших квадратов. Эта методика подходит для исследования кривых спроса и предложения, производственных функций, кривых освоения связи между трудоемкостью и производственными масштабами. Такой подход актуален при запуске новых видов продукции.

Видео:Нелинейная регрессияСкачать

Нелинейные модели, поддающиеся линеаризации. Подход Бокса-Кокса подбора линеаризующего преобразования

Автор: Пользователь скрыл имя, 05 Марта 2013 в 15:17, курсовая работа

Краткое описание

Основными задачами эконометрики являются: получение наилучших оценок параметров экономико-математических моделей, конструируемых в прикладных целях; проверка теоретико-экономических положений и выводов на фактическом (эмпирическом) материале; создание универсальных и специальных методов для обнаружения статистических закономерностей в экономике.

Файлы: 1 файл

Видео:Как работает метод наименьших квадратов? Душкин объяснитСкачать

курсовая2.doc

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

« Кубанский Государственный Университет»

Филиал в г. Кореновске

Специальность прикладная информатика (в экономике)

«Нелинейные модели, поддающиеся линеаризации.
Подход Бокса-Кокса подбора линеаризующего преобразования»

Работу выполнила: Волощук К.В.

Специальность 08081 Прикладная информатика (в экономике)

Научный руководитель: к.ф. – м.н. Калайдина Г. В.

г. Кореновск. 2010.г

I.I. Нелинейная регрессия 2

I.II. Линеаризация 9

II. Метод Бокса-Кокса 13

Список литературы 16

На стыке экономической практики и математической статистики в начале 30-х годов зародилась новая самостоятельная дисциплина, получившая название «Эконометрика».

Эконометрика — это наука, которая изучает статистические закономерности в экономике.

Объектом изучения эконометрики, как самостоятельного раздела математической экономики, являются экономико-математические модели, которые строятся с учетом случайных факторов. Такие модели называются эконометрическими моделями. Исследование эконометрических моделей проводится на основе статистических данных об изучаемом объекте и с помощью методов математической статистики.

I.I. Нелинейная регрессия

Линейная регрессия и методы ее исследования и оценки не имели бы столь важного значения, если бы помимо этого весьма важного, но все же простейшего случая мы не получали бы с их помощью инструмента анализа более сложных нелинейных зависимостей. Нелинейные регрессии могут быть разделены на два существенно различных класса. Первым и более простым является класс нелинейных зависимостей, в которых имеется нелинейность относительно объясняющих переменных, но которые остаются линейными по входящим в них и подлежащим оценке параметрам. Сюда входят полиномы различных степеней и равносторонняя гипербола.

Такая нелинейная регрессия по включенным в объяснение переменным простым их преобразованием (заменой) легко сводится к обычной линейной регрессии для новых переменных. Поэтому оценка параметров в этом случае выполняется просто по МНК, поскольку зависимости линейны по параметрам. Так, важную роль в экономике играет нелинейная зависимость, описываемая равносторонней гиперболой:

Ее параметры хорошо оцениваются по МНК и сама такая зависимость характеризует связь удельных расходов сырья, топлива, материалов с объемом выпускаемой продукции, временем обращением товаров и всех этих факторов с величиной товарооборота. Например, кривая Филлипса характеризует нелинейное соотношение между нормой безработицы и процентом прироста заработной платы.

Совершенно по-другому обстоит дело с регрессией, нелинейной по оцениваемым параметрам, например, представляемой степенной функцией, в которой сама степень (ее показатель) является параметром или зависит от него. Также это может быть показательная функция, где основанием степени является параметр и экспоненциальная функция, в которой опять же показатель содержит параметр или комбинацию параметров. Этот класс, в свою очередь, делится на два подкласса: к одному относятся внешне нелинейные, но по существу внутренне линейные. В этом случае можно привести модель к линейному виду с помощью преобразований. Однако, если модель внутренне нелинейна, то она не может быть сведена к линейной функции.

Таким образом, только модели внутренне нелинейные в регрессионном анализе считаются действительно нелинейными. Все прочие, сводящиеся к линейным посредством преобразований, таковыми не считаются, и именно они рассматриваются чаще всего в эконометрических исследованиях. В то же время это не означает невозможности исследования в эконометрике существенно нелинейных зависимостей. Если модель внутренне нелинейна по параметрам, то для оценки параметров используются численные итеративные процедуры, успешность которых зависит от вида уравнения и от особенностей применяемого итеративного метода.

Вернемся к зависимостям, приводимым к линейным. Если они нелинейны и по параметрам и по переменным, например, вида у = а, умноженному на степень х, показатель которой и есть параметр β (бета):

Очевидно, такое соотношение легко преобразуется в линейное уравнение простым логарифмированием:

После введения новых переменных, обозначающих логарифмы, получается линейное уравнение. Тогда процедура оценивания регрессии состоит в вычислении новых переменных для каждого наблюдения путем взятия логарифмов от исходных значений. Затем оценивается регрессионная зависимость новых переменных. Для перехода к исходным переменным следует взять антилогарифм, т.е. фактически вернуться к самим степеням вместо их показателей (ведь логарифм это и есть показатель степени). Аналогично может рассматриваться случай показательных, или экспоненциальных, функций.

Для существенно нелинейной регрессии невозможно применение обычной процедуры оценивания регрессии, поскольку соответствующая зависимость не может быть преобразована в линейную. Общая схема действий при этом следующая.

Принимаются некоторые правдоподобные исходные значения параметров.
Вычисляются предсказанные значения у по фактическим значениям х с использованием этих значений параметров.
Вычисляются остатки для всех наблюдений в выборке и затем сумма квадратов остатков.
Вносятся небольшие изменения в одну или более оценку параметров.
Вычисляются новые предсказанные значения у, остатки и сумма квадратов остатков.
Если сумма квадратов остатков меньше, чем прежде, то новые оценки параметров лучше прежних и их следует использовать в качестве новой отправной точки.
Шаги 4, 5 и 6 повторяются вновь до тех пор, пока не окажется невозможным внести такие изменения в оценки параметров, которые привели бы к изменению суммы остатков квадратов.
Делается вывод о том, что величина суммы квадратов остатков минимизирована и конечные оценки параметров являются оценками по методу наименьших квадратов.

Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрике широко используется степенная функция. Параметр b в ней имеет четкое истолкование, являясь коэффициентом эластичности. В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Практическое применение логарифмирования и, соответственно, экспоненты возможно тогда, когда результативный признак не имеет отрицательных значений. При исследовании взаимосвязей среди функций, использующих логарифм результативного признака, в эконометрике преобладают степенные зависимости (кривые спроса и предложения, производственные функции, кривые освоения для характеристики связи между трудоемкостью продукции, масштабами производства, зависимость ВНД от уровня занятости, кривые Энгеля).

Иногда используется так называемая обратная модель, являющаяся внутренне нелинейной, но в ней, в отличие от равносторонней гиперболы, преобразованию подвергается не объясняющая переменная, а результативный признак у. Поэтому обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений результативного признака у, а для их обратных значений.

Особого внимания заслуживает исследование корреляции для нелинейной регрессии. В общем случае парабола второй степени, так же как и полиномы более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции.

Если преобразования уравнения регрессии в линейную форму связаны с зависимой переменной (результативным признаком), то линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку связи и численно не совпадает с индексом корреляции. Следует иметь в виду, что при расчете индекса корреляции используются суммы квадратов отклонений результативного признака у, а не их логарифмов. Оценка значимости индекса корреляции выполняется так же, как оценка надежности (значимости) коэффициента корреляции. Сам индекс корреляции, как и индекс детерминации, используется для проверки значимости в целом уравнения нелинейной регрессии по F-критерию Фишера.

Отметим, что возможность построения нелинейных моделей как посредством приведения их к линейному виду, так и путем использования нелинейной регрессии, с одной стороны, повышает универсальность регрессионного анализа, а с другой — существенно усложняет задачи исследователя. Если ограничиваться парным регрессионным анализом, то можно построить график наблюдений у и х как диаграмму разброса. Часто несколько различных нелинейных функций приблизительно соответствуют наблюдениям, если они лежат на некоторой кривой. Но в случае множественного регрессионного анализа такой график построить невозможно.

При рассмотрении альтернативных моделей с одним и тем же определением зависимой переменной выбор прост. Разумнее всего оценивать регрессию на основе всех вероятных функций, останавливаясь на функции, в наибольшей степени объясняющей изменения зависимой переменной. Если коэффициент детерминации измеряет в одном случае объясненную регрессией долю дисперсии, а в другом — объясненную регрессией долю дисперсии логарифма этой зависимой переменной, то выбор делается без затруднений. Другое дело, когда эти значения для двух моделей весьма близки и проблема выбора существенно осложняется.

Тогда следует применять стандартную процедуру в виде теста Бокса — Кокса. Если нужно всего лишь сравнить модели с использованием результативного фактора и его логарифма в виде варианта зависимой переменой, то применяют вариант теста Зарембки. В нем предлагается преобразование масштаба наблюдений у, при котором обеспечивается возможность непосредственного сравнения среднеквадратичной ошибки (СКО) в линейной и логарифмической моделях. Соответствующая процедура включает следующие шаги.

Вычисляется среднее геометрическое значений у в выборке, совпадающее с экспонентой среднего арифметического значений логарифма от у.
Пересчитываются наблюдения у таким образом, что они делятся на полученное на первом шаге значение.
Оценивается регрессия для линейной модели с использованием пересчитанных значений у вместо исходных значений у и для логарифмической модели с использованием логарифма от пересчитанных значений у. Теперь значения СКО для двух регрессий сравнимы, и поэтому модель с меньшей суммой квадратов отклонений обеспечивает лучшее соответствие с истинной зависимостью наблюденных значений.
Для проверки того, что одна из моделей не обеспечивает значимо лучшее соответствие, можно использовать произведение 1/2 числа наблюдений на логарифм отношения значений СКО в пересчитанных регрессиях с последующим взятием абсолютного значения этой величины. Такая статистика имеет распределение χ 2 с одной степенью свободы (обобщение нормального распределения).

Для оценки параметров нелинейных моделей используются два подхода. Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.

Второй подход обычно применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных.

Для линеаризации модели в рамках первого подхода могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам.

Если модель нелинейна по переменным, то введением новых переменных ее можно свести к линейной модели, для оценки параметров которой использовать обычный метод наименьших квадратов.

Так, например, если нам необходимо оценить параметры регрессионной модели