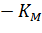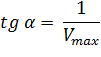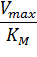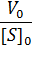Константу Михаэлиса можно определить из графика Михаэлиса (рис.2.2.1), найдя графическим способом максимальную скорость и соответствующую величину концентрации субстрата, при которой скорость ферментативной реакции будет вдвое меньше Vmax. Эта величина [S] и будет Км. Таким способом можно определить только приблизительную величину константы Михаэлиса из-за трудности точного графического определения Vmax.
Более удобными являются методы, в которых осуществлена линеаризация уравнения Михаэлиса-Ментен, т. е. гиперболическая зависимость v от [S] переведена в линейную.
Для того чтобы построить такой график, необходимо определить в одинаковых условиях при различных концентрациях субстрата и [E]= const начальные скорости ферментативной реакции.
Метод Лайнуивера-Берка. Один из способов линеаризации уравнения Михаэлиса-Ментен предложили Лайнуивер и Берк (Lineweaver H., Burk D.). Это так называемый метод двойных обратных величин. Для линеаризации необходимо взять обратные величины от левой и правой частей уравнения (3), в результате чего оно преобразуется в уравнение вида,
согласно которому между величинами, обратными начальной скорости (1/v, v -1 ) и концентрации субстрата (1/[S], [S] -1 ) соблюдается линейная зависимость, если механизм реакции подчиняется изложенным выше представлениям (рис.2.2.3).
Рис. 2.2.3. График зависимости 1/v от 1/[S] (график Лайнуивера-Берка)
Экспериментальная прямая пересекает ось абсцисс в точке (-1/[S] = 1/Км), а ось ординат – в точке (1/v = 1/Vмах). Тангенс угла наклона равен Км/Vмах. Этим широко пользуются для определения параметров Км и Vмах, характеризующих связывающую и каталитическую функции ферментов.
Метод Хайнса-Вульфа. В этом случае преобразуется уравнение Лайнуивера-Берка путем умножения правой и левой частей на концентрацию субстрата.
Графическая зависимость приведена на рис.2.2.4.
Рис. 2.2.4. График зависимости [S]/v от [S] (график Хайнса-Вульфа)
Это прямая с наклоном 1/Vmax, отсекающая на осях [S]/v и [S] отрезки Км/ Vmax и – Км соответственно.
Метод Иди-Хофсти. При одном из таких графических преобразований в так называемом графике Иди-Хофсти(pиc.2.2.5) строят график зависимости v от v/[S]. В этом случае точка пересечения прямой, полученной путем наилучшей линейной аппроксимации экспериментальных точек, с осью ординат соответствует Vmax, а тангенс угла наклона равен – Km. Данный способ линеаризации приведен на рис. 2.2.5.
Рис. 2.2.5. График зависимости v от v/[S] (график Эди-Хофсти)
Метод Эйзенталя и Корниш-Боудена. Много позднее Эйзенталь и Корниш-Боуден предложили иной метод графического представления результатов исследования кинетики ферментативных реакций – так называемый прямой линейный график. Уравнение Михаэлиса-Ментен они преобразовали в виде зависимости Vmax от Км:
Для любой пары значений [S] и v можно построить зависимость Vmax от Км. Она представляет прямую с наклоном, равным v/[S], и отрезками, отсекаемыми на осях Км и Vmax, соответственно равными -[S] v. Если провести прямые для нескольких пар значений [S] и v, то эти прямые пересекутся в одной точке, координаты которой дадут единственные значения Vmax от Км, удовлетворяющие всем парам значений [S] и v (рис.2.2.6).
Преимущества такого графика очевидно: для его построения не требуется никаких расчетов, он позволяет очень просто выявить ошибочные данные (иакие прямые будут выпадать из основной совокупности прямых).
Уравнение Михаэлиса лежит в основе всех кинетических исследований ферментативных реакций, так как оно позволяет рассчитать количественные характеристики ферментов и проводить анализ их ингибирования. Величины Кm и Vmax являются важнейшими характеристиками ферментов и их можно определить, используя линеаризованные формы уравнения Михаэлиса-Ментен.
В заключении необходимо отметить, что графические методы для определения V и Кm не являются оптимальными. В настоящее время данные ферментативной кинетики обрабатывают быстрее и более объективно с помощью компьютерных программ.
Процессы, приводящие к денатурации фермента, могут иметь различную физико-химическую природу. Конформация белковой молекулы в растворе зависит от двух показателей – величины рН и температуры. Повышение температуры приводит к нарушению системы слабых связей, стабилизирующих белковую молекулу. Длительное воздействие повышенной температуры приводит к необратимым изменениям структуры фермента, сопровождающимся потерей активности (тепловая денатурация).
Каждый фермент характеризуется соответствующим зарядом, создаваемым ионогенными группами аминокислотных остатков. При очень низких или высоких значениях рН изменение степени ионизации функциональных групп может приводить к необратимым нарушениям нативной конформации молекулы фермента с разрушением структуры активного центра.
Конформационные изменения в белковой молекулу сопровождаются изменениями спектров поглощения и флуоресценции ароматических аминокислот – тирозина и триптофана в ультрафиолетовой области спектра (
290 нм), что позволяет отслеживать изменения в структуре фермента. Обратимые конформационные, вызванные изменением температуры или концентрацией протонов водорода, осуществляются в течение 10 -4 – 10 -1 с, необратимые денатурационные изменения в зависимости от условий – в течение 1-10 3 мин. Более подробный анализ кинетики денатурации ферментов рассмотрен в Теме 5 учебного пособия по самостоятельной работе.
Видео:Биохимия | Кинетика ферментативных реакций: константа Михаэлиса и график Лайнуивера-БеркаСкачать

Лекция_методы определения константы михаэлиса и максимальной скорости процесса
Существует несколько методов определения параметров уравнения Михаэлиса-Ментен (константы Михаэлиса и максимальной скорости реакции) для односубстратной реакции. Наиболее распространенный из них – линеаризация уравнения Михаэлиса-Ментен. Полный анализ включает определение не только Vmax и KM, но и KS, k1, k-1, k2.
Из кривой, построенной на основе исходного уравнения Михаэлиса-Ментен, можно определить графическим методом значения констант Vmax и KM, но это неудобно, так как невозможно провести асимптоту к гиперболе с хорошей точностью.
Первый способ линеаризации был описан Холдейном и Штерном в их учебнике по энзимологии. Для осуществления такого преобразования уравнение Михаэлиса-Ментен представляют в двойных обратных координатах, то есть, единицу делят на V0 и переворачивают дробь в правой части уравнения:
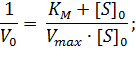 | (1) |
Преобразовав уравнение (1), получаем один из часто применяемых способов линеаризации – уравнение Лайнуивера-Берка:
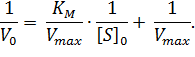 | (2) |
При построении зависимости в двойных обратных координатах, 1/V0 от 1/[S]0, как показано на рисунке 1, получаем прямую. Из уравнения линейной регрессии можно определить интересующие константы.
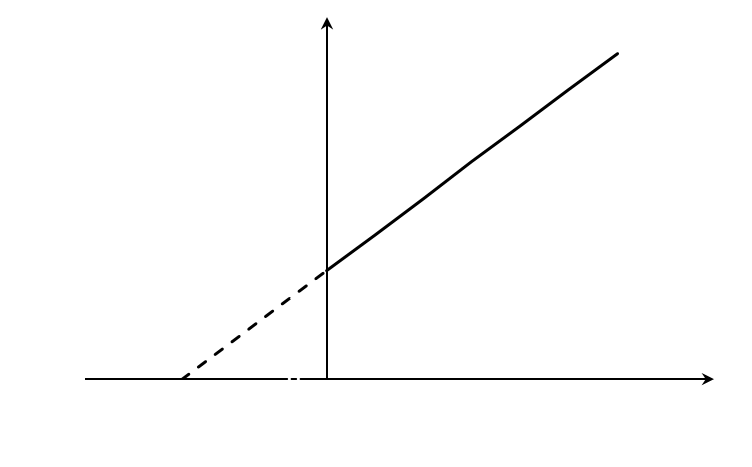 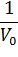 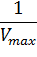 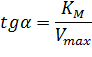 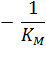 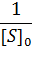 |
| Рисунок 1 – Зависимость начальной скорости реакции от начальной концентрации субстрата в координатах уравнения Лайнуивера-Берка. |
Отсекаемый отрезок на оси ординат дает обратную максимальную скорость, а на оси абсцисс – обратную константу Михаэлиса с противоположным знаком. Или же определяют непосредственно из уравнения прямой обратную максимальную скорость, а потом константу Михаэлиса из тангенса угла наклона прямой (рисунок 1).
Точность определения кинетических параметров таким способом считается невысокой. Чем меньше концентрация субстрата, тем выше оказывается ошибка определения обратной скорости.
Домножив обе части уравнения (2) на начальную концентрацию субстрата [S]0, получаем уравнение Хейнса:
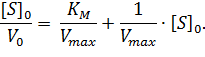 | (3) |
Построив зависимость [S]0/V0 от [S]0, как показано на рисунке 2, получим прямую, из уравнения линейной регрессии которой можно определить параметры Vmax и KM.
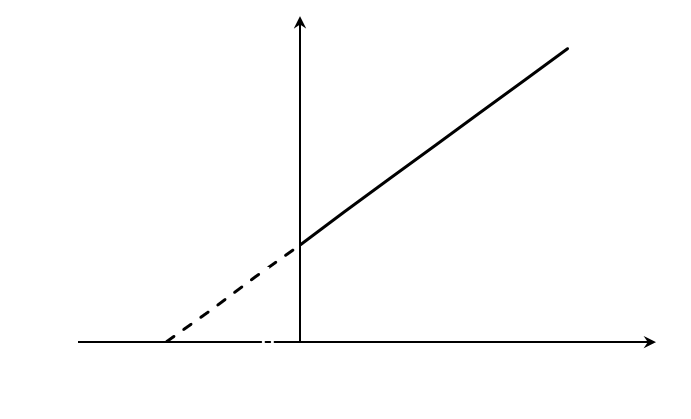
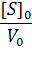
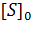
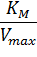
Существует еще один вариант преобразования уравнения Михаэлиса-Ментен. Для его осуществления избавляются от знаменателя, умножив на него обе части исходного уравнения и делят обе части на 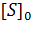
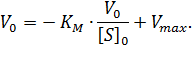 | (4) |
Мы получили уравнение Иди-Хофсти. Его графиком является прямая в координатах V0 от [S]0/V0, из уравнения линейной регрессии которой можно определить те же кинетические параметры — Vmax и KM в соответствии с рисунком 3.
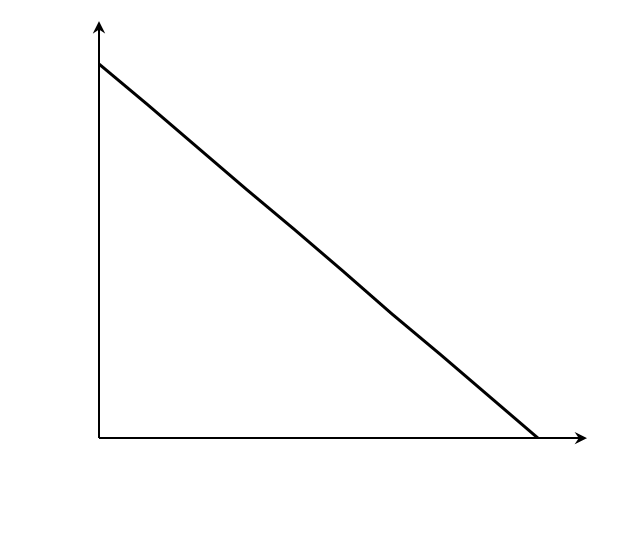
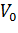
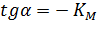
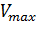
Статистический анализ показывает, что методы Хейнса и Иди-Хофсти дают более точные результаты, чем метод Лайнуивера-Берка. Причиной этого является то, что в первых двух графиках и зависимые, и независимые переменные входят в величины, откладываемые на обеих осях координат.
Нередко наблюдается спрямление экспериментальных данных в координатах уравнения Лайнуивера-Берка и невозможность такого преобразования по остальным уравнениям. Это говорит о том, что результаты, полученные посредством одной линеаризации, не слишком надежды и необходимо применять все три одновременно.
Очень точный графический метод – «прямой график» Эйзенталя-Боудена. Каждой начальной концентрации субстрата [S]i соответствует значение начальной скорости Vi (i = 1,2,…n). Значения [S]i с обратным знаком откладываются на оси абсцисс, на оси ординат – значения Vi. Через полученные пары точек проводят прямые, пересекающие координатные оси в точках (-[S]i, 0) и (0, Vi). Проекция общей точки пересечения прямых на горизонтальную ось равна КМ, а на вертикальную – Vmax (рисунок 4).
Разброс экспериментальных данных в этом методе учитывают с помощью нахождения медианы (в случае непрерывных распределений медианой является место, выше и ниже которого находится по 50% экспериментальных значений; другими словами, значения, лежащие ниже и выше медианы, встречаются с вероятностью 0,5).
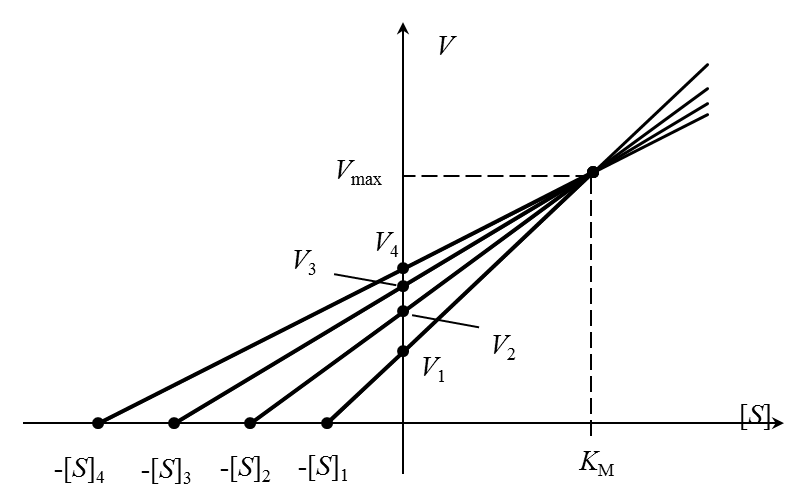 |
| Рисунок 4 – Определение констант уравнения Михаэлиса-Ментен по методу Корниш-Боудена. |
Для определения максимальной скорости и константы Михаэлиса применяют также метод Диксона, согласно которому точку начала координат соединяют прямыми линиями с точками на кривой уравнения Михаэлиса-Ментен, соответствующими значениям 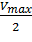
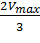
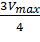
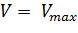
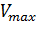
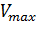
— если рассчитанная 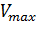
— если рассчитанная 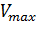
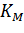
То есть, метод позволяет установить точность определения 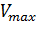
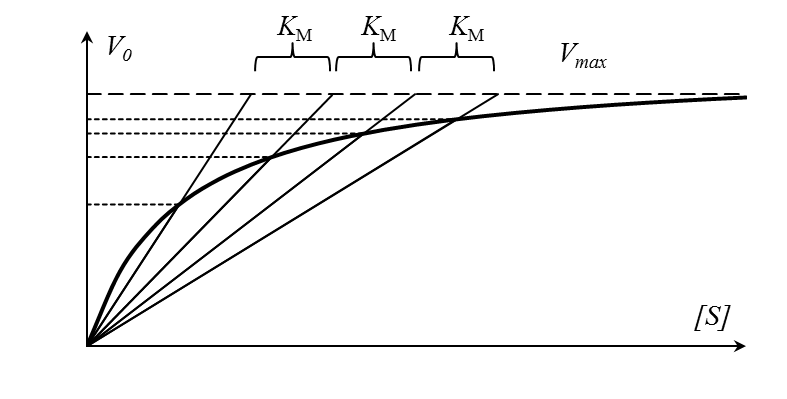 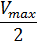 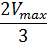 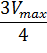 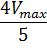 |
| Рисунок 5 – Определение КМ по методу Диксона. |
Анализируя графическим методом, проведем касательную к кривой в координатах уравнения Михаэлиса-Ментен. Для этого необходимо продифференцировать уравнение и подставить в полученную функцию значение концентрации в той точке, касательная к которой необходима – это точка (0;0), так что 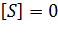
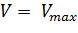
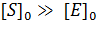
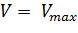
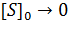
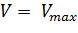
Видео:ФЕРМЕНТАТИВНАЯ КИНЕТИКА: Занятие 1. Вывод уравнения Михаэлиса-МентенСкачать

Кинетика и термодинамика ферментативных реакций (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 |
Министерство образования и науки Российской Федерации
Сибирский федеральный университет
Кинетика и термодинамика ферментативных реакций
к практическим занятиям
Специальность 020208.65 — Биохимия
Кинетика и термодинамика ферментативных реакций: Сборник задач к практическим занятиям /[Текст] / сост. . – Красноярск: Сиб. федер. ун-т, 2012. – 64 с.
Сборник задач по курсу «Кинетика и термодинамика ферментативных реакций» составлен в соответствии с программой курса и является учебно-методическим руководством по решению задач по кинетическим свойствам ферментов.
В учебном пособии представлены четко структурированные задачи по основному разделу курса «Кинетика ферментативных реакций» разной степени сложности. Предназначено для студентов биологических и медико-биологических специальностей университетов.
В ферментативной кинетике концепция стационарности применима к концентрациям связанных с ферментом интермедиатов. Когда фермент смешивается с избытком субстрата наблюдается начальный период, известный как предстационарное состояние, в течение которого концентрации этих интермедиатов достигают стационарного уровня. По достижении интермедиатами стационарных концентраций скорость реакции относительно медленно изменяется со временем и именно в данный период традиционно измеряют скорости энзиматических реакций.
Стационарное состояние является аппроксимацией, поскольку субстрат постепенно превращается в ходе эксперимента. Но, принимая во внимание, что измерения осуществляются за короткий промежуток времени, когда концентрация субстрата изменяется незначительно, стационарное состояние является хорошей аппроксимацией. Хотя изучение предстационарной кинетики позволяет анализировать механизмы ферментативного катализа, стационарная кинетика более важна для измерения каталитической активности фермента при стационарных состояниях в клетке.
Раздел 1. Уравнение Михаэлиса-Ментен
Браун (Brown A. J.) и затем В. Анри (Henri V.) в начале ХХ века высказали предположение о том, что в основе ферментативной реакции лежит обратимое взаимодействис субстрата с ферментом с образованием комплекса, который далее распадается с образованием продуктов реакции и регенерацией исходного фермента. Эта гипотеза была далее развита в работах Михаэлиса (L. Michaelis) и Ментен (M. L. Menten) (1913 г.) и позднее – Бригсом (G. E. Briggs) и Холденом (J. B.S. Haldane) (1925 г.).
Кинетическую схему простейшей односторонней ферментативной реакции превращения одного субстрата в продукт можно представить следующим образом:

Ферментативная реакция протекает в два этапа. На первом этапе фермент и субстрат образуют фермент-субстратный комплекс ES. Этот этап является быстрым и обратимым, он не сопровождается какими-либо химическими изменениями субстрата. Константы скорости реакции образования фермент-субстратного комплекса и обратного его распада равны соответственно k+1 и k-1. В образовании фермент-субстратного комплекса (ФСК, комплекс Михаэлиса) принимают участие нековалентные взаимодействия.
Каталитический процесс осуществляется на втором этапе реакции с константой первого порядка k+2 (kcat, число оборотов фермента). Комплекс Михаэлиса распадается с образованием конечного продукта реакции Р и регенерацией исходного фермента. Распад фермент-субстратного комплекса может происходить по-разному: в данной кинетической схеме он распадается в одну стадию, но в других случаях этих стадий может быть несколько.
Исходя из уравнения (1), можно расписать уравнения для скоростей отдельных стадий реакции.
Скорость образования фермент-субстратного комплекса:

Скорость обратной реакции (диссоциации комплекса на исходные вещества):

Скорость распада комплекса ES с образованием продуктов реакции и регенерацией фермента:

Стационарное течение процесса возможно тогда, когда концентрация субстрата существенно превосходит концентрацию фермента ([S]>> [E]). В этом случае распад комплекса ES по реакциям (+2) и (-1) уравновешивается его образованием по реакции (+1). Поэтому для условия стационарности можно записать:

Обозначив общую концентрацию фермента через [E]0, при условии, что [E]0 = [E] + [ES], преобразуем предыдущее уравнение

Откуда концентрация фермент-субстратного комплекса будет равна



Скорость ферментативной реакции, измеряемая согласно схеме (1) по образованию продукта реакции Р из комплекса ES, может быть выражена следующим образом

Подставляя в это выражение найденное значение [ES], получаем
Данное уравнение отражает зависимость скорости ферментативной реакции от концентрации фермента и субстрата. Константа Км носит название константы Михаэлиса и имеет размерность концентрации субстрата. Уравнение (2) свидетельствует, что зависимость скорости ферментативной реакции от концентрации субстрата при [E]0=const является гиперболической функцией (рис. 1.1).
Рис.1.1. Зависимость скорости ферментативной реакции от концентрации субстрата
Кривая представляет собой равнобочную гиперболу. При достаточно малых концентрациях субстрата, когда [S] > Км, можно принять, что Км + [S] ≈ [S], и тогда
а реакция имеет нулевой порядок по отношению к субстрату. Следовательно, при достижении определенной концентрации субстрата скорость ферментативной реакции достигает максимального значения Vmax и при дальнейшем увеличении концентрации субстрата не изменяется.
Смысл такого рода зависимости очевиден: скорость ферментативной реакции определяется в целом концентрацией фермент-субстратного комплекса и при малых концентрациях субстрата концентрация комплекса Михаэлиса пропорциональна [S], тогда как при избытке субстрата фактически весь фермент находится в форме ES. Дальнейшее повышение концентрации субстрата не приводит к увеличению [ES].
С учетом приведенного выше выражения, окончательное уравнение зависимости скорости ферментативной реакции от концентрации фермента и субстрата приобретает вид

Уравнение (3) является фундаментальным уравнением ферментативной кинетики и обычно называется уравнением Михаэлиса-Ментен.
Скорость реакции приближается к максимальной достаточно медленно, и даже при [S]= 10Км, величина скорости достигает только 0,91 Vmax. В связи с этим значение максимальной скорости очень часто трудно измеримо и его приходится рассчитывать из скоростей, наблюдаемых при концентрациях субстрата ниже насыщающих.
1.1. Характеристика кинетических констант
В уравнении Михаэлиса есть два кинетических параметра, имеющих важное значение для характеристики любого фермента. Это константа Михаэлиса и максимальная скорость реакции. Константа Михаэлиса определяется соотношением констант (k—1+k+2/k+1), а величина Vmax, называемая максимальной скоростью, ‒ произведением k+2 [E]0.
Константа Михаэлиса численно равна концентрации субстрата, при которой начальная скорость ферментативной реакции равна половине максимальной. Высокое сродство фермента к субстрату характеризуется низкой величиной Кm и наоборот, низкое сродство – высокой величиной Км.
Величина Vmax не является фундаментальной характеристикой фермента, поскольку зависит от его концентрации. Если концентрация фермента известна, то целесообразно ввести величину kcat – каталитическую константу (или число оборотов фермента), определяемую выражением Vmax/[E]0. Для механизма Михаэлиса kcat идентична k+2, однако в общем случае лучше пользоваться менее определенным обозначением, а именно kcat.
Константу kкат называют еще «числом оборотов» поскольку она соответствует числу молекул субстрата, превращаемых в продукт одной молекулой фермента за 1 с. Отношение констант kcat/Км называют константой специфичности фермента.
1.2. Методы определения Км и Vmax
Константу Михаэлиса можно определить из графика Михаэлиса (рис.1.1), найдя графическим способом максимальную скорость и соответствующую величину концентрации субстрата, при которой скорость ферментативной реакции будет вдвое меньше Vmax. Эта величина [S] и будет Км. Таким способом можно определить только приблизительную величину константы Михаэлиса из-за трудности точного графического определения Vmax.
Более удобными являются методы, в которых осуществлена линеаризация уравнения Михаэлиса-Ментен, т. е. гиперболическая зависимость v от [S] переведена в линейную.
Для того чтобы построить такой график, необходимо определить в одинаковых условиях при различных концентрациях субстрата и [E]= const начальные скорости ферментативной реакции.
Метод Лайнуивера-Берка. Один из способов линеаризации уравнения Михаэлиса-Ментен предложили Лайнуивер и Берк (Lineweaver H., Burk D.)). Это так называемый метод двойных обратных величин. Для линеаризации необходимо взять обратные величины от левой и правой частей уравнения (), в результате чего оно преобразуется в уравнение вида
согласно которому между величинами, обратными начальной скорости (1/v, v-1) и концентрации субстрата (1/[S], [S]-1) соблюдается линейная зависимость, если механизм реакции подчиняется изложенным выше представлениям (рис.1.2).
Рис. 1.2. График зависимости 1/v от 1/[S] (график Лайнуивера-Берка)
Экспериментальная прямая пересекает ось абсцисс в точке (-1/[S] = 1/Км), а ось ординат – в точке (1/v = 1/Vмах). Тангенс угла наклона равен Км/Vмах. Этим широко пользуются для определения параметров Км и Vмах, характеризующих связывающую и каталитическую функции ферментов.
Метод Хайнса-Вульфа. В этом случае преобразуется уравнение Лайнуивера-Берка путем умножения правой и левой частей на концентрацию субстрата.
Графическая зависимость приведена на рис.1.3.
Рис. 1.3. График зависимости [S]/v от [S] (график Хайнса-Вульфа)
Это прямая с наклоном 1/Vmax, отсекающая на осях [S]/v и [S] отрезки Км/ Vmax и – Км соответственно.
Метод Иди-Хофсти. При одном из таких графических преобразований в так называемом графике Иди-Хофсти (pиc.2.3.5) строят график зависимости v от v/[S]. В этом случае точка пересечения прямой, полученной путем наилучшей линейной аппроксимации экспериментальных точек, с осью ординат соответствует Vmax, а тангенс угла наклона равен – Km. Данный способ линеаризации приведен на рис. 1.4.
Рис. 1.4. График зависимости v от v/[S] (график Эди-Хофсти)
Метод Эйзенталя и Корниш-Боудена. Много позднее Эйзенталь и Корниш-Боуден предложили иной метод графического представления результатов исследования кинетики ферментативных реакций – так называемый прямой линейный график. Уравнение Михаэлиса-Ментен они преобразовали в виде зависимости Vmax от Км:
Для любой пары значений [S] и v можно построить зависимость Vmax от Км. Она представляет прямую с наклоном, равным v/[S], и отрезками, отсекаемыми на осях Км и Vmax, соответственно равными – [S] v. Если провести прямые для нескольких пар значений [S] и v, то эти прямые пересекутся в одной точке, координаты которой дадут единственные значения Vmax от Км, удовлетворяющие всем парам значений [S] и v (рис.1.5).
Рис.1.5. Определение кинетических констант – Км и Vmax по методу Эйзенталя и Корниш-Боудена
Преимущества такого графика очевидно: для его построения не требуется никаких расчетов, он позволяет очень просто выявить ошибочные данные (такие прямые будут выпадать из основной совокупности прямых).
Уравнение Михаэлиса лежит в основе всех кинетических исследований ферментативных реакций, так как оно позволяет рассчитать количественные характеристики ферментов и проводить анализ их ингибирования. Величины Кm и Vmax являются важнейшими характеристиками ферментов и их можно определить, используя линеаризованные формы уравнения Михаэлиса-Ментен.
Графические методы для определения Vmax и Кm не являются оптимальными. В настоящее время данные ферментативной кинетики обрабатывают быстрее и более объективно с помощью компьютерных программ.
1.3. Задачи к разделу 1
Задача 1.1.. Определить кинетические параметры реакции, катализируемой фосфоглюкомутазой, исходя из данных, приведенных в табл.1.
🎬 Видео
USMLE Step 1 - Фармакология: кинетика ферментов | уравнение Михаелиса - Ментена и не толькоСкачать

Ферментативная кинетикаСкачать

ФЕРМЕНТЫ 5.Основы ферментативного катализа. Кинетика ферментативных реакций.Скачать

Асеев В. В. - Основы энзимологии - Ферментативная кинетика Уравнение Михаэлиса-МентенСкачать
Кто выше? - Люси хочет быть выше!! | Мультфильм Для Детей | Повседневная история ребенкаСкачать

Кинетика. О чем говорят графики. БиохимияСкачать

Конвейер для младенцев - Дженни превращается во множество материалов | Мультфильм Для ДетейСкачать

Lucy на русском | Волшебный пульт дистанционного управления | Мультфильм для детейСкачать

Не оставляйте Люси, Вулфу и мамочку! - Малыш попал в больницу | Мультик для детей | Wolfoo RussianСкачать

Lucy на русском | О нет, не смейся над Люси! - Люси нужно на горшок | Мультики для детейСкачать

Lucy на русском | Незнакомец в больнице | Мультфильм для детейСкачать

Lucy на русском | Не бойся, детка! - Первый Раз У Доброго Доктора 💊 | Мультфильм для детейСкачать

Lucy на русском | Не бойся, малыш-солдат!!! Люси делают прививку | Мультики для детейСкачать

Биохимия. Лекция 22. Ферменты. Part 2.Скачать

Lucy на русском | Люси показывает правила безопасности в бассейне | Мультфильм для детейСкачать

Lucy на русском | Первый день в школу - Никто не хочет играть с Люси | Мультфильм для детейСкачать