- Евгений Перхуров 5 лет назад Просмотров:
1 1 Направления подготовки: Авионика Аэронавигация Системная инженерия Бортовые системы управления Дисциплина: Курс, семестр, уч. год: 3, весенний, 11/1 Кафедра: 31 СУЛА Руководитель обучения: ассистент Копысов Олег Эдуардович ЛЕКЦИЯ 3 ТЕМА: УРАВНЕНИЯ ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА КАК ТВЕРДОГО ТЕЛА. ПРОДОЛЬНОЕ И БОКОВОЕ ДВИЖЕНИЕ Движение ЛА, как твѐрдого тела в связанной системе координат описывается уравнениями Эйлера (шесть нелинейных дифференциальных уравнений второго порядка). Силы и моменты, входящие в эти уравнения, сложным образом зависят от высоты, скорости и режима полѐта и меняются во времени, г. к. изменяются условия полѐта, например из-за изменения массы и момента инерции ЛА в результате расхода топлива или сброса груза. При аналитическом исследовании процессов управления ЛА его уравнения движения, как правило, упрощают, рассматривая два независимые друг от друга движения: продольное и боковое. К продольному относят поступательные движения ЛА вдоль осей ОХ и ОY и вращательное движение вокруг оси O. К боковому движению относят поступательное вдоль оси O и вращательные движения вокруг осей ОХ и ОY. Продольное движение. Обобщенная математическая модель При продольном движении ЛА вектор V линейной скорости его центра масс находится в вертикальной плоскости. Внешние силы, действующие на ЛА: Р сила тяги двигателей, вектор которой направлен вдоль оси ОХ: Х а сила лобового сопротивления, вектор которой направлен против вектора V, т.е. в отрицательную сторону оси ОХ а Y а подъѐмная сила, вектор которой перпендикулярен вектору V mg вес ЛА (m масса ЛА, g ускорение свободного падения). Вращение ЛА в плоскости
2 Х а Y а возможно под действием момента М, действующего вокруг оси O а, который называется аэродинамическим моментом тангажа. В соответствии с рис. 3.1 имеют место кинематические соотношения:, (3.1) где ϑ угол тангажа θ угол наклона траектории движения центра масс (ЦМ) ЛА ω угловая скорость тангажа. Рисунок 3.1 Внешние силы, действующие на ЛА в продольном движении Вращательное движение ЛА вокруг оси O а описывается уравнением: I, (3.) где I момент инерции ЛА относительно оси O а М момент аэродинамических сил, который можно представить в виде: mba S V, (3.3) где т коэффициент момента b а — хорда крыла ρ плотность воздуха S площадь крыльев. Коэффициент т можно представлять состоящим из суммы трех слагаемых, два из которых зависят от статических параметров (α, V, δ в ) и определяют статический момент, а третий от динамических параметров ( ), и определяет демпфирующий момент.
3 3 Спроектируем силы, действующие на ЛА, на касательную к траектории полѐта (ось X) и на нормаль к ней (ось Y). Сумма проекций сил на касательную к траектории: dv m mv P cos X a mg sin. dt (3.4) При определении проекций сил на нормаль к траектории нужно иметь в виду, что при движении ЛА по искривленной траектории с радиусом кривизны r, на него действует центробежная сила инерции mv траектории), a ds = Vdt, то / mv mv mv d r. Так как r = ds/dθ (s длина дуги mv mv. r ds / d Vdt / d dt Следовательно, сумма проекций сил на нормаль к траектории: mv Y Psin mg cos. a (3.5) Сила тяги Р зависит от параметров двигателя, от внешних условий, характеризуемых скоростью полѐта V, высотой полѐта Н и параметра управления двигателем δ р, т. е. в общем виде Р = Р(V, Н, δ р ). Аэродинамические силы Х а и Y а зависят от угла атаки α, скорости полѐта V, плотности воздуха ρ и угла отклонения руля высоты δ в. Так как угол δ в практически не влияет на величины Х а и Y а, то этим влиянием пренебрегают и представляют их обычно в виде: где X a CxaS V Ya CyaS V, (3.6) C xa, C ya коэффициенты лобового сопротивления и подъемной силы, зависящие от угла атаки и скорости полета. Система нелинейных дифференциальных уравнений (3.), (3.4), (3.5) с учѐтом (3.1), (3.3), (3.6) является математической моделью продольного движения ЛА. Известно, что для пилотируемых ЛА самолетной схемы практически для всех компоновок и большинства режимов полета, собственное движение ЛА состоит из двух колебательных движений, отличающихся частотой и степенью затухания. Эти движения называются короткопериодическими и длиннопериодическими или фуго-
4 идными. Причиной возникновения короткопериодических движений является нарушение равновесия моментов вокруг оси O a, что приводит к вращению ЛА относительно ЦМ и изменению углов α и ϑ. Скорость невозмущѐнного линейного движения при этом практически не изменяется. Причиной возникновения длиннопериодических движений является нарушение внешних сил, действующих в продольной плоскости симметрии ЛА, следствием чего является изменение скорости его полета. 4 Линеаризованные уравнения продольного движения ЛА Применяя к уравнениям (3.), (3.4), (3.5) метод малых возмущений, могут быть получены линейные уравнения продольного движения ЛА. Предположим, что на исследуемом участке полета невозмущенное движение ЛА характеризуется постоянными силами X, Y, P, и параметрами V, α, ϑ, θ, H и ω z =, а параметры управления δ В, δ р также постоянны. Если исследуется участок полета, на котором параметры движения существенно меняются, его разбивают на несколько участков, на которых параметра движения можно считать постоянными. Уравнения невозмущѐнного движения ЛА на участке с постоянными параметрами следуют из уравнений (3.), (3.4), (3.5): P cos X mg sin Y P sin mg cos. Из первых двух уравнений системы следует отношение: P cos X tg, P sin Y (3.7) из которого можно заключить, что при P cos X ЛА летит горизонтально, при P cos X набирает высоту ( ), а при P cos X уменьшает высоту ( ).
5 Если в некоторый момент времени параметры движения и управления изменились на величины V. то соответствующие параметры P возмущѐнного движения принимают вид: V V V P P P. При изучении продольного углового движения ЛА в области малых изменений параметров движения первое уравнение системы (3.7) из рассмотрения можно исключить, т.к. оно представляет сумму проекций сил на ось ОХ a (рис. 3.1), не влияющих на угловое движение ЛА. При линеаризации второго уравнения системы (3.7) полагают, что проекция силы тяжести на ось OY a не оказывает влияния на угловое движение ЛА, и этой составляющей можно пренебречь. В результате известных процедур линеаризации могут быть получены простейшие уравнения продольного движения ЛА: mv Y I (3.8), где постоянные коэффициенты соответствуют исходному невозмущѐнному движению и определяются следующим образом: Y Y ( Pcos ) ( ) ( ) ( ). 5
6 Рассмотрим аэродинамические моменты в уравнениях (3.8), определяющих короткопериодическое движение ЛА. При >, что обычно имеет место, момент называется моментом продольной статической устойчивости, который является следствием воздействия набегающего воздушного потока на хвостовое горизонтальное оперение, от размеров и формы которого главным образом и зависит. При невозмущѐнном движении ЛА угол атаки и аэродинамический момент относительно поперечной оси отсутствует. Восходящие или нисходящие потоки воздуха приводят к изменению угла атаки на величину например изменения центровки ЛА. Величина, который может измениться и из-за других причин, приводит к увеличению подъѐмной силы крыльев, следствием чего является изменение высоты полѐта ЛА, и к увеличению на Y подъѐмной силы горизонтального хвостового оперения, которая приложена в центре давления (ЦД) на плече L ГО, что и создаѐт момент Y L ГО, возвращающий ЛА к прежнему углу атаки, т.е. (рис. 3.). Таким образом, момент обеспечивает продольную устойчивость ЛА, если центр давления аэродинамических сил находится за центром масс ЛА в сторону хвостового оперения. Если ЦМ и ЦД совпадают, то 6 = (нейтральный ЛА), если ЦД находится впереди ЦМ, то 7 еѐ увеличение средствами аэродинамики приводит к увеличению воздействия на ЛА аэродинамических возмущений. 7 Рисунок 3. Определение момента продольной статической устойчивости Рисунок 3.3 Определение момента демпфирования тангажа Управляющий момент появляется при отклонении руля высоты хвостового горизонтального оперения, вследствие чего изменяется его угол атаки. Физическая картина воздействия этого момента на ЛА аналогична влиянию момента продольной статической устойчивости (статической устойчивости тангажа). На руль высоты, отклонѐнный от нейтрального положения на угол, действует аэродинамическая сила Y РВ, направленная перпендикулярно набегающему потоку воздуха и приложенная в ЦД рулевой поверхности (рис. 3.4), который, как правило, не совпадает с ее осью вращения (ОВ). Сила Y РВ относительно оси вращения создает так называемый шарнирный момент, который является основным нагрузочным моментом для привода, осуществляющего разворот руля высоты. В точке, соответствующей ОВ, можно приложить две противоположно направленных силы Y РВ, равных по модулю Y РВ.
8 8 Рисунок 3.4 Определение управляющего момента по высоте Тогда можно записать равенство, Y ‘ L Y ‘ l Y L из которого P P P P следует, что управляющий момент, приложенный к ЛА, состоит из суммы шарнирного момента, действующего относительно ОВ руля и момента силы Y РВ на плече L относительно ЦМ ЛА. Вернемся к уравнениям системы (3.8) и перепишем их в переменных приращений углов тангажа где и атаки : I mv ( ) Y F. Y (3.9), F Y возмущающие момент и сипа, действующие соответственно относительно оси O а и вдоль оси OY а. Уравнения системы (3.9) перепишем в виде: где a1 a a3 a a a a a 5 a F, 6 Y Y. a I I I 4 1, a 1 5, a6. I mv mv (3.1) (3.11) Постоянные коэффициенты в (3.11), соответствующие невозмущѐнному движению, определяются следующим образом:
9 m qsb m qsl m qsb Y c, yqs (3.1) где q V / скоростной напор b хорда крыла. 9 Боковое движение Аэродинамические силы и моменты, действующие на ЛА Боковое движение ЛА включает вращение вокруг продольной оси ОХ, нормальной оси ОY и линейное перемещение вдоль оси O. Рассмотрим основные аэродинамические силы и моменты, действующие на ЛА (рис. 3.5). Предположим, что вследствие какого-либо возмущения ЛА относительно нормальной системы координат ОХ g Y g g получил крен на угол γ, после чего возмущение исчезло. Угол γ определяет положение связанной системы координат ОХY, причѐм т. О совпадает с центром масс ЛА самолѐтной схемы. Плоскости крыльев относительно плоскости Х располагаются под углом φ. При положительном крене (на правое крыло) вдоль оси O появляется составляющая mg sin силы веса ЛА, под действием которой возникает скольжение ЛА со скоростью V VXtg ( V X продольная составляющая скорости V, β угол скольжения). Вследствие скольжения нарушается симметрия обтекания крыльев воздушным потоком. Для иллюстрации указанного обстоятельства на концах правого и левого крыльев построены треугольники воздушных скоростей ( V к составляющая скорости V набегающего воздушного потока вдоль крыльев V I — составляющая, перпендикулярная вектору скорости V ), из которых следует VI V tg. Так как скорости V 1 на правом и левом крыльях направлены в разные стороны, происходит изменение их углов атаки, что иллюстрируется построением треугольников скоростей на векторах скоростей V X и V I, из которых следует V / V. При этом на правом крыле имеет место положительное приращение I X угла атаки (+ ), а на другом отрицательное ( ).
10 1 Рисунок 3.5 Определение моментов статической устойчивости крена и пути Соответственно подъемная сила правого крыла увеличится на ΔY, а левого уменьшится на ΔY. В результате относительно оси ОХ образуется момент поперечной статической устойчивости или момент статической устойчивости крена, первопричиной которого является скольжение и который обозначается в виде, х М где ( х ) х. Очевидно, что этот момент тем больше, чем больше изменение угла, величина которого в соответствии с приведенными выше соотношениями, может быть представлена в виде: VI Vtg Vxtgtg, V V V x x x откуда следует, что чем больше угол φ, тем больше момент поперечной устойчивости. Стреловидность крыльев в плане также приводит к появлению момента поперечной устойчивости. Изменение углов атаки приводит к изменению сил лобового сопротивления на крыльях: на правом крыле эта сила увеличится на величину ΔХ, а на левом умень-
11 шится на ΔХ. С появлением угла β возникает также сила Δ на вертикальном оперении. Следствием указанных сил является возникновение флюгерного момента, или момента статической устойчивости пути, который старается развернуть ЛА в сторону набегающего воздушного потока. Этот момент обеспечивает устойчивость по углу скольжения, стремясь так развернуть ЛА, чтобы установился угол скольжения, имевший место до возмущения. Момент статической устойчивости пути обозначается в виде, где ( М y ) y y. 11 Используя литературные источники, найти графические зависимости коэффициента продольного момента от угла атаки и отклонения руля высоты, зависимость коэффициентов С ха, С уа от угла атаки. Термины для занесения в тезаурус: продольное движение, боковое движение, коэффициент лобового сопротивления, коэффициент подъемной силы, невозмущенное движение летательного аппарата, момент статической устойчивости, шарнирный момент.
- ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ВОЗМУЩЕННОГО ДВИЖЕНИЯ САМОЛЕТА
- Курсовая работа: Расчёт закона управления продольным движением самолета
- 1.1 Общие сведения
- 1.2 Уравнения продольного движения самолета
- 1.3 Силы и моменты при продольном движении
- 1.4 Линеаризованные уравнения движения
- 1.5 Математическая модель привода стабилизатора
- 1.6 Математические модели датчиков угловой скорости и перегрузки
- 1.7 Математическая модель датчика положения штурвала
- 2.1 Общие положения
- 2.2 Требования к статическим характеристикам
- 2.3 Требования к динамическим характеристикам
- 2.4 Требования к разбросам параметров
- 2.5 Дополнительные требования
- 3.1 Этап анализа
- 3.2 Этап синтеза
- 📹 Видео
Видео:АУПО. Математическая модель продольного движения. ЛинеаризацияСкачать

ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ВОЗМУЩЕННОГО ДВИЖЕНИЯ САМОЛЕТА
Прежде чем перейти к линеаризации уравнений возмущенного движения самолета (15.1), рассмотрим методику линеаризации нелинейных дифференциальных уравнений возмущенного движения произвольной динамической системы (см. 9.1)
Пусть невозмущенному (опорному) движению соответствует одно из частных решений уравнений (15.2) вида ys = у® (t). Подставляя это частное решение в (15.2), получим следующие равенства, отвечающие опорному движению,
)о ** + («ПН*у*+- + (ж)о Дг/» + ( …. asn =
Коэффициенты уравнений (15.7) будут переменными в случае неустановившегося невозмущениого движения и постоянными, когда невозмущенйое движение установившееся.
 |
В соответствии с изложенной методикой линеаризации будем считать, что кинематические параметры возмущенного движения
самолета мало отличаются от параметров опорного движения в одни и те же моменты времени: V — V0 + AV, а = а0 + Да, •••, х =
Здесь V0, а0, …, со£, … — параметры опорного (невозмущенного) движения; AV, Да, …, Асо% … — мальїе отклонения параметров возмущенного движения от их значений в опорном дгпжении.
— Условие малости угловых отклонений Ах позволяет принять cos Ах « 1, a sin Ах « Ах, где х : а, р, G, …
При линеаризации уравнений (15.1) будем пренебрегать произведениями малых отклонений как величинами рыше первого порядка малости.
Правые части уравнений 1—3 и 7—9 системы (15.1) разложим в ряды Тейлора по степеням отклонений (AV, Аа, …) в окрестности невозмущенного движения, сохранив при этом только величины первого порядка малости.
В качестве примера рассмотрим линеаризацию первого уравнения системы (15.1). Принимая массу самолета постоянной, получим
Так как в невозмущеином движении справедливо равенство т = Д®к, то линейное дифференциальное уравнение примет вид
+ Д0 + РІЇ дев 4- F6« ден + FPXK АР.. .,

Подобным образом можно провести линеаризацию остальных уравнений системы (15.1).
Обращаем внимание на то, что вид линеаризованных уравнений н значения коэффициентов FXK> F°^t… зависят от выбранного опорного (невозмущенного) движения, относительно которого рассматриваются отклонения AV, Да, Ар, …
Нл; Наиболее простым, но достаточно характерным является случай, когда в качестве опорного рассматривается прямолинейный устано — . вившийся полет без крена и скольжения. В этом движении V0 = = const; а0 = const; 0° = const; 4го = ф° = const; (Ї0 = у° = у ° = = 0; со£ — сор = со® = 0; 6“ = 6£ = 0 и, следовательно, F%K = 0; FIк = 0; fjк = 0; М%х — 0; М%у = 0и М%г = 0.
При линеаризации будем предполагать, что направление нормальной оси OXg выбрано таким образом, что в невозмущенном дви-
жении углы пути и рыскания 4го и |з° являются малыми величинами. Кроме того, приближенно будем считать, что влияние приращения высоты АН в возмущенном движении на аэродинамические силы и моменты и на тягу двигателей мало и учитывать его не будем.
После линеаризации уравнений (15.1) система линейных дифференциальных уравнений возмущенного движения самолета принимает вид
mAV = FvXKAV + F? KAa — h fH« ДЄ + ft АР+
+ FXK АР + FlBK A6b — f Fl»K A6„ + ..’., mV° A0 = Fh AV + * A-x + f]k Д0 + Др + f£ AP + F^ A6B — f
tnV° cos G° AW=FVZK AV + F°ZKAa + FZK Др + fJ? Aya + F% A6„ f • •
AL = cos G°AV — V° sin G°AG;
AH = sin G°AV + V° cos 0°AG;
Jx A(ox — Jxy A&y = Мд* AV + Мд* Ad y -)- Мд* A6H -(- Мд* Д6* — j — ..
JyAtiy — Jxy Av)x — M-Ry A К Мцу Да — f» Ap — f — Мд^ Aw* -(-
+ Mfty Atoу -f — Мд” A6H -)- Мд°Д6, -b • • • •
Jt Дев, = Мд, ДК + M д, Аа + Лід, Др + Мд, Да + Мд| Ato* — f-
+ Мд, АР + M& Двн + Л1д5 Д6В + .
 |
Если в качестве опорного движения рассматривать неустановив — шийся прямолинейный полет, то коэффициенты в уравнениях (15.8) будут переменными, а в случае установившегося — постоянными.
Полученную сложную систему линейных дифференциальных уравнений (15.8) можно разделить на простые подсистемы, которые можно исследовать независимо друг от друга.
Видео:Теория автоматического управления. Лекция 5. Гармоническая линеаризацияСкачать

Курсовая работа: Расчёт закона управления продольным движением самолета
| Название: Расчёт закона управления продольным движением самолета Раздел: Рефераты по транспорту Тип: курсовая работа Добавлен 16:15:05 05 декабря 2010 Похожие работы Просмотров: 129 Комментариев: 23 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать |

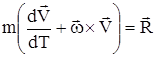 ,
,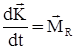 ,
,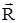 – равнодействующая всех сил;
– равнодействующая всех сил;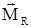 – главный момент внешних сил самолёта, вектор суммарного вращающего момента;
– главный момент внешних сил самолёта, вектор суммарного вращающего момента;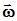 – вектор угловой скорости системы координат;
– вектор угловой скорости системы координат;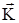 – момент количества движения самолёта;
– момент количества движения самолёта;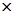 » обозначает векторное произведение. Далее переходят к обычной скалярной записи уравнений, проектируя векторные уравнения на некоторую систему координатных осей.
» обозначает векторное произведение. Далее переходят к обычной скалярной записи уравнений, проектируя векторные уравнения на некоторую систему координатных осей.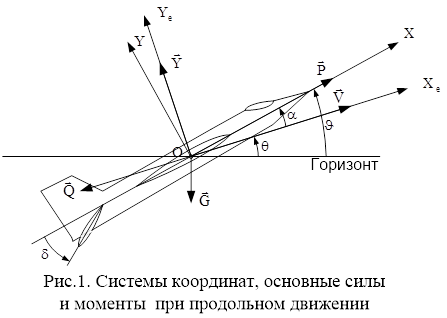
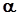 – угол атаки,
– угол атаки, 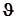 – угол тангажа,
– угол тангажа, 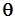 – угол наклона траектории,
– угол наклона траектории, 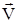 – вектор воздушной скорости,
– вектор воздушной скорости, 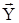 – подъемная сила,
– подъемная сила, 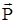 – сила тяги двигателей,
– сила тяги двигателей, 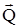 – сила лобового сопротивления,
– сила лобового сопротивления, 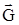 – сила тяжести,
– сила тяжести, 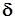 – угол отклонения рулей высоты,
– угол отклонения рулей высоты, 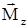 – момент тангажа, вращающий самолёт вокруг оси ОZ.
– момент тангажа, вращающий самолёт вокруг оси ОZ.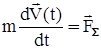 , (1)
, (1)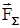 – суммарный вектор внешних сил. Представим вектор скорости с использованием его модуля V и угла его поворота
– суммарный вектор внешних сил. Представим вектор скорости с использованием его модуля V и угла его поворота 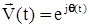 .
.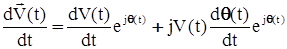 . (2)
. (2)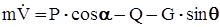 ; (3)
; (3)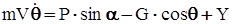 . (4)
. (4)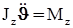 , (5)
, (5)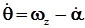 , (6)
, (6)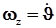 – (7)
– (7)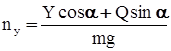 . (8)
. (8)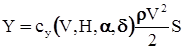 ; (9)
; (9)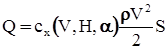 . (10)
. (10)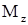 есть функция скорости V и высоты H полёта, угла атаки
есть функция скорости V и высоты H полёта, угла атаки 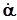 , угловой скорости изменения угла тангажа (скорости вращения
, угловой скорости изменения угла тангажа (скорости вращения 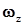 самолёта вокруг связанной поперечной оси OZ) и угла отклонения руля высоты
самолёта вокруг связанной поперечной оси OZ) и угла отклонения руля высоты 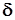 :
: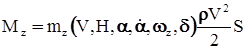 . (11)
. (11)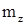 – задаваемые табличным путём функции,
– задаваемые табличным путём функции, – плотность атмосферы,
– плотность атмосферы,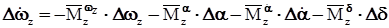 (12)
(12)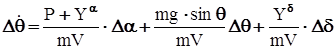 (13)
(13)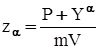 ;
; 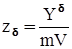 (14)
(14)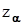 и
и 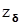 являются чрезвычайно информативными с точки зрения оценки режима полёта и качества угловых процессов самолёта. Пренебрежём, как это часто делается для маневренных самолётов, слагаемым
являются чрезвычайно информативными с точки зрения оценки режима полёта и качества угловых процессов самолёта. Пренебрежём, как это часто делается для маневренных самолётов, слагаемым 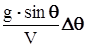 в правой части уравнения (13). С учётом равенства (6) получим уравнение для производной приращения угла атаки:
в правой части уравнения (13). С учётом равенства (6) получим уравнение для производной приращения угла атаки: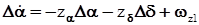 (15)
(15)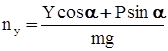 (16)
(16)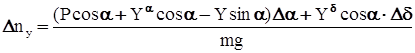 (17)
(17)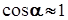 и пренебрегая величиной
и пренебрегая величиной 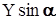 , с учётом (14) для углов, измеряемых не в радианах, а в градусах, получим:
, с учётом (14) для углов, измеряемых не в радианах, а в градусах, получим: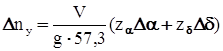 . (18)
. (18)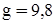 м/с 2 .
м/с 2 .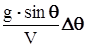 , получим формулу для приращения ускорения самолёта по оси подъёмной силы:
, получим формулу для приращения ускорения самолёта по оси подъёмной силы: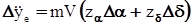 . (19)
. (19)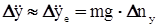 . (20)
. (20)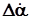 выражением (15), получим следующие уравнения состояния:
выражением (15), получим следующие уравнения состояния: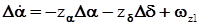 , (21)
, (21)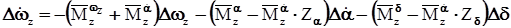 , (22)
, (22)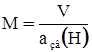 , (23)
, (23)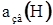 – скорость звука на данной высоте.
– скорость звука на данной высоте.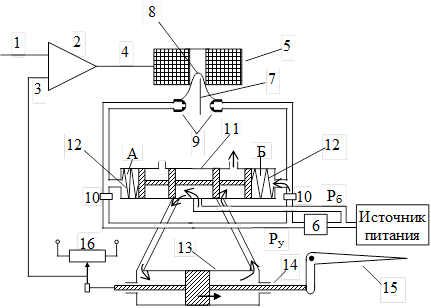
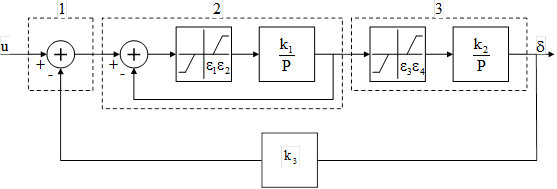
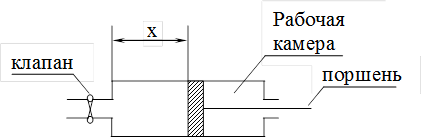
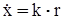 , (24)
, (24) .
.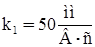 ,
, 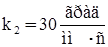 ,
,  ,
, 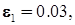
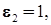
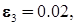
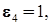 угол наклона нелинейных характеристик равен 45 0.
угол наклона нелинейных характеристик равен 45 0.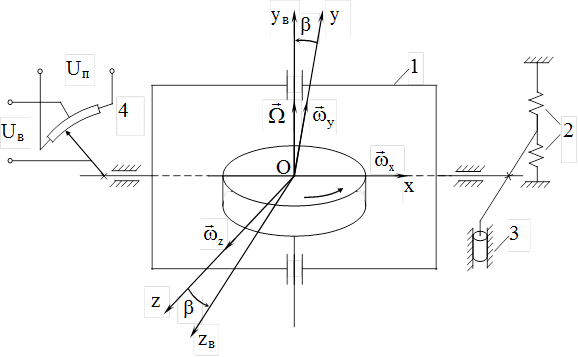 Рис. 5. Упрощенная схема демпфирующего гироскопа: 1 – двухстепенной гироскоп; 2 – пружина; 3 – демпфер; 4 – потенциометрический датчик.
Рис. 5. Упрощенная схема демпфирующего гироскопа: 1 – двухстепенной гироскоп; 2 – пружина; 3 – демпфер; 4 – потенциометрический датчик.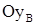 с большой угловой скоростью
с большой угловой скоростью  . в этом случае ротор гироскопа обладает большим кинетическим моментом
. в этом случае ротор гироскопа обладает большим кинетическим моментом 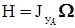 , где
, где 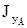 – момент инерции ротора гироскопа относительно оси
– момент инерции ротора гироскопа относительно оси 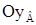 . Пусть Jx – момент инерции гироскопа вместе с рамкой относительно оси Ox. Тогда уравнение моментов относительно оси Ox имеет следующий вид:
. Пусть Jx – момент инерции гироскопа вместе с рамкой относительно оси Ox. Тогда уравнение моментов относительно оси Ox имеет следующий вид: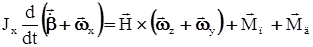 *) , (25)
*) , (25)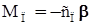 , (26)
, (26)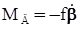 , (27)
, (27)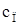 – жесткость пружины, f – коэффициент демпфирования, получим
– жесткость пружины, f – коэффициент демпфирования, получим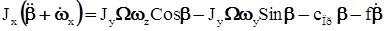 . (28)
. (28)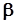 малой, пренебрегая величиной
малой, пренебрегая величиной 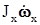 по сравнению с
по сравнению с 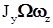 , поскольку величина скорости вращения гироскопа велика, и введя обозначения
, поскольку величина скорости вращения гироскопа велика, и введя обозначения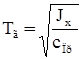 ,
, 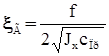 ,
, 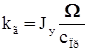 , (29)
, (29)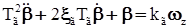 . (30)
. (30)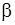 , то окончательно получим следующее выражение передаточной функции демпфирующего гироскопа:
, то окончательно получим следующее выражение передаточной функции демпфирующего гироскопа: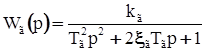 . (31)
. (31)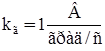 ,
, 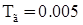 с,
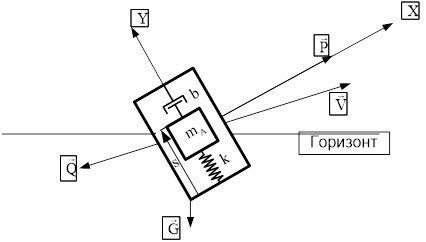
с, 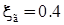 .
.
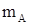 , имеющей возможность перемещаться в направляющих, параллельных оси пружины. Эти направляющие определяют ось чувствительности прибора.
, имеющей возможность перемещаться в направляющих, параллельных оси пружины. Эти направляющие определяют ось чувствительности прибора.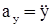 этого ускорения, то сумма сил, действующих на массу
этого ускорения, то сумма сил, действующих на массу 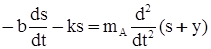 , (32)
, (32)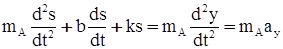 .*) (33)
.*) (33)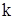 — жёсткость пружины,
— жёсткость пружины, 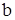 — коэффициент успокоительного демпфера. Изменение положения подвижной массы акселерометра
— коэффициент успокоительного демпфера. Изменение положения подвижной массы акселерометра 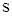 фиксируется потенциометрическим или индукционным линейным датчиком. Таким образом, передаточная функция акселерометра, определяемая как отношение изображений по Лапласу электрического выходного сигнала акселерометра к нормальному ускорению самолёта при нулевых начальных условиях, записывается следующим образом:
фиксируется потенциометрическим или индукционным линейным датчиком. Таким образом, передаточная функция акселерометра, определяемая как отношение изображений по Лапласу электрического выходного сигнала акселерометра к нормальному ускорению самолёта при нулевых начальных условиях, записывается следующим образом: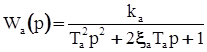 . (34)
. (34)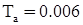 с,
с, 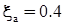 ,
, 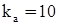 В/ед.
В/ед.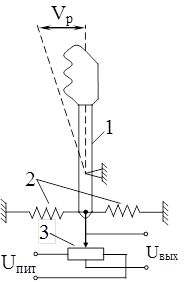
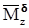 в пределах ±20%.
в пределах ±20%.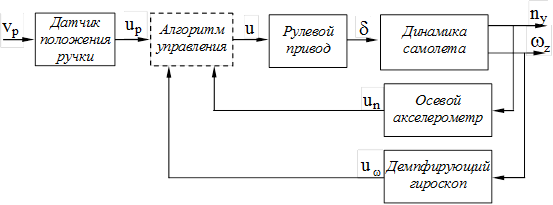
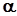 , а также до сигналов перегрузки
, а также до сигналов перегрузки 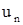 , и угловой скорости тангажа
, и угловой скорости тангажа 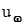 . Определить полюсы и нули всех передаточных функций.
. Определить полюсы и нули всех передаточных функций.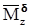 в уравнениях объекта помимо всего прочего накладывает и ограничения на выбор желаемых собственных значений наблюдателя.
в уравнениях объекта помимо всего прочего накладывает и ограничения на выбор желаемых собственных значений наблюдателя.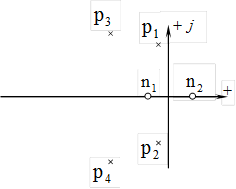
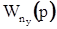 можно воспользоваться разложением
можно воспользоваться разложением 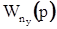 на элементарные дроби:
на элементарные дроби: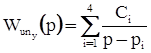 . (35)
. (35)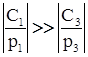 (часто это условие выполняется, когда
(часто это условие выполняется, когда 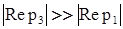 ). Тогда можно приближенно записать:
). Тогда можно приближенно записать: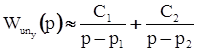 . (36)
. (36)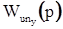 .
.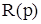 является полиномом числителя разомкнутой системы по перегрузке и не зависит от обратных связей и, следовательно, от желаемых собственных значений.
является полиномом числителя разомкнутой системы по перегрузке и не зависит от обратных связей и, следовательно, от желаемых собственных значений.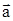 и
и 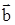 (обозначается
(обозначается 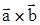 ) называется вектор
) называется вектор 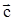 , длина которого равна произведению absinj (j — угол между векторами
, длина которого равна произведению absinj (j — угол между векторами 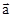 ,
, 
















