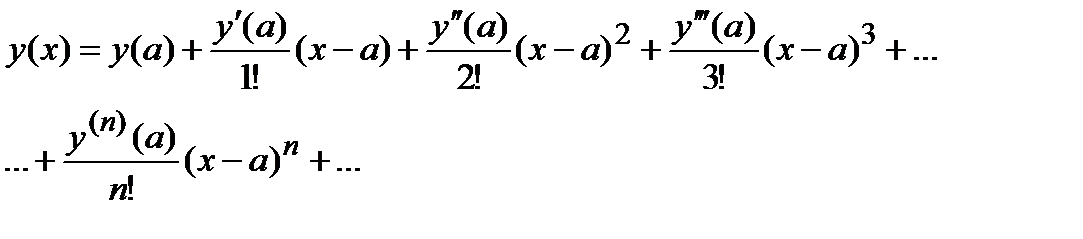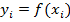В этом случае функция y(x) раскладывается в ряд Тейлора в окрестности точки a (рис.1,б):
с отбрасыванием всех членов высшего порядка малости (в этом и состоит линеаризация): 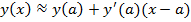 , (2) , (2) |
где 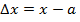
Второе слагаемое в (2) – дифференциал функции y(x) в точке a.
Пример.Исходная математическая модель является квадратным трехчленом:
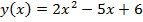
Необходимо линеаризовать эту модель в окрестности точки x=2.
Решение. По (3) находим: 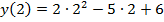
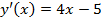
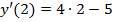
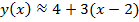
Сравним результаты расчетов по формулам (3) и (4):
| x | 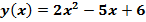 | 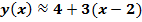 | Относительная погрешность,% |
| 2.01 | 4,03 | 4,03 | |
| 2,04 | 4,123 | 4,12 | 0,07 |
| 2,1 | 4,32 | 4,3 | 0,46 |
| 2,5 | 5,5 | 8,3 |
Как видим, при малых отклонениях погрешности получаются незначительными.
К тому же, модель (4) проще, чем (3), но недостатком такого подхода является необходимость пересчета коэффициентов (фактически построение другой модели) при существенном изменении значения x (например, при x=3).
Линейная регрессия
Общие положения
Как мы видели, математическая статистика занимается обработкой данных, полученных в результате какого-либо эксперимента. В частности – это зависимость величины Y от величины X в виде набора точек на плоскости (xi, yi), i = 1, …, n (рис.3). Но эта зависимость не будет однозначной (т.е. функциональной), а будет вероятностной (или стохастической), поскольку в общем случае и Y и X – случайные величины.
Функциональные связи являются абстракциями, в реальной жизни онивстречаются редко, но находят широкое применение в точных науках и впервую очередь, в математике. Например: зависимость площади круга отрадиуса: S=π∙r 2
Обычно при стохастической зависимости между X и Y одна величина рассматривается как независимая (X), а вторая (Y) – как зависимая от первой, и зависимая величина ведет себя как случайная величина и ее можно описать некоторым вероятностным законом распределения.
Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения.
Учитывая специфику вероятностной связи, эти величины (точнее – признаки) чаще называют факторными (которые обуславливают изменения других), или просто факторами, и результативными(которые изменяются под действием факторных признаков).
| x |
| y |
| Рис.3 |
Возникновение понятия стохастической зависимости обусловливается тем, что величины подвержены влиянию неконтролируемых или неучтённых факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками.То есть изучаемая система переходит не в определенное состояние, а в одно из возможных для нее состояний. Стохастическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения.
Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
Поэтому при проведении того же эксперимента мы могли бы получить и несколько другой набор пар (xi, yi) (точки красного цвета нарис.4) в силу именно случайности фигурирующих в эксперименте величин.
| X |
| Y |
| Рис.4 |
Это можно интерпретировать, что рис.3, например, является своего рода «фотографией», а на самом деле точки (xi, yi), в силу случайных факторов, могут занимать и другое место на графике.
Модель стохастической связи может быть представлена в общем виде уравнением: ŷi = ƒ(xi) + ei, где:
- f(xi)-часть результативного признака, сформировавшаяся под воздействием учтенных известных факторных признаков (одного или множества), находящихся в стохастической связи с признаком;
- ŷi-расчетное значение результативного признака;
- ei-часть результативного признака, возникшая вследствие действия неконтролируемых или неучтенных факторов, а также измерения признаков, неизбежно сопровождающегося некоторыми случайными ошибками.
Сравним: модель функциональной связи:
Разные разделы математической статистики посвящены обработке случайных величин в соответствии с разными задачами, например, с точки зрения расчета параметров выборки, или — отличия выборочных параметров от параметров генеральной совокупности, и т.д. Регрессионный анализ (РА) является тоже разделом математической статистики и в нем обрабатываются случайные величины со своих позиций, а именно:
регрессионный анализ устанавливает формы зависимости между этими величинами X и Y. Такая зависимость определяется некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров (красные линии на рис.5).
| Рис.5 |
| x |
| Y |
| x |
| Y |
| x |
| Y |
| а |
| б |
| в |
Наиболее общая задача РА: для экспериментальных данных, имеющих между собой стохастическую зависимость, подобрать наиболее адекватную математическую модель в виде уравнения регрессии, графически являющейся некоторой линией.
Отметим, что при изучении стохастических зависимостей кроме РА используют и корреляционный анализ.
Фразу «наиболее адекватную математическую модель» нужно понимать в соответствии со следующими положениями.
Для каждого конкретного значения xi, кроме зафиксированного значения yi величины Y, имеется также несколько других значений величины Y (в силу ее случайности): yi1, yi2, yi3,… yin, поэтому можно говорить о среднем значении:
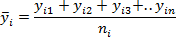 | (5) |
В итоге для каждого xi имеется свое значение 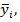
| x1 | x2 | x3 | … | xn |
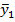 | 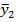 | 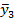 | … | 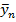 |
Если величина x не является случайной (через строчную букву обозначаются именно неслучайные величины), то зависимость по табл.2 является однозначной и искомой. В наиболее строгом варианте речь идет о некой генеральной совокупности, где между значениями Y и x имеется зависимость, а конкретно — зависимость между МО величины Y и величиной x, отражением которой является табл.2. Но дело в том, что эта зависимость имеет теоретическое значение, поскольку мы не знаем всей совокупности значений yi1, yi2, yi3,… yin, однако наиболее близкое к ней уравнение регрессии и будет наиболее адекватным.
Регрессия –это зависимость среднего значения (точнее – математического ожидания) случайной величины Y от величины x.
В РА рассматривается и вариант, когда величина X является случайной (через заглавные буквы обозначаются случайные величины), тогда речь будет идти о зависимости среднего значения случайной величины Y от среднего значения величины X (мое –проверить).
РА состоит из нескольких этапов:
§ выбор уравнения регрессии (математической модели);
§ оценка неизвестных параметров этой модели;
§ определяются статистические ошибки оценки или границы доверительных интервалов;
§ проверяется адекватность принятой математической модели экспериментальным данным.
- 2. Математическое описание систем автоматического управления
- 2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
- 2.2. Линеаризация уравнений динамики САУ (САР)
- Пример
- 2.3. Классический способ решения уравнений динамики
- Пример
- Линеаризация с помощью ряда Тейлора
- 📹 Видео
Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

2. Математическое описание систем автоматического управления
Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.
На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).
При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.
Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др
Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).
где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.
В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.
Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:
где, m — масса тела, Fj — все силы воздействующие на тело (поршень демпфера)
Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:
где — сила тяжести;
— сила сопротивления пружины,
— сила вязконо трения (пропорциональна скорости поршеня)
Размерности сил и коэффициентов, входящих в уравнение (2.1.2):
Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть
перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:
если , то уравнение принимает вид:
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).
Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:
тогда, разделив на k, имеем:
Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!
«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:
Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [
].
Тогда уравнение (2.1.6) можно записать в операторной форме:
, что эквивалентно
где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную
.
Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.
Введем новые нормированные (безразмерные) переменные:
Подставляя эти соотношения в уравнение (2.1.2), имеем:
Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на
, получаем:
где: — коэффициент усиления, причем безразмерный.
Проверим размерность коэффициента
Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.
На рис. 2.1.4 представлены статические характеристики для механического демпфера:
Процедура нормировки отклонений позволяет привести уравнения динамики к виду:
где дифференциальные операторы.
Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).
А если – нелинейные дифференциальные операторы, или
, то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).
Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»
Видео:Формула Тейлора за 3 минуты - bezbotvyСкачать

2.2. Линеаризация уравнений динамики САУ (САР)
Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:
- Нелинейностью статической характеристики.
- Нелинейностью динамических членов в уравнениях динамики.
- Наличием в САУ принципиально нелинейных звеньев.
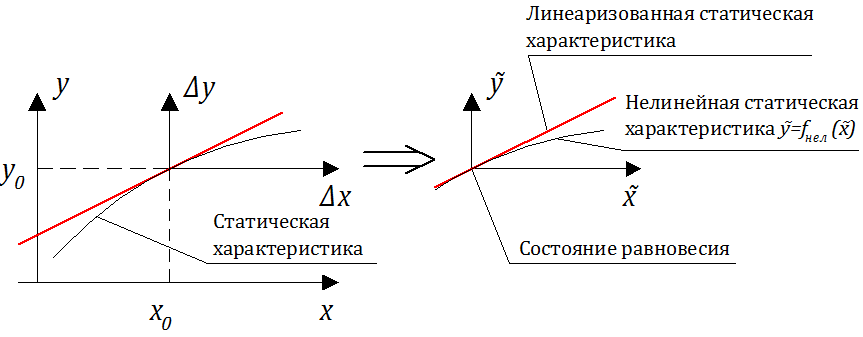
Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).
Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N0 Рис. 2.2.1 – Пример изменения мощности реактора
Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:
Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:
Перенесем в левую часть уравнения и запишем уравнение в виде%
где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.
Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .
Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки
будет выглядеть так:
C учетом вышеприведенного разложение принимает вид:
Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку
, получаем:
Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:
Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.
В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:
где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора
выше порядка оператора
:
Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.
Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).
Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:
Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>
Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на
, то уравнение принимает вид:
или в операторном виде:
Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.
Пример
Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x0, y0), если полное уравнение динамики имеет вид:
Нелинейность полного уравнения динамики проявляется в следующем:
• во-первых, в нелинейности статической характеристики:
• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.
Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x0, y0) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.
Преобразования выполним в следующей последовательности:
- Перейдем к безразмерным переменным (нормализованным);
- Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.
Перейдем к новым безразмерным переменным:
Заметим, что: .
Подставляя значения x(t) и y(t) в исходное уравнение:
Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости:
, получаем следующее уравнение:
Вводим новые обозначения:
Получаем уравнения в «почти» классическом виде:
Если в правой части вынести за общую скобку и разделить все уравнение на
, то уравнение (линеаризованное) принимает вид:
Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).
Видео:Частное решение ДУ, с помощью рядаСкачать

2.3. Классический способ решения уравнений динамики
Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.
Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:
Переходя к полной символике, имеем:
Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.
Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).
Требуется найти y(t) при известных начальных условиях.
где: — решение однородного дифференциального уравнения
y_(t) $inline$ — частное решение. $inline$
Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).
Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием
, поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:
Напомним этапы решения:
1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:
2) Записываем характеристическое уравнение:
3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:
если среди нет повторяющихся корней (кратность корней равна 1).
Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:
Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:
5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…
Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .
6) Суммируя полученные составляющие (собственную и вынужденную), имеем:
7) Используя начальные условия (t = 0), находим значения постоянных интегрирования .
Обычно получается система алгебраических уравнений.
Решая систему, находим значения постоянных интегрирования
Пример
Найти аналитическое выражение переходного процесса на выходе звена, если
Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем:
тогда:
где — неизвестные (пока) постоянные интегрирования.
По виду временной функции в правой части запишем как:
Подставляя в исходное уравнение, имеем:
Суммируя , имеем:
Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:
Решая систему уравнений относительно и
, имеем:
Тогда окончательно:
Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:
Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).
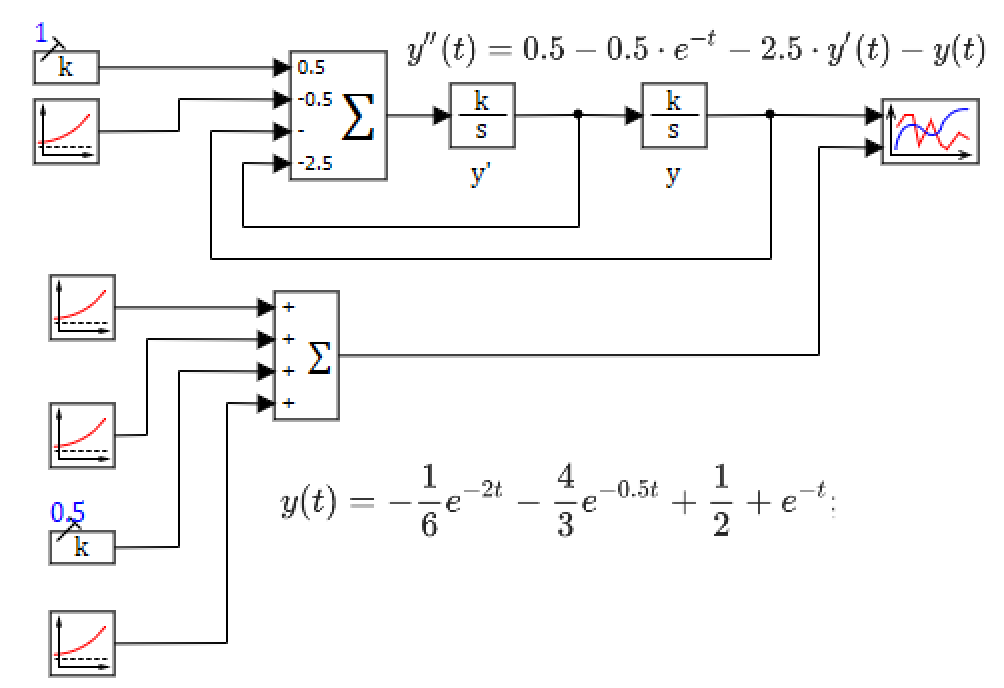
Рис. 2.3.1 – структурная схема для проверки решения
На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).
Видео:3) ТАУ для чайников. Часть 2.2: Математические модели...Скачать

Линеаризация с помощью ряда Тейлора
В этом случае функция y(x) раскладывается в ряд Тейлора в окрестности точки a (рис.6.1,б):
с отбрасыванием всех членов высшего порядка малости (в этом и состоит линеаризация):  , (2) , (2) |
где 
Второе слагаемое в (2) – дифференциал функции y(x) в точке a.
Пример.Исходная математическая модель является квадратным трехчленом:

Необходимо линеаризовать эту модель в окрестности точки x=2.
Решение. По (3) находим: 



Сравним результаты расчетов по формулам (3) и (4):
| x |  |  | Относительная погрешность,% |
| 2.01 | 4,03 | 4,03 | |
| 2,04 | 4,123 | 4,12 | 0,07 |
| 2,1 | 4,32 | 4,3 | 0,46 |
| 2,5 | 5,5 | 8,3 |
Как видим, при малых отклонениях погрешности получаются незначительными.
К тому же, модель (4) проще, чем (3), но недостатком такого подхода является необходимость пересчета коэффициентов (фактически построение другой модели) при существенном изменении значения x (например, при x=3).
📹 Видео
Теория автоматического управления. Лекция 5. Гармоническая линеаризацияСкачать

Задача на формулу Тейлора - bezbotvyСкачать

Атмосфера #10 | Линеаризация уравнений и уравнения для АГВСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Система уравнений. Метод алгебраического сложенияСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Составление и линеаризация дифференциального уравнения центробежного маятникаСкачать

Математический анализ, 39 урок, Формулы и ряды Тейлора и МаклоренаСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Решение систем уравнений методом подстановкиСкачать

Алгоритмы. Линеаризация функцийСкачать