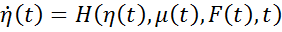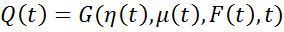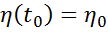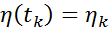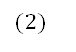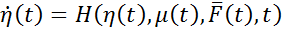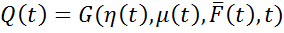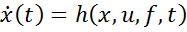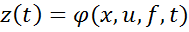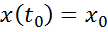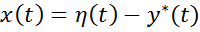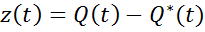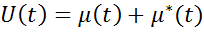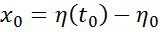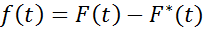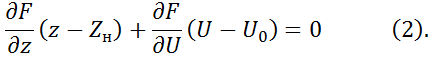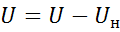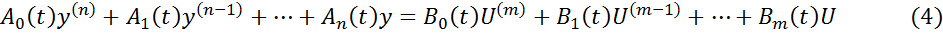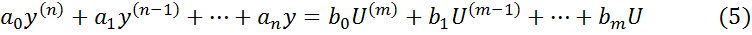Линеаризация дифференциальных уравнений управляемой системы вблизи программных траекторий

Страницы работы

Содержание работы

Статические характеристики исполнительных устройств, как правило, не линейные. Примеры:

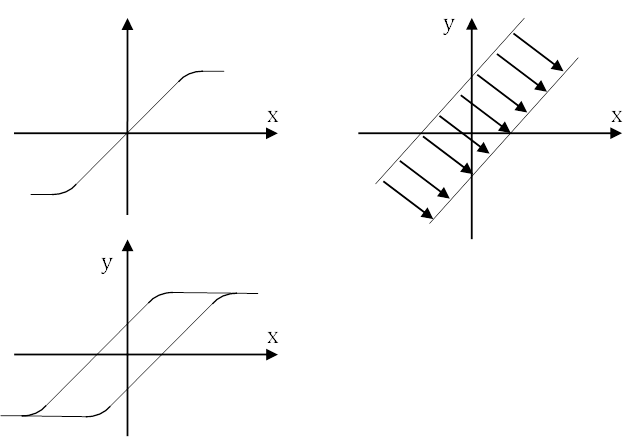Некоторые усилители мощности имеют гистерезисную статическую характеристику. Подобные характеристики могут принадлежать не только исполнительным устройствам, но и другим элементам системы управления.

Задачи автоматического управления.

Среди многообразия задач управления можно выразить 3 основных: задачи программного управления, стабилизации и слежения.

Задачи программного управления.

В этих задачах используются полные математические модели объектов управления, которые могут задаваться уравнениями состояний.

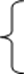
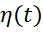
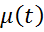
где — вектор состояния объекта (капа?); — вектор управляющих входов; F(t) – вектор возмущающих входов; Q(t) – вектор регулируемых выходов.

Пусть заданы начальные и конечные условия состояния объекта, которые выражают требования к качеству управления и отражают возможные ограничения на траекторию движения системы.

начальные условия:

конечные условия:

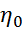
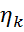
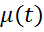
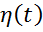
Задача программного управления заключается в нахождении такого управляющего воздействия μ(t), которое переводило бы объект из заданного начального состояния в заданное конечное , так, чтобы выполнялись требуемые условия на управление и траекторию движения. В этом случае управление будет называться программным управлением, а соответствующая ему траектория будет называться программной траекторией.

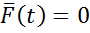
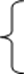
В системе уравнений (1) отмечены внешние возмущения F(t). Как правило, возмущения изменяются непредсказуемо, поэтому в программном управлении определяют некоторое среднее или номинальное значение F(t). Причем очень часто это значение задают , тогда можно записать уравнение в другом виде:

Система уравнений (2) будет называться системой невозмущенного движения, соответственно решение системы уравнений (2) будет также называться системой невозмущенного движения.

При описании объекта управления используют полную математическую модель объекта уравнения (1). Суть задачи состоит в следующем: требуется определить уравнение и параметры регулятора, работающего по принципу обратной связи, так чтобы выходные переменные Q(t) отслеживали задающее воздействие q(t).

Главным требованием в задаче слежения является требование устойчивости системы.

(3)

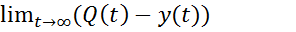
Другими требованиями могут быть – точность слежения, быстродействие, грубость и так далее.

Основным отличаем от задач стабилизации и задач программного управления является то, что задающие воздействия q(t) заранее неизвестны, и могут меняться непредвиденным образом, часто это случайные вектор-функции о которых известно лишь их поведение в статическом смысле (в конкретный момент времени). Поэтому, невозможно сформировать программное управление чтобы обеспечить движение объекта по заданной траектории. При рассмотрении задач слежения используют полные уравнения объекта.

Точно реализовать требуемое движение каппа от т и Q(t) практически невозможно. Причинами являются – неточное задание начальных условий, неточная реализация программных управлений, влияние внешних возмущений, отличных от нуля. В результате истинное движение объекта будет отличаться от программного, такие задачи решают задачи стабилизации. Для описания объекта в этом случае используют уравнения, описывающие отклонения истинного движения от программного. Эти уравнения называются уравнениями возмущенного движения.

— векторы отклонения действительного движения от заданного значения (*) – действительное остальное заданное движение; – вектор отклонения воздействия;

— начальное отклонение переменных состояния объекта; — изменение внешних возмущений.

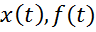
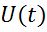
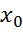
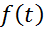
В задачах программного управления требуемое управление является функцией времени. В задачах же стабилизации требуется определить добавки в программном управлении так, чтобы заставить объект под действием полного управления двигаться по программной траектории или вблизи от нее.

Поскольку, начальные отклонения и изменения внешних возмущений обычно неизвестны, то управление ищется не как функция времени, а как функция изменяемых переменных (данные с датчиков), которые содержат информацию об отклонении. То есть, в задачах стабилизации требуется определить уравнения и параметры регулятора, работающего по принципу обратной связи.

Основным требованием является условие: 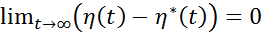– это условие асимптотической устойчивости системы.

Линеаризация уравнений и звеньев систем автоматического управления.

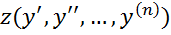
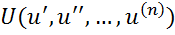
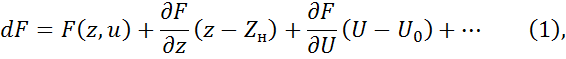
Линеаризация заключается в переходе к линейному дифференциальному равнению, переменные которого являются отклонениями от некоторого номинального режима. и (примем возмущение f = 0), описывают траекторию движения системы, если запишем уравнение движения системы:

так как уравнение с частными производными это нелинейное уравнение, т.е. частный случай решения.

Отбросим малые члены уравнения (1):

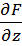
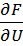
Уравнение (2) является приближенно линеаризованным уравнением, в этом уравнении и являются коэффициентами ряда Тейлора.

Введем новые переменные: отклонение от номинального

Так как все частные производные представляют из себя либо постоянные матрицы, либо матрицы, зависящие только от времени, то уравнение (2) с учетом допущений (3) есть либо система линейных дифференциальных уравнений с постоянными коэффициентами, относительно отклонений (3), либо система с переменными коэффициентами. Постоянство или переменность коэффициентов зависит от номинальной траектории. Например, в системах стабилизации, где номинальные траектории константы, получают постоянные матрицы. Таким образом, переходя к уравнениям в отклонениях, получаем системы линейных дифференциальных уравнений, которую будем рассматривать относительно выходной величины. Порядок этой системы равен порядку производной по y. Дифференцирование же входного сигнала рассматривается не как дифференциальное уравнение относительно сигнала u, а как операция с известным входным сигналом. То есть получаем дифференциальное уравнение вида:

A₀(t), A₁(t), … ,A_n(t) и B₀(t), B₁(t), … , B_n(t) – матрицы, которые описывают номинальную траекторию движения системы.

При удачной номинальной траектории матрицы А и В становятся постоянными, и для такой системы дифференциальных уравнений с постоянными коэффициентами можно получить до конца точное решение и полностью его исследовать. В случае постоянных коэффициентов система называется стационарной. Чаще всего входные и выходные величины это скалярные функции, то есть в системе имеется лишь по одному входу и одному выходу (одномерные системы), тогда матрицы превращаются в числа. Перепишем уравнение:

Переход от дифференциального уравнения n-ного порядка к системе из n-дифференциальных уравнений 1-го порядка.

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

2. Математическое описание систем автоматического управления

Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях

При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.

На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).

При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.

Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др

Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).

где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.

В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:

где, m — масса тела, F_j — все силы воздействующие на тело (поршень демпфера)

Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:

где — сила тяжести; — сила сопротивления пружины, — сила вязконо трения (пропорциональна скорости поршеня)

Размерности сил и коэффициентов, входящих в уравнение (2.1.2):

Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть

перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:

если , то уравнение принимает вид:

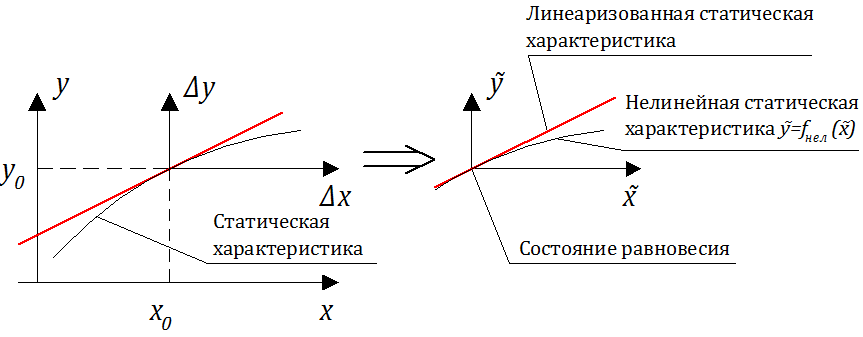
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).

Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:

тогда, разделив на k, имеем:

Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!

«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:

Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [].
Тогда уравнение (2.1.6) можно записать в операторной форме:

, что эквивалентно

где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную .

Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.

Введем новые нормированные (безразмерные) переменные:

Подставляя эти соотношения в уравнение (2.1.2), имеем:

Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на , получаем:

где: — коэффициент усиления, причем безразмерный.

Проверим размерность коэффициента

Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.

На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Процедура нормировки отклонений позволяет привести уравнения динамики к виду:

где дифференциальные операторы.

Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).

А если – нелинейные дифференциальные операторы, или , то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).

Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

2.2. Линеаризация уравнений динамики САУ (САР)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:

1. Нелинейностью статической характеристики.
2. Нелинейностью динамических членов в уравнениях динамики.
3. Наличием в САУ принципиально нелинейных звеньев.

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N₀ Рис. 2.2.1 – Пример изменения мощности реактора

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:

Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

Перенесем в левую часть уравнения и запишем уравнение в виде%

где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:

Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .

Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки будет выглядеть так:

C учетом вышеприведенного разложение принимает вид:

Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку , получаем:

Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:

Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.

В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:

где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора выше порядка оператора :

Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>

Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на , то уравнение принимает вид:

или в операторном виде:

Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.

Пример

Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x₀, y₀), если полное уравнение динамики имеет вид:

Нелинейность полного уравнения динамики проявляется в следующем:

• во-первых, в нелинейности статической характеристики:

• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.

Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x₀, y₀) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

1. Перейдем к безразмерным переменным (нормализованным);
2. Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.

Перейдем к новым безразмерным переменным:

Заметим, что:
.

Подставляя значения x(t) и y(t) в исходное уравнение:

Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости: , получаем следующее уравнение:

Вводим новые обозначения:

Получаем уравнения в «почти» классическом виде:

Если в правой части вынести за общую скобку и разделить все уравнение на , то уравнение (линеаризованное) принимает вид:

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

2.3. Классический способ решения уравнений динамики

Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.

Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:

Переходя к полной символике, имеем:

Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.

Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).

Требуется найти y(t) при известных начальных условиях.

где: — решение однородного дифференциального уравнения y_(t) $inline$ — частное решение. $inline$

Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).

Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием , поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:

Напомним этапы решения:

1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:

2) Записываем характеристическое уравнение:

3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:

если среди нет повторяющихся корней (кратность корней равна 1).

Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:

Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:

5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…

Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .

6) Суммируя полученные составляющие (собственную и вынужденную), имеем:

7) Используя начальные условия (t = 0), находим значения постоянных интегрирования . Обычно получается система алгебраических уравнений. Решая систему, находим значения постоянных интегрирования

Пример

Найти аналитическое выражение переходного процесса на выходе звена, если

Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем: тогда:

где — неизвестные (пока) постоянные интегрирования.

По виду временной функции в правой части запишем как:

Подставляя в исходное уравнение, имеем:

Суммируя , имеем:

Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:

Решая систему уравнений относительно и , имеем:
Тогда окончательно:

Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:

Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

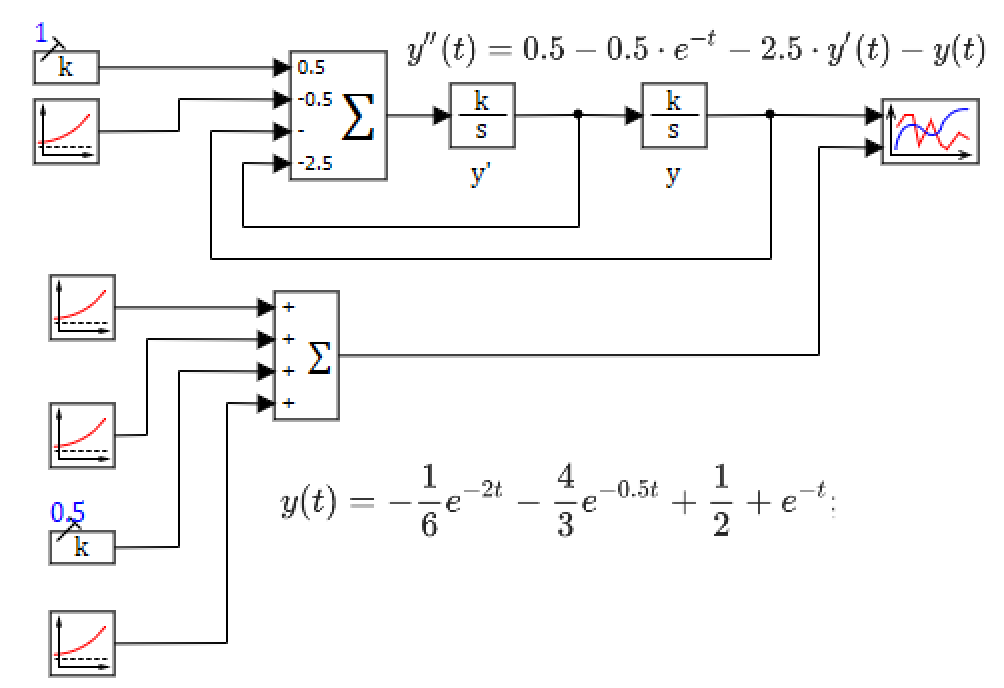
Рис. 2.3.1 – структурная схема для проверки решения

На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Линеаризация дифференциальных уравнений

Подавляющее большинство реальных элементов имеют нелинейные характеристики и, следовательно, описываются нелинейными дифференциальными уравнениями. Однако, многие нелинейные элементы можно линеаризовать, то есть заменить нелинейные уравнения элемента приближенными линейными. Это позволяет для анализа и синтеза систем управления использовать методы теории линейных систем, которые наиболее просты и хорошо разработаны. В основе линеаризации нелинейных уравнений лежит предположение, что в исследуемом динамическом процессе переменные координаты системы изменяются таким образом, что их отклонения от установившихся значений остаются все время достаточно малыми величинами. Это условие выполняется для замкнутых систем, так как последние работают по принципу ликвидации ошибки.

Геометрическая трактовка линеаризации. Изобразим графически нелинейную зависимость (рис. 2.1)

Рис. 2.1. Геометрическая интерпретация линеаризации

Текущие значения координат y и x запишем как

где y₀, x₀ – установившиеся значения, Dy, Dx – их отклонения от установившихся значений.

В рабочей точке ( x₀, y₀), определяемой установившимися значениями, заменим участок кривой касательной и получим прямую, описываемую линейным уравнением

где y_{н —} постоянная величина;

— коэффициент, определяемый наклоном касательной к кривой в рабочей точке ( x₀, y₀).

Для исключения из уравнения величины y_н перенесем начало координат в рабочую точку. Тогда получим линейное уравнение, связывающее между собой отклонения переменных величин от своих установившихся значений, вида

Таким образом, линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой на касательную к ней прямую в точке установившегося режима. Очевидно, что эта замена тем точнее, чем меньше величины отклонений координат элемента от своих установившихся значений в исследуемом динамическом процессе.

В общем случае при составлении уравнения динамики элемента системы (рис. 2.2), имеющего входную величину x, выходную — y и внешнее воздействие f, получается динамическое уравнение произвольного нелинейного вида

(2.3)

Рис. 2.2. Элемент автоматической системы

Допустим, что установившиеся значения переменных y, x и f являются постоянными величинами y₀, x₀, f₀, характеризующими установившийся режим и определяющими рабочую точку элемента.

Тогда для текущих координат можно записать

где Dy, Dx, Df – отклонения y, x, f от своих установившихся значений.

Из (2.3) получается уравнение статики

Для линеаризации уравнения (2.3) последнее раскладывают в ряд Тейлора по степеням отклонений всех координат элемента от своих установившихся значений. Тогда уравнение (2.3) примет вид

+ (члены высшего порядка малости). (2.5)

Вычитая из последнего уравнения (2.5) уравнение статики (2.4) и отбросив все последующие члены разложения как малые высшего порядка, придем к линейному уравнению динамики элемента

(2.6)

Здесь нижний индекс “0” обозначает, что значения частных производных должны быть определены в точке установившегося режима элемента.

Это дифференциальное уравнение, так же как и (2.3), описывает тот же динамический процесс в том же элементе автоматической системы. Сравним (2.3) и (2.6):

уравнение (2.3) — точное, а уравнение (2.6) — приближенное, ибо в процессе его получения были отброшены малые высшего порядка;

уравнение (2.3) записано относительно переменных величин элемента, а уравнение (2.6) — относительно отклонений переменных от своих установившихся значений;

уравнение (2.3) — нелинейное, уравнение (2.6) — линейное относительно отклонений, коэффициенты которого определяются рабочей точкой элемента, то есть его установившимися значениями; при смене рабочей точки эти коэффициенты изменяются.

Таким образом, цель получения линейного дифференциального уравнения взамен прежнего нелинейного достигнута. Уравнение (2.6) называется дифференциальным уравнением элемента в отклонениях.

Ограничение метода. Данным методом могут быть линеаризованы уравнения элементов, статические характеристики которых в окрестности точки установившегося режима гладкие, то есть их производные непрерывны и однозначны. Не могут быть линеаризованы уравнения элементов с негладкими, неоднозначными и имеющими разрывы в окрестности точки установившегося режима статическими характеристиками.

Замечание: в дальнейшем будем использовать только линеаризованные уравнения, записанные относительно отклонений от установившихся значений переменных, однако для сокращения записи знак “D” будем опускать.

Пример. Электромагнитный момент M электродвигателя постоянного тока с независимым возбуждением определяется нелинейным уравнением

где c — постоянный коэффициент;

Iя, Iв — токи, протекающие в цепях якоря и возбуждения.

Решение. Линеаризуем выражение для M разложением в ряд Тэйлора и учетом лишь линейных составляющих ряда. В результате получим соотношение для малых приращений

Здесь нижним индексом “0” обозначены установившиеся значения переменных, относительно которых изменяются их приращения.

🔍 Видео

Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Составление и линеаризация дифференциального уравнения центробежного маятникаСкачать

Давай подиффуримся! Ортогональные и изогональные траекторииСкачать

ОДУ. 4 Системы дифференциальных уравненийСкачать

Поле направлений дифференциального уравнения первого порядкаСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

3) ТАУ для чайников. Часть 2.2: Математические модели...Скачать